Shanghai University
Article Information
- T. HAYAT, T. HUSSAIN, S. A. SHEHZAD, A. ALSAEDI. 2015.
- Flow of Oldroyd-B fluid with nanoparticles and thermal radiation
- Appl. Math. Mech. -Engl. Ed., 36(1): 69-80
- http://dx.doi.org/10.1007/s10483-015-1896-9
Article History
- Received 2014-1-12;
- in final form 2014-6-18
2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia;
3. Department of Mathematics, Faculty of Computing, Mohammad Ali Jinnah University, Islamabad 44000, Pakistan;
4. Department of Mathematics, COMSATS Institute of Information Technology, Sahiwal 57000, Pakistan
A working fluid is involved in many engineering and industrial processes which is used to transfer energy/heat from one position to another position. The enhancement in energy transfer has been a serious issue for a long time. Nanofluid is a better candidate in this regard. Ad- vancement in nanoparticles is acting as a new heat transfer medium which introduced new and high potentials. The common working fluids involved in industry and engineering processes have less thermal conductivity in comparison to metal and metal oxides. An enhancement in heat transfer performance can be obtained by adding high conductivity materials in base fluids[1, 2]. The betterment in the performance of thermal conductivity without causing a pres- sure drop is the major advantage of nanofluids. As a consequence,the performance of various heat transfer devices is increased,which leads to the larger capacity of operating systems. Such fluids are looking to be very interesting in transportation,nuclear reactors,solar collectors, car radiators,chillers,micro-electro mechanical systems,cooling of electronic devices,and in cooling/heating of energy conversion. Having such in view,Oztop and Abu-Nada[3] discussed the buoyancy driven flow of nanofluid filled in an enclosure. A numerical solution was pre- sented. Turkyilmazoglu[4] presented a study to analyze the magnetohydrodynamic (MHD) flow of nanofluid with heat and mass transfer in the presence of thermal slip boundary condition. Both exact and analytical solutions were given. The boundary flow of nanofluid over a verti- cal plate with convective thermal condition was examined by Rashidi et al.[5]. They used the differential transform method to obtain the results of the velocity,the temperature,and the vol- umetric fraction of nanoparticles. The effect of double-stratification was numerically analyzed on the boundary layer flow of nanofluid over a vertical flat plate by Ibrahim and Makinde[6]. Moradi et al.[7] studied the Jeffery-Hamel flow of nanofluid with viscous dissipation. Hatami and Ganji[8] carried out an analysis to examine the sodium alginate (SA) TiO2 non-Newtonian nanofluid passing through a porous medium between two coaxial cylinders. Sheikholeslami et al.[9] investigated the flow of nanofluid in a semi-porous channel. They computed the solution expressions using the least square and Galerkin methods. The effects of the buoyancy force, convective heating,the Brownian motion,and thermophoresis in the MHD stagnation point flow of nanofluid were examined by Makinde et al.[10]. They obtained the numerical solution by the Runge-Kutta fourth-order scheme.
The boundary layer flow of non-Newtonian fluid over a surface has attained considerable attention from the recent investigators due to its broad applications in the industrial and engi- neering processes. More specifically,the flow and heat transfer of non-Newtonian fluids have key importance in power engineering,petroleum production,polymer solutions,paper production, etc. The fluid model under consideration is an Oldroyd-B fluid,which falls into the category of rate type non-Newtonian fluid. It exhibits the characteristics of the relaxation time and the retardation time. Very little has been said yet about the boundary layer flow of the Oldroyd-B fluid. Sajid et al.[11] initiated the boundary layer stagnation point flow of an Oldroyd-B fluid towards a stretching surface. They presented the results numerically. Hayat et al.[12] extended this analysis for the three-dimensional flow of an Oldroyd-B fluid with a convective boundary condition. The three-dimensional flow of an Oldroyd-B fluid with variable thermal conductiv- ity and heat generation/absorption was recently addressed by Shehzad et al.[13]. Moreover,the importance of thermal radiation is prevalent in the industrial and space technological processes at very high temperature. Examples of such processes are glass production and furnace design, comical flight aerodynamic rocket,space craft re-entry,plasma physics,propulsion systems,etc. Further,the heat generation/absorption plays a vital role in disassociating fluids in packed-bed reactors,storage of food stuffs,and heat removal from nuclear fuel debris,underground disposal of radioactive waste material,and many others[14, 15, 16, 17, 18].
The present investigation deals with the two-dimensional boundary layer flow of an Oldroyd- B fluid with nanoparticles. Mathematical formulation consists of convective heat and mass con- ditions. Besides these,the contributions due to thermal radiation and heat generation/absorpt- ion are also taken into account. The governing nonlinear problems are computed for the se- ries solutions through the homotopy analysis method (HAM)[19, 20, 21, 22, 23, 24, 25]. Discussion reflecting the interpretation of sundry parameters is made. Important conclusions are presented. 2 Mathematical formulation
An incompressible flow of an Oldroyd-B nanofluid over a stretching sheet is considered. The fluid is assumed to be incompressible. We assume that the surface heated by a hot fluid has the temperature Tf and the concentration Cf . The heat and mass transfer coefficients are denoted by h1 and h2,respectively. The effects of the Brownian motion and thermophoresis are presen- ted. We also consider heat and mass transfer in the presence of thermal radiation and heat gen- eration. The governing boundary layer equations for the present problem are given as follows:
The boundary conditions for the considered flow analysis are where u and v are the velocity components in the x- and y-directions,v is the kinematic viscosity, λ1 and λ2 are the relaxation time and the retardation time,respectively,ρf is the density of fluid,α is the thermal diffusivity,τ (= (ρc)p/(ρc)f ) is the ratio of the nanoparticle heat capacity and the base fluid heat capacity,qr is the radiative heat flux,Q is the heat source/sink parameter, DB is the Brownian diffusion coefficient,DT is the thermophoretic diffusion coefficient,k is the thermal conductivity,uw is the stretching velocity at the wall,and T∞ and C∞ are the ambient temperature and the concentration,respectively. The radiative heat flux qr using Rosseland’s approximation gives in which σ is the Stefan-Boltzmann constant,and k* is the mean absorption coefficient. The temperature difference within the flow is assumed in such a manner that T4 can be written in the linear combination of temperature. By expanding T4 about T∞ in terms of Taylor’s series and neglecting higher order terms,we have and Now,Eq. (3) reduces to Use the following transformations: Then,Eqs. (2),(4)-(6),and (10) become where β1 = λ1c is the Deborah number with respect to the relaxation time,β2 = λ2c is the Deborah number with respect to the retardation time,Pr = v/α is the Prandtl number,Tr = 4σT∞3 /(kk*) is the radiation parameter,Sc = v/DB is the Schmidt number,Nb = (ρc)pDB(Cf− C∞)/((ρc)fv) is the Brownian motion parameter,Nt = (ρc)pDT(Tf − T∞)/((ρc)fvT∞) is the thermophoresis parameter,and Bi1 (= (h1/k)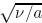 ) and Bi2 (= (h2/DB)
) and Bi2 (= (h2/DB) 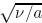 ) are the Biot
numbers. The local Nusselt number and the local Sherwood number are given by
where qw is the surface heat flux,and qm is the surface mass flux. The local Nusselt and local
Sherwood numbers in dimensionless forms are given below:
where Rex = uw(x)x/v is the local Reynolds number.
3 Homotopy analysis solutions
By choosing a set of base functions[19]
the functions f,θ,and φ can be expressed as follows:
in which am,nk,bm,nk,and cm,nk are the coefficients. The initial guesses and auxiliary linear
operators are selected in the following forms:
subject to the properties
where Ci (i = 1,2,· · · ,7) are the arbitrary constants. The zeroth order problems are defined
as follows[20, 21, 22, 23, 24, 25]:
where
) are the Biot
numbers. The local Nusselt number and the local Sherwood number are given by
where qw is the surface heat flux,and qm is the surface mass flux. The local Nusselt and local
Sherwood numbers in dimensionless forms are given below:
where Rex = uw(x)x/v is the local Reynolds number.
3 Homotopy analysis solutions
By choosing a set of base functions[19]
the functions f,θ,and φ can be expressed as follows:
in which am,nk,bm,nk,and cm,nk are the coefficients. The initial guesses and auxiliary linear
operators are selected in the following forms:
subject to the properties
where Ci (i = 1,2,· · · ,7) are the arbitrary constants. The zeroth order problems are defined
as follows[20, 21, 22, 23, 24, 25]:
where  f ,
f , θ,and
θ,and  φ are the non-zero auxiliary parameters,q 2 [0,1] is an embedding pa-
rameter,and Nf ,Nθ,and Nφ are the nonlinear operators. Putting q = 0 and q = 1,one
has
If we increase the value of q from 0 to 1,then f(η,q),θ(η,q),and φ(η,q) vary from f0(η),θ0(η),
and φ0(η) to f(η),θ(η),and φ(η). By adopting the Taylor series expansion,we have
The convergence of the above series highly depends upon the suitable values of
φ are the non-zero auxiliary parameters,q 2 [0,1] is an embedding pa-
rameter,and Nf ,Nθ,and Nφ are the nonlinear operators. Putting q = 0 and q = 1,one
has
If we increase the value of q from 0 to 1,then f(η,q),θ(η,q),and φ(η,q) vary from f0(η),θ0(η),
and φ0(η) to f(η),θ(η),and φ(η). By adopting the Taylor series expansion,we have
The convergence of the above series highly depends upon the suitable values of  f ,
f , θ,and
θ,and
 φ. Considering that
φ. Considering that  f ,
f , θ,and
θ,and  φ are selected properly such that Eqs. (34)-(36) converge at
The general solutions can be written as
where fm*,θm*,and φm*(η) are the special solutions.
4 Convergence of homtopy solutions and discussion
φ are selected properly such that Eqs. (34)-(36) converge at
The general solutions can be written as
where fm*,θm*,and φm*(η) are the special solutions.
4 Convergence of homtopy solutions and discussion
The auxiliary parameters  f,
f, θ,and
θ,and  φ are important in controlling and adjusting the
convergence region of series solutions. We plot the
φ are important in controlling and adjusting the
convergence region of series solutions. We plot the  -curves at the 22nd-order of HAM approxi-
mations in order to find the appropriate values. It is noted from Fig. 1 that the suitable values of
-curves at the 22nd-order of HAM approxi-
mations in order to find the appropriate values. It is noted from Fig. 1 that the suitable values of
 f,
f, θ,and
θ,and  φ are −1.45 6
φ are −1.45 6  f 6 −0.10,−1.25 6
f 6 −0.10,−1.25 6  θ 6 −0.50,and −1.20 6
θ 6 −0.50,and −1.20 6  φ 6 −0.30,respec-
tively. The series converge in the whole region of η when
φ 6 −0.30,respec-
tively. The series converge in the whole region of η when  f =
f = θ=
θ= φ =−0.8 (see Table 1).
φ =−0.8 (see Table 1).
 |
Fig. 1  -curves for functions f′′(0),θ′(0),and φ′(0) at 22nd-order of approximations when β1 = β2 =
0.3,S = 0.1,Pr = 1.0,Sc = 0.8,Nt = 0.2,Nb = 0.3,Bi1 = Bi2 = 0.8,and Tr = 0.4 -curves for functions f′′(0),θ′(0),and φ′(0) at 22nd-order of approximations when β1 = β2 =
0.3,S = 0.1,Pr = 1.0,Sc = 0.8,Nt = 0.2,Nb = 0.3,Bi1 = Bi2 = 0.8,and Tr = 0.4 |
 f =
f =  θ =
θ =
 φ = −0.8
φ = −0.8  |
We plot Figs. 2−9 to examine the behaviors of the Deborah numbers β1 and β2,the Prandtl number Pr,the Biot number Bi1,the thermophoresis and Brownian motion parameters Nt and Nb,the radiation parameter Tr,and the heat generation parameter S on the dimensionless temperature θ(η). The variations in the temperature θ(η) for different values of the Deborah number β1 are seen in Fig. 2. Here,one can see that the temperature is lower for smaller values of the Deborah number β1 and higher for larger values of the Deborah number. Since the Deborah number β1 is directly proportional to the relaxation time,an increase in the value of β1 corresponds to an increase in the relaxation time. Higher relaxation time gives rise to the temperature and the thermal boundary layer thickness. It is noted from Fig. 3 that the temper- ature and the thermal boundary layer thickness are reduced with an increase in the Deborah number β2. This is due to the fact that the Deborah number β2 is directly proportional to the retardation time. An increase in the retardation time corresponds to lower temperature and thinner thermal boundary layer. The comparison of Figs. 2 and 3 shows that the Deborah numbers β1 and β2 have reverse effects on the temperature. Figure 4 depicts that both the temperature and the thermal boundary layer thickness increase when the values of the Prandtl number are smaller. The Prandtl number is the ratio of momentum to thermal diffusivities. A reduction in the value of the Prandtl number implies higher thermal diffusivity and smaller mo- mentum diffusivity. Higher thermal diffusivity and lower momentum diffusivity are responsible for an increase in the temperature when the value of the Prandtl number decreases. Figure 5 illustrates that the temperature increases for larger Biot number Bi1. It is seen that beyond Bi1 = 0.8,the increase in the temperature slows down. An increase in the temperature corre- sponding to the Biot number Bi1 is due to the heat transfer coefficient h1. The definition of Bi1 involves the heat transfer coefficient h1. The heat transfer coefficient increases when the value of Bi1 increases. This increase in the heat transfer coefficient leads to an enhancement in the temperature and the thermal boundary layer thickness. Variations in temperature vs. η for different values of the thermophoresis and Brownian motion parameters are examined in Figs. 6 and 7. These figures show that the temperature is enhanced for larger values of the thermophoresis and Brownian motion parameters. Also,we notice that the variations in the temperature due to the thermophoresis parameter are much more than the variations due to the Brownian motion parameter. An increase in the radiation parameter leads to an increase in the temperature and the thermal boundary layer thickness (see Fig. 8). In fact,the increase in the radiation parameter leads to an enhancement in the fluid temperature. Figure 9 illustrates the variations in the temperature for various values of the heat generation parameter S. It is found that the temperature and the thermal boundary layer thickness are increasing functions of the heat generation parameter.
 |
| Fig. 2 Influence of β1 on temperature θ(η) vs. η when β2 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nt = Nb=0.2,Tr = 0.4,and S= 0.2 |
 |
| Fig. 3 Influence of β2 on temperature θ(η) vs. η when β1 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nt = Nb=0.2,Tr = 0.5,and S= 0.2 |
 |
| Fig. 4 Influence of Pr on temperature θ(η) vs. η when β1 =β2 = 0.4,Sc =1.0 ,Bi1 = Bi2 = 0.8,Nt = Nb=0.2,Tr = 0.5,and S= 0.2 |
 |
| Fig. 5 Influence of Bi1 on temperature θ(η) vs. η when β1 =β2 = 0.4,Pr = Sc =1.0 ,Bi2 = 0.8,Nt = Nb=0.2,Tr = 0.5,and S= 0.2 |
 |
| Fig. 6 Influence of Nt on temperature θ(η) vs. η when β1 =β2 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nb=0.2,Tr = 0.5,and S= 0.2 |
 |
| Fig. 7 Influence of Nb on temperature θ(η) vs. η when β1 =β2 = 0.4,Nt = 0.2,Tr = 0.5,and S= 0.2 |
 |
| Fig. 8 Influence of Tr on temperature θ(η) vs. η when β1 =β2 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nt = Nb=0.2,and S= 0.2 |
 |
| Fig. 9 Influence of S on temperature θ(η) vs. η when β1 =β2 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nt = Nb=0.2,Tr = 0.5 |
To see the variations in the concentration φ(η) for different values of the Deborah numbers β1 and β2,the Schmidt number Sc,the Biot number Bi2,the thermophoresis parameter Nt, and the Brownian motion parameter Nb,Figs. 10-15 are presented. Figures 10 and 11 elu- cidate that the Deborah numbers β1 and β2 have reverse effects on the concentration φ(η). The concentration φ(η) increases for higher values of β1,while it reduces for larger values of β2. Also,it is analyzed that the influence of β1 and β2 on the temperature θ(η) and the con-centration φ(η) is qualitatively similar. It is noticed from Fig. 12 that the concentration φ(η) and its related boundary layer thickness are lower for higher values of the Schmidt number. The Schmidt number is dependent on the Brownian diffusion coefficient. An increase in the Schmidt number implies a reduction in the Brownian diffusion coefficient. Such a decrease in the Brownian diffusion coefficient causes a reduction in the concentration φ(η). The change in the concentration φ(η) for different values of the Biot number Bi2 is analyzed in Fig. 13. We can see that the concentration φ(η) increases when the value of Bi2 increases. The change in the concentration φ(η) is larger for smaller values of Bi2,while this change is smaller when we increase the value of Bi2 from 0.8 onward. Figure 13 is plotted to see the effects of the thermophoresis and Brownian motion parameters on the concentration φ(η). We examine that the thermophoresis and Brownian motion parameters have opposite effects on the concentra- tion φ(η). The concentration φ(η) increases with an increase in the thermophoresis parameter, but it decreases for higher values of the Brownian motion parameter. Also,we analyze that the decrease in the concentration φ(η) is rapid for Nb = 0.1,0.3,but it is very small when Nb = 0.5,0.7,1.0.
 |
| Fig. 10 Influence of β1 on temperature θ(η) vs. η when β2 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nt = Nb=0.2,Tr=0.5,and S= 0.2 |
 |
| Fig. 11 Influence of β2 on temperature θ(η) vs. η when β1 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nt = Nb=0.2,Tr=0.5,and S= 0.2 |
 |
| Fig. 12 Influence of Sc on temperature θ(η) vs. η when β1 =β2 = 0.4,Pr =1.0 ,Bi1 = Bi2 = 0.8,Nt = Nb=0.2,Tr=0.5,and S= 0.2 |
 |
| Fig. 13 Influence of Bi2 on temperature θ(η) vs. η when β1 =β2 = 0.4,Pr = Sc =1.0 ,Bi1 = 0.8,Nt = Nb=0.2,Tr=0.5,and S= 0.2 |
 |
| Fig. 14 Influence of Nt on temperature θ(η) vs. η when β1 =β2 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nb=0.2,Tr=0.5,and S= 0.2 |
 |
| Fig. 15 Influence of Nb on temperature θ(η) vs. η when β1 =β2 = 0.4,Pr = Sc =1.0 ,Bi1 = Bi2 = 0.8,Nt=0.2,Tr=0.5,and S= 0.2 |
Table 1 is computed to see the convergent values of −f′′(0),−θ′(0),and −φ′(0) at different orders of HAM approximations. It is seen that the value of −f′′(0) converges from the 10th- order of approximations,while it converges from 35th-order of deformations for −θ′(0) and −φ′(0). It is concluded from the tabular values that 35th-order deformations are sufficient for the convergent solutions. Table 2 is computed to examine the numerical values of the local Nusselt and Sherwood numbers for various values of Nt,Nb,Tr,Pr,Bi1,and Bi2 when β1 = β2 = S = 0.1. It is seen that the values of the local Nusselt and Sherwood numbers are reduced when the value of Nt increases. The value of the local Sherwood number increases by increasing the value of the Brownian motion parameter.
 |
We investigate the two-dimensional boundary layer flow of an Oldroyd-B nanofluid with convective heat and mass conditions. The analysis is carried out with thermal radiation and heat generation. This study has the following key observations:
(i) An increase in the value of β1 leads to an increase in the temperature θ(η) and the concentration φ(η),but a reverse behavior is noted for higher values of β2.
(ii) The temperature θ(η) and the concentration φ(η) are increasing functions of the Biot numbers Bi1 and Bi2.
(iii) Larger values of the thermophoresis and Brownian motion parameters give rise to the temperature θ(η).
(iv) The temperature θ(η) increases when we increase the value of the radiation parameter Tr.
(v) The temperature θ(η) is an increasing function of the heat generation parameter S.
(vi) The concentration φ(η) is reduced for higher values of the Schmidt number Sc.
(vii) The influence of the thermophoresis and Brownian motion on the concentration φ(η) is quite reverse.
Acknowledgements The authors acknowledge with thanks to the Deanship of Scientific Research (DSR) for technical and financial support.| [1] | Choi, S. U. S. Enhancing thermal conductivity of fluids with nanoparticles. The Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, ASME, San Francisco, 66, 99-105 (1995) |
| [2] | Ding, Y., Chen, H., Wang, L., Yang, C., He, Y., Yang, W., Lee, W. P., Zhang, L., and Huo, R. Heat transfer intensification using nanofluids. Kona, 25, 23-38 (2007) |
| [3] | Oztop, H. F. and Abu-Nada, E. Numerical study of natural convection in partially heated rectan-gular enclosures filled with nanofluids. International Journal of Heat and Fluid Flow, 29, 1326-1336 (2008) |
| [4] | Turkyilmazoglu, M. Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids. Chemical Engineering Science, 84, 182-187 (2012) |
| [5] | Rashidi, M. M., Beg, O. A., Asadi, M., and Rastegari, M. T. DTM-Padé modeling of natural convective boundary layer flow of a nanofluid past a vertical surface. International Journal of Thermal and Environmental Engineering, 4, 13-24 (2012) |
| [6] | Ibrahim, W. and Makinde, O. D. The effect of double stratification on boundary-layer flow and heat transfer of nanofluid over a vertical plate. Computers and Fluids, 86, 433-441 (2013) |
| [7] | Moradi, A., Alsaedi, A., and Hayat, T. Investigation of heat transfer and viscous dissipation effects on the Jeffery-Hamel flow of nanofluids. Thermal Science (2012) DOI 10.2298/TSCI120410208M |
| [8] | Hatami, M. and Ganji, D. D. Heat transfer and flow analysis for SA-TiO2 non-Newtonian nanofluid passing through the porous media between two coaxial cylinders. Journal of Molecular Liquids, 188, 155-161 (2013) |
| [9] | Sheikholeslami, M., Hatami, M., and Ganji, D. D. Analytical investigation of MHD nanofluid flow in a semi-porous channel. Powder Technology, 246, 327-336 (2013) |
| [10] | Makinde, O. D., Khan, W. A., and Khan, Z. H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Interna-tional Journal of Heat and Mass Transfer, 62, 526-533 (2013) |
| [11] | Sajid, M., Abbas, Z., Javed, T., and Ali, N. Boundary layer flow of an Oldroyd-B fluid in the region of a stagnation point over a stretching sheet. Canadian Journal of Physics, 88, 635-640 (2010) |
| [12] | Hayat, T., Shehzad, S. A., Alsaedi, A., and Alhothuali, M. S. Three-dimensional flow of Oldroyd-B fluid over surface with convective boundary conditions. Applied Mathematics and Mechanics (English Edition), 34(4), 489-500 (2013) DOI 10.1007/s10483-013-1685-9 |
| [13] | Shehzad, S. A., Alsaedi, A., Hayat, T., and Alhuthali, M. S. Three-dimensional flow of an Oldroyd-B fluid with variable thermal conductivity and heat generation/absorption. Plos One, 8 (2013) DOI 10.1371/journal.pone.0078240 |
| [14] | Turkyilmazoglu, M. Thermal radiation effects on the time-dependent MHD permeable flow having variable viscosity. International Journal of Thermal Sciences, 50, 88-96 (2011) |
| [15] | Olanrewaju, P. O., Gbadeyan, J. A., Hayat, T., and Hendi, A. A. Effects of internal heat gen-eration, thermal radiation and buoyancy force on a boundary layer over a vertical plate with a convective surface boundary condition. South African Journal of Sciences, 107, 80-85 (2011) |
| [16] | Bhattacharyya, K., Mukhopadhyay, S., Layek, G. C., and Pop, I. Effects of thermal radiation micropolar fluid flow and heat transfer over a porous shrinking sheet. International Journal of Heat and Mass Transfer, 55, 2945-2952 (2012) |
| [17] | Parsa, A. B., Rashidi, M. M., and Hayat, T. MHD boundary-layer flow over a stretching surface with internal heat generation or absorption. Heat Transfer鈥擜sian Research, 42, 500-514 (2013) |
| [18] | Shehzad, S. A., Alsaedi, A., and Hayat, T. Hydromagnetic steady flow of Maxwell fluid over a bidirectional stretching surface with prescribed surface temperature and prescribed surface heat flux. Plos One, 8 (2013) DOI 10.1371/jarnal.pone.0068139 |
| [19] | Liao, S. J. Homotopy Analysis Method in Nonlinear Differential Equations, Springer and Higher Education Press, Heidelberg (2012) |
| [20] | Turkyilmazoglu, M. Solution of the Thomas-Fermi equation with a convergent approach. Communications in Nonlinear Science and Numerical Simulation, 17, 4097-4103 (2012) |
| [21] | Hayat, T., Shehzad, S. A., and Alsaedi, A. Soret and Dufour effects in magnetohydrodynamic (MHD) flow of Casson fluid. Applied Mathematics and Mechanics (English Edition), 33(10), 1301-1312 (2012) DOI 10.1007/s10483-012-1623-6 |
| [22] | Shehzad, S. A., Alsaadi, F. E., Monaquel, S. J., and Hayat, T. Soret and Dufour effects on the stagnation point flow of Jeffery fluid with convective boundary conditions. The European Physical Journal Plus, 128 (2013) DOI 10.1140/epjp/i2013-120506-6 |
| [23] | Abbasbandy, S., Hashemi, M. S., and Hashim, I. On convergence of homotopy analysis method and its application to fractional integro-differential equations. Quaestiones Mathematicae, 36, 93-105 (2013) |
| [24] | Rashidi, M. M., Ali, M., Freidoonimehr, N., and Nazari, F. Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy, 55, 497-510 (2013) |
| [25] | Hayat, T., Shehzad, S. A., and Alsaedi, A. Three-dimensional stretched flow of Jeffery fluid with variable thermal conductivity and thermal radiation. Applied Mathematics and Mechanics (English Edition), 34(7), 823-832 (2013) DOI 10.1007/s10483-013-1710-7 |
 2015, Vol. 36
2015, Vol. 36























