Shanghai University
Article Information
- Da-ming LI, Xiao-yu LI, Yan-qing LI, R. J. FARAHANI. 2015.
- Flow pattern analysis of linear gradient flow distribution
- Appl. Math. Mech. -Engl. Ed., 36(1): 81-106
- http://dx.doi.org/10.1007/s10483-015-1920-9
Article History
- Received 2014-4-2;
- in final form 2014-9-19
2. Civil and Environmental Engineering, Johns Hopkins University, Baltimore 21218, U. S. A.;
3. Civil Engineering, The University of Adelaide, Adelaide 5005, Australia
In a fluid domain,flow parameters can vary with time and space. These variations can lead to streamline bending and pulsation,resulting in vortex formation and turbulence as shown in Fig. 1[1]. Reynolds’ experiments[2] revealed the transformation of flow regime from laminar to turbulent flow. Ludwig Plandtl[3] proposed the boundary-layer theory. Boundary layer is defined as a thin layer close to a wall surface where the velocity gradient is large. Flow is considered to be potential outside the boundary layer. The boundary layer theory defines the transition of flow regime from turbulent flow in the boundary layer to laminar flow outside the boundary layer. In this study,the emergence of vortices in a gradient flow distribution is investigated. In the previous studies,several theoretical investigations and experimental measurements have been conducted to define the vortex formation close to a wall surface (Mc-Quivey and Richardson[4],Esfahanian et al.[5],Li et al.[6],Summer and Akosile[7],Wang et al.[8],Huang and Zhou[9],Ehrenstein et al.[10],Gires et al.[11],K´ad´ar and Balan[12],and Ashrafi and Hazbavi[13]).
 |
| Fig. 1. Vortex formation by linear gradient flow distribution |
In this study,for the first time,differential equations are solved considering the inertia term along the flow direction. The Oseen transformation is used to decompose the differential equations,and the vorticity,velocity,and pressure solutions are obtained using a new contour integral method. Theoretical results can be used in a variety of problems related to vortex formation close to the wall surface. 2 Vorticity equation of linear gradient flow distribution
A linear gradient flow distribution close to a flat wall is studied as shown in Fig. 2. The
flow direction is along the x-direction. The maximum velocity at the upper boundary is given
as U. The velocity is expressed as u =  z = kz,where k =
z = kz,where k =  is the velocity gradient,and
h is the total depth. The time-averaged flow velocity is given as V = (kz,0,0). The vortex
flow velocity vector V is given as V = (u,v,w). The instantaneous flow velocity vector V ′
is given as V ′ = (u′,v′,w′),where V ′ = V + V . The vorticity in the y-direction is defined
as wy =
is the velocity gradient,and
h is the total depth. The time-averaged flow velocity is given as V = (kz,0,0). The vortex
flow velocity vector V is given as V = (u,v,w). The instantaneous flow velocity vector V ′
is given as V ′ = (u′,v′,w′),where V ′ = V + V . The vorticity in the y-direction is defined
as wy =  . The instantaneous flow satisfies the incompressible viscous equation of continuity and momentum. In the Cartesian coordinates,these equations are expressed by
. The instantaneous flow satisfies the incompressible viscous equation of continuity and momentum. In the Cartesian coordinates,these equations are expressed by
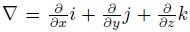 is the gradient operator,ρ is the fluid density,p′
is the instantaneous pressure,ν is the kinematic viscosity coefficient,
is the gradient operator,ρ is the fluid density,p′
is the instantaneous pressure,ν is the kinematic viscosity coefficient,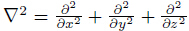 is
the Laplacian operator,and F is the body force. Using the Oseen transformation[14, 15],the
instantaneous velocity V ′ and the instantaneous pressure p′ can be represented as
is
the Laplacian operator,and F is the body force. Using the Oseen transformation[14, 15],the
instantaneous velocity V ′ and the instantaneous pressure p′ can be represented as
 |
| Fig. 2. Illustration of velocity gradient near wall surface |
Using Eq. (3) and neglecting the terms related to the second and higher orders of small parameters,Eqs. (1) and (2) can be rewritten as follows:
Looking at non-dimensional parameters,we can consider the Reynolds number as Re = ,where Fr is the Froude number,the dimensionless velocity is
,where Fr is the Froude number,the dimensionless velocity is  ,and the dimensionless pressure is
,and the dimensionless pressure is  . The dimensionless coordinates are
. The dimensionless coordinates are  . The dimensionless time is
. The dimensionless time is  . The dimensionless averaged velocity
is
. The dimensionless averaged velocity
is  . The corresponding equations of each εth-order are
. The corresponding equations of each εth-order are
Substituting the dimensionless parameters into Eq. (5),we have the hydrostatic pressure equation as
Substituting the dimensionless parameters into Eq. (6) and removing the brackets for simplicity,we have
Taking divergence of both sides of the second equation of Eq. (8) and using the continuity equation (the first equation of Eq. (8)),we have
Therefore,the ε1th-order pressure function can satisfy the Poisson equation and is directly proportional to the vertical velocity rate along the flow direction. Taking the curl of both sides of the second equation of Eq. (8) and the continuity equation (the first equation of Eq. (8)),we have
Assuming a vertical two-dimensional problem,we have ν = 0 and  = 0. Equation (10)
can be simplified as
= 0. Equation (10)
can be simplified as
We consider an analytic function in the form of
Then,we have
The above equation is the ε1th-order vorticity function differential equation. 3 Solution to vorticity function equation
We assume that Eq. (13) has a variable separable solution in the form of
Substituting Eq. (14) into Eq. (13) and considering the quasi-periodicity of T (t),we have
where ω is an undetermined constant,and i is the imaginary unit. Equation (15) can be presented asIn Eq. (16),the solution to the first equation is
where A is a constant. The second equation has quasi-periodicity variations along the xdirection. The solution is assumed to be in the form of where n =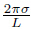 is the wave number,σ = 1,2,3,· · · ,and L is the wavelength. We can obtain a
set of solutions corresponding to each value of n. Without loss of generality,we can solve the
equation for any value of n. Substituting Eq. (18) into the second equation of Eq. (16) yields
is the wave number,σ = 1,2,3,· · · ,and L is the wavelength. We can obtain a
set of solutions corresponding to each value of n. Without loss of generality,we can solve the
equation for any value of n. Substituting Eq. (18) into the second equation of Eq. (16) yields
Let Kn =  and ξn = −(n2 + iωRe)Kn-2 − iKnz
. Then,Eq. (19) can be rewritten as
and ξn = −(n2 + iωRe)Kn-2 − iKnz
. Then,Eq. (19) can be rewritten as
Equation (20) is the complex variable form of the Airy equation[16]. Using ξn = −ξ′n transform,we can obtain the equivalent equation as
4 Contour integral and solution to complex variable Airy equation 4.1 Contour integralWe consider a complex analytic function as
For the contour Γ integral,w and ξn are complex variables. The contour Γ starts from the origin O and goes to A along the real axis R. The length of OA is ρ (ρ > 0). The arc continues to B,which has the position of ρeiπ/6. Then,it returns to the origin O along the straight-line BO. Then,it starts from the origin O and goes towards C along a straight line,which has the position of ρei5π/6. After that,the arc goes to D,which is on the imaginary axis at the position iR,as shown in Fig. 3. According to the Cauchy integral theorem along the closed curve[17], f(w) can be resolved in the contour. Therefore,the integral is zero along the contour Γ,i.e.,
 |
| Fig. 3. Illustration of contour integral |
The following part studies the solution for each integral section. In order to compute the OA integral section,which is along the real axis,we consider w = τ,where τ is a real number. We have
In order to compute the  integral section,which is along an arc of radius ρ,we consider
w = ρeiθ and dw = iρeiθdθ. We have
integral section,which is along an arc of radius ρ,we consider
w = ρeiθ and dw = iρeiθdθ. We have
The integral is independent of ρ. Then,we substitute ei3θ = cos(3θ) + i sin(3θ) into the above equation (25),and we have

When ρ → ∞,the convergence of Eq. (25) is related to  . When θ varies between 0
and
. When θ varies between 0
and  ,3θ varies between 0 and
,3θ varies between 0 and  . Therefore,cos(3θ) > 0. We have
. Therefore,cos(3θ) > 0. We have

Figure 4 shows that the amplitude of  changes with ρ. When
changes with ρ. When  ,
and
,
and  tends to 0 faster than
tends to 0 faster than  . We compute the BC section integral,which is
along the straight line of τeiπ/6,by letting w = τeiπ/6 = τeiπ(2/3−1/2) = −iτe2π/3. We have
. We compute the BC section integral,which is
along the straight line of τeiπ/6,by letting w = τeiπ/6 = τeiπ(2/3−1/2) = −iτe2π/3. We have
 |
| Fig. 4. Variation of contour integral |
We compute the OC section integral,which is along the straight line of τei5π/6,by letting w = τei5π/6 = −τeiπ/6 = −iτe−i2π/3. We have
We compute the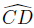 integral,which is along an arc of radius ρ,by letting w = ρeiθ and
dw = iρeiθdθ. We have
When θ varies between
integral,which is along an arc of radius ρ,by letting w = ρeiθ and
dw = iρeiθdθ. We have
When θ varies between 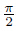 and
and 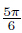 ,3θ varies between
,3θ varies between 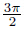 and
and 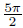 ,and cos(3θ) ≥ 0. Therefore,
we have
,and cos(3θ) ≥ 0. Therefore,
we have

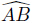 and
and 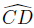 integrals tend to zero. Then,by
looking at Eq. (23),we have an integral summation along the path ρeiπ/6 ~ 0 and the path
0 ~ ρei5π/6.
4.2 Solution to complex variable Airy equation
integrals tend to zero. Then,by
looking at Eq. (23),we have an integral summation along the path ρeiπ/6 ~ 0 and the path
0 ~ ρei5π/6.
4.2 Solution to complex variable Airy equationWe assume the solution to the complex variable Airy equation in the form of
where Hnj is an undetermined constant,and j = 1,2. We substitute Eqs. (31) and (32) into the complex variable Airy equation. Noticing that 2π/3 = π/2 + π/6,we have

The above equation (33) is the solution to the equivalent Airy equation (21). The results show that the left side of Eq. (30) satisfies the complex variable Airy equation. Therefore, we can prove that the right side of Eq. (30) is also the solution to the complex variable Airy equation. We can write the general solution form as
We assume a solution in the form of The general solution to the complex variable Airy equation can be written asSubstituting the solution into Eq. (14),we can obtain the solution of nth-order vortex function as
where Hn1,Hn2,n,and ω can be determined by the boundary conditions and the physical conditions. 5 Velocity solution of pulsatile flow field 5.1 Velocity equation
According to the vorticity equation and the continuity equation,we have
Then,we can have Considering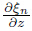 = −iKn and Eq. (37),we have
where
5.2 Homogeneous solution and special solution of horizontal velocity component
= −iKn and Eq. (37),we have
where
5.2 Homogeneous solution and special solution of horizontal velocity component We assume u = U(z) exp(i(nx + ωt)) and substitute it into Eq. (40). We have
The homogeneous solution to Eq. (45) is in the form of
where Dn1 and Dn2 are constant,which are determined by the boundary conditions. We assume the special solution to Eq. (45) in the form of where Gx(τ),Kx(τ),Qx(τ),and Sx(τ) are complex functions. Substituting U2 into Eq. (45) yields If we compare the coefficients,we have We can obtain the special solution of horizontal velocity as where the τ integral is from 0 to ∞,and there exists a singularity. Therefore,we need to solve this problem by means of singularity contour integral. 5.3 Singularity contour integral of horizontal velocityWe assume a complex function in the form of
In the τ plane,the contour starts from the origin O,goes to A,and then goes to C passing
B. ABC is a semicircle arc of radius ε. Here,we bypass the singularity 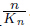 . Then,we go from
C to D along the τ-axis. From D,an arc of radius ρ in the counter-clockwise direction reaches
the point E. Then,from E,we go back to O along
. Then,we go from
C to D along the τ-axis. From D,an arc of radius ρ in the counter-clockwise direction reaches
the point E. Then,from E,we go back to O along  . Then,we go from the origin O to
F along
. Then,we go from the origin O to
F along  with an arc of radius ρ in the clockwise direction of the point G on the iτ-axis.
Finally,we go from G to the origin O along the iτ-axis,as shown in Fig. 5. Along the contour
with an arc of radius ρ in the clockwise direction of the point G on the iτ-axis.
Finally,we go from G to the origin O along the iτ-axis,as shown in Fig. 5. Along the contour  ,the integral is zero,and we have
,the integral is zero,and we have
 |
| Fig. 5. Illustration of trajectory of singularity contour integral |
In the straight part O → E,we have w = τ and dw = dτ.
In the curved arc ,we have w =
,we have w = 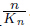 + εeiθ and dw = iεeiθdθ. We have
When ε → 0,we use L’Hospital’s rule and we have
+ εeiθ and dw = iεeiθdθ. We have
When ε → 0,we use L’Hospital’s rule and we have

In the curved arc  ,we have w = ρeiθ and dw = iρeiθdθ.
,we have w = ρeiθ and dw = iρeiθdθ.
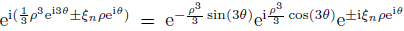 . When ρ → ∞,the convergence of
Eq. (55) depends on
. When ρ → ∞,the convergence of
Eq. (55) depends on 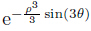 . When θ varies between 0 and
. When θ varies between 0 and 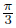 ,3θ varies between 0 and π,
and sin (3θ) ≥ 0. Therefore,we have
,3θ varies between 0 and π,
and sin (3θ) ≥ 0. Therefore,we have



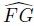 ,we have w = ρeiθ,dw = iρeiθdθ,and
where
,we have w = ρeiθ,dw = iρeiθdθ,and
where 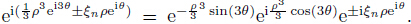 . When ρ → ∞,the convergence of
Eq. (57) depends on
. When ρ → ∞,the convergence of
Eq. (57) depends on 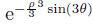 . When θ varies between
. When θ varies between 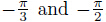 ,3θ varies between −π
and
,3θ varies between −π
and 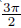 ,and sin(3θ) ≥ 0. Therefore,we have
,and sin(3θ) ≥ 0. Therefore,we have

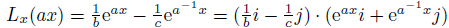 ,where i and j are
perpendicular unit vectors. Lx(ax) can be extended to any dimensional vector. In this study,
a = ei2π/3,b = (Knτ)2e−i2π/3− n2,c = (Knτ)2ei2π/3− n2,and x = −i(±ξnτ). The properties
of Lx(ax) derivatives are as follows:
,where i and j are
perpendicular unit vectors. Lx(ax) can be extended to any dimensional vector. In this study,
a = ei2π/3,b = (Knτ)2e−i2π/3− n2,c = (Knτ)2ei2π/3− n2,and x = −i(±ξnτ). The properties
of Lx(ax) derivatives are as follows:

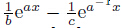 = Lx(ax). We substitute Eq. (60) into Eq. (50),
and the velocity special solution in the horizontal direction is obtained as
= Lx(ax). We substitute Eq. (60) into Eq. (50),
and the velocity special solution in the horizontal direction is obtained as
The velocity general solution in the horizontal direction is
where N = −(n2 + iωR)Kn2 and M = n/Kn. 5.4 General solution and special solution of vertical velocity componentWe assume w = W(z) exp(i(nx + ωt)) and substitute w into Eq. (40). We have
The homogeneous solution to Eq. (63) can be presented as where En1 and En2 are undetermined coefficients. The special solution to Eq. (63) can be presented as where Gz(τ),Kz(τ),Qz(τ),and Sz(τ) are the complex functions. Then,substituting the special solution W2 into Eq. (63),we have Comparing the coefficients,we have We can obtain the special solution of velocity in the vertical direction as The above equation (68) contains singularity. Therefore,we need to solve this problem by means of singularity contour integral. 5.5 Singularity contour integral of vertical velocityWe assume an analytic complex function as
The contour integral is computed term by term using the same method discussed in Section 5.3. Therefore,Eq. (68) can be presented asThe vertical velocity is presented as 6 Pressure function in shear flow field
In the Couette flow problem,the pressure gradient is used to find the velocity distribution. However,in the study,the velocity distribution is used to find the pressure. Rewrite Eq. (71) as
We consider the pressure in the form of p = P (z) exp(i(nx+ωt)) and substitute p into Eq. (9). We have

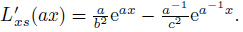 7 Boundary conditions for finite problems
7 Boundary conditions for finite problemsIn order to determine the undetermined constants in Eqs. (37),(62),(71),and (81),the boundary conditions of the vorticity solution,the velocity solution,and the pressure solution are discussed in the following sections. The boundary conditions have various forms,but determining the boundary conditions of the complex problems has never been an easy task. A simple form of the boundary condition is presented in the following sections,and the variations of the solutions are discussed. 7.1 Vorticity solution
In the vorticity solution,the complex variable Airy functions Aj(ξn) and Bj(ξn) satisfy the
complex variable Airy equation. When ξn is determined,the complex variable Airy function
cannot converge at the same time,if ξn = −a − ib,a > 0,and b > 0,where both a and b
have finite values. The integral
∫0∞ exp dτ converges. However,the convergence
of the integral i
dτ converges. However,the convergence
of the integral i  is determined before ξn. We consider positive sign
as divergence and negative sign as convergence,respectively. Therefore,Aj(ξn) diverges,and
Bj(ξn) converges. Removing the part related to Aj(ξn) and letting Hn1 = 0,we can obtain the
vorticity solution as
is determined before ξn. We consider positive sign
as divergence and negative sign as convergence,respectively. Therefore,Aj(ξn) diverges,and
Bj(ξn) converges. Removing the part related to Aj(ξn) and letting Hn1 = 0,we can obtain the
vorticity solution as
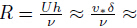 11.6[18],where v* is the friction velocity,δ is the boundary
layer thickness,and ν is the kinematical viscosity coefficient. The circular frequency is considered to be equal to ω = 18.84 s−1,which is obtained by the turbulent energy. The vortex wavelength is L = 2πh. The wave number is n = σ/h,where the relative depth is h = 1.0 m and σ =
1,2,3,· · · ,100. Therefore,we can obtain the variation of the complex variable parameter ξn as
shown in Fig. 6. When the value of n increases,the real part of ξn increases,the imaginary part of ξn approaches a stable value,and the water depth of imapinary part decreases. Figures 7
and 8 show the variation of Bj(ξn) along the vertical direction. We can see that the value of
Bj(ξn) is larger at the region close to the wall surface. This implies that when the value of n
increases,the value of Bj(ξn) becomes larger.
11.6[18],where v* is the friction velocity,δ is the boundary
layer thickness,and ν is the kinematical viscosity coefficient. The circular frequency is considered to be equal to ω = 18.84 s−1,which is obtained by the turbulent energy. The vortex wavelength is L = 2πh. The wave number is n = σ/h,where the relative depth is h = 1.0 m and σ =
1,2,3,· · · ,100. Therefore,we can obtain the variation of the complex variable parameter ξn as
shown in Fig. 6. When the value of n increases,the real part of ξn increases,the imaginary part of ξn approaches a stable value,and the water depth of imapinary part decreases. Figures 7
and 8 show the variation of Bj(ξn) along the vertical direction. We can see that the value of
Bj(ξn) is larger at the region close to the wall surface. This implies that when the value of n
increases,the value of Bj(ξn) becomes larger.
 |
| Fig. 6. Variation of complex variable parameter ξn |
 |
| Fig. 7. Real part of Bj(ξn) along vertical profile |
 |
| Fig. 8. Imaginary part of Bj(ξn) along vertical profile |
In order to find the velocity solution,we look at Eqs. (62) and (71) and have
The bottom velocity boundary conditions are u|z=0 = 0 and w|z=0 = 0. The upper velocity boundary conditions are u|z=h = 0 and w|z=h = 0. Then,we have andWe substitute the vorticity solution parameters into Eqs. (90) and (91),and we obtain the velocity distribution along the vertical direction (as shown in Figs. 9 and 10).
 |
| Fig. 9. Horizontal relative velocity profiles along vertical direction |
 |
| Fig. 10. Vertical relative velocity profiles along vertical direction |
It can be observed from Figs. 9 and 10 that the horizontal velocity distribution along the vertical direction is consistent with the vertical velocity distribution. When n is small,the fluctuation of the velocity amplitude is vertically symmetric. We can observe a downward shift of the curve centroid with the increase in the value of n. In this case,the upper curvature decreases and the bottom curvature increases when n > 7. When n > 10,the bottom of the curves appears to be folded. That is the reason for the vortex formation close to the wall. 7.3 Pressure solution
Substituting the constant values determined by the vorticity solution into Eq. (81) yields
The upper boundary condition for the relative pressure is p|z=h = 0. We assume that the bottom relative pressure is zero without the vorticity disturbance,which gives p|(z=0,Hn2=0) = 0. Then,we have
and If we know the time and the x-direction spatial position and substitute the vorticity solution parameters into Eq. (95),we can obtain the pressure function distribution along the vertical direction (as shown in Fig. 11). When n is small,the pressure presents a linear distribution. When n = 9,the upper part of curve is mostly convex. When n > 9,the curve swings toward the negative direction. When n = 11,the negative pressure amplitude appears near the bottom. |
| Fig. 11. Relative pressure profiles along vertical direction |
The vorticity spatial distribution can be obtained using Eq. (83) as shown in Fig. 12. It can be observed from Fig. 12 that a larger value of vorticity appears at a region close to the bottom of the wall. The vorticity has an alternatively positive-negative pattern,when the relative water depth is h ≥ 0.3 and the relative vorticity is |φ′| < 0.1.
 |
| Fig. 12. Vorticity profile in vertical plane |
The particle relative trajectory formula can be obtained from Eqs. (90) and (91),i.e.,
We consider the initial position as (x0,z0)=(0.0,0.2). Here,we study two cases,i.e.,n=1 m−1 and n=10 m−1. Figures 13 and 14 show the particle relative trajectories for low wave numbers and high wave numbers,respectively. Figures 13(a)-13(d) show the mean flow equal to U0.2 = 0.0,U0.2 = 0.5umax,U0.2 = 1.0umax,and U0.2 = 3.0umax,respectively,where U0.2 denotes the mean velocity at the relative water depth equal to 0.2,and umax denotes the maximum horizontal velocity of particle. It can be observed from Fig. 13 that when the mean velocity exists,the particle trajectory is more symmetric. When no mean velocity exists,the particle trajectory takes the shape of an ellipse. The waveform shows symmetrical distribution along the x-direction and has stable shape. |
| Fig. 13. Particle relative displacement trajectories in case of low wave number |
 |
| Fig. 14. Particle relative displacement trajectories in case of high wave number |
It can be observed from Fig. 14 that,when the wave number is large,the particle trajectory has both asymmetric shape and inclination. When no mean velocity exists,the particle trajectory is inclined in the form of an ellipse. When the mean velocity increases,the waveform unfolds successively. It can be observed that larger wave number leads to earlier stability loss. 8.3 Distribution of pressure function
Figure 15 shows the pressure function (see Eq. (95)) distribution in a vertical plane. It can be observed that a larger value of the relative pressure appears at the region close to the bottom of the wall. The relative pressure has an alternatively positive-negative pattern closer to the bottom of the wall. Changes of the positive-negative amplitude are more violent when the relative water depth is h ≥ 0.4 and the relative pressure is |p′| < 0.1.
 |
| Fig. 15. Pressure function profiles in vertical plane |
The velocity fluctuations can be presented as different frequency components using statistical average methods. In this paper,the velocity fluctuation is presented using Eqs. (90) and (91) and a simple combination solution,
where Ai and Bi (i = 1,2,3,4) are undetermined parameters,and n1 and n2 are two sets of different wave numbers. Then,we have

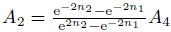 . If we consider a=-A4,we have
Similarly,
The distribution curves of
. If we consider a=-A4,we have
Similarly,
The distribution curves of 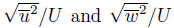 can be obtained by selecting the appropriate
values of parameters a,n1,n2 and a′,n′
1,n′2. Figures 16 and 17 show the comparison between
the theoretical results of the velocity fluctuation and the measured data. The measured data
are obtained from Prashun,Raichlen,Rao,and McQuivey’s experiments results[19],which is
Case 1. Figures 18 and 19 show the comparison between the theoretical results of the velocity
fluctuation and the measured data. The measured data are obtained from Grass’ s experiments
results[19],which is Case 2. Table 1 shows the selected parameters.
can be obtained by selecting the appropriate
values of parameters a,n1,n2 and a′,n′
1,n′2. Figures 16 and 17 show the comparison between
the theoretical results of the velocity fluctuation and the measured data. The measured data
are obtained from Prashun,Raichlen,Rao,and McQuivey’s experiments results[19],which is
Case 1. Figures 18 and 19 show the comparison between the theoretical results of the velocity
fluctuation and the measured data. The measured data are obtained from Grass’ s experiments
results[19],which is Case 2. Table 1 shows the selected parameters.
 |
| Fig. 16. Horizontal fluctuation profiles along vertical direction (Case 1) |
 |
| Fig. 17. Vertical fluctuation profiles along ver- tical direction (Case 1) |
 |
| Fig. 18. Horizontal fluctuation profiles along vertical direction (Case 2) |
 |
| Fig. 19. Vertical fluctuation profiles along ver- tical direction (Case 2) |
We consider the turbulent shear force formula as
The following equation is obtained by the same process as Eqs. (102) and (103):Figures 20 and 21 are prepared using the parameters provided in Table 2. It can be observed from Fig. 16 to Fig. 21 that the variation of experimental data agrees well with that of the theoretical results.
 |
| Fig. 20. Comparison of theoretical results and experimental data of dimensionless shear stress (Case 1) |
 |
| Fig. 21. Comparison of theoretical results and experimental data of dimensionless shear stress (Case 2) |
(i) This paper uses the Navier-Stokes equations and applies the Oseen transformation in order to find the velocity fluctuation in a finite problem using the vorticity function,the velocity function,and the pressure function in a shear flow field.
(ii) The complex solution of the Airy function is studied using a new contour integral method. Then,the vorticity function,the velocity function,and the pressure function are analytically solved in a vertical linear gradient flow distribution.
(iii) This paper presents an Lx-function form of the third derivative circulation to simplity the solution.
(iv) The vorticity and pressure in a linear gradient flow distribution are computed for given boundary conditions. The stability of particle motion trajectories is analyzed.
(v) A comparison between the theoretical results and the experimental measurements is provided with satisfactory agreement.
Acknowledgements The authors thank the State Key Laboratory of Hydraulic Engineering Simulation and Safety (Tianjin University) for support and thank Prof. R. A. DALRYMPLE of Johns Hopkins University for assistance.| [1] | Prandtl, L., Oswatitsch, K., and Wieghardt, K. Introduction to Fluid Mechanics, Science Press, 295-298 (1969) |
| [2] | Drazin, P. G. and Reid, W. H. Hydrodynamic Stability, 1st ed., Cambridge University Press, 1-24 (1981) |
| [3] | Schlichting, H. Boundary-Layer Theory, 7th ed., McGraw-Hill Company (1979) |
| [4] | McQuivey, R. S. and Richardson, E. V. Some turbulence measurements in open channel flow. J. Hyd. Div., Proc., Amer. Soc. Civil Engrs., 95(HY1), 209-223 (1969) |
| [5] | Esfahanian, V., Hejranfar, K., and Sabetghadam, F. Linear and nonlinear PSE for stability analysis of the Blasius boundary layer using compact scheme. Journal of Fluids Engineering, 123(3), 545-550 (2001) |
| [6] | Li, D. M., Zhang, H. P., and Gao, Y. X. Series perturbations approximate solutions to N-S equations and modification to asymptotic expansion matched method. Applied Mathematics and Mechanics (English Edition), 23(8), 963-972 (2002) DOI 10.1007/BF02437802 |
| [7] | Sumner, D. and Akosile, O. O. On uniform planar shear flow around a circular cylinder at sub-critical Reynolds number. Journal of Fluids and Structures, 18, 441-454 (2003) |
| [8] | Wang, Z., Yeo, K. S., and Khoo, B. C. Spatial direct numerical simulation of transitional boundary layer over compliant surfaces. Computers and Fluid, 34, 1062-1095 (2005) |
| [9] | Huang, Z. F. and Zhou, H. Inflow conditions for spatial direct numerical simulation of turbulent boundary layers. Science in China Series G: Physics, Mechanics and Astronomy, 51(8), 1106-1115 (2008) |
| [10] | Ehrenstein, U., Nagata, M., and Rincon, F. Two-dimensional nonlinear plane Poiseuille-Couette flow homotopy revisited. Physics of Fluids, 20(6), 064103 (2008) |
| [11] | Gires, P. Y., Danker, G., and Misbah, C. Hydrodynamic interaction between two vesicles in a linear shear flow: asymptotic study. Physical Review, 86(1), 011408 (2012) |
| [12] | Kádár, R. and Balan, C. Transient dynamics of the wavy regime in Taylor-Couette geometry. European Journal of Mechanics-B/Fluids, 31, 158-167 (2012) |
| [13] | Ashrafi, N. and Hazbavi, A. Flow pattern and stability of pseudoplastic axial Taylor-Couette flow. International Journal of Non-Linear Mechanics, 47(8), 905-917 (2012) |
| [14] | Yi, J. Fluid Dynamics, Higer Education Press, Beijing, 274-280 (1982) |
| [15] | Qian, W. Singular Perturbation Theory and Its Application in Mechanics, Science Press, Beijing, 209-216 (1981) |
| [16] | Liu, S. and Liu, S. Special Functions, China Meteorological Press, Beijing, 403-508 (1988) |
| [17] | Wang, Z. and Guo, D. Special Functions, Science Press, Beijing, 381-506 (1979) |
| [18] | Yalin, M. S. Mechanics of Sediment Transport, 2nd ed., Pergamon Press, California, 1-60 (1977) |
| [19] | Qian, N. and Wan, Z. H. Mechanics of Sediment Transport, Science Press, Beijing, 82-110 (1986) |
 2015, Vol. 36
2015, Vol. 36






























































































