1 Introduction The gravity-induced film flow along a solid surface has extensive importance in the configurations of heat and mass transfer equipments such as coolers,evaporators,and trickling filters. A series of investigations have been carried out towards the understandings of the mechanisms of liquid flow in a thin film since Fulford^[1] suggested a great variety of analytical approaches for the thin film flow phenomena. Among those studies,Andersson et al.^[2] considered the natural and forced thermal convection in a gravity-driven liquid film flow along a vertical solid surface with the Bonssinesq approximation being applied to account for buoyancy. Andersson and Ytrehus^[3] investigated a gravity-induced film flow along a wedge and obtained an exact reference solution based on the assumption that the boundary layer is not interacted with the free surface of the film. Pop et al.^[4] argued that Andersson’s similarity solution^[3] cannot be possible if there is fluid injection or suction through the porous wall. To overcome this difficulty, they suggested a non-similarity approach to solve this frequently encountered mass transfer problem. Ammarah and Xu^[5] extended Andersson’s problem^[2] to the case that the convective heat transfer is allowed through the vertical wall. They then presented a uniformly analytical solution with explicit form. Andersson and Irgens^[6] presented a theoretical analysis based on the similarity approach for a non-Newtonian power-law fluid flow in a thin film flowing down along a vertical plate. Shang and Andersson^[7] made an analysis for the film flow and heat transfer of a non-Newtonian power-law fluid down along an inclined flat sheet and provided a non-similarity solution for the heat transfer problem. It is worth noticing that there have been a lot of debates on the validity of the no-slip boundary condition and a number of experimental results,which reveal that this assumption could lead to several different results. The no-slip condition at the solid-fluid interface,which indeed has the practical importance,states that there is no relative movement between the fluid and the solid surface on the interface. The complex behavior at a liquid-solid interface involves the interplay of many physicochemical parameters, including wetting,shear rate,surface charge,surface roughness,pressure,impurities, and dissolved gas. Nevertheless,it is known through the experiments that a sufficiently large amount of roughness of solid surface can generate no slip^[8,9]. Recently,Yuan and Zhao^[10] considered a precursor film in the wetting and electrowetting process,in which they introduced the molecular dynamics simulations to explore the atomic details and the transport properties of the precursor film in dynamic wetting and concluded that the precursor film is solid-like and no-slip on the boundary. Then,they analyzed the dynamic wetting of a droplet on a lyophilic pillars by considering both the multiscale combination method of experiments and molecular dynamics simulations^[11]. Their work gave an insight of the liquid-solid interactions of thin film with its rough surface from the continuum to atomic level.

Recently,nanofluids have received considerable attentions in the field of thermal sciences owing to their great potentials on the improvement of heat transfer properties,such as thermal conductivity,thermal diffusivity,viscosity,and convective heat transfer coefficient relative to the traditional heat transfer fluids. Also nanofluids have the potential applications in the field of enhanced oil recovery (EOR)^[12,13],because they are proven to be good EOR agents and effective detergents for cleaning oil from a surface. Several mathematical models such as the homogenous model^[14],the dispersion model^[15],and the Buongiorno model^[16] have been proposed to predict the behaviours of nanofluids. Particularly,the Buongiorno model^[16],which is formulated based on the mechanics of the nanoparticle/base-fluid relative velocity,gains most acceptance. By means of this model,Kuznetsov and Nield^[17] examined the natural convection nanofluid flow past a vertical plate,in which they used the simplest boundary conditions with both the temperature and the nanoparticle fraction distributions along the wall being uniform. Nield and Kuznetsov^[18] made an extension of the classic Cheng-Minkowycz^[19] problem by assuming that the vertical plate is embedded in a porous medium saturated by a nanofluid. In the same vein,some studies have been done for a number of heat transfer problems among which typical work can be found in Refs. ^[20,21,22]. Very recently,Nield and Kuznetsov^[23] noticed that the active control of the nanoparticle volume fraction at the boundary used by Buongiorno^[16] could be physically unrealistic for a number of natural and forced convection problems. They then improved the model by introducing the passively controlled boundary condition to replace the actively controlled boundary condition.

Bioconvection has many applications in modeling oil and gas-bearing sedimentary basins and microbial EOR so that some researchers devote themselves for the investigation of the mechanism of various bioconvection problems in suspensions of solid particles. The microbial EOR is a new technology going on in oil and gas industries to increase oil recovery. This technique includes the injection of selected microorganisms into the reservoir and by their in situ multiplication they reduce the residual oil left in the reservoir after secondary recovery is exhausted. Kuznetsov and Avramenko^[24] initiated the investigation of bioconvection in a suspension of gyrotactic microorganisms in a layer with finite depth. Their idea was then followed and extended by Geng and Kuznetsov^[25,26,27],Kuznetsov^[28,29,30],and Kuznetsov and Geng^[31] for various bioconvection problems. It should be noted that Kuznetsov^[32] analyzed a bioconvection within the horizontal fluid layer in a suspension that contains both solid particles in nanoscale and gyrotactic microorganisms in the fluid,which is heated from the bottom. In the same context,Tham et al.^[33,34] considered the mixed convection flows over a sphere and past a cylinder in a stream flowing vertically upwards for the heated or cooled body. In both cases,the saturated porus medium contains both nanoparticles and gyrotactic microorganisms. It is worth mentioning to this end that Xu and Pop^[35] noticed that the nanofluid model used in Refs. ^[32,33,34] were the actively controlled model,which could be physically unrealistic as concluded by Nield and Kuznetsov^[23]. They therefore suggested to introduce the passively controlled nanofluid model to investigate the bioconvection phenomena.

Bioconvection in nanofluids has great potential in enhancing mass and heat transport and mixing,especially in micro-volumes,and also to improve the stability of nanofluids. A combination of nanofluids and bioconvection thus is attractive for the design of novel microfluidic devices. Therefore,a better understanding of such a physical phenomenon at the fundamental level is very necessary. The main purpose of this paper is to investigate the mixed bioconvection flow of a gravity-driven nano-liquid film that contains both nanoparticles and gyrotactic microorganisms down along a convectively heated wall. Different from the previous work of Kuznetsov^[32] and Tham et al.^[33,34],we study both the actively and the passively controlled models for simplification of this bioconvection problem. In particular,this work exhibits an analytical approach for nanofluid bioconvection based on physical mechanisms responsible for the slip velocity between the nanoparticles and the base fluid,such as Brownian motion and thermophoresis. The problem under consideration embodies five field equations including the conservation of total mass,momentum,thermal energy,and nanoparticles and microorganisms, which are reduced to a set of five ordinary differential equations with two kind of boundary conditions (the actively and the passively controlled boundary conditions for the nanoparticle volume fraction). The resulting equations are then solved numerically by means of a finite difference technique. Besides,the effects of various physical parameters on the distributions of velocity,temperature,nanoparticle volume fraction,and density of motile microorganisms are graphically presented. Furthermore,approximate expressions with high precision for variations of the local skin friction,the local Nusselt number,the local wall mass flux ,as well as the local wall motile microorganisms flux with some physical parameters are obtained and discussed, respectively. 2 Mathematical descriptions

Consider a two-dimensional thin liquid film of the fluid containing both nanoparticles and microorganism,which falls downwards along a vertical solid surface due to gravity. As shown in Fig. 1,the uniform incoming flow on the right side of the plate has a constant temperature T_∞ at x = 0,while the fluid on the left side of the plate has another constant temperature T_f . The thin film is cooled or heated due to the convection through the plate. It is assumed that the nanofluid is dilute so that the bioconvection instability can be avoided. It is also assumed that the nanoparticles suspended in the base fluid are stable and do not agglomerate in the fluid. Both the active and the passive control of nanoparticle volume faction at the boundary (on the solid wall) are considered. The microorganisms are assumed to have constant distributions on the wall. It is worth mentioning that the base fluid is water so that the microorganisms can survive. It is also assumed that the existence of nanoparticles has few effect on the motion of the microorganisms.

Keeping all these assumptions in view and using the model proposed by Kuznetsov and Nield^[18],the conservations of total mass,momentum,thermal energy,nanoparticles,and microorganisms are described by the following partial differential equations:

where v is the velocity vector of the flow with u and v being the velocity components in the x-and y-directions,respectively,T is the temperature,C is the nanoparticle volumetric fraction,N is the number density of motile microorganisms,j is the vector of the flux of microorganisms,p is the pressure,g is the acceleration due to gravity,ρf,μ,β,and α are,respectively,the density, the viscosity,the volumetric volume expansion coefficient,and the thermal diffusivity of the fluid,τ = (ρc)_p/(ρc)_f is a parameter with (ρc)_p being the heat capacity of the nanoparticle and (ρc)_f being the heat capacity of the nanofluid,DB is the Brownian diffusion coefficient,D_T is the thermophoretic diffusion coefficient,Δρ = ρ_cell − ρ_f∞ is the density difference between a cell and base fluid density at far field,and γ is the average volume of a microorganism. Here, the subscriptions p,f,w,and f∞ denote,respectively,the solid particles,the nanofluid,the wall,and the base fluid at far field.

Following Ref. ^[32],we expand the flux of microorganisms j as

where D_m is the diffusivity of microorganisms,and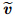 is the average swimming velocity vector of the oxytactic microorganism defined by in which b is the chemotaxis constant,and W_c is the maximum cell swimming speed.

Applying the Oberbeck-Boussinesq approximation to the buoyancy terms and choosing a suitable reference pressure

the momentum equation can be linearized. Consequently,using the boundary layer approximations, the whole system is transformed to The above equations are solved subjecting to the following two sets of boundary conditions (two models):

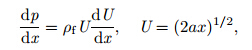
(i) The actively controlled nanofluid model

(ii) The passively controlled nanofluid model

In the above two equations,h_f (x) is the heat transfer coefficient due to T_f,ν = μ/ρf is the kinematic viscosity,and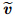 = 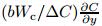. Note that,in order to satisfy the boundary conditions at infinity,we have to set N_∞ = 0.

Two sets of similarity variables are defined corresponding to the following two models:

(i) In the actively controlled nanofluid model,

(ii) In the passively controlled nanofluid model,

where ψ(x,y) is the stream function given that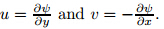

Substitute the above two kinds of similarity variables into (8)-(12). The continuity equation (8) is satisfied automatically,and the rest of equations take the forms of

Two kinds of boundary conditions (two models) are expressed as follows.

(i) The actively controlled model

(ii) The passively controlled model

In (17)-(22),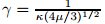 is the reduced heat transfer parameter,G_r,N_r,R_b,N_b,N_t,P_r,L_e,S_c,and P_e are the Grashof number,the bouncy-ratio parameter,the bioconvection Rayleigh number,the Brownian motion parameter,the thermophoresis parameter,the Prandtl number, the Levis number,the Schmidt number,and the bioconvection Peclet number,respectively, which are defined as In (23),we have a = g,which indicates that the flow is induced by gravity. Note that for the two investigated models,the definitions of the Brownian motion parameter are different, namely,N_b^a denotes the Brownian motion parameter in the actively controlled model and N_p^b denotes that in the passively controlled model. In the following part,we will use N_b to express them to avoid confusion.

The physical quantities of practical interests are the local skin friction,the local Nusselt number,the local wall mass flux,and the local wall motile microorganisms flux,which are defined as

where

Substituting (15) and (16) into (24),we obtain

where Re = Ux/ν is the local Reynolds number. Here,we use the term Re⁻¹/²Q_mx to represent Re⁻¹/²Q_mx^a and Re⁻¹/²Q_mx^p. 3 Results and discussion

The fully coupled nonlinear ordinary differential equations (17)-(20) with the boundary conditions (21) and (22) are solved by means of a highly efficient finite difference technique of quasi-linearization^[36]. This approach gives an iterative scheme which requires step-by-step integrations of linear differential equations until the convergence is achieved. The initial values are given based on the boundary conditions (21) and (22) as

The boundary conditions are forced to be satisfied at each iterative step. To apply the boundary condition at far field,the calculation range for η is taken as η_∞ = 10,which is divided evenly into 200 discrete segments. The error is defined,based on the rule that the absolute difference on each node for all the calculating functions between two successive steps of the iteration is less than some control error,as

in which Er_C is the control error,l > 1 is the iteration step,and G represents any function of f,θ,φ,and w. Here,we set Er_C ≤ 1 × 10−6 for all considered cases,which is found to be adequate in the present computations. Further to check the accuracy and validity of the proposed technique,a comparison between the current results and those given by an HAM package named BVPh 2.0^[37] is made,and very excellent agreement is found,as graphically illustrated in Fig. 2.

We then examine the effects of the heat transfer parameter γ on the profiles of the velocity, the temperature,the concentration of nanoparticles,as well as the density of motile microorganisms. As shown in Fig. 3,γ has an evident effect on f'(η) that the larger the value of γ is,the greater the velocity is. But this effect becomes negligibly small as γ is considerably large. Physically γ represents the heat transfer capability of the vertical surface that means its increase introduces more heat energy into the thin film due to the convection through the wall,which leads to the increase of the buoyancy,as such the velocity enlarges accordingly. When γ is considerably large,the plate almost has the same temperature as the fluid on the left side of the plate. In such a situation,the flow velocity approaches to the maximum value. In Fig. 3(a),we also notice that f'(η) given by the passively controlled model is always larger than that by the actively controlled model. Particularly,the effect of the buoyancy leads to a velocity overshoot for the passively controlled model,i.e.,f'(η) > 1,which does not happen in the actively control model.

The variations of θ(η) along η with different values of γ are plotted in Fig. 3(b). It is seen that the increase of γ leads to the enhancement of the temperature profiles. Similar to the changing trends of f'(η) due to γ,θ(η) enhances evidently when γ is small,but when γ grows larger and larger,the effects of γ on θ(η) are smaller and smaller. We further notice that,as γ approaches to 0,θ(η) also diminishes to 0. In this limiting case,the plate is adiabatic so that no heat transfer can be convected through the wall. On the other hand,θ(η) approaches to 1 as γ tends to ∞. In this limiting case,the wall temperature is equal to the temperature of the fluid on the left side of the wall. From this figure,it is also found that the two kinds of the boundary conditions bring minor difference on θ(η). The temperature profiles obtained by the passively controlled model are slightly lower than those given by the actively controlled model.

Figure 4(a) presents the effects of γ on φ(η). The actively controlled model indicates that φ(η) enlarges continuously as γ grows. However,the passively controlled model suggests that φ(η) decreases gradually as γ increases when η < η_c ≈ 0.75. Beyond this value,φ(η) turns to increase along the ascent of γ. This means that the two models give fully different trends of the distributions of nanoparticle concentration for a given value of γ. By the actively controlled model,the concentration of nanoparticles on the wall is always higher than that at the far field. This could be incompatible with experimental results since the slip boundary condition on the surface always holds within nanofluids flow due to the fact that the nanoparticles can hardly be gathered unless external forces are applied. By the passively controlled model,the concentration of nanoparticles on the wall is lower than that at the far field,which provides a good explanation on the slip mechanism of nanofluids on the solid boundary.

The effects of γ on w(η) are illustrated in Fig. 4(b). We notice that the two models generate the similar trend for the variation of w(η) w.r.t. the reduced heat transfer parameter. In both the actively controlled model and the passively controlled model,w(η) enhances smoothly as γ increases. Particularly,when γ is sufficiently large,w(η) increases rapidly to a peak value (which is larger than 1) and then it diminishes to 0 gradually. Also,the appearance of this peak value is delayed as γ continuously grows,and it becomes larger and larger until the maximum value is reached.

We then discuss the effects of various physical parameters on the local skin friction,the local Nusselt number,the local wall mass flux,and the local wall motile microorganisms flux. Note that in the Figs. 5-6,we have taken two of the three parameters Rb,Sc,and Pe fixed and considered the influence of the remaining parameter with the physical quantities,i.e.,while considering the variations of C_fx Re_x^1/2,N_ux Re_x^-1/2,Q_mx Re_x^-1/2,and Q_nx Re_x^-1/2 w.r.t. the individual parameter,the other two are given a constant value of unity. The variations of the reduced local skin friction C_fx Re_x^1/2 caused by the related bioconvection parameters Rb,Sc, and Pe are plotted in Fig. 5(a). It is found that C_fx Re_x^1/2 increases almost linearly as Rb rises according to both two models,but the increase rate given by the passively controlled model is higher than that by the actively controlled model. Physically,Rb measures the ratio between buoyancy and viscosity forces timing the ratio between momentum and thermal diffusivities due to the distributions of microorganisms in the nanofluid,which destabilizes the suspension and accelerates the development of bioconvection. As a result,the skin friction increases as Rb increases. Opposite to the effects of Rb on C_fx Re_x^1/2,the ascent of Sc causes the descent of the reduced local skin friction C_fx Re_x^1/2 by both models. For a given value of Sc,the passively controlled model gives a higher value of C_fx Re_x^1/2 compared with the actively controlled model. Sc characterizes the fluid flows where there are simultaneous momentum and mass diffusion convection processes. The increase in the ratio of the shear component for the diffusivity of viscosity/density to the diffusivity of mass transfer reduces the skin friction on the surface. P_e, which defines the ratio of cell swimming speed to the cell diffusivity,exhibits different roles on the variations of C_fx Re_x^1/2 based on the two models. As P_e enlarges,C_fx Re_x^1/2 increases in the passively controlled model,while in actively controlled model,it decreases. This is due to the reason that in the passively controlled model,the influx of nanoparticles is zero,which is always lower than the actively controlled model,i.e.,Cw is greater than zero. As shown in Fig. 5(b), the variations of N_ux Re_x^-1/2 and Q_mx Re_x^-1/2 along R_b,S_c,and P_e share the same trends to those of C_fx Re_x^1/2 ,as displayed in Figs. 5(b) and 6(a),respectively. It is worth noticing that, for any given value of R_b,S_c and P_e,Q_mx Re_x^-1/2 obtained by the passively controlled model is always higher than the actively controlled model,as presented in Fig. 6(a). The effects of R_b, S_c,and P_e on Q_nx Re_x^-1/2 are given in Fig. 6(b). It is found that for the passively controlled model,Q_nx Re_x^-1/2 increases when either R_b or S_c is enlarged but reduces with the increase of P_e. However,the actively controlled model force Q_nx Re_x^-1/2 increases with the ascent of any of those three parameters.

In practical application,the approximate formulae for the four physical quantities,Re_x^1/2 C_fx,Re_x^-1/2 N_ux,Re_x^-1/2 Q_mx,and Re_x^-1/2 Q_nx,are important,which can be obtained by the linear regression analysis. For example,when

N_r = N_b = N_t = 0.1,G_r= γ = 1,P_r = 6.8,L_e = 10

are prescribed,we are able to obtain their correlations with S_c,P_e,and R_b,i.e.,for the passively controlled model, and for the actively controlled model,

Note that those correlations are obtained by calculating 125 sets of values of Sc,Pe,and Rb in the range of Refs. ^[1,2,3,4,5]. Compared with the numerical results,the relative errors of the results calculated by the above equations (29) to (36) are less than 10% in this given region.

Similarly,we are able to give the correlations of those physical quantities with the controlled nanofluids parameters N_r,N_t,and N_b by means of the linear regression estimation. The correlations of C_fx Re_x^-1/2 with N_r,N_t,and N_b,N_t for different values of Le are listed in Table 1. It is seen that C_fx Re_x^-1/2 increases with N_r and Nt increasing,but decreases with Nb evolving. Similarly,both N_ux Re_x^-1/2 and Q_mx Re_x^-1/2 enhance as Nr and Nt enlarge,but they decrease as N_b increases,as shown in Table 2 and Table 3,respectively. Opposite to the previous trends,Q_nx Re_x^-1/2 reduces as Nr and Nt increase,but increases as N_b evolves, as shown in Table 4. Only the details for the passively controlled model are given here by setting S_b = P_b = R_b = G_r = γ = 1,Pr = 6.8,and taking N_r,N_t,and N_b in the range of [0.1,0.2,0.3,0.4,0.5] with 125 points. As to the actively controlled model,the coefficients and the formulae can be obtained in the similar manner.

The velocity distributions and the isotherms are presented in Fig. 7 that are helpful to make an insight of the physical aspect of this film flow. The temperature of the fluid on the right side of the plate is assumed to be 50°,and the fluid temperature at far field is 15°. In this range,the microoganisms can survive. Since the base fluid is water and the solid particles are copper,the physical properties for the nanofluid are calculated as μf = 1.29 × 10⁻³ kg/(m · s), ρf = 1 800 kg/m³. Substituting those physical quantities into (22) and using ,we get the dimensional velocity and temperature distributions. Also,the film thickness can be calculated via the following formula δ/x = 2ηδ/(3 Re)^1/2,as shown in Table 5. Note that the boundary layer thickness is taken as θ(η) = 0.01 by considering y = δ.

4 Conclusions

We have studied a two-dimensional steady laminar gravity-driven film flow of a nanofluid along a convectively heated vertical wall. The thin film considered in this work contains the mixture of nanoparticles and motile gyrotactic microorganisms. Both the actively and the passively controlled nanofluid models have been tested to investigate this problem. A set of similarity variables have been introduced to reduce the governing partial differential equations to fully coupled nonlinear ordinary differential equations with linear boundary conditions,which have been then solved by a finite difference technique. The results show that the passively controlled nanofluid model is more physically realistic than the actively controlled model,because one cannot control the value of nanoparticle fraction at the boundary in practice,while in the case of passively controlled nanofluid the particle fraction value there adjusts accordingly which can be achieved in practice. The effects of various physical parameters on the profiles of the velocity,the temperature,the nanoparticles concentration,as well as the motile gyrotactic microorganisms are presented and discussed. Furthermore,the correlations of the local skin friction,the local Nusselt number,the local wall mass flux,and the local wall motile microorganisms flux with various physical parameters are established via a linear regression technique.