Shanghai University
Article Information
- M. KHAN, R. MALIK, A. ANJUM. 2015.
- Exact solutions of MHD second Stokes flow of generalized Burgers fluid
- Appl. Math. Mech. -Engl. Ed., 36(2): 211-224
- http://dx.doi.org/10.1007/s10483-015-1906-7
Article History
- Received 2014-3-22;
- in final form 2014-7-27
Considerable progress has been made in studying flows of non-Newtonian fluids over the last few decades. Due to their viscoelastic nature, non-Newtonian fluids, such as oils, paints, ketchup, liquid polymers, and asphalt, exhibit some remarkable phenomena. Increased interest of many researchers has shown that these flows are important in industry, manufacturing of food and paper, polymer processing, and technology. Dissimilar to the Newtonian fluid, the flows of non-Newtonian fluids cannot be explained by a single constitutive model. Therefore, models have been developed for the rheological properties of non-Newtonian fluids.
Amongst them, the rate type fluid model[1] has received great attention. These fluids exhibit the relaxation and retardation phenomena. The Maxwell and Oldroyd-B fluids are amongst the simplest types of such fluids. Finding analytical solutions is quite difficult for such fluids. In spite of several challenges, many researchers have established the analytical solutions regarding these fluids.The exact solution that has beeninvestigated by Fetecau et al. [2] takes into account the flow of Oldroyd-B fluid, which is due to the constantly accelerating flat plate placed between two perpendicular side walls. Fetecau et al. [3] scrutinized the helical flows of Oldroyd-B fluids. Tan et al. [4] scrutinized the exact solution for the flow of the fractional Maxwell model induced by impulsive motion of a plate, when the fluid is placed between two parallel plates. Li et al. [5] presented the exact solution of the problem of helical flows while taking heated generalized Oldroyd-B fluid in a porous medium. Analytical solutions were determined for the Oldroyd-B fluid caused by oscillations of an infinite flat plate, oscillating pressure gradient and pressure jumps by Aksel et al. [6] . Unsteady flow of a generalized Oldroyd-B fluid under the influence of uniform magnetic field was investigated by Zheng et al. [7] .Vieruetal.[8] examined the flow of the generalized Oldroyd-B fluid, taking place due to the plate which is accelerating constantly. Stokes’ first problem combined with modified Darcy’s law was analyzed by Tan and Masuoka[9] . Exact solution for the magnetohydrodynamic (MHD) flows of an Oldroyd-B fluid passing through a porous space was investigated by Khan et al. [10] . However, these models cannot predict the rheological properties of some food products like cheese. In 1935, onedimensional rate type fluid model which is named as the Burgers model [11] was considered in the thermodynamic framework. Later, this work was extended by Krishnan and Rajagopal [12] for three-dimensional flow. The Burgers fluid model is used to explore the properties of earth mantle. This model is also used to describe the behavior of asphalt concrete[13] . In addition, the Burgers model is sometimes used to describe other geological structures, such as Olivine rocks [14] and the propagation of seismic waves in the interior of the earth [15] . Here, we cite some studies [16, 17, 18, 19, 20] related to the Burgers fluid. Moreover, MHD flow involving such fluids has promising applications related to the development of energy generation, astrophysics, and geophysics fluid dynamics. Recently, the theory of MHD has received great attention (see Refs. [21, 22] and the references therein). The effects of transverse magnetic field in the porous space over the unsteady non-Newtonian fluids were analyzed by several researchers [23, 24, 25, 26] .
Motivated by the above mentioned studies, this work presents an MHD flow of the generalized Burgers fluid passing through a porous medium due to the oscillation of an infinite rigid plate. The influence of transverse magnetic field and modified Darcy’s law on the flow is considered. The resulting expressions of velocity distribution and shear stress can be described as a combination of steady-state and transient solutions. The effects of various physical parameters are discussed through graphical illustrations. 2 Problem formulation
The Cauchy stress tensor T in the generalized Burgers fluid is defined by [16, 17, 18, 19, 20]
where S denotes extra-stress tensor, p denotes the pressure, I denotes the identity tensor, μ denotes the dynamic viscosity, A1 = L + LT denotes the first Rivlin-Ericksen tensor with L as the gradient of velocity, λ1 and λ3( ≤ λ1) represent time of relaxation and retardation, respectively, λ2 and λ4 represent generalized Burgersfluid material parameters, and δ/δt represents the upper convected time derivative defined as in which d/dt represents the material time derivative.The governing equations for unsteady flow of incompressible fluid are expressed as follows:
where V denotes the velocity, ρ represents the fluid density, σ represents the electrical conductivity of the fluid, Rdenotes Darcy’s resistance, and B0 represents the magnitude of applied magnetic field, whereas the induced magnetic field is ignored by choosing a small magnetic Reynolds number[7].Velocity and stress fields for the flow analysis are expressed as follows:
where i represents the unit vector in the direction of x. The velocity field (5) automatically satisfies the continuity equation (3).Substitute (5) into (1), and use the initial conditions
which yields Syy = Syz = Szz = Sxz = 0 and where Sxy is the tangential stress.In view of Ref. [22], we have the following relation ofRfor a generalized Burgers fluid:
where k represents porous medium permeability, and φ represents the porosity.By substituting (5) into (4), with (7) and (8) and in the absence of pressure gradient in the flow direction, the governing equation becomes
where ν(=μ/ρ) represents the kinematic viscosity of the fluid. 3 Geometry of problemThe physical model under consideration with the coordinate system is shown in Fig. 1.
 |
| Fig. 1 Physical model under consideration with coordinate system |
Let us consider an incompressible and electrically conducting generalized Burgers fluid. The fluid occupies the porous space above the flat plate perpendicular to they-axis and permeated by an applied magnetic field B0 normal to the flow. The plate starts to oscillate with velocit y UH(t) cos(wt) or UH(t) sin(wt) with H(·)for t > 0 as the Heaviside unit step function and U as the amplitude of plate velocity. Fluid particles move above the plate due to shear stress. The governing equation of the problem is (9) with the associated initial and boundary conditions
In the non-dimensional form, we can write the above problem as and the asterisks have been omitted for simplicity. 4.1 Calculation of velocity fieldIn order to obtain the exact solution related to the flow for both small and large times, Fourier sine and Laplace transforms [27] are used. Thus, multiplying (13) by sin(yξ)onboth sides, integrating the resulting expression with respect to yfrom 0 to infinity, and utilizing (14)-(16), we find that
while the initial conditions take the form Applying the Laplace transform on (18) and (19) subject to the (20), we obtain where Us(ξ, r) represents the Laplace transform of us(ξ, t), rrepresents the transform parameter, and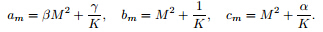
Rewrite (21) and (22) in a simpler form as
where (24) and (25) can also be written as where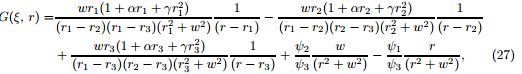
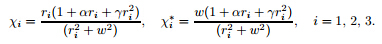
The starting solutions, i.e., (33) and (34) are expressed as a combination of the steady-state and transient solutions. The steady-state solutions are
4.2 Calculation of shear stressTo compute the shear stress, we use the relation (7) in the non-dimensional form as follows:
The Laplace transform reduces (37) to the following form: where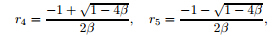
Substituting (39) and (40) into (38), we reach at the following expressions:
or in a simpler form, we can write as whereInverting (43) by means of the Laplace transform and following the same way as for the velocity field, we find the following expressions for the tangential stress:
where we have used notations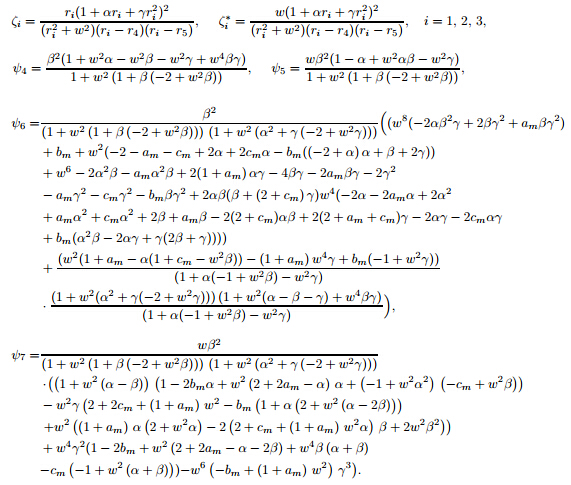
To study the significant physical effects of the obtained results, the impact of the material parameters on the fluid motion is highlighted by graphical illustration of the velocity profiles for the flow due to the sinusoidal oscillations of the infinite plate. To illustrate the difference, we depict the velocity profile for both cases, i.e., cosine oscillations and sine oscillations. The numerical results are plotted for various values of timet, M, permeability parameter K, and the rheological parametersβandγof Burgers and generalized Burgers fluids.
Figure 2 compares the velocity profiles for various values of time for cosine as well as sine oscillations of the boundary, respectively. It is noted that similar amplitudes and a phase shift persevere for all times in the case of cosine as well as sine oscillations. Here, we can observe that as the bottom plate is set into motion, the velocity near the bottom plate is developing and fluctuating around zero with the same frequency as the plate. Additionally, the fluid oscillation has maximum amplitude adjacent to the plate at y = 0 and reduces far away from the plate and approaches zero.
 |
| Fig. 2 Velocity profileu(y, t) given by (33) and (34) for various values of timetfor cosine and sine oscillations of boundary, respectively |
Figure 3 presents the profiles of the velocity for various values of the magnetic parameter M for both cosine as well as sine oscillations of the boundary, respectively. Since magnetic field is applied in the transverse direction, it is a force which resists the flow. Therefore, by increasing the value ofM, the amplitude of the oscillation tends to decrease. Also, it is scrutinized that the amplitude of oscillation is larger for the hydrodynamic case (M = 0) when compared with the hydromagnetic case (M ≠ 0). The effects of the permeability parameterKare depicted in Fig. 4. It has quite opposite effect on the velocity profile compared with that of the magnetic parameterM. It is noted that with the increasing Kthe velocity field increases.
 |
| Fig. 3 Velocity profileu(y, t) given by (33) and (34) for various values of Mfor cosine and sine oscillations of boundary, respectively |
 |
| Fig. 4 Velocity profileu(y, t) given by (33) and (34) for various values of Kfor cosine and sine oscillations of boundary, respectively |
Figure 5 presents the effect of material parameter β onthevelocityprofileforbothcosine as well as sine oscillations of the boundary, respectively. We can clearly see from the figure that the velocity decreases slightly by increasing the parameter β.Further, the effect of the rheological parameter γof the generalized Burgers fluid is shown in Fig. 6 for cosine as well as sine oscillations of the boundary, respectively. It is noted that an increase in the rheological parameterγof generalized Burgers fluid yields an effect opposite to that of the parameter β. From these figures, it is noticed that the profile of the velocity for the sine oscillation is more sensitive compared with the cosine oscillations of the boundary. Additionally, Fig. 7 delineates the influence of the magnetic parameterMon the shear stress. It is quite clear from this figure that for the larger values of M, the magnitude of shear stress decreases for both cosine as well as sine oscillations. Also, we can compare the hydromagnetic (M ≠ 0) and hydrodynamic (M = 0) cases. It might be seen from this figure that the amplitude of oscillation is larger for the later case.
 |
| Fig. 5 Velocity profileu(y, t) given by (33) and (34) for various values of βfor cosine and sine oscillations of boundary, respectively |
 |
| Fig. 6 Velocity profileu(y, t) given by (33) and (34) for various values of γfor cosine and sine oscillations of boundary, respectively |
 |
| Fig. 7 Profile of tangential stress τ(y, t) given by (46) and (47) for various values of Mfor cosine and sine oscillations of boundary, respectively |
In this article, the problem of an MHD flow through a porous medium involving generalized Burgers fluid has been discussed for two types of oscillations of the plate, i.e., cosine and sine oscillations. The governing equations are modeled by employing the modified Darcy’s law developed for the generalized Burgers fluid. Combined Fourier sine and Laplace transforms are employed to construct the results for the flow. These results, expressed as a combination of the steady-state and transient parts, explain the flow of the fluid after some time of the initiation. After some time, when the transient solutions vanish, the motion of the fluid is called steadystate, which does not depend on initial conditions. Considering the derived results, we have analyzed the influence of the various parameters on velocity profile of the fluid. The obtained results indicate that
(I) With the increase in the magnetic parameter M, the magnitude of velocity distribution is decreased, while the opposite effect could be seen for permeability parameter K for cosine as well as sine oscillations.
(II) For cosine as well as sine oscillations, the magnitude of velocity profile is decreased with the increasing value of the material parameter β, whereas quite opposite behavior might be seen for the rheological parameter γ.
(III) The magnitude of the shear stress is decreased for larger values of M for both cosine and sine oscillations.
| [1] | Rajagopal, K. R. Mechanics of non-Newtonian fluids. Recent Development in Theoretical Fluids Mechanics, Pitman Research Notes in Mathematics, Longman, New York, 129-162 (1993) |
| [2] | Fetecau, C., Hayat, T., Khan, M., and Fetecau, C. Unsteady flow of an Oldroyd-B fluid induced by the impulsive motion of a plate between two side walls perpendicular to the plate. Acta Mechanica, 198, 21-33 (2008) |
| [3] | Fetecau, C., Fetecau, C., and Vieru, D. On some helical flows of Oldroyd-B fluids. Acta Mechanica, 189, 53-63 (2007) |
| [4] | Tan, W. C., Pan, W., and Xu, M. Y. A note on unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates. International Journal of Non-Linear Mechanics, 38, 645-650 (2003) |
| [5] | Li, C., Zheng, L., Zhang, Y., Ma, L., and Zhang, X. Helical flows of a heated generalized Oldroyd- B fluid subject to a time-dependent shear stress in porous medium. Communications in Nonlinear Science and Numerical Simulation, 17, 5026-5041 (2012) |
| [6] | Aksel, N., Fetecau, C., and Scholle, M., Starting solutions for some unsteady unidirectional flows of Oldroyd-B fluids. Zeitschrift für Angewandte Mathematik und Physik, 57, 815-831 (2006) |
| [7] | Zheng, L., Liu, Y., and Zhang, X., Slip effects on MHD flow of a generalized Oldroyd-B fluid with fractional derivative. Nonlinear Analysis: Real World Applications, 13, 513-523 (2012) |
| [8] | Vieru, D., Fetecau, C., and Fetecau, C. Flow of a generalized Oldroyd-B fluid due to a constantly accelerating plate. Applied Mathematics and Computation, 201, 834-842 (2008) |
| [9] | Tan, W. C. and Masuoka, T. Stokes first problem for an Oldroyd-B fluid in a porous half space. Physics of Fluids, 17, 023101 (2005) |
| [10] | Khan, M., Khan, S. B., and Hayat, T. Exact solution for the magnetohydrodynamic flows of an Oldroyd-B fluid through a porous medium. Journal of Porous Media, 10, 391-399 (2007) |
| [11] | Burgers, J. M. Mechanical considerations-model system-phenomenological theories of relaxation and of viscosity. First Report on Viscosity and Plasticity (ed. Burgers, J. M.), Nordemann Publishing Company, New York (1935) |
| [12] | Krishnan, J. M. and Rajagopal, K. R. A thermodynamic framework for the constitutive modeling of asphalt concrete: theory and application. Journal of Materials in Civil Engineering, 16, 155-166 (2004) |
| [13] | Lee, A. R. and Markwick, A. H. D. The mechanical properties of bituminous surfacing materials under constant stress. Journal of the Indian Chemical Society, 56, 146-156 (1937) |
| [14] | Tan, B. H., Jackson, I., and Gerald, J. D. F. High-temperature viscoelasticity of fine-grained polycrystalline olivine. Physics and Chemistry of Minerals, 28, 641-664 (2001) |
| [15] | Peltier, W. R., Wu, P., and Yuen, D. A. The viscosities of the Earth mantle. Anelasticity in the Earth (eds. Stacey, F. D., Paterson, M. S., and qicholas, A.), American Geodynamics Series, American Geophysical Union, Washington, D. C. (1981) |
| [16] | Hayat, T., Khan, S. B., and Khan, M., Influence of Hall current on the rotating flow of a Burgers’ fluid through a porous space. Journal of Porous Media, 11, 277-287 (2008) |
| [17] | Hayat, T., Hussain, M., and Khan, M. Effect of Hall current on flows of a Burgers’ fluid through a porous medium. Transport in Porous Media, 68, 249-263 (2007) |
| [18] | Khan, M., Ali, S. H., and Fetecau, C. Exact solutions of accelerated flows for a Burgers’ fluid, I, the case γ < λ2/4. Applied Mathematics and Computation, 203, 881-894 (2008) |
| [19] | Hayat, T., Fetecau, C., and Asghar, S. Some simple flows of a Burgers’ fluid. International Journal of Engineering Science, 40, 1423-1431 (2006) |
| [20] | Ravindran, P., Krishnan, J. M., and Rajagopal, K. R. A note on the flow of a Burgers’ fluid in an orthogonal rheometer. International Journal of Engineering Science, 42, 1973-1985 (2004) |
| [21] | Hayat, T. and Sajid, M. Homotopy analysis of MHD boundary layer flow of an upper-convected Maxwell fluid. International Journal of Engineering Science, 45, 393-401 (2007) |
| [22] | Khan, M., Hayat, T., and Asghar, S. Exact solutions of MHD flow of a generalized Oldroyd-B fluid with modified Darcy’s law. International Journal of Engineering Science, 44, 333-339 (2006) |
| [23] | Khan, M., Ali, S. H., Fetecau, C., and Hayat, T. MHD flows of a second grade fluid between two side walls perpendicular to a plate through a porous medium. International Journal of Non-Linear Mechanics, 43, 302-319 (2008) |
| [24] | Hayat, T., Khan, S. B., and Khan, M. Exact solution for rotating flows of a generalized Burgers’ fluid in a porous space. Applied Mathematical Modelling, 32, 749-760 (2008) |
| [25] | Hayat, T., Khan, M., and Asghar, S. On the MHD flow of fractional generalized Burgers’ fluid with modified Darcy’s law. Acta Mechanica Sinica, 23, 257-261 (2007) |
| [26] | Ali, F., Norzieha, M., Sharidan, S., Khan, I., and Hayat, T. New exact solutions of Stokes’ second problem for an MHD second grade fluid in a porous space. International Journal of Non-Linear Mechanics, 47, 521-525 (2012) |
| [27] | Snedden, I. N. Fourier Transforms, McGraw Hill Book Company, New York (1951) |
 2015, Vol. 36
2015, Vol. 36




























