Shanghai University
Article Information
- Fan YANG, Yajun YIN, Bin HE, Qinshan FAN. 2015.
- Fractal growth kinematics abstracted from snowflakes: topological evolution
- Appl. Math. Mech. -Engl. Ed., 36(2): 243-264
- http://dx.doi.org/10.1007/s10483-015-1903-7
Article History
- Received 2014-5-28;
- in final form 2014-6-18
2. Division of Mechanics, Nanjing University of Technology, Nanjing 211816, China
In scientific experiments,surprising phenomena often occur. Figure 1 is a transmembrane protein named bacteriorhodopsin[1]. Figure 2 is the self-assembly pattern of CoFe2O4 nanocrystals[2]. Figure 3 is the micro-structures of surfaces on polymer alloy particles[3]. These phenomena belong to different disciplines,but they present surprising common properties: the patterns with six-axis-symmetry and the multilevel structures with self-similarity. In short,all of them are six-axis-symmetric patterns with fractal characteristics.
In nature,snowflakes (see Fig. 4) are also six-axis-symmetric patterns with fractal characteristics. Therefore,all of six-axis-symmetric patterns with fractal characters are uniformly called the snowflake-like fractal patterns.
 |
| Fig. 1. Bacteriorhodopsin and transmembrane protein[1] |
 |
| Fig. 2. Self-assembly pattern of CoFe2O4 nano-crystals[2] |
 |
| Fig. 3. Geometrical pattern of surfaces on polymer alloy particles[3] |
 |
| Fig. 4. Snowflake in nature |
The snowflake-like fractal patterns also exist in geometry. Recently,graceful fractal
patterns[4, 5, 6, 7, 8, 9, 10, 11] have been constructed. One of them is the fractal snowflake,whose initial cell
element is a circular disk or hexagon (see Fig. 5),and the self-similar ratio is rs =  . Figures 6 and 7 present the growth processes of the close-packed and the dispersive fractal snowflakes,
respectively.
. Figures 6 and 7 present the growth processes of the close-packed and the dispersive fractal snowflakes,
respectively.
 |
| Fig. 5. Initial circular disk cell element |
 |
| Fig. 6. Close-packed fractal snowflake[6] |
 |
| Fig. 7. Dispersive fractal snowflake[9] |
Fractal snowflakes are similar to the actual patterns: in Fig. 6,the second level structure generally conforms to the patterns in Figs. 1 and 2. The second level structure of Fig. 7 coincides with the patterns in Figs. 3 and 4. These phenomena inspire us that the growth dynamics of snowflake-like fractal patterns is different but their growth kinematics may be identical. Nevertheless,during the study of growth kinematics,contradictions arise gradually. To resolve them,the breakthrough on concepts is necessary,which forms the motivation of this paper.
The contents in this paper are as follows: (i) The confusions in fractal snowflakes are represented and the contradictions between fractal snowflakes and classical fractal modes are exposed. (ii) Based on the kinematic viewpoint,several concepts,i.e.,the proportional movement and the transformation group for proportional movement,are defined. (iii) The necessary and sufficient conditions for the self-similarity of multilevel geometric structures are proposed under the transformation group for proportional movement. (iv) Based on proportional movement, the characteristic topology is abstracted from fractal snowflakes. The identity between the characteristic topology of snowflake-like fractal and the topology of ternary-segment fractal line is proved. (v) The formulations of the characteristic gaps of N-segment line under the proportional movement transformation groups are revealed. (vi) Based on characteristic gaps,the growth conditions and the infinite growth conditions of N-segment line are derived. (vii) The proposition that the topological evolution of the N-segment line is mainly controlled by the topological invariant N is verified. 2 Confusions caused by fractal snowflakes
The first confusion is the contradiction between the growth modes of fractal snowflakes and classical modes. There are two common growth modes in the classical regular fractals. One is the “chiseling inward” mode,i.e.,continuous inward chiseling (e.g.,the Sierpinski gasket). Another is the “growing outward” mode,i.e.,continuous outward growing (e.g.,the Koch curve). Obviously,the close-packed fractal snowflake in Fig. 6 follows the “chiseling inward” mode.
Nonetheless,the fractal snowflake in Fig. 7 is very weird. It looks like the “chiseling inward” mode,but does not strictly comply with the rules. It is similar to the “growing outward” mode,but does not meet the requirements. In other words,it cannot be attributed to the growth modes of regular fractal sets.
The second confusion is the disappearance of the self-similarity. The fractal snowflake in Fig. 7 satisfies the self-similarity strictly. However,if some conditions are broken,amazing result often occurs: the self-similarity is absent (see Fig. 8),i.e.,the similarity between the part and the whole does not exist.
 |
| Fig. 8. Dissimilar snowflake-like multilevel structure |
The third confusion is the connective phenomena of fractal snowflakes. Figure 7 displays novel topological properties. Along with the increase of the structure level number,adjacent circular disks move towards each other gradually. When the level number tends to infinity,all adjacent points in fractal set tend to connect locally and globally at the same time. These phenomena are so rare that we have believed that the fractal snowflake in Fig. 7 is unique. However,once Fig. 9 appears,this opinion is overruled. In Fig. 9,another piece of fractal snowflake “tending to connection simultaneously” is born magically after infinite circulations.
 |
| Fig. 9. Another dispersive fractal snowflake |
Surprising phenomena occur successively. Noticeably,the above fractal snowflakes are infinite levels structures. Nevertheless,if parameters have tiny change,wonderful patterns appear. As shown in Fig. 10,when the self-similar snowflake grows to the fourth level,adjacent circular disks connect with each other and block the growing space.
 |
| Fig. 10. Dispersive fractal snowflake of finite growth |
To resolve contradictions,we should break through convention. Our strategy is to abstract more universal growth modes and refine more general geometric concepts from fractal snowflakes. 3.1 Concept of proportional movement
More general geometric concept mentioned above is the “proportional movement”. From
the kinematic viewpoint,the growing process of fractal snowflakes is the process of movements.
Two sorts of basic movements are included. One is the compressive movement: the initial
circular disk with diameter d0 is centrally compressed to a smaller circular disk with diameter
d1 = d0 (see Fig. 11). The other is the translational movement: the central smaller circular
disk remains fixed,and other six copies move along six-axial-symmetric (radial) directions with
their centers located on the contour line of the circular element (the translational distance of
circular center is D1 = 2d1) to form the (6 + 1) pattern of the 1st level structure (see Fig. 7).
Then,with the fixed ratio
d0 (see Fig. 11). The other is the translational movement: the central smaller circular
disk remains fixed,and other six copies move along six-axial-symmetric (radial) directions with
their centers located on the contour line of the circular element (the translational distance of
circular center is D1 = 2d1) to form the (6 + 1) pattern of the 1st level structure (see Fig. 7).
Then,with the fixed ratio  ,the 2nd level structure formed by smaller circles with diameter
d2 =
,the 2nd level structure formed by smaller circles with diameter
d2 =  d1 and the translational distance of circular centers D2 =
d1 and the translational distance of circular centers D2 =  D1 may be obtained. After
infinite repetitions,the dispersive fractal snowflake is obtained (see Fig. 7).
D1 may be obtained. After
infinite repetitions,the dispersive fractal snowflake is obtained (see Fig. 7).
 |
| Fig. 11. Proportional growth movement of dispersive fractal snowflake |
Two sorts of basic movement mentioned above have the following properties: (a) “Compressive
movement/translational movement” appears alternately to form a circulation. (b) Each
circulation generates one level structure of fractal snowflakes. (c) The compressive movement
sequence and the translational movement sequence have their own corresponding ratios. Accordingly,
the proportional movement of fractal snowflakes can be defined as follows: both for
the compressive movement sequence and for the translational movement sequence,the characteristic
metric ratios are all the constant value  ,i.e.,
,i.e.,
Corresponding to the proportional movement mode,the transformation group for proportional movement may be defined.
There is natural relevance between the proportional movement and basic transformations (or mappings) in mathematics. There are several basic transformations in mathematics,i.e., compressive transformation,translational transformation,rotational transformation,reflective transformation. Among them,compressive transformation and translational transformation refer to metric ratios. Both of them correspond to proportional movements: the central compressive movement corresponds to compressive transformation and the radial translational movement is according to translational transformation.
The above corresponding relationship will be expanded further. In mechanics,the circulation of “compressive movement/translational movement” forms two movement sequences and generates multilevel structures. In mathematics,the circulation of “compressive transformation/ translational transformation” produces two transformation sequences and constructs two transformation groups. If these two transformation groups satisfy the following conditions, they are proportional movement transformation groups. The compressive movement sequence satisfies that the characteristic metric ratio between two adjacent structures is constant,i.e.,
The translational movement sequence satisfies that the ratio of the translational distance between two adjacent structures is constant,i.e., Here,rs(1) is the self-similar ratio of the proportional compressive movement and rs(2) is the self-similar ratio of the proportional translational movement. Obviously,(2a) and (2b) are the extensions of (1a) and (1b),respectively. 3.3 Universality of proportional movementsThough the concept of the proportional movement is defined to illustrate the dispersive fractal snowflakes,it is of universality. Figure 12 is the close-packed fractal snowflake described by proportional movement. Figure 13 is the Sierpinski gasket formed by proportional movement.
 |
| Fig. 12. Close-packed fractal snowflake described by proportional growth movement |
 |
| Fig. 13. Proportional growth movement of Sierpinski gasket |
Because the concept of proportional movement is of universality,it creates a universal proportional movement mode. The task of the proportional growth kinematics is to study the invariant properties of multilevel structures under proportional movement transformation groups. 4 Proportional movement transformation groups and self-similarity
One invariant property is the self-similarity. Based on proportional movement transformation groups,a question may be answered: how do we ensure the self-similarity of a multilevel structure?
To display the essence of the problem,we construct a simplest multilevel structure,the binary-segment line,through proportional movement transformation groups and by imitating the growth of fractal snowflakes in Fig. 7. Its forming process is as follows.
First,through compressive transformation,the initial segment with length d0 (the 0th level structure) is centrally and symmetrically compressed to a shorter segment with length d1 = rs(1)d0. Second,after copying in situ,through translational transformation,the centers of two segments with length d1 are translated the distance D1 leftward and rightward respectively to obtain the 1st level structure. Then,through proportional movement mode,the 2nd level structure formed by shorter segment with length d2 = rs(1)d1 and the translational distance D2 = rs(2)D1 may be obtained. Finally,after infinite repetitions,the binary-segment line (see Fig. 14) is obtained.
 |
| Fig. 14. Binary-segment line formed by proportional movement |
Under what condition the binary-segment line in Fig. 14 is of self-similarity? If binarysegment line is of self-similarity,it needs to satisfy the following statements:
(a) The apparent characteristic metric remains similarity,and the ratio of the characteristic length is constant (see Fig. 15),i.e.,

 |
| Fig. 15. Necessary and sufficient conditions for self-similarity |
(b) The topological characteristic metric remains similarity,i.e.,the ratio of characteristic length of gaps between two line segments is constant (see Fig. 15),i.e.,

(c) These two constant ratios must be identical. Then,we have
From (3),we obtain (4) showsIn other words,self-similar binary-segment line must meet rs(1) = rs(2). It is easy to prove that this condition is both sufficient and necessary.
From the analysis we can summarize the proposition.
Proposition 1 Under the transformation groups for proportional movement,the necessary and sufficient condition for the self-similarity of the binary-segment line is rs(1) = rs(2).
This proposition can be expanded to common geometric structures. For convenience,the concept of similar transformation group for proportional movement is introduced: two proportional movement transformation groups are similar,if they satisfy rs(1) = rs(2). Hereof,we have a general proposition.
Proposition 2 The necessary and sufficient condition for a multilevel structure to be selfsimilar is that the two transformation groups for proportional movement are similar.
This proposition explains the confusion phenomena: the snowflake-like patterns in Fig. 8 are formed by two proportional movement transformation groups,because these two groups are dissimilar,i.e.,rs(1) ≠ rs(2),thus the patterns are not self-similar. 5 Topological evolution of N-segment line under proportional movement translational groups
Now we focus on the third confusion question: are the two fractal snowflakes in Figs. 7 and 9 identical? This question leads to a series of questions: is the “simultaneous connection” an isolate example or a universal existence? If it is a universal existence,then under what condition “simultaneous connection” can occur? If the “connection” is regarded as the critical condition for stopping growth,then why some self-similar structures can grow infinite levels while some can only grow finite levels? What is the condition that determines the infinite growth?
All the above questions are related to a keyword: topological connection. “Connection” is a phenomenon that exists universally and possesses essential importance. In mathematics, “connection” is the core subject in topology. In physics and mechanics,“connection” means mutation of properties. In nature,the connection of finite level structures is very common. How do we study these phenomena quantitatively? The answer can be found in the following sections. 5.1 From fractal snowflakes to ternary-segment line
In this section,the fractal snowflake is still taken as a typical example. Such proposition will be proved.
Proposition 3 Under proportional movement transformation groups,the characteristic topology of snowflake-like fractal patterns is identical to the topology of the ternary-segment fractal line.
For convenience,three terms,i.e.,“the characteristic intersection”,“the characteristic pattern”, and “the characteristic topology” are introduced. A plane intersecting with a multilevel structure may cut a pattern. The characteristic intersection is such a plane that the pattern cut from the multilevel structure maintains entire characteristic topological properties of the original multilevel structure. The pattern intersected by the characteristic intersection is called the characteristic pattern. The topology of the characteristic pattern is called the characteristic topology of the original multilevel structure.
Now we examine the concepts above through fractal snowflakes. A fractal snowflake in the 2D plane has six symmetric axes. Among them,three pass through the most circular disks and may be called “the principal symmetric axes”. For the restrictions of the symmetry and the proportional movement mode,the characteristic topological information of fractal snowflake is mapped invariably onto the principal symmetric axes. The reasons are as follows. In Fig. 16, O0O1 and O0O'1 are half axes of two principal symmetric axes,respectively. Thus,the pattern on the O0O1 and the pattern on the O0O'1 must be identical. Although O1O'1 is not principal symmetric axis,the pattern on it is also identical to the patterns on the O0O1 and O0O'1. Therefore,if the pattern on one principal symmetric axis is clarified,then the patterns of the fractal snowflakes are determined completely.
 |
| Fig. 16. Topological mapping from fractal snowflake to principal symmetric axes |
The characteristic intersection of the fractal snowflakes is the plane perpendicular to the plane of snowflake and through a principal symmetric axis. The intersected pattern is the ternary-segment fractal on the principal symmetric axes. Take Fig. 17 as an example to display the growth sequence of its characteristic pattern. There is 1 segment on the symmetric axis of the 0th level structure (the circular cell element in Fig. 17(a)). There are 3 segments on a principal symmetric axis of the 1st level structure (see Fig. 17(b)). There are 32 segments on a principal symmetric axis of the 2nd level structure (see Fig. 17(c)). · · ·. There are 3i segments on a principal symmetric axis of the ith level structure. When i→∞,the characteristic pattern of the fractal snowflake — the ternary-segment fractal is obtained (see Fig. 17(e)).
 |
| Fig. 17. Characteristic fractal pattern of fractal snowflake |
For the characteristic topology of the fractal snowflake is identical to the topology of the ternary-segment fractal,once the topological evolution law of the latter is clarified,then the topological evolution law of the former is clear completely,i.e.,by means of characteristic topology,the complex movement of fractal snowflakes may be equivalently transformed to the simple movement of the ternary-segment fractal. Then,by the quantitative description of the simple movement,the analytic depiction of the complex movement may be achieved. 5.2 Concept of characteristic gaps
The concept of “characteristic gaps” may be traced back to Ref. [9]. The “minimal distance” inside fractal snowflakes,which means the straight distance between a pair of closest points in adjacent small circular disks,was defined in Ref. [9]. Now the “minimal distance” is expanded to multilevel structures: the minimal distance between adjacent sub-structures is called the “characteristic gap”,marked by g(i,j) (see Fig. 18). Here,the index i represents the ith level structure,and the index j represents the jth level sub-structure (1 ≤ j ≤ i). Then,g(i,j) means the minimal distance or gap between the jth level sub-structures in the ith level structure.
 |
| Fig. 18. Characteristic gaps of fractal snowflake |
First,we observe the snowflake-like multilevel structures (see Fig. 18). In the 1st level structure,there is only the 1st level sub-structure,i.e.,the seven small circular disks have minimal distance g(1,1). In the 2nd level structure,there are two levels sub-structures. Here, the 1st level sub-structure is seven datum line circles with the minimal distance g(2,1),and the 2nd level sub-structure is seven small circular disks on every datum line circle with the minimal distance g(2,2). Successively,g(i,j) for the snowflake-shape multilevel structures may be obtained.
Second,we observe the ternary-segment line (see Fig. 19). In the 1st level structure,there is only the 1st level sub-structure including a left segment,a middle segment,and a right segment with the minimal distance g(1,1). In the 2nd level structure,there are two level sub-structures. The 1st level sub-structure includes three segments on the left side,three segments on the middle and three segments on the right side with minimal distance g(2,1). The 2nd level substructure is every short segment with three segments on the left,middle,and right sides with minimal distance g(2,2). Successively,g(i,j) for the ternary-segment line may be obtained.
 |
| Fig. 19. Characteristic gaps of ternary-segment line |
In order to ensure the universality of results,we study the topological evolution of N-segment line directly in this section. Under proportional movement transformation groups,the growth process of N-segment line is as follows.
Suppose the length of the initial segment is d0. First,the initial segment d0 is compressed symmetrically around the center to a shorter segment with length d1 = rs(1)d0. Second,the shorter segment d1 is copied N times in situ. Then,these N copies are translated relatively to the symmetrical center leftward and rightward,and distributed periodically with the central distance D1 between two adjacent shorter segments. Thus,the 1st level structure is formed. Third,according to the proportional movement mode,the 2nd level structure is formed,in which the shorter segments have length d2 = rs(1)d1,and the central distance between two adjacent segments is D2 = rs(2)D1. Finally,after infinite circulation,the N-segment line (see Fig. 20) is obtained.
 |
| Fig. 20. N-segment line (take 5th-segment line as example) |
Characteristic gaps of the N-segment line are also marked by g(i,j) (see Fig. 21). By means of proportional movement transformation groups,g(i,j) can be derived quantitatively. In the 1st level structure,we have
 |
| Fig. 21. Characteristic gaps in N-segment line (take 5th-segment line as example) |
In the 2nd level structure,we have
In the 3rd level structure,we have
Successively,in the ith level structure,we have
(6d) can be written in a unified form as follows:The dimensionless form of (7) is made by d0,i.e.,

Both sides of (7) are divided by d0 as follows:
If let N = 3,(8a) will degenerate to the gap evolution law for the ternary-segment line or snowflake-like patterns as follows: 5.4 Topological invariant in gap evolution(8a) displays the restrictive factors of topological evolution: four parameters rs(1),rs(2),rd, and N as well as two variables,i.e.,the structural level number i and the sub-structural level number j.
In (8a),N is an invariant that describes the topological characteristic of N-segment line, and may be called topological invariant. 5.5 Topological invariant and infinite growth conditions
Based on g(i,j),a few concepts may be defined. For the given i and j,if g(i,j) = 0,then it is said that connection occurs in the multilevel structure. If g(i,j) < 0,it is said that overlapping happens in the multilevel structure. If g(i,j) = 0 or g(i,j) < 0 happens at finite level number i, it is said that finite growth is met in the multilevel structure.
If g(i,j) ≥ 0 is valid for any level number i,it is said that infinite growth is realized in the
multilevel structure. As infinite level is reached without obstacles,the infinite growth is also
called the free growth. If  = 0 is satisfied simultaneously,it is said that “simultaneous
connection at limit state” happens in the multilevel structure.
= 0 is satisfied simultaneously,it is said that “simultaneous
connection at limit state” happens in the multilevel structure.
The solution of g(i,j) ≥ 0 is that free growth conditions for the N-segment line. However, g(i,j) ≥ 0 is a nonlinear inequality with high order that is difficult to solve directly. Therefore, we try to find a simple way to derive the free growth conditions.
From N-segment line in Fig. 21,we can find that the free growth must satisfy two necessary conditions. The first necessary condition is summarized as follows,i.e.,between the ith level sub-structures in the ith level structure (see Fig. 21),the gaps must exist. Concretely speaking, between the 1st level sub-structures in the 1st level structure,we should have
Between the 2nd level sub-structures in the 2nd level structure,we should have Successively,between the ith level sub-structures in the ith level structure,we should haveThe inequality (9c) can be further written as
For rs(1) > 0,there is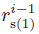 > 0. Both sides of the inequality (10) are divided by
> 0. Both sides of the inequality (10) are divided by 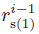 D1 as
D1 as
Notably,every level structure should satisfy the inequality (11). Two extreme states will be considered below. One is that when i→∞,the inequality (11) must be valid,
Another is that when i = 1,the inequality (11) must be valid. In this case,the inequality (11) degrades to the inequality (9a). Both sides of (9a) are divided by d0 as follows:
Obviously,the inequality (13) is the precondition for the first level structure to grow from the cell element.
As long as the inequality (11) is valid at two extreme states,then it is valid identically
for arbitrary structural level number i. The reason is as follows. Let a =  . For a > 1,
f(x) = ax is an increasing function of x. Hereby,if f(1) ≥
. For a > 1,
f(x) = ax is an increasing function of x. Hereby,if f(1) ≥  ,for arbitrary x > 1,there must be f(x) ≥
,for arbitrary x > 1,there must be f(x) ≥  .
.
The second necessary condition is summarized as follows: between the ith level sub-structures in the ith level structure (see Fig. 21),the gaps not only exist,but also are large enough so as to contain the growth of succeeding level structures. Concretely speaking,between the 1st level sub-structures in the 1st level structure,the distance D1 must be large enough,only when D1 satisfies the inequality below,more than two levels structure can be contained (see Fig. 21),
Similarly,the distance D2 between the 2nd level sub-structures in the 2nd level structure should satisfy
Successively,the distance Di between the ith level sub-structures in the ith level structure should satisfy
Both sides of the inequalities (14a)-(14c) are divided by d0 to get the normalized and unified formulation as
Through the summation formula for infinite geometric series,we get
By combing inequalities (12),(13),and (14e),we have
The above inferential process includes all gaps without omission,hereof,the inequality (15) is exactly the condition for the infinite growth of the N-segment line.
If the inequality (15a) is violated,connection or overlapping is inevitable,and multilevel structures can only grow to finite level. The inequality (15a) shows that the topological invariant N defines the upper bound for infinite growth.
Because (15a) is violated,the fractal snowflake in Fig. 10 can merely grow to finite levels. If the inequality (15b) is violated,even the first level structure cannot grow from the cell element. Therefore,inequality (15b) or (13) is called “the permissible condition for growth”. 5.6 Topological invariant and local connectivity
(8a) shows that the topological invariant N is the weighted factor of the self-similar ratio rs(2). In other words,the topological invariant N directly controls the translation movement. In other words,the topological invariant N regulates the topological evolution through control of translational movement.
From (8a),the following inferences may be deduced.
When  identically. Thereof,the connection occurs first
between the highest level sub-structures of the N-segment line. Noticeably,the highest level
sub-structures are always the finest structures at small scale. Hence,the micro connection may
occur first in the highest level sub-structures of the N-segment line.
identically. Thereof,the connection occurs first
between the highest level sub-structures of the N-segment line. Noticeably,the highest level
sub-structures are always the finest structures at small scale. Hence,the micro connection may
occur first in the highest level sub-structures of the N-segment line.
When  identically. Because the inequality (15a) is violated,
the connection or overlapping will occur between the 1st level sub-structures in the ith level
structure. Notably,the 1st level sub-structures are always the coarsest structures at large scale.
Thus,the macro connection must occur first in the 1st level sub-structures of the N-segment
line.
6 Topological invariant and conservation laws
identically. Because the inequality (15a) is violated,
the connection or overlapping will occur between the 1st level sub-structures in the ith level
structure. Notably,the 1st level sub-structures are always the coarsest structures at large scale.
Thus,the macro connection must occur first in the 1st level sub-structures of the N-segment
line.
6 Topological invariant and conservation laws
Reference [9] confirmed that the critical (mutation) point of topological evolution in fractal
snowflakes is (rs)cr =  . In this case,the fractal snowflake is called a “super” one. In terms of
the above proposition,rs(1) = rs(2) =
. In this case,the fractal snowflake is called a “super” one. In terms of
the above proposition,rs(1) = rs(2) =  is also the critical point of self-similar ternary-segment
line. Just as the super fractal snowflake,at the critical point,the self-similar ternary-segment
line is also of various conservation properties. A question may be asked: under the proportional
movement transformation groups,whether or not conservation laws of the N-segment line are
controlled by a specific self-similar ratio
is also the critical point of self-similar ternary-segment
line. Just as the super fractal snowflake,at the critical point,the self-similar ternary-segment
line is also of various conservation properties. A question may be asked: under the proportional
movement transformation groups,whether or not conservation laws of the N-segment line are
controlled by a specific self-similar ratio  ? The answer is positive.
6.1 Topological invariant and conservation of solid metric
? The answer is positive.
6.1 Topological invariant and conservation of solid metric
Suppose that the solid length of the initial segment is d0. In the N-segment line,the total solid length in the 1st level structure is Nd1. The total solid length in the 2nd level structure is N2d2. The total solid length in the ith level structure is Nidi. If the solid length is conservative, we have


When the solid metric is conservative,the self-similar ratio of the proportional compressive
movement will take the critical value determined by the topological invariant N. If N = 3,
rs(1) =  is the condition for the solid metric conservation of ternary-segment line (or fractal snowflakes).
is the condition for the solid metric conservation of ternary-segment line (or fractal snowflakes).
rs(1) =  marks the critical transition. If rs(1) <
marks the critical transition. If rs(1) <  ,the total length of solid segments
decreases gradually. If rs(1) >
,the total length of solid segments
decreases gradually. If rs(1) >  ,the total length of solid segments increases gradually. Because
rs(1) >
,the total length of solid segments increases gradually. Because
rs(1) >  violates the inequality (15a),the N-segment line can only grow to finite level.
violates the inequality (15a),the N-segment line can only grow to finite level.
When the solid metric of the N-segment line is conservative,(8a) degenerates to
6.2 Topological invariant and evolution of identical gaps
(8a) illustrates that the dimensionless gap  (i,j) is constrained by the structural level number
i and the sub-structural level number j. If
(i,j) is constrained by the structural level number
i and the sub-structural level number j. If  (i,j) is irrelevant to the sub-structural level number
j,then the width of all gaps in the ith level structure is identical. According to (8a),to make
(i,j) is irrelevant to the sub-structural level number
j,then the width of all gaps in the ith level structure is identical. According to (8a),to make
 (i,j) independent of the number j,the following condition must be satisfied:
(i,j) independent of the number j,the following condition must be satisfied:

When the distribution of gaps is homogeneous,the self-similar ratio of the proportional
translational movement must take the critical value determined by the topological invariant N.
If N = 3,rs(2) =  is the condition of the identical (or homogeneous) gaps of ternary-segment
line (or fractal snowflakes).
is the condition of the identical (or homogeneous) gaps of ternary-segment
line (or fractal snowflakes).
When the gaps of the N-segment line are homogeneous,(8a) degenerates to
The following inferences may be drawn:
(a) As long as rs(2)  ,gaps in the N-segment line will be distributed heterogeneously.
,gaps in the N-segment line will be distributed heterogeneously.
(b) If rd < rs(1) or rs(1) >rs(2) =  ,the N-segment line can only grow to finite level. At a
certain level,homogeneous gaps will vanish at the same time,and adjacent line segments will
connect or overlap simultaneously (see Fig. 22). For rs(1) ≠ rs(2),the N-segment line is not
self-similar.
,the N-segment line can only grow to finite level. At a
certain level,homogeneous gaps will vanish at the same time,and adjacent line segments will
connect or overlap simultaneously (see Fig. 22). For rs(1) ≠ rs(2),the N-segment line is not
self-similar.
 |
Fig. 22. Homogeneous finite growth of N-segment line (take 5th-segment line with rs(1) =  and
rs(2) = and
rs(2) =  as example) as example) |
(c) If rd > rs(1) and rs(1) < rs(2) =  ,the N-segment line can grow to infinite level. In
this case,all the homogeneous gaps will tend to vanish at the same time,while adjacent substructures
will tend to connect simultaneously (see Fig. 23). For rs(1) ≠ rs(2),the N-segment
line is not self-similar.
,the N-segment line can grow to infinite level. In
this case,all the homogeneous gaps will tend to vanish at the same time,while adjacent substructures
will tend to connect simultaneously (see Fig. 23). For rs(1) ≠ rs(2),the N-segment
line is not self-similar.
 |
Fig. 23. Homogeneous infinite growth of N-segment line (take 5th-segment line with rs(1) =  and
rs(2) = and
rs(2) =  as example) as example) |
Under similar proportional transformation groups,there is rs(1) = rs(2) = rs,and (8a) degenerates to
In this situation,the N-segment line is of strict self-similarity. Two cases are discussed as follows:
(a) If rs(1) = rs(2) = rs >  or rd < rs(1) = rs,for the inequality (15) is violated,the
self-similar N-segment line will connect or overlap at finite level.
or rd < rs(1) = rs,for the inequality (15) is violated,the
self-similar N-segment line will connect or overlap at finite level.
(b) If rs(1) = rs(2) = rs <  and rd ≥ rs(1) = rs,for the inequality (15) is obeyed,the
self-similar N-segment line can grow to infinite level,and a N-segment fractal is formed. At
this moment,for a fixed rs and varied rd,one family N-segment fractals may be obtained.
Different rs will lead to different (infinite) families of N-segment fractals. According to (18),
even in the same family,different members with different rd may have different distributions in
gaps.
7.2 Topological invariant and super family of N-segment fractal line
and rd ≥ rs(1) = rs,for the inequality (15) is obeyed,the
self-similar N-segment line can grow to infinite level,and a N-segment fractal is formed. At
this moment,for a fixed rs and varied rd,one family N-segment fractals may be obtained.
Different rs will lead to different (infinite) families of N-segment fractals. According to (18),
even in the same family,different members with different rd may have different distributions in
gaps.
7.2 Topological invariant and super family of N-segment fractal line
In the above infinite fractal families,there is a particular one corresponding to rs(1) = rs(2) =
rs =  . It is called the “super family”. In this case,(8a) degenerates to
. It is called the “super family”. In this case,(8a) degenerates to
The term “super family” is used because this family has super properties as follows.
The first super property is the conservation of the total solid length. Because rs(1) = rs = ,
for each member in this family,the total solid length of each level is conservative. This displays
the invariance of the total solid length of each level structure.
,
for each member in this family,the total solid length of each level is conservative. This displays
the invariance of the total solid length of each level structure.
The second one is the homogeneity in gaps at each level structure. For rs(2) = rs =  ,for
each member in this family,the gaps in each level structure are homogeneous.
,for
each member in this family,the gaps in each level structure are homogeneous.
The third one is the self-similarity of gaps between adjacent structures. From (19),we have
This ratio is irrelevant both to the sub-structural level number j and to the structural level number i. It means that the self-similarity exists in gaps between adjacent structures. Furthermore,the self-similar ratio also depends on the topological invariant N.
The fourth one is the connectivity at extreme state. By rs(1) = rs(2) = rs =  ,
, = 0
is derived from (19),i.e.,all members in this family are of a wonderful common property: when the structural level number tends to infinite,the structure tends to connect simultaneously both
locally and globally.
= 0
is derived from (19),i.e.,all members in this family are of a wonderful common property: when the structural level number tends to infinite,the structure tends to connect simultaneously both
locally and globally.
Now,the confusion in the introduction may be explained,i.e.,the fractal snowflakes in Fig. 7 and Fig. 9 are not the same piece because rd is different. However,even though they are different,both of them are members of the super family,and may tend to connection simultaneously at the extreme state.
In addition,(19) shows that there are infinite rd which satisfies rd ≥  ,i.e.,there are
infinite members in the super family of the N-segment fractals. In fact,any regular fractal set
(e.g.,the Cantor set) is not unique but a large family including infinite members. Up to now,
we can make a proposition,i.e.,because N may be taken as any natural number with N ≥ 2,
as far as the N-segment fractal is concerned,the super family is not an isolated case,but a
general and objective existence in fractal geometry.
7.3 Most homogeneous N-segment fractal line in super family
,i.e.,there are
infinite members in the super family of the N-segment fractals. In fact,any regular fractal set
(e.g.,the Cantor set) is not unique but a large family including infinite members. Up to now,
we can make a proposition,i.e.,because N may be taken as any natural number with N ≥ 2,
as far as the N-segment fractal is concerned,the super family is not an isolated case,but a
general and objective existence in fractal geometry.
7.3 Most homogeneous N-segment fractal line in super family
In the super family,there is a special member who satisfies

In this case,(19) degenerates to
Then,the practical width of gaps is

According to the definition of the proportional movement transformation groups,the solid length of each segment in the ith level structure is

The following formulation is deduced immediately:

Thereof,the unique properties of this member are as follows: in the ith level structure,all the solid segments are identical,and all the gaps are identical. Furthermore,the widths of the segment and the gap are also identical (see Fig. 24). Hereby,this is the most homogeneous N-segment fractal.
 |
| Fig. 24. Most homogeneous N-segment fractal line |
From (19),in the super family of the N-segment line,there is the most special member who satisfies

Then,(19) degenerates to
The N-segment fractal line is completely continuous with

The gaps between segments identically equal to zero,which are continuous segments (see Fig. 25). In other words,infinite segments with identical length form a fractal sequence. The following proposition may be made.
Proposition 4 The continuous space is the most special case of fractal space.
Noticeably,(22) does not include explicitly the topological invariant N. In other words, the above proposition is valid for any N-segment fractal,and the continuity of the continuous segment sequence is independent of the topological invariant N.
 |
| Fig. 25. Continuous N-segment fractal line (take 5th-segment line as example) |
The above proposition is closely related to our daily life. It explains accurately the meanings of scale systems in rulers. In a continuous ruler (see Fig. 26),either the ternary scale system or the decimal scale system can be selected. The relation between scale systems in rulers and fractals has been discussed in details in Ref. [12],and will not be repeated here. It is sure that the ternary scale system corresponds to the ternary-segment fractal,and the decimal scale system corresponds to the decimal-segment fractal[12]. However,no matter what system is adopted,and no matter how to mark the scale,the continuity of the ruler will not change.
 |
| Fig. 26. Rulers of binary system and decimal system |
Although fractal snowflake is just an example,the concepts and ideas refined from which are of inspiration and universality. The concept of proportional movement is the core of this paper. It is deduced from snowflake-like fractal patterns. But as an abstracted concept,it is universally applicable. Based on this concept,the proportionalmovement mode is abstracted. The (similar) proportional movement transformation group is defined. The topological invariant properties of N-segment line are exposed. Obviously,without fractal snowflakes,we cannot abstract the concepts of proportional movement and reveal the invariant properties of multilevel structures.
From fractal snowflake to N-segment (fractal) line,we can find that in many self-similar multilevel structures and fractal structures,the topological invariant plays decisive roles in growth kinematics. It is sure that all critical points in the growth process of fractal structures are controlled by the topological invariant. If (rs(1),rs(2),rd) is regarded as a parameter space, then the topological invariant will be the most important bifurcation point in this space.
| [1] | Baudry, J., Tajkhorshid, E., Molnar, F., Phillips, J., and Schulten, K. Molecular dynamics study of bacteriorhodopsin and the purple membrane. Journal of Physical Chemistry B, 105(5), 905-918 (2001) |
| [2] | Prozorov, T., Palo, P., Wang, L., Nilsen-Hamilton, M., Jones, D., Orr, D., Mallapragada, S. K., Narasimhan, B., Canfield, P. C., and Prozorov, R. Cobalt ferrite nanocrystals: out-performing magnetotactic bacteria. ACS NANO, 1, 228-233 (2007) |
| [3] | Du, J., Niu, H., Dong, J. Y., Dong, X., and Han, C. C. Self-similar growth of polyolefin alloy particles in a single granule multi-catalyst reactor. Advanced Materials, 20, 2914-2917 (2008) |
| [4] | Yin, Y., Zhang, T., Yang, F., and Qiu, X. M. Geometric conditions for fractal super carbon nanotubes with strict self-similarities. Chaos, Solitons and Fractals, 37, 1257-1266 (2008) |
| [5] | Yin, Y., Yang, F., Zhang, T., and Fan, Q. S. Growth condition and growth limit for fractal super fibers and fractal super tubes. International Journal of Nonlinear Sciences and Numerical Simulations, 9(1), 96-102 (2008) |
| [6] | Yin, Y., Yang, F., Fan, Q. S., and Zhang, T. Cell elements, growth modes and topology evolutions of fractal supper fibers. International Journal of Nonlinear Sciences and Numerical Simulation, 10(1), 1-12 (2009) |
| [7] | Yin, Y. J., Yang, F., Li, Y., and Fan, Q. S. Fractal geometry and topology abstracted from hair fibers. Applied Mathematics and Mechanics (English Edition), 30(8), 983-990 (2009) DOI 10.1007/s10483-009-0804-5 |
| [8] | Yin, Y., He, B., Yang, F., and Fan, Q. S. Centroid evolution theorem induced from fractal super fiber or fractal super snowflakes. International Journal of Nonlinear Sciences and Numerical Simulation, 10(6), 805-809 (2009) |
| [9] | Yin, Y., Yang, F., and Fan, Q. S. Growth kinematics of fractal super snowflakes. Chinese Science Bulletin, 55(7), 573-580 (2010) |
| [10] | Yin, Y. J., Li, Y., Yang, F., and Fan, Q. S. Multiple-cell elements and regular multifractals. Applied Mathematics and Mechanics (English Edition), 31(1), 55-65 (2010) DOI 10.1007/s10483- 010-0106-2 |
| [11] | Yin, Y. J., Yang, F., and Fan, Q. S. Isologous fractal super fibers or fractal super lattices. International Journal of Electrospun Nanofibers and Applications, 2(3), 193-201 (2008) |
| [12] | Peitgen, H. O., Jürgens, H., and Saupe, D. Chaos and Fractals: New Frontiers of Science (in Chinese), National Defense Industry Press, Beijing, 202-203 (2010) |
 2015, Vol. 36
2015, Vol. 36



































