Shanghai University
Article Information
- He LI, Dan LIU, Lai JIANG, Chunyu ZHAO, Bangchun WEN. 2015.
- Self-synchronization theory of dual motor driven vibration system with two-stage vibration isolation frame
- Appl. Math. Mech. -Engl. Ed., 36(2): 265-278
- http://dx.doi.org/10.1007/s10483-015-1905-7
Article History
- Received 2014-1-15;
- in final form 2014-5-30
The idea of self-synchronization vibration system comes from the phenomena of synchronization. Blekhman et al.[1] and Blekhman and Yaroshevich[2] proposed the self-synchronization theory of vibration system driven by two induction motors. When the structure parameters of the two motors meet the requirements,the system can be operated as synchronously. Blekhman et al.[3] also found that even if the revolving speed and the angular phase difference of the two eccentric rotors were disturbed or one of the motors was powered off,the system could still be operated as synchronously.
Sperling[4, 5] described a well suited method for the derivation of the conditions for the existence and the stability of synchronization motion applying harmonic influence coefficients. Ragulskis et al.[6, 7] analyzed the self-synchronization of nonlinear dynamic system. The small parameter methods were used to a number of problems by Nagaev[8],which lead to better understanding of the self-synchronization theory.
Some scientists investigated the self-synchronization of motors having a limited power supplies (non-ideal system). Kononenko[9] analyzed the model of non-ideal system based on the pure mechanical model of the motor and by considering the stationary characteristic of the energy source. However,this analysis considering mechanical interactions between the oscillating system and the energy source is limited by an assumed straight line. Balthazar et al.[10, 11] studied the self-synchronization of four motors having limited power supply and mounted on a flexible structural frame support,where the velocity and phase differences in the responses were also analyzed graphically.
Wen[12] established a branch of the vibration utilization engineering with the selfsynchronization theory in engineering,and numerous self-synchronous vibration machines were invented. The structure of the synchronous machines can be significantly simplified by applying the self-synchronization theory. This theory also makes the maintenance easier and more convenient,and increases the reliability of the machines. Zhao et al.[13, 14, 15] developed the self-synchronization of the dual-motor and four-motor driven vibration system by the modified average method. He further explained the coupled dynamic characters and dynamic symmetry of the vibration system,and several methods were used to analyze the self-synchronization motion and to verify the self-synchronization of two motors.
The vibration from the operation of machine can affect the normal work,break the structure and the components of the machine,lower the rate of productivity,and harm human’s health. Thus,it is essential to implement the vibration isolation for reducing the dynamic load transmitted to the foundation. This paper focuses on the conditions of self-synchronization and stability of a dual-motor driven vibration system with a two-stage isolation vibration frame. A sufficiently large oscillation amplitude of the material box can be ensured on the vibration system in order to screen materials,and a reduction of the dynamic load transmitted to the foundation can be also achieved on the vibration system.
The structure of this paper is as follows. Section 2 establishes the motion equations of the vibration system. The conditions of implementing self-synchronization and motion stability are deduced in Section 3. Section 4 carries out numerical simulations to verify the selfsynchronization motion,and Section 5 provides the experimental results. Finally,the conclusions are given in Section 6. 2 Motion differential equations of vibration system
The dynamic model of a vibration system with a two-stage vibration isolation frame is shown in Fig. 1,consisting of a material box m1,a supporting rigid body m2,a vibration isolation frame mr,and two eccentric rotors m01 and m02. m1 is connected with m2 with springs,and kx and ky are the stiffness coefficients of the springs in the x- and y-directions,respectively. m2 is connected with mr with springs kz in the z-axis direction,and is fixed along the x- and y-directions. mr is supported by the elastic foundation kzr. O1 and O2 are rotational centers of m01 and m02,respectively. m01 and m02 are driven by two induction motors,which are installed symmetrically about the horizontal plane (Oxy) of the centroid O of m1. The rotational plane is δ (resonance excitation angle) against Oxy. The rotational centers of two eccentric rotors and the material box’s center of mass are along the same vertical axis. The two motors rotate in the same direction from the top view.
 |
| Fig. 1. Dynamic model of vibration system with two-stage vibration isolation frame |
The motion differential equations of the vibration system can be established by the Lagrange equation as follows:
where M1 is the mass of the vibration system in the x- and y-directions,M1 = m1+m01+m02, M2 is the mass of the vibration system in the z-axis direction,M2 = m1 + m2 + m01 + m02, mr is the mass of isolation vibration frame,m0i are the masses of exciters i (i = 1,2),J0i are the moments of inertia of the motor rotors i (i = 1,2),kx,ky,kz,and kzr are the stiffness coefficients of the springs in the x-,y-,z-,and zr-directions,respectively,fx,fy,fz,and fzr are the damping coefficients in the x-,y-,z-,and zr-directions,respectively,fd1 and fd2 are the damping coefficients of the two motors,φi are the phases of exciters i (i = 1,2),δ is the resonance excitation angle,r is the eccentric radius of each exciter,and Tei are the electromagnetic torques of the induction motors i (i = 1,2).Making


It is assumed that the average phase of the two eccentric rotors is ψ during steady operation, and the phase difference between the two eccentric rotors is 2α. It is given by
Thus,each phase of the two eccentric rotors is Meanwhile,the angular velocity of eccentric rotors is assumed as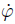 = ωm(t). Since the motion
of vibration system changes periodically,i.e.,the load of each motor changes periodically,the
average angular velocity ωm0 of the two eccentric rotors is constant in period. The instantaneous
variation coefficients of
= ωm(t). Since the motion
of vibration system changes periodically,i.e.,the load of each motor changes periodically,the
average angular velocity ωm0 of the two eccentric rotors is constant in period. The instantaneous
variation coefficients of 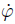 and
and 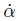 are assumed to be ε1 and ε2,respectively,which are the
functions of time t.
are assumed to be ε1 and ε2,respectively,which are the
functions of time t. 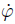 and
and 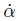 are given by
are given by
Substituting (5) into (4),and making v1= ε1 +ε2 and v2= ε1 −ε2,we can get the angular velocity and angular acceleration of two eccentric rotors as follows:
If two motors are operated with the same angular velocity,the average values of ε1 and ε2 over a single period must be zero,i.e.,ε1 = 0 and ε2 = 0.
Substituting (4) and (6) into (2) and introducing the following dimensionless parameters:

we can get the vibration responses of the system in the xr-direction as follows:
Differentiate (7) with respect to time t to obtain  ,and substitute them into
the last two equations of (1). Then,by integrating them over ψ = 0-2π and neglecting the high
order terms of v1 and v2,we get the average balanced equations of the two eccentric rotors as
follows:
,and substitute them into
the last two equations of (1). Then,by integrating them over ψ = 0-2π and neglecting the high
order terms of v1 and v2,we get the average balanced equations of the two eccentric rotors as
follows:

Compared with the change of ψ ( 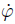 = ωm0) with respect to time t,those of α,v1,v2,
= ωm0) with respect to time t,those of α,v1,v2, 1,
and
1,
and  2 are very small. Therefore,these above five parameters are slow-changing parameters.
During the aforementioned integration over ψ = 0-2π,they can be assumed to be the middle
values of their integration,i.e.,α,v1,v2,
2 are very small. Therefore,these above five parameters are slow-changing parameters.
During the aforementioned integration over ψ = 0-2π,they can be assumed to be the middle
values of their integration,i.e.,α,v1,v2, 1,and
1,and  2,respectively.
2,respectively.
If the angular velocity of the two motors is near ωm0,their electromagnetic torques Te1 and Te2 can be expressed as
where Te01 and Te02 are the electromagnetic torques of the two motors when they are running in ωm0,i.e.,they are in steady operation,and ke01 and ke02 are the coefficients of stiffness of the two motors when they are running in ωm0.In (8),since the inertia coefficients of the shafts of the two motors,J01 and J02,are far less than m01r2 and m02r2,they can be neglected. Substituting (10) into (8) yields
Substituting (9) into (11),introducing the following dimensionless parameters:

and rearranging (11),we obtain the dimensionless coupled equation of the two eccentric rotors which describes the coupled relation between the two eccentric rotors as follows:
where

. If self-synchronization motion is realized on the system,ε1 = 0,and ε2 = 0. Substituting ε1 = 0 and ε2 = 0 into (12),we have u1 = 0 and u2 = 0. Rearranging (12),we get
where Tu is the kinetic energy of the eccentric rotor m01,and Tu = m01r2ωm02/2. TR1 and TR2 are the residual electromagnetic torques of motors 1 and 2,respectively,TR1 = Te01−fd1ωm0− TuWs0,and TR2 = Te02 − fd2ωm0 − Tuη2Ws0.Subtracting two parts of (13),
where TS is the torque of frequency capture,TS = m01r2ωM02|Wcc|,ΔTR is the difference between the residual electromagnetic torques of two motors,i.e.,

Since |sin 2α| ≤ 1,the condition of achieving self-synchronization of the two eccentric rotors
i.e.,the torque of frequency capture is equal to or greater than the difference between the residual electromagnetic torques of the two motors. 3.3 Stability condition of self-synchronization motion
When the parameters of this system meet the condition of achieving the synchronization,
the numerical solution of ωm0 and α can be solved by (13),which are expressed as ω*m0 and
α0[14],respectively. When the vibration system operates synchronously,(12) is linearized at
α = α0. Using the notation z = {ε1 ε2 Δα}T and considering  in (13),we get[15]
in (13),we get[15]

A reduction of the dynamic load transmitted to the foundation should be ensured on the vibration system in order to achieve vibration isolation. Therefore,the ratio of the mass mr of the isolation vibration frame to the mass M2 of the vibration system in the z-direction should be considered first during the parameters selection.
The parameters are selected as follows:

According to (7),it is known that the system amplitude in the z-direction is closely related to the value of μz. The greater value of μz tends to result in a greater value of the system amplitude in the z-direction. The amplitude ratio of isolation vibration frame to the system in the z-direction is τμzr/μz. With a smaller value of τμzr/μz,the vibration isolation ability will get stronger. When τ = 2,μz and τμzr/μz are closely related to the frequency ratio in the zand zr-directions. The relation curves are shown in Fig. 2.
 |
| Fig. 2. Relation between μz,τμzr/μz and parameters nz,nzr of vibration system |
As seen in Fig. 2(a),it is only when nzr is small enough,the whole system is possible to achieve resonance in the z-direction. When the resonance happens,the material box suffers a big amplitude. Each value of nzr corresponds to a value of nz,and it is obvious that when nzr = 0.3,nz = 0.9,the smaller value of nzr is,the bigger value of nz is. But the resonance amplitude slightly decreases.
From Fig. 2(b),when nzr ≥ 1,it can be seen that the amplitude of isolation vibration frame is larger than the amplitude in the z-direction of the whole system. Therefore,the vibration isolation frame has no effect on the system. When nzr < 1,the value of nzr will become smaller,which means that the vibration isolation frame has better effect on the vibration system. When the value of nzr is designated,with the increasing value of nz,τμzr/μz decreases continuously and the vibration isolation effect gets better.
It can be seen in Fig. 2 that on the basis of a relatively small value of nzr,a proper value of nz is selected in order to make resonance in the z-direction realized on the system. This proper value of nz can make the amplitude of the system in the z-direction big enough so as to meet the need of screening the materials. At the same time,this relatively small value of nzr can make the system achieve vibration isolation in the zz-direction. To sum up,the parameters should be selected as follows:

The mass parameters of the vibration system are designated as follows:


 |
| Fig. 3. Results of numerical simulation for self-synchronization motion of vibration system: (a) rotational velocities of two motors; (b) phase difference between two eccentric rotors; (c) displacement in x-direction; (d) displacement in y-direction; (e) displacement in z-direction; (f) displacement in zr-direction |
As shown in Fig. 3,when t = 4 s,the revolving speed of two motors reaches the same value (about 993.1 r/min),and the phase difference between the two eccentric rotors stabilizes at about 181.4◦. The displacement in every direction tends to be stable. At the moment,the π- phase self-synchronization and linear motion in the z-direction can be realized on the vibration system. Furthermore,the oscillation amplitude of the material box in the z-direction remains stable at about 1.19mm,and the oscillation amplitude of the isolation frame in the zr-direction is about 0.04mm. Therefore,a good vibration isolation effect is achieved on the system.
When t = 6 s,the power supply of motor 2 is cut off. During this process,the revolving speed of two motors decreases to about 992.1 r/min and the phase difference increases to about 181.9◦. But the system’s vibration in every direction is still stable. The self-synchronization motion of two motors continues. When t = 9s,a 10◦ phase disturbance is added to the motor 2. The phase difference turns to 191.9◦. Meanwhile,the revolving speed of two motors and the system vibration in every direction start to fluctuate. After about 1.5 s,the system vibration returns to the steady state. So the system can automatically adjust the phase difference and recovers the steady state. To sum up,the π-phase self-synchronization,vibratory synchronization transmission,and stability of self-synchronization operation of the vibration system can be realized. It can also meet the needs to screen the materials and reduce dynamic load to the foundation. 5 Experimental verification
The testing and analyzing system of the self-synchronous vibration system is shown in Fig. 4. The displacement is obtained by the accelerometer,and the revolving speed and the phase difference are obtained by the Laser Tacho Probe. The B&K data acquisition hardware is used to analyze the sensor signal. The experimental results are described in Table 1 and Fig. 5. As shown in Table 1 and Fig. 5,speed synchronization is realized on the two motors when the synchronous speed is 989 r/min. The phase difference between two eccentric rotors stands at 170 degree,which means that π-phase self-synchronization is nearly achieved on the system. Stable periodic motions are achieved on the vibration system in all directions,i.e., the x-,y-,and z-,and zr-directions. The vibration amplitudes in x- and y-directions stabilize at 0.099 6mm and 0.092 1mm,respectively,and they are small enough to be neglected. The vibration amplitudes in the z- and zr-directions remain stable at 1.52mm and 0.465mm,respectively, which demonstrates that the effect of the isolation vibration is significant. Then, the power supply of motor 2 is cut off. As shown in the Figs. 5(g) and 5(h),the phase difference between two eccentric rotors stands at 169 degree,which is sight away from π-phase self-synchronization. Even if the power of one of the motors is cut off,the speed synchronization at 988 r/min can be also achieved on the two motors.
 |
| Fig. 4. Testing and analyzing system of synchronous vibration system |
 |
| Fig. 5. Experimental curves of parameters of vibration system: (a) synchronous revolving speed of two motors; (b) phase difference between two eccentric rotors; (c) displacement in x-direction; (d) displacement in y-direction; (e) displacement in z-direction; (f) displacement in zr-direction; (g) synchronous revolving speed of two motors after cutting off motor 2; (h) phase difference between two eccentric rotors after cutting off motor 2 |
As seen from the comparison between the experimental results and numerical simulation results,the parameter values are generally the same. The simulation results are accurate and reliable. 6 Conclusions
In this paper,the conditions of self-synchronization and motion stability of a dual-motor driven vibration system with a two-stage vibration isolation frame are studied. By the Lagrange equations,the differential equations of the vibration system are obtained,and the dimensionless coupled equation of the eccentric rotors is obtained by a modified average small parameter method. Then,the conditions of achieving self-synchronization and motion stability are deduced. At last,the numerical simulations and experiments are carried out to verify the results of the theoretical analysis. The conclusions are summarized as follows:
(i) If TS ≥ |ΔTR| is satisfied,i.e.,the torque of frequency capture is equal to or greater than the difference between the residual electromagnetic torques of two motors,and selfsynchronization motion can be achieved on the vibration system.
(ii) According to the Routh-Hurwitz criterion,it is found that the condition of selfsynchronization motion stability is H1 > 0,H3 > 0,4H1H2 − H0H3 > 0.
(iii) The system amplitude in the z-direction is closely related to the value of μz. The greater value of μz is,the greater value of the system amplitude in the z-direction is. And the amplitude ratio of isolation vibration frame to the system in the z-direction is τμzr /μz . With a smaller value of τμzr /μz ,the vibration isolation ability will get stronger. μz and τμzr /μz are closely related to the frequency ratio in the z-direction nz ,the zr -direction nzr ,and the isolation mass ratio τ. For obtaining the better isolation effect,τ = 2,nzr = 0.3,and nz = 0.9 are chosen. Under the condition,the vibration system can meet the needs of screening the materials and get strong vibration isolation ability to reduce the dynamic load to the foundation. (iv) The numerical simulations prove that when the vibration system meet the conditions of self-synchronization and motion stability,the stable π-phase self-synchronization,vibratory synchronization transmission,and strong vibration isolation ability can be achieved on the vibration system.
(v) The self-synchronization experiments of the vibration system are conducted. As seen from the comparison between the experimental results and numerical simulation results,the parameter values are basically the same. The simulation results are accurate and reliable.
| [1] | Blekhman, I. I., Fradkov, A. L., Nijmeijer, H., and Pogromsky, A. Y. On self-synchronization and controlled synchronization. System & Control Letters, 31(5), 299-305 (1997) |
| [2] | Blekhman, I. I. and Yaroshevich, N. P. Extension of the domain of applicability of the integral stability criterion (extremum property) in synchronization problems. Journal of Applied Mathematics and Mechanics, 68(6), 839-864 (2004) |
| [3] | Blekhman, I. I., Fradkov, A. L., Tomchina, O. P., and Bogdanov, D. E. Self-synchronization and controlled synchronization: general definition and example design. Mathematics and Computers in Simulation, 58(4), 367-384 (2002) |
| [4] | Sperling, L. Selbstsynchronisation statisch und dynamisch unwuchtiger vibratoren (in German). Technische Mechanik, 14(1), 61-76 (1994) |
| [5] | Sperling, L. Selbstsynchronisation statisch und dynamisch unwuchtiger vibratoren, teil II ausführung und beispiele (in German). Technische Mechanik, 14(2), 85-96 (1994) |
| [6] | Ragulskis, K. M. Mechanisms on the Vibrating Base (in Russian), Lithuanian Academy of Sciences, Kaunas, 56-69 (1963) |
| [7] | Ragulskis, K. M., Vitkus, I. I., and Ragulskiene, V. L. Self-Synchronization of Systems (in Russian), Mintis, Vilnius, 156-184 (1965) |
| [8] | Nagaev, R. F. Dynamics of Synchronizing Systems, Spriger, Berlin, 255-287 (2003) |
| [9] | Kononenko, V. O. Vibrating System with Limited Power Supply, Illiffe, London, 11-19 (1969) |
| [10] | Balthazar, J. M., Felix, J. L. P., and Reyolando, M. L. R. Short comments on self-synchronization of two non-ideal sources supported by a flexible portal frame structure. Journal of Vibration and Control, 10(12), 1739-1748 (2004) |
| [11] | Balthaza, J. M., Felix, J. L. P., and Brasil, R. M. Some comments on the numerical simulation of self-synchronization of four non-ideal exciters. Applied Mathematics and Computation, 164(2), 615-625 (2005) |
| [12] | Wen, B. C. Recent development of vibration utilization engineering. Frontiers of Mechanical Engineering in China, 3(1), 1-9 (2008) |
| [13] | Zhao, C. Y., Zhu, H. T., Wang, R. Z., and Wen, B. C. Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linear motion, part I: theoretical analysis. Shock and Vibration, 16(5), 505-516 (2009) |
| [14] | Zhao, C. Y., Zhu, H. T., Bai, T. J., and Wen, B. C. Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linear motion, part II: numeric analysis. Shock and Vibration, 16(5), 517-528 (2009) |
| [15] | Zhao, C. Y., Zhu, H. T., Zhang, Y. M., and Wen, B. C. Synchronization of two coupled exciters in a vibrating system of spatial motion. Acta Mechanica Sinica, 26(3), 477-493 (2010) |
 2015, Vol. 36
2015, Vol. 36
























