Shanghai University
Article Information
- M. HAJIRAHIMI, F. MOKHTARI, A. H. FATOLLAHI. 2015.
- Exact identities for sessile drops
- Appl. Math. Mech. -Engl. Ed., 36(3): 293-302
- http://dx.doi.org/10.1007/s10483-015-1916-6
Article History
- Received 2014-04-25;
- in final form 2014-09-04
2. Department of Physics, Alzahra University, Tehran 91167, Iran
The studies of the profiles of the drops with the gravity effect in balance with the surface effects went back to more than a century ago[1] . The early solutions obtained by numerical methods went back to 1883[2] ,followed by the renewal updates extending and refining the original treatment[3,4,5,6] . Perturbative methods were used to give a large class of solutions for small drops in different situations[7,8,9,10,11,12] . If large drops can be theoretically assumed as an infinitely thin and large liquid film accompanied by the proper boundary conditions at the outer edge, the related problems can be solved by the singular perturbation techniques[13] . Ryley and Khoshaim[14] approximated the profile as a truncated oblate spheroid,and obtained the handy approximate analytical equations for the shape of the drop. Robertson and Lehman[15] gave a new numerical approach based on a different variational method. O’Brien[16] successfully used the method proposed in Ref. [15] to solve the problem on the shape of small sessile drops. Bashforth and Adams[2] used the singular perturbation technique to obtain the asymptotic expressions describing the shape of small sessile and pendant drops. Since the detailed information about the drops in different situations is particularly important for practical purposes, over the years,the optimization of matching methods between the experimental data and the calculated profiles has been the subject of many research pieces[17,18,19,20] . In fact,one of the most common methods to measure the liquid surface tension is based on the matching between the profiles of the calculated drops and the shapes of the measured drops. More recent efforts include presenting the approximate analytical solutions,developing more efficient methods for the numerical solutions[18,19,20,21,22,23] ,and giving the analytical solutions for the pendant liquids on flat and curved substrates[24] and the drops on the substrates with non-flat micro-structures[25] .
Heuristically,the balance between the surface effects and the bulk effects will fix the profile of a drop,the gravity will lower the center of the mass,and the surface energy will affect the drop areas and the contact region. For a drop with the density d,the volume V,and the surface tension γ ,the so-called bond number defined by the dimensionless combination V2/3dg/γ ,where g is the gravity constant,will determine whether weight has the dominant contribution or not. Mathematically,the Young-Laplace equation has to be satisfied at every point of the surface, i.e.,
where R1 and R2 are two principal radii of the curvature at the point,and ∆p ≡ p1 − pv is the pressure jump across the liquid-vapor interface. According to the hydrostatic laws,∆p and the surface equation are related. Therefore,the Young-Laplace equation can be turned to the differential equation. Then,with the appropriate boundary conditions,the profile of the drop can be determined. As one of the boundary conditions,the Young relation fixes the contact angle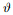 as follows:
where the adhesion coefficient is defined by the surface tension γ,the solid-liquid interfacial
energy γsv,and the solid-vapor interfacial energy γsl as follows[1]
:
as follows:
where the adhesion coefficient is defined by the surface tension γ,the solid-liquid interfacial
energy γsv,and the solid-vapor interfacial energy γsl as follows[1]
:
σ ≡ γsv + γ − γsl.
The purpose of this short note is to present a set of mathematical identities for sessile drops. By direct integration of the Young-Laplace relation over the entire surface of the drops,the exact identities can be derived for the sessile drops on flat and curved substrates. The geometrical parameters of the drops,including the contact radius,the curvature,and the height at the apex,are related by the identities. The importance of the mentioned parameters is that they are initially unknown,and are determined only after the complete solution is available. The validity of the identities is checked by various numerical solutions for both flat and curved substrates. 2 Numerical method
To provide the explicit check of the identities,several numerical solutions for the drops on
the flat and curved substrates are tabulated. In fact,there are a large number of numerical
methods to approach the solution of the Young-Laplace equation[20,21,22,23]
. Here,we present an
adapted version,which is the same as that shown in Ref. [21] by MATHEMATICA-7. The
starting point is to develop a set of first-order differential equations,by which the main YoungLaplace equation and the constraint on the volume are presented[21]
. For a drop with the
volume V,the density µ,the surface tension γ ,and the contact angle 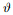 ,from a substrate given
by s(y),by the setup given in Fig. 1,we have[21]
,from a substrate given
by s(y),by the setup given in Fig. 1,we have[21]
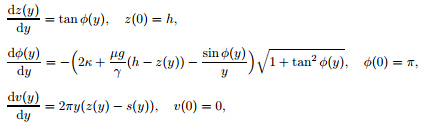
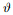 < 90° ,the following equations have to be satisfied[21]:
< 90° ,the following equations have to be satisfied[21]:
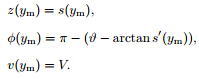
 |
| Fig. 1 Setup of numerical method |
Using the cylindrical coordinate setup given in Fig. 2,we can obtain the mean curvature of the axisymmetric surface z = ƒ(ρ) as follows:
where ƒ′ = dƒ/dρ. Moreover,the pressure jump gets contribution from the weight of the drop, leading to where d represents the density of the drop,g is the gravity constant,h is the height of the drop, and ∆pγ is the pressure jump originated from the surface tension[1] .The Young-Laplace equation is
where ƒ+ and f− are the upper and lower parts of the drop,respectively (see Fig. 2(b)),and κ := ∆pγ/(2γ ). The contact angle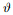 fixes the slope at the contact point. At the apex (h =
ƒ+(0)),we have R1 = R2. From (1),we can obtain that κ is the curvature at the apex.
fixes the slope at the contact point. At the apex (h =
ƒ+(0)),we have R1 = R2. From (1),we can obtain that κ is the curvature at the apex.The main issue with (5) is that h and κ are not known at the first place,and will be determined only after the complete solution is available. Therefore,at the starting point,the main equation is not fully known. Moreover,the contact radius ρ0 (see Fig. 2),as the limiting value for the variable ρ,is not known at the first place. Hereafter,the cases for flat and curved substrates are considered separately. 3.1 Flat substrate
The boundary conditions for 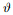 > 90° are
> 90° are
In the case,when 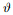 < 90° ,(7) and (8) are valid for ƒ+,ƒ-′ > 0,and ƒ′+ < 0.
In what follows,we mainly consider the case when
< 90° ,(7) and (8) are valid for ƒ+,ƒ-′ > 0,and ƒ′+ < 0.
In what follows,we mainly consider the case when 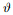 > 90° . The generalization to the case
when
> 90° . The generalization to the case
when 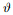 < 90° is rather straightforward. Integrating the Young-Laplace relation for the upper and lower parts of the drops,respectively,leads to
< 90° is rather straightforward. Integrating the Young-Laplace relation for the upper and lower parts of the drops,respectively,leads to
It is useful to check the above identities for the extreme cases,i.e.,without gravity and when the weight is the dominant force. In the case with zero gravity,only the surface effects are presented,and the shape is spherical. By direct insertion,it can be seen that the following equation satisfies the Young-Laplace relation (5):
which represents a sphere with the radius R whose center locates at z = z0. Using a geometrical argument (see Fig. 2),one can find Since on the surface of a sphere,the curvature is constant,we have k = 1/R. |
| Fig. 2 Geometry for setup described in text |
In the opposite extreme limit,when the weight has the dominant contribution,the surface
of the drops is flat (k → 0),and it forms a very large disc (ρ0: large). Keeping the terms
involved by dg/γ on both sides of (12),we find  3.2 Curved substrate
3.2 Curved substrate
Along the lines similar to the flat case,we can derive the identities for the curved substrate
as well. The main differences appear in the boundary condition and in the way that the volume
of the drop comes into the play. Here,the angle between the surfaces of the drop at the contact
point and the horizontal line,which is denoted by 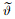 in Fig. 3,appears as a part of the boundary
conditions. For the cases with an obtuse angle,the boundary conditions read
in Fig. 3,appears as a part of the boundary
conditions. For the cases with an obtuse angle,the boundary conditions read
In the case when 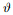 < 90° ,(17) is valid for ƒ+. In what follows,we mainly consider the
case when
< 90° ,(17) is valid for ƒ+. In what follows,we mainly consider the
case when 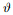 > 90° . The generalization to the case when
> 90° . The generalization to the case when 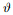 < 90° is rather straightforward.
Integrating the Young-Laplace relation for the upper and lower parts of the drops,respectively,
leads to
< 90° is rather straightforward.
Integrating the Young-Laplace relation for the upper and lower parts of the drops,respectively,
leads to
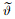 is the angle between the surfaces of the drop at the contact point and the horizontal line (see Fig. 3),for which we have
Subtracting (18) and (19) leads to
where
It can be shown that the identity (21) is valid for the case with the acute angle as well. It is
reminded that the identity (21) is an exact relation.
is the angle between the surfaces of the drop at the contact point and the horizontal line (see Fig. 3),for which we have
Subtracting (18) and (19) leads to
where
It can be shown that the identity (21) is valid for the case with the acute angle as well. It is
reminded that the identity (21) is an exact relation.
 |
Fig. 3 Four possible situations for drops on curved substrate s(ρ) and definition of angle 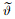 (single-arc) (single-arc) |
Now,we come to the case shown in Fig. 4,where ρ = 0 makes a dimple. For this case,the Young-Laplace relation reads
After integration,we have
By the relations for volumes,we have |
| Fig. 4 Drop with acute contact angle (double-arc) but concave surface |
To provide the direct tests of the identities obtained in the previous section,we present a
collection of numerical solutions by MATHEMATICA-7. The outputs of the numerical solutions
cover various parameters,including the contact radius ρ0,the apex height h,the curvature κ,and the angle 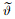 . Moreover,for each case,by taking four different values for the density of
the drop,the samples with different contributions of weight are presented. In all of the cases
presented below,the numerical values tabulated in Tables 2-3 satisfy the identities within the
significant digits of the reported values.
. Moreover,for each case,by taking four different values for the density of
the drop,the samples with different contributions of weight are presented. In all of the cases
presented below,the numerical values tabulated in Tables 2-3 satisfy the identities within the
significant digits of the reported values.
 |
 |
 |
In Fig. 5,the cases with drops on the flat substrate are presented. For these cases,the numerical values are given in Table 1. The plots of the numerical solutions with acute and obtuse contact angles on the curved substrates,which covers five situations,are presented in Figs. 6 and 7,respectively. The numerical values for these five situations are given in Tables 2 and 3.
 |
| Fig. 5 Plots of numerical solutions of Young-Laplace relation for drops on flat substrate with acute and obtuse contact angles with given values listed in Table 1 |
 |
| Fig. 6 Plots of numerical solutions of Young-Laplace relation for drops on curved substrate with numerical values given in Table 2 |
 |
| Fig. 7 Plots of numerical solutions of Young-Laplace relation for drops on curved substrate with numerical values given in Table 3 |
The study of drops at equilibrium is important for both theoretical and practical purposes. In particular,it is of great importance to study the relationship between the parameters related to the shape of the drop,including the contact radius,the height,and the apex curvature,and the parameters of the drop,such as the density and the surface tension. In the present short note,a set of mathematical identities,partly covering the above mentioned issues,are presented. In particular,for the cases of sessile drops on flat and curved substrates,by direct integration of the Young-Laplace relation over the entire surface of the drop,exact identities are derived. The geometrical parameters of the drop,including the contact radius and the curvature and height at the apex,are related by the identities. The importance of the mentioned parameters is that they are initially unknown and are determined only after the complete solution is available. The validity of the identities is checked by various numerical solutions for both flat and curved substrates. In particular,in each case,four situations with different weights (28 in total) are considered,and the values of the numerical solutions are presented,by which direct tests of the identities are possible.
Acknowledgement The authors are grateful to A. AGHAMOHAMMADI for his helpful discussion.| [1] | De Gennes, P. G. Wetting: statics and dynamics. Reviews of Modern Physics, 57, 827-863 (1985) |
| [2] | Bashforth, F. and Adams, J. C. An Attempt to Test the Theories of Capillary Attraction, Cam- bridge University Press, Cambridge (1883) |
| [3] | Staicopolus, D. N. The computation of surface tension and of contact angle by the sessile-drop method (I). Journal of Colloid and Interface Science, 17, 439-447 (1962) |
| [4] | Staicopolus, D. N. The computation of surface tension and of contact angle by the sessile-drop method (II). Journal of Colloid and Interface Science, 18, 793-794 (1963) |
| [5] | Padday, J. F. The profiles of axially symmetric menisci. Philosophical Transactions of the Royal Society A, 269, 265-293 (1971) |
| [6] | Hartland, S. and Hartley, R. W. Axisymmetric Fluid-Liquid Interfaces, Elsevier, Amsterdam (1976) |
| [7] | Chesters, A. K. An analytical solution for the profile and volume of a small drop or bubble symmetrical about the vertical axis. Journal of Fluid Mechanics, 81, 609-624 (1977) |
| [8] | Ehrlich, R. An alternative method for computing contact angle from the dimensions of a small sessile drop. Journal of Colloid and Interface Science, 28, 5-9 (1968) |
| [9] | Smith, R. W. and van de Ven, T. G. M. Profiles of slightly deformed axisymmetric drops. Journal of Colloid and Interface Science, 97, 1-8 (1984) |
| [10] | Shanahan, M. E. R. An approximate theory describing the profile of a sessile drop. Journal of the Chemical Society, Faraday Transactions 1: Physical Chemistry in Condensed Phases, 78, 2701- 2710 (1982) |
| [11] | Shanahan, M. E. R. Profile and contact angle of small sessile drops. Journal of the Chemical Society, Faraday Transactions 1: Physical Chemistry in Condensed Phases, 80, 37-45 (1984) |
| [12] | Fatollahi, A. H. On the shape of a lightweight drop on a horizontal plane. Physica Scripta, 85, 045401 (2012) |
| [13] | Rienstra, S. W. The shape of a sessile drop for small and large surface tension. Journal of Engineering Mathematics, 24, 193-202 (1990) |
| [14] | Ryley, D. J. and Khoshaim, B. H. A new method of determining the contact angle made by a sessile drop upon a horizontal surface (sessile drop contact angle). Journal of Colloid and Interface Science, 59, 243-251 (1977) |
| [15] | Robertson, W. M. and Lehman, G. W. The shape of a sessile drop. Journal of Applied Physics, 39, 1994-1996 (1968) |
| [16] | O'Brien, S. B. G. On the shape of small sessile and pendant drops by singular perturbation techniques. Journal of Fluid Mechanics, 233, 519-537 (1991) |
| [17] | Maze, C. and Burnet, C. A non-linear regression method for calculating surface tension and contact angle from the shape of a sessile drop. Surface Science, 13, 451-470 (1969) |
| [18] | Rotenberg, Y., Boruvka, L., and Neumann, A. W. Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces. Journal of Colloid and Interface Science, 93, 169-183 (1983) |
| [19] | Cheng, P., Li, D., Boruvka, L., Rotenberg, Y., and Neumann, A. W. Automation of axisymmetric drop shape analysis for measurements of interfacial tensions and contact angles. Colloids and Surfaces, 43, 151-167 (1990) |
| [20] | Kwok, D. Y. H. Contact Angles and Surface Energies, Ph.D. dissertation, University of Toronto, Toronto, 32 (1998) |
| [21] | Graham-Eagle, J. and Pennell, S. Contact angle calculations from the contact/maximum diameter of sessile drops. International Journal for Numerical Methods in Fluids, 32, 851-861 (2000) |
| [22] | Del Río, O. I. and Neumann, A. W. Axisymmetric drop shape analysis: computational methods for the measurement of interfacial properties from the shape and dimensions of pendant and sessile drops. Journal of Colloid and Interface Science, 196, 136-147 (1997) |
| [23] | Moy, E., Cheng, P., Policova, Z., Treppo, S., Kwok, D., Mack, D. R., Sherman, P. M., and Neumann, A. W. Measurement of contact angles from the maximum diameter of non-wetting drops by means of a modified axisymxnetric drop shape analysis. Colloids and Surfaces, 58, 215- 227 (1991) |
| [24] | Liu, J. L., Sun, J., and Liu, L. Elastica of a pendant droplet: analytical solution in two dimension. International Journal of Non-Linear Mechanics, 58, 184-190 (2014) |
| [25] | Liu, J. L., Feng, X. Q., and Yu, S. W. Morphology of liquid drops and thin films on a solid surface with sinusoidal microstructures. Acta Mechanica Sinica, 22, 315-322 (2006) |
 2015, Vol. 36
2015, Vol. 36





















