Shanghai University
Article Information
- F. MOAYYEDIAN, M. KADKHODAYAN. 2015.
- Modified Burzynski criterion with non-associated flow rule for anisotropic asymmetric metals in plane stress problems
- Appl. Math. Mech. -Engl. Ed., 36(3): 303-318
- http://dx.doi.org/10.1007/s10483-015-1913-6
Article History
- Received 2014-02-18;
- in final form 2014-08-18
The anisotropic character is always considered to accurately model the behavior of materials. In the current study,a brief review about this subject is firstly mentioned,and then a criterion for isotropic materials is extended for anisotropic pressure dependent metals with the non- associated flow rule (NAFR) in a new way.
Barlat et al.[1] proposed a general yield function to consider binary aluminum-magnesium sheet samples,which were fabricated by different processing paths. The yielding behavior was measured by the biaxial compression tests on the cubic specimens made from laminated sheet samples. Thamburaja and Anand[2] developed a crystal-mechanics-based constitutive model for polycrystalline shape-memory materials. The model was implemented in a finite element program and several experiments in the tension,compression,and shear performed on an initially textured polycrystalline Ti-Ni alloy. Thamburaja and Anand[3] showed the crystal- mechanics-based constitutive model for polycrystalline shape memory alloys[2],and predicted the super-elastic response of an initially-textured Ti-Ni alloy in (i) a proportional-loading and combined tension-torsion experiment and (ii) a path-change and tension-torsion experiment. Barlat et al.[4] proposed a new plane stress yield function to account for the anisotropy effects on the Cauchy stress tensor and the aluminum alloy sheets. Stoughton and Yoon[5] proposed an NAFR to fully account for the strength differential effect (SDE) based on a pressure sensitive yield criterion with isotropic hardening. Clausen et al.[6] presented an efficient return algorithm for the stress updating in the numerical plasticity computations for the yield criterion in the linear principal stress space composed of yield planes. Cvitanic et al.[7] developed a finite element formulation based on the non-associated plasticity. In the constitutive formulation, the isotropic hardening was assumed,and an evolution equation for the hardening parameter consistent with the principle of plastic work equivalence was introduced. Stoughton and Yoon[8] described a model,and explicitly integrated it into the yield criterion with no effect on the accuracy of the plastic strain components defined by the gradient of a separate plastic potential function based on an NAFR. Lee et al.[9] extended a hardening law based on a two-surface model to account for the general stress-strain effects of metal sheets,including the Bauschinger effect,the transient behavior,and the uncommon asymmetry. Aretz[10] presented the convexity of the yield function in the presence of a hydrostatic pressure sensitive yield stress. Hu and Wang[11] proposed a new theory,in which the yield function and the plastic potential were involved in the model. Taherizadeh et al.[12] developed an anisotropic material model based on the NAFR and the mixed isotropic-kinematic hardening,and implemented them into a user- defined material subroutine for the commercial finite element code ABAQUS. They defined both the yield function and the plastic potential in the form of Hill’s quadratic anisotropic function. The coefficients for the yield function were determined from the yield stresses in different material orientations,and those of the plastic potential were determined from the R-values in different directions. Mohr et al.[13] evaluated the accuracy of the quadratic plane stress plasticity models for a dual phase and an advanced high strength steel,and used the isotropic and anisotropic associated and non-associated quadratic plasticity models to describe the material behaviors. The results showed that the sheet materials exhibited a considerable direction- dependence on the R-ratio,and the uniaxial stress-strain curves had the same irrespective in the specimen direction. Huh et al.[14] evaluated the accuracy of common anisotropic yield functions,e.g.,Hill48,Yld89,Yld91,Yld96,Yld2000-2d,BBC2000,and Yld2000-18p based on the root-mean square error (RMSE) of the yield stresses,and obtained that the deduced Yld2000-18 yield function was the best to accurately describe the yield stresses and the R- values for sheet metals. Vadillo et al.[15] formulated an implicit integration of the elastic-plastic constitutive equations for the paraboloid case of Burzynski’s yield condition,and developed a tangent operator which was consistent with the integration algorithm. Taherizadeh et al.[16] developed a generalized finite element formulation of the stress integration method for the non-quadratic yield functions and potentials with mixed nonlinear hardening under the NAFR. Gao et al.[17] described a plasticity model for isotropic materials,which was a function of the hydrostatic stress and the second and third invariants of the stress deviator,and presented its finite element implementation. Coombs and Crouch[18] presented an analytical backward Euler stress integration for a volumetrically non-associated pressure sensitive yield function based on a modified Reuleaux triangle. The analytical solution was 2-4 times faster than a standard numerical backward Euler algorithm. Yu et al.[19] showed that the transformation started stress from austenitic phase to stress-induced martensitic phase increased with the increase in the ambient temperature. Based on the experimental observation,a single crystal constitutive model considering both transformation and plasticity was first established,and the interaction energy was introduced to consider the effect of the plasticity on the transformation. Then,an explicit scale-transition rule was adopted in the proposed micromechanical constitutive model. Park and Chung[20] developed a new formulation with the combined isotropic-kinematic hardening law. Yu et al.[21] constructed a new micromechanical constitutive model to describe the cyclic deformation of the polycrystalline Ni-Ti shape memory alloy presented under different thermo-mechanical cyclic loading conditions. Lou et al.[22] proposed an approach to extend the symmetric yield functions,considering the SDE in the sheet metals. The approach was successfully used to analyze the symmetric Yld2000-2d yield function,and the yield function was modified to describe the anisotropic yielding and the symmetric yielding of two aluminum alloys with small and strong SDEs. Safaei et al.[23] presented a non-associated plane stress anisotropic constitutive model with mixed isotropic-kinematic hardening. The quadratic Hill48 yield criterion and the non-quadratic Yld2000-2d yield criterion were considered in the NAFR model to account for the anisotropic behavior. Yu et al.[24] constructed a micromechanical constitutive model based on the crystal plasticity to describe the deformation behaviors of the polycrystalline Ni-Ti shape memory alloy under various thermo-mechanical loading conditions, and deduced the evolution equations of internal variables to power-law forms. Safaei et al.[25] described the anisotropy evolution in terms of both distortional hardening and variations of Lankford coefficients. An NAFR based Yld2000-2d anisotropic yield model was used,where the separate yield function and the plastic potential were considered.
In the current research,a pressure dependent isotropic criterion,i.e.,“Burzynski criterion”, for isotropic metals is newly extended to consider the anisotropy effects along with pressure dependency and the NAFR in a plane stress problem. It is shown that the new criterion is proper for anisotropic pressure asymmetric metals. 2 Modified Burzynski criterion as yield stress and plastic potential functions
To develop the Burzynski criterion to consider the anisotropic effects,a linear transformation is defined as follows:
where Lij (i,j = 1,2,3,6) are the components of a linear transformation matrix applied on the independent parameters σij (i,j = x,y) to obtain the modified deviatoric tensors sij (i,j = x,y). Lij (i,j = 1,2,3,6) can be defined in terms of αi (i = 1,2,· · · ,5) as follows: sij (i,j = x,y) can be expressed as follows: In the above equations,αi (i = 1,2,· · · ,5) are the parameters which can determine the anisotropy effects of the modified deviatoric stress tensors on the yield function. This idea arises from one of the linear transformations mentioned in the Yld2000-2d criterion[4]. In this case,the modified effective stress can be expressed as follows: To modify the hydrostatic stress,the following form is used: where σ6 and σ7 are two parameters related to the anisotropy effects in the yield function. Then,the modified Burzynski criterion for isotropic metals can be extended for anisotropic asymmetric metals as follows[15]: Generally,it can be stated that σ8 can consider the weight of the modified effective deviatoric stress,while σ9 and σ10 can consider the weight of the hydrostatic pressure in the modified Burzynski criterion. Inserting Eq. (3) into Eq. (4) and substituting the obtained result and Eq. (5) into Eq. (6) yield the modified Burzynski criterion in terms of the stress components as follows: All of these ten material parameters αi (i = 1,2,· · · ,10) can be determined by ten experimental data which will be given and explained in the next section. When αi = 1 (i = 1,2,· · · ,7),from Eqs. (3) and (5),we can see that the modified Burzynski criterion in Eq. (6) is equivalent to that of isotropic materials.To present the new corresponding pressure independent plastic potential function,the fol- lowing linear transformation is considered:
where and the the modified deviatoric stress tensors sij (i,j = x,y) can be determined by In the above equations,βi (i = 1,2,· · · ,5) are five independent parameters,which are related to the anisotropy effects in the plastic potential function. In this case,the modified effective stress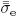 can be expressed by
can be expressed by
Now,by eliminating the effects of the pressure independency in the yield function,a new pressure independent plastic potential function is presented,i.e.,
Inserting Eq. (10) into Eq. (11) and substituting the obtained result into Eq. (12) yield the plastic potential function in terms of the stress components as follows:Moreover,the first differentiation of the proposed plastic potential function is useful for its calibration. Therefore,from Eq. (13),we have
3 Calibration of modified Burzynski criterion and its plastic potential function
The newly modified yield criterion can be calibrated by ten experimental data,i.e.,the
tensile yield stresses (σθT ) at 0°,45°,and 90°,the compressive yield stresses (σθC ) at 0°,15°,
30°,45°,75°,and 90° from the rolling direction,and the biaxial tensile yield stress (σbC ). The
related newly pressure,which is independent of the plastic potential function,can be calibrated
by six experimental data,i.e.,the tensile R-values ( ) at 0°,15°,45°,75°,and 90° from
the rolling direction,and the tensile biaxial R-value (
) at 0°,15°,45°,75°,and 90° from
the rolling direction,and the tensile biaxial R-value ( ). The effect of the pressure
dependency in this criterion can be automatically satisfied because of the inherent existence of
the modified hydrostatic stress in the yield function in Eq. (6). The proposed criterion has the
anisotropy effects and the pressure dependency effects[22].
3.1 Tensile,compressive,and biaxial yield stress tests
). The effect of the pressure
dependency in this criterion can be automatically satisfied because of the inherent existence of
the modified hydrostatic stress in the yield function in Eq. (6). The proposed criterion has the
anisotropy effects and the pressure dependency effects[22].
3.1 Tensile,compressive,and biaxial yield stress tests
For the tensile yield stress tests in the θ-direction from the rolling direction,it is considered that[22]
where θ is the angle from the rolling direction,and σθT is the tensile yield stress in the θ- direction. By inserting these values in Eq. (7),a second-order equation in terms of σθT can be obtained,i.e., Taking the positive root of this equation yields σθT as follows: where For the compressive yield stress tests in the θ-direction from the rolling direction,it is considered that With the same process as the previous one,the following second-order equation can be obtained: where For the balanced biaxial yield stress test,it is considered that Substituting these values into Eq. (7) yields a second-order equation in terms of σbC as follows: From the positive root,we have where 3.2 NAFR with tensile and biaxial R-value testsSince the plastic potential function is pressure independent,the NAFR for the plane stress problem is accepted. The NAFR takes the following form:
In this case,the thickness strain can be calculated by the incompressibility assumption as follows: The tensile R-value in the θ-direction from the rolling direction is denoted by RθT ,which can be obtained by The R-value in the balanced biaxial tension is defined by the ratio of the strain increment in the transverse direction to that in the rolling direction,and it can be obtained by 4 Parameter evaluation and RMSEs of yield stresses and R-values in yield and plastic functionsFrom Eqs. (17),(21),and (24),we can obtain αi (i = 1,2,· · · ,5) with the the yield function. From Eqs. (28) and (29),we can obtain βi (i = 1,2,· · · ,6) with the plastic potential function. In the current study,these sixteen material constants are calculated by the following sixteen experimental data:

These error functions are minimized by the downhill simplex method to identify the material parameters[14, 22]. The RMSEs of the tensile,biaxial,and compressive yield stresses with the tensile and biaxial R-values can be obtained by
The yield stresses and the R-values computed from experiments for the anisotropic materials Al 2008-T4 and Al 2090-T3 are presented in Tables 1-3[22].In this part,the yield surfaces are constructed by the modified Yld2000-2d criterion and the presented modified Burzynski criterion. The results are shown in Figs. 1-6 and compared with the experimental results for Al 2008-T4 (a BCC material) and Al 2090-T3 (an FCC material). The mechanical properties of these materials in different directions from the rolling direction are available in Tables 1-3. In Tables 4 and 5,the parameters αi (i = 1,2,· · · ,10) and βi (i = 1,2,· · · ,6) are computed for the yield and plastic potential functions expressed in Eqs. (7) and (13),respectively,by minimizing the error functions E1 and E2 in Eqs. (30) and (31) with the downhill simplex method.
 |
| Fig. 1 Yield and plastic potential surfaces for Al 2008-T4 |
 |
Fig. 2  -plane for Al 2008-T4for Al 2008-T4 -plane for Al 2008-T4for Al 2008-T4 |
 |
| Fig. 3 Yield and plastic potential surfaces for Al 2090-T3 |
 |
Fig. 4  -plane for Al 2090-T3 -plane for Al 2090-T3 |
 |
| Fig. 5 Comparison of yield stress directionality for Al 2008-T4 |
 |
| Fig. 6 Comparison of yield stress directionality for Al 2090-T3 |
The obtained yield and plastic potential surfaces for Al 2008-T4 are shown in Fig. 1. From the figure,we can see that the results of the modified Burzynski criterion are in the exterior of the results of the modified Yld2000-2d criterion in all quadrants. The difference between these criteria is more obvious in the third quadrant. However,both these two criteria can predict the experimental results properly. Therefore,it can be concluded that the presented modified Burzynski criterion can successfully predict the yield surface in the σxxσyy-plane for Al 2008-T4.
Figure 2 shows the modified effective stress 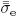 versus the modified hydrostatic pressure
versus the modified hydrostatic pressure  for Al 2008-T4 according to Eq. (6) and the parameters σ8,σ9,and σ10 in Table 4. It is
observed that a modified Burzynski Torre paraboloid is obtained.
for Al 2008-T4 according to Eq. (6) and the parameters σ8,σ9,and σ10 in Table 4. It is
observed that a modified Burzynski Torre paraboloid is obtained.
 |
 |
The obtained yield and plastic potential surfaces for Al 2090-T3 are shown in Fig. 3. From the figure,we can see that the results of the presented modified Burzynski criterion are in the exterior of those of the modified Yld2000-2d criterion in the first and third quadrants while are in the interior of those of the modified Yld2000-2d criterion in the second and fourth quadrants. However,both the two criteria can predict the experimental results properly. Therefore,it can be deduced that the presented modified Burzynski criterion is appropriate to predict the yield surface in the σxxσyy-plane for Al 2090-T3.
Figure 4 displays the modified effective stress 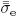 versus the modified hydrostatic pressure
versus the modified hydrostatic pressure
 for Al 2090-T3 according to Eq. (6) and the parameters σ8,σ9 and σ10 in Table 4. The
results show that a modified Burzynski ellipse is obtained and the effective deviatoric stress
and the hydrostatic pressure are independent.
for Al 2090-T3 according to Eq. (6) and the parameters σ8,σ9 and σ10 in Table 4. The
results show that a modified Burzynski ellipse is obtained and the effective deviatoric stress
and the hydrostatic pressure are independent.
As mentioned previously,the presented modified Burzynski Torre paraboloid and the mod- ified Burzynski ellipse are applicable to Al 2008-T4 and Al 2090-T3 for the prediction of the experimental results in the σxxσyy-plane.
Figure 5 shows the tensile and compressive yield stresses of Al 2008-T4 versus the angle from the rolling direction. From Fig. 5(a),we can see that the results of the presented modified Burzynski criterion underestimate in the range of 0° 6 θ 6 15° and overestimate the experi- mental data in the range of 15° 6 θ 6 90°. In general,the results of the modified Yld2000-2d criterion predict the tensile yield stresses more precisely in comparison with the experimental data. From Fig. 5(b),we can see that except θ = 30° and θ = 45°,the presented modified Burzynski criterion overestimates the experimental data. However,the obtained results are much more precise than those of the modified Yld2000-2d criterion.
Figure 6 illustrates the tensile and compressive yield stresses of Al 2009-T3 versus the angle from the rolling direction. From the figure,we can see that the tensile yield stresses obtained by the presented modified Burzynski criterion overestimate the experimental results at θ = 45° and θ = 60° while underestimate the experimental results at other θ. Moreover,the compressive yield stresses obtained by the presented modified Burzynski criterion underestimate the experimental results at θ = 15°,30°,75° while overestimate the experimental results at other θ.
From these observations,it can be concluded that the proposed modified Burzynski criterion is very suitable for predicting experimental results,especially for the compressive yield stresses of Al 2008-T4 and Al 2090-T3. In the current research,the number of the required data to calibrate the yield function for the compressive yield stresses increases from two (σ0C,σ90C) to seven (σ0C,σ15C,σ45C,σ60C,σ75C,σ90C). It is observed that the compressive yield stresses can predict the experimental results more ac- curately than the modified Yld2000-2d criterion. To calibrate the presented modified Burzynski criterion for the tensile yield stresses,we select three experimental data (σ0T,σ45T,σ90T),where σ0T is the same as that in the modified Yld2000-2d criterion. However,it is observed that the experimental results are nearer to the modified Yld2000-2d criterion. For the biaxial yield stress (σbC ),one point is selected for both the criteria,and the results are nearly the same (see Figs. 1 and 3). The relative errors for these cases are computed at the end of this section
In Fig. 7,the R-values for Al 2008-T4 are plotted versus various angles from the rolling direction. The results show that the presented modified Burzynski criterion underestimates the experimental results in the range of 0° 6 θ 6 45° while overestimates the experimental results in the range of 45° < θ 6 90°. In Fig. 8,for Al 2090-T3,the presented modified Burzynski criterion predicts all experimental results properly except at θ = 45°. Therefore,the presented modified Burzynski Torre paraboloid and ellipse are applicable for Al 2008-T4 and Al 2090-T3.
 |
| Fig. 7 Comparison of R-value directionality for Al 2008-T4 |
 |
| Fig. 8 Comparison of R-value directionality for Al 2090-T4 |
To obtain the presented plastic potential function,we select seven experimental data as follows: R0T,R15T,R45T,R60T,R75T,R90T. The number of the selected parameters is larger than that of the modified Yld2000-2d criterion,where three experimental data,i.e.,R0T ,R45T,R90T,are needed. The modified Yld2000-2d criterion can predict the experimental results more precisely for Al 2008-T4. However,for Al 2090-T3,the presented modified Burzynski criterion is much more accurate than the modified Yld2000-2d criterion,compared with the experimental results. To calibrate these criteria to predict RbT ,one point is selected for both the presented modified Burzynski criterion and the modified Yld2000-2d criterion. The obtained results show that both these criteria can be used to predict RbT .
Tables 6 and 7 show the relative errors for Al 2008-T4 and Al 2090-T3,respectively. The parameters EσT ,EσC ,EbT σ ,ERT,and ERbT are the relative errors for computing the tensile yield stress,the compressive yield stress,the tensile biaxial yield stress,the R-value,and the tensile biaxial R-value,respectively. For both materials,EσC obtained by the modified Burzynski criterion is less than that of the modified Yld2000-2d criterion. EbT σ and ERbT are close to zero. For Al 2090-T3,ERT obtained by the modified Burzynski criterion is less than that obtained by the modified Yld2000-2d criterion. needed. The modified Yld2000-2d criterion can predict the experimental results more precisely for Al 2008-T4. However,for Al 2090-T3,the presented modified Burzynski criterion is much more accurate than the modified Yld2000-2d criterion,compared with the experimental results. To calibrate these criteria to predict RbT ,one point is selected for both the presented modified Burzynski criterion and the modified Yld2000-2d criterion. The obtained results show that both these criteria can be used to predict RbT .
The Burzynski criterion for isotropic materials is extended for anisotropic asymmetric met-
als,considering the NAFR in plasticity. The presented modified yield function and the potential
function are pressure dependent and pressure independent. The presented yield function can
be calibrated with ten experimental data,i.e.,the tensile yield stresses (σθT ) at 0°,45°,and 90°,
the compressive yield stresses (σθC ) at 0°,15°,30°,45°,75°,and 90° from the rolling direction,
and the biaxial tensile yield stress (σbC ). The presented modified plastic potential function
can be calibrated by six experimental data,i.e.,the tensile R-values ( ) at 0°,15°,
45°,75°,and 90° from the rolling direction and the tensile biaxial R-value (
) at 0°,15°,
45°,75°,and 90° from the rolling direction and the tensile biaxial R-value ( ). The
downhill simplex method is used to solve ten and six high nonlinear equations for the yield and
plastic potential functions,respectively. The presented modified Burzynski criterion can also
be equipped for three-dimensional problems because of the pressure independency of its plastic
potential function. The modified Yld2000-2d criterion allows the associated flow rule and its
plastic potential to be pressure dependent. It is generally demonstrated that the presented
modified Burzynski criterion is more appropriate than the modified Yld2000-2d criterion in
predicting the experimental results.
). The
downhill simplex method is used to solve ten and six high nonlinear equations for the yield and
plastic potential functions,respectively. The presented modified Burzynski criterion can also
be equipped for three-dimensional problems because of the pressure independency of its plastic
potential function. The modified Yld2000-2d criterion allows the associated flow rule and its
plastic potential to be pressure dependent. It is generally demonstrated that the presented
modified Burzynski criterion is more appropriate than the modified Yld2000-2d criterion in
predicting the experimental results.
| [1] | Barlat, F., Maeda, Y., Chung, K., Yanagawa, M., Brem, J. C., Hayashida, Y., Lege, D. J., Matsui, K., Murtha, S. J., Hattori, S., Becker, R. C., and Makosey, S. Yield function development for aluminium alloy sheets. Journal of the Mechanics and Physics of Solids, 45, 1727-1763 (1997) |
| [2] | Thamburaja, P. and Anand, L. Polycrystalline shape-memory materials: effect of crystallographic texture. Journal of the Mechanics and Physics of Solids, 49, 709-737 (2001) |
| [3] | Thamburaja, P. and Anand, L. Superelastic behavior in tension-torsion of an initially-textured Ti-Ni shape-memory alloy. International Journal of Plasticity, 18, 1607-1617 (2002) |
| [4] | Barlat, F., Brem, J. C., Yoon, J. W., Chung, K., Dick, R. E., Lege, D. J., Pourboghrat, F., Choi, S. H., and Chu, E. Plane stress yield function for aluminum alloy sheets鈥攑art 1: theory. International Journal of Plasticity, 19, 1297-1319 (2003) |
| [5] | Stoughton, T. B. and Yoon, J. W. A pressure-sensitive yield criterion under a non-associated flow rule for sheet metal forming. International Journal of Plasticity, 20, 705-731 (2004) |
| [6] | Clausen, J., Damkilde, L., and Andersen, L. An efficient return algorithm for non-associated plasticity with linear yield criteria in principal stress space. Computers and Structures, 85, 1795- 1807 (2007) |
| [7] | Cvitanic, V., Vlak, F., and Lozina, Z. A finite element formulation based on non-associated plasticity for sheet metal forming. International Journal of Plasticity, 24, 646-687 (2008) |
| [8] | Stoughton, T. B. and Yoon, J. W. Anisotropic hardening and non-associated flow in proportional loading of sheet metals. International Journal of Plasticity, 25, 1777-1817 (2009) |
| [9] | Lee, M. G., Kim, S. J., Wagoner, R. H., Chung, K., and Kim, H. Y. Constitutive modeling for anisotropic/asymmetric hardening behavior of magnesium alloy sheets: application to sheet springback. International Journal of Plasticity, 25, 70-104 (2009) |
| [10] | Aretz, H. A consistent plasticity theory of incompressible and hydrostatic pressure sensitive met- als鈥擨I. Mechanics Research Communications, 36, 246-251 (2009) |
| [11] | Hu,W. andWang, Z. R. Construction of a constitutive model in calculations of pressure-dependent material. Computational Materials Science, 46, 893-901 (2009) |
| [12] | Taherizadeh, A., Green, D. E., Ghaei, A., and Yoon, J. W. A non-associated constitutive model with mixed iso-kinematic hardening for finite element simulation of sheet metal forming. International Journal of Plasticity, 26, 288-309 (2010) |
| [13] | Mohr, D., Dunand, M., and Kim, K. H. Evaluation of associated and non-associated quadratic plasticity models for advanced high strength steel sheets under multi-axial loading. International Journal of Plasticity, 26, 939-956 (2010) |
| [14] | Huh, H., Lou, Y., Bae, G., and Lee, C. Accuracy analysis of anisotropic yield functions based on the root-mean square error. AIP Conference Proceedings, 1252, 739-746 (2010) |
| [15] | Vadillo, G., Fernandez-Saez, J., and Pecherski, R. B. Some applications of Burzynski yield condi- tion in metal plasticity. Materials and Design, 32, 628-635 (2011) |
| [16] | Taherizadeh, A., Green, D. E., and Yoon, J. W. Evaluation of advanced anisotropic models with mixed hardening for general associated and non-associated flow metal plasticity. International Journal of Plasticity, 27, 1781-1802 (2011) |
| [17] | Gao, X., Zhang, T., Zhou, J., Graham, S. M., Hayden, M., and Roe, C. On stress-state dependent plasticity modeling: significance of the hydrostatic stress, the third invariant of stress deviator and the non-associated flow rule. International Journal of Plasticity, 27, 217-231 (2011) |
| [18] | Coombs, W. M. and Crouch, R. S. Non-associated Reuleaux plasticity: analytical stress inte- gration and consistent tangent for finite deformation mechanics. Computer Methods in Applied Mechanics and Engineering, 200, 1021-1037 (2011) |
| [19] | Yu, C., Kang, G. Z., Song, D., and Kan, Q. H. Micromechanical constitutive model considering plasticity for super-elastic NiTi shape memory alloy. Computational Materials Science, 56, 1-5 (2012) |
| [20] | Park, T. and Chung, K. Non-associated flow rule with symmetric stiffness modulus for isotropic- kinematic hardening and its application for earing in circular cup drawing. International Journal of Solids and Structures, 49, 3582-3593 (2012) |
| [21] | Yu, C., Kang, G. Z., Kan, Q. H., and Song, D. A micromechanical constitutive model based on crystal plasticity for thermo-mechanical cyclic deformation of NiTi shape memory alloys. International Journal of Plasticity, 44, 161-191 (2013) |
| [22] | Lou, Y., Huh, H., and Yoon, J. W. Consideration of strength differential effect in sheet metals with symmetric yield functions. International Journal of Mechanical Sciences, 66, 214-223 (2013) |
| [23] | Safaei, M., Zang, S. L., Lee, M. G., and Waele, W. D. Evaluation of anisotropic constitutive models: mixed anisotropic hardening and non-associated flow rule approach. International Journal of Mechanical Sciences, 73, 53-68 (2013) |
| [24] | Yu, C., Kang, G. Z., and Kan, Q. H. Crystal plasticity based constitutive model of NiTi shape memory alloy considering different mechanisms of inelastic deformation. International Journal of Plasticity, 54, 132-162 (2014) |
| [25] | Safaei, M., Lee, M. G., Zang, S. L., and Waele, W. D. An evolutionary anisotropic model for sheet metals based on non-associated flow rule approach. Computational Materials Science, 81, 15-29 (2014) |
 2015, Vol. 36
2015, Vol. 36









































