Shanghai University
Article Information
- Shuang LIU, Liqun CHEN. 2015.
- Outer synchronization of uncertain small-world networks via adaptive sliding mode control
- Appl. Math. Mech. -Engl. Ed., 36(3): 319-328
- http://dx.doi.org/10.1007/s10483-015-1911-6
Article History
- Received 2013-12-01;
- in final form 2014-07-16
2. Department of Mechanics, Shanghai University, Shanghai 200444, China;
3. Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Recently,great efforts have been devoted to the understanding of complex networks. Many systems in nature or society can be modeled as complex networks,e.g.,a set of objects connected with coupling[1]. Understanding such interwoven systems is a significant challenge. In 1960,Erdös and Rényi described a network with complex topology by a random graph. In 1998,focusing on the transition from a regular lattice to a random graph,Watts and Strogatz introduced an interesting model,i.e.,the small-world network[2]. To explore the possibility for the Watts-Strogatz model to be broken into unconnected cluster,Newman and Watts suggested a slight modification of the Watts-Strogatz model,i.e.,the Newman-Watts small-word network model[3]. These discoveries have led to dramatic advances in the field of complex network theory in the past years[4]. Researchers have paid their attention to many different aspects, e.g.,social network,food chain,neuronal network,electricity distribution network,and disease transmission network[5, 6, 7].
During the last decade,the dynamical properties of complex network have been widely characterized[8]. Synchronization,as one of these dynamical implications,has received a great deal of attention[9]. Many synchronization phenomena are examined[10],e.g.,complete synchronization, phase synchronization,generalized synchronization,and lag synchronization[11, 12, 13]. In the above literatures,for convenience,the synchronization inside a coupled network was treated as “inner synchronization” and the synchronization between two or more coupled complex networks was treated as “outer synchronization”[14]. Many approaches are used to study outer synchronization. Tang et al.[15] designed adaptive controllers to synchronize two coupled regular networks with identical or nonidentical topological structures. Wu et al.[16] used a nonlinear control scheme to study the outer synchronization between star coupled networks and ring networks. Li et al.[17] used a variable structure control strategy to investigate the global synchronization problem of two irregular couple networks. The above mentioned works are all about coupled networks with certain parameters. However,in practical situations,some or all of the network parameters may be unknown,and the uncertainty may destroy the synchronization or even break it. Therefore,how to synchronize effective networks with unknown parameters is an important problem for theoretical researches and practical applications. The outer synchronization of regular coupled networks with uncertain parameters has been widely studied[18]. However,no research for the outer synchronization of irregular coupled networks with uncertain parameters has been found. Specifically,small-world networks are a typical kind of irregular networks,which are ubiquitous in many real world problems[19]. The outer synchronization of small-world networks with uncertain parameters has not been treated.
For the systems with matched uncertainties,the asymptotical stability can be achieved via the sliding mode control technique. Since the publication of the survey paper[20] in 1977, significant interest on sliding mode control has been aroused in electrical engineering,aircraft, chemical reactors and so on. The process of sliding mode control aims to utilize a discontinuous control law to force the system state trajectories onto some predefined sliding surfaces,on which the system can desire properties such as stability,insensitivity to system parameter variations,disturbance rejection capability,and tracking ability. Recently,due to the potential applications,this technique has been widely used in the chaos synchronization between two chaos systems with uncertainties[21]. However,no work about the use of the sliding mode control technique has been found in synchronizing two complex dynamics networks with uncertainties. The present work aims to study the regular coupled networks with uncertain parameters or the irregular coupled networks with certain parameters. The rest of this paper is organized as follows. Section 2 states the outer synchronization problem of two Newman and Watts smallworld networks with uncertainties. In Section 3,based on the sliding mode control strategy,a switching surface and several control inputs are designed to ensure that the sliding condition is satisfied. An adaptive law is presented to estimate the switching gain. Section 4 presents two numerical examples to demonstrate the theoretical results. Section 5 ends the manuscript with concluding remarks. 2 Problem formalization
Consider a dynamical network consisting of N linearly coupled identical nodes,whose state equations are written as follows[22]:
where xi(t) = (xi1(t),xi2(t),· · · ,xin(t))T ∈ Rn is the state vector of the ith node. F : Rn → Rn is a smooth nonlinear vector field.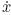 i(t) = F(xi(t)) is the node dynamical function. H : Rn →
Rn is a constant matrix linking the coupled variables and denoting the inner coupling functions
of the connected nodes. ξ > 0 is the relative weight of the coupling strength among the nodes of
the network,and A = (aij) ∈ Rn×n represents the coupling configuration of the network. This
work only treats symmetric coupling and diffusive coupling. Assume that A is a symmetric and
irreducible coupling matrix,and the diagonal elements of A satisfy
The off-diagonal elements aij (i,j = 1,2,· · · ,N; i ≠ j) of A are either 1 or 0. If there exists a
connection from node i to node j (j ≠ i),then set aij = aji = 1; otherwise,set aij = aji = 0.
Here,we select the Newman and Watts small-world network model as an example to study.
i(t) = F(xi(t)) is the node dynamical function. H : Rn →
Rn is a constant matrix linking the coupled variables and denoting the inner coupling functions
of the connected nodes. ξ > 0 is the relative weight of the coupling strength among the nodes of
the network,and A = (aij) ∈ Rn×n represents the coupling configuration of the network. This
work only treats symmetric coupling and diffusive coupling. Assume that A is a symmetric and
irreducible coupling matrix,and the diagonal elements of A satisfy
The off-diagonal elements aij (i,j = 1,2,· · · ,N; i ≠ j) of A are either 1 or 0. If there exists a
connection from node i to node j (j ≠ i),then set aij = aji = 1; otherwise,set aij = aji = 0.
Here,we select the Newman and Watts small-world network model as an example to study.
In fact,some general chaotic systems can be decomposed into such a form. Thus,(1) can be rewritten as
where γi is the parameter of the ith node. We set the network as (1),which consists of N linearly coupled identical nodes,i.e.,γi = γ1 = γ2 = · · · = γN.Take the network given by (3) as the drive network. Then,the response network with an adaptive control scheme can be given by
where yi(t) = yi1(t),yi2(t),· · · ,yin(t))T ∈ Rn is the state vector of the ith node of the response network.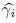 is the uncertain parameter of the ith node dynamics. dij has the same meaning as
aij in (1). ui(t) = (ui1(t),ui2(t),· · · ,yin(t))T is the adaptive controller of the ith node to be
designed.
is the uncertain parameter of the ith node dynamics. dij has the same meaning as
aij in (1). ui(t) = (ui1(t),ui2(t),· · · ,yin(t))T is the adaptive controller of the ith node to be
designed.
Consider (3),(4),and the configurationmatrices satisfying A 6= D. Then,the error equations of the drive-response network can be described by
Substituting (3) and (4) into (5) yields the error derivative as follows: The task is to design an appropriate controller so that the drive-response dynamical networks can achieve synchronization,i.e.,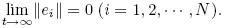 3 Sliding mode controller
3 Sliding mode controller
In this section,an adaptive sliding mode controller is designed to synchronize the driveresponse networks with uncertain parameters. This method involves the following two basic steps[17]:
(i) Select an appropriate switching surface for the desired sliding motion.
(ii) Establish a robust control law,which can guarantee the existence of the sliding manifold si(t) = 0,even with unknown parameters.
Firstly,design the switching function si(t) as follows[23]:
where φi is the function to be determined whose variables are the errors between the state variables of the chaotic systems at the ith node,and
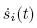 = 0 must be met when the
sliding surface moves. From (7) and (8),we have
when t → ∞,ei(t) → 0,and the sliding designed surface is asymptotically stable.
= 0 must be met when the
sliding surface moves. From (7) and (8),we have
when t → ∞,ei(t) → 0,and the sliding designed surface is asymptotically stable.
Then,the equivalent control law can be derived as follows:
To design the reaching mode control scheme,which can drive the states onto the sliding surface, we choose the following reaching law: where βsi is the reaching gain. The derivative of βsi can be achieved by the following adaptive
Finally,the switching control action can be defined as follows:
Under the condition,the drive network (3) and the response network (4) can realize synchronization by using the following adaptive control scheme: where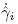 is the parameter estimate for the unknown parameter
is the parameter estimate for the unknown parameter 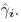
Theorem 1 For the drive-response complex networks given in (3) and (4),if the control input ui is defined by (12),then the trajectory of the error equation (5) converges to the sliding manifold si(t) = 0.
Proof Select the following Lyapunov candidate[24]:
Calculating the derivative of (14) along the trajectories of (7) and switching the control action (12),we obtain Substituting the adaptive control law (13) into (15) yields Let
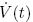 ≤ 0 when
≤ 0 when 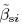 < 0,i.e.,ei(t) → 0. This completes the proof of the theorem.
4 Numerical examples
< 0,i.e.,ei(t) → 0. This completes the proof of the theorem.
4 Numerical examplesTo illustrate the effectiveness of the controller designed in the previous section,two numerical examples are presented. Consider the drive-response networks consisting of N linked identical Lorenz systems with different initial conditions. Let the sample period t be 0.001. Then,the node dynamics can be described by[25]
where





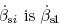 = 10.
= 10.
Case 1 Let


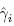 for the response network is defined
by
for the response network is defined
by

Figures 1-2 demonstrate the synchronization of the drive network and the response network with the Newman and Watts small-world network configuration,respectively. The results show that both the accumulated error and the parameter estimated error decrease gradually to zero. After a short transient time,the error curves become very smooth with no sudden error signal increase or paroxysmal intense oscillation. All uncertain parameters of the response network are accurately identified. It indicates that the outer synchronization can be achieved in spite of the network size,the nonidentical topological structure,and the differential initial conditions.
 |
| Fig. 1 Accumulated error e in Case 1 |
 |
| Fig. 2 Estimated error eγ in Case 1 |
Case 2 Let

In Figs. 3-4,the accumulated error and the estimated error tend asymptotically to zero after a short transient. All uncertain system parameters are accurately identified. It indicates that the outer synchronization can be achieved although the connection probability of the driveresponse networks is different.
 |
| Fig. 3 Accumulated error e in Case 2 |
 |
| Fig. 4 Estimated error eγ in Case 2 |
The results show that the outer synchronization is more general and more applicable than the inner synchronization. 5 Conclusions
The outer synchronization between two dynamical networks with nonidentical topological structures and uncertain parameters is theoretically and numerically investigated. A novel adaptive controller and several parameter identification criteria ensuring the synchronization are derived from the Lyapunov stability theory and the sliding mode control scheme. The Newman and Watts small-word network model with an uncertain Lorenz system is treated in the numerical examples with different initial conditions. The results show that the outer synchronization is general and applicable for both the drive network and the response network with the same or different connection probabilities.
| [1] | Estrada, E., Hatanoe, N., and Benzi, M. The physics of communicability in complex networks. Physics Reports, 514, 89-119 (2012) |
| [2] | Watts, D. J. and Strogatz, S. H. Collective dynamics of small-world networks. nature, 393, 440- 442 (1998) |
| [3] | Newman, M. E. and Watts, D. J. Renormalization group analysis of the small-world network model. Physics Letters A, 263, 341-346 (1999) |
| [4] | Cao, J., Wang, Z., and Sun, Y. Synchronization in an array of linearly stochastically coupled networks with time delays. Physica A, 385, 718-728 (2007) |
| [5] | Wang, Z., Duan, Z., and Cao, J. Impulsive synchronization of coupled dynamical networks with nonidentical duffing oscillators and coupling delays. Chaos, 22, 013140 (2012) |
| [6] | Yang, X., Cao, J., and Lu, J. Synchronization of Markovian coupled neural networks with nonidentical node-delays and random coupling strengths. IEEE Transactions on Neural Networks, 23, 60-71 (2012) |
| [7] | Cao, J., Alofi, A., Al-Mazrooei, A., and Elaiw, A. Synchronization of switched interval networks and applications to chaotic neural networks. Abstract and Applied Analysis, 2013, 940573 (2013) |
| [8] | Wang, X. F. and Chen, G. Complex networks: small-world, scale-free and beyond. IEEE Transactions on Circuits and Systems, 3, 6-20 (2003) |
| [9] | Chai, Y., Lü, L., and Zhao, H. Lag synchronization between discrete chaotic systems with diverse structure. Applied Mathematics and Mechanics (English Edition), 31(6), 733-738 (2010) DOI 10.1007/s10483-010-1307-7 |
| [10] | Guo, J. A difference equation approach to statistical mechanics of complex networks. Applied Mathematics and Mechanics (English Edition), 30(8), 1063-1068 (2009) DOI 10.1007/s10483- 009-0813-6 |
| [11] | He, G. and Luo, M. Dynamic behavior of fractional order Duffing chaotic system and its synchronization via singly active control. Applied Mathematics and Mechanics (English Edition), 33(5), 567-582 (2012) DOI 10.1007/s10483-012-1571-6 |
| [12] | Song, Q., Cao, J., and Liu, F. Synchronization of complex dynamical networks with nonidentical nodes. Physics Letters A, 374, 544-551 (2010) |
| [13] | Yang, X., Cao, J., and Lu, J. Stochastic synchronization of complex networks with nonidentical nodes via hybrid adaptive and impulsive control. IEEE Transactions on Circuits and Systems, 59, 371-384 (2012) |
| [14] | Wang, G., Cao, J., and Lu, J. Outer synchronization between two nonidentical networks with circumstance noise. Physica A, 389, 1480-1488 (2010) |
| [15] | Tang, H., Chen, L., Lu, J., and Tse, C. K. Adaptive synchronization between two complex networks with nonidentical topological structures. Physica A, 387, 5623-5630 (2008) |
| [16] | Wu, X., Zheng, W. X., and Zhou, J. Generalized outer synchronization between complex dynamical networks. Chaos, 19, 013109 (2009) |
| [17] | Li, R., Duan, Z., and Chen, G. Global synchronization of drive-response dynamical networks subject to input nonlinearity. Journal of Physics A: Mathematical and Theoretical, 41, 385103 (2008) |
| [18] | Yang, L. and Jiang, J. Adaptive synchronization of drive-response fractional-order complex dynamical networks with uncertain parameters. Communications in Nonlinear Science and Numerical Simulation, 19, 1496-1506 (2013) |
| [19] | Wang, X. F. and Chen, G. Synchronization in small-world dynamical networks. International Journal of Bifurcation and Chaos, 12, 187-192 (2002) |
| [20] | Utkin, V. Variable structure systems with sliding modes. IEEE Transactions on Automatic Control, 22, 212-222 (1977) |
| [21] | Tavazoei, M. S. and Haeri, M. Synchronization of chaotic fractional-order systems via active sliding mode controller. Physica A, 387, 57-70 (2008) |
| [22] | Pecora, L. M. and Carroll, T. L. Master stability functions for synchronized coupled systems. Physical Review Letters, 80, 2109-2112 (1998) |
| [23] | Kuo, C. L. Design of a fuzzy sliding-mode synchronization controller for two different chaos systems. Computers and Mathematics with Applications, 61, 2090-2095 (2011) |
| [24] | Wu, X. and Lu, H. Outer synchronization of uncertain general complex delayed networks with adaptive coupling. Neurocomputing, 82, 157-166 (2012) |
| [25] | Lorenz, E. N. Deterministic nonperiodic flow. Atmospheric Sciences, 20, 130-141 (1963) |
 2015, Vol. 36
2015, Vol. 36




























