Shanghai University
Article Information
- Wancheng SHENG, Ying ZENG. 2015.
- Generalized δ-entropy condition to Riemann solution for Chaplygin gas in traffic flow
- Appl. Math. Mech. -Engl. Ed., 36(3): 353-364
- http://dx.doi.org/10.1007/s10483-015-1915-6
Article History
- Received 2014-04-14;
- in final form 2014-07-17
2. Department of Mathematics and Physics, Quzhou University, Quzhou 324000, Zhejiang Province, China
The macroscopic model of vehicular traffic was firstly started with the first-order fluid approximation of traffic flow dynamics proposed by Lighthill and Whitham[1] in 1955 and Richards[2] in 1956. Since then,many scholars have focused on this topic[3,4,5,6,7] . Aw and Rascle[5] replaced the space derivative of the “pressure” with a convective derivative in Ref. [6] to resolve the theoretical inconsistencies and constructed the Aw-Rascle model. The model in the conservative form is
where ρ is the density of the vehicle,and v is the velocity of the vehicle. The Aw-Rascle model is one of the main fluid dynamic models for the traffic flow. Sun[8] studied the Riemann problem and the interactions of elementary waves for the Aw-Rascle model. System (1) with the equation of state is called the Aw-Rascle traffic model with the Chaplygin gas dynamics. Sheng and Zhang[9] presented the Riemann solutions for the transportation equations of zero-pressure flow in gas dynamics,in which δ-wave and vacuum appeared. Li et al.[10] discussed the behavior of global solutions with random initial data for the zero-pressure flow. Guo et al.[11] studied the Riemann problems of the two-dimensional (2D) Euler equations for the Chaplygin gas. Wang and Zhang[12] studied the Riemann problem with the Delta initial data for one-dimensional (1D) Chaplygin gas Euler equations. Pan and Han[13] discussed the Aw-Rascle model with Chaplygin pressure,and obtained the solutions of the Riemann problems and the initial-boundary value problems. Li[14] studied the Riemann problem with the initial data containing Dirac Delta functions for the Chaplygin pressure Aw-Rascle traffic model. However,their solutions cannot be obtained by the disturbed method except the first case in their paper and do not satisfy the δ-entropy conditions.In this paper,the Riemann problem to the Aw-Rascle model in traffic flow is studied with the Delta initial data for the Chaplygin gas. A new Delta wave is defined in some solutions, which is called the primary Delta. This paper is organized as follows. In Section 2,we present some preliminaries for (1) and (2),and show the Riemann solutions of (1) and (2). In Section 3, we construct the Riemann solutions of (1) and (2) to the Aw-Rascle model in traffic flow with the Delta initial data for the Chaplygin gas and the solutions globally under the generalized Rankine-Hugoniot relations and the δ-entropy conditions,respectively,and define the primary Delta. 2 Preliminaries
In this section,we review the classical Riemann solutions[11] of (1) and (2) with the initial data
(ρ,v)(x,0) = (ρ±,v±),±x > 0,
where ρ± > 0,and v± > 0.System (1) is strictly hyperbolic with the following two eigenvalues:
λ1 = v − ρ−1,λ2 = v,
which are called the wave characteristic and the flow characteristic,respectively. The corresponding right eigenvectors arer1 = (1,−ρ -2)T,r2= (1,0)T. λi (i= 1,2) are linearly degenerated with ∇λi ·ri= 0 (i = 1,2).
Since (1) and (2) remain to be invariant under the self-similar transformation (x,t) →
(αx,αt),where α is a constant,we seek the self-similar solution (ρ,v)(ξ),where  . Then,
the Riemann problem turns into the boundary value problem at infinity,i.e.,
. Then,
the Riemann problem turns into the boundary value problem at infinity,i.e.,
For a bounded discontinuity at ξ = σ,the following Rankine-Hugoniot conditions hold:
where the jump quantity [q] = q+ − q−,and σ is the velocity of the discontinuity. From (5),we obtain two kinds of discontinuities,i.e.,the contact discontinuity and the shock wave through which the density ρ increases from left to right.We conclude that the rarefaction wave R coincides with the shock wave S in the phase plane (ρ,v). It is easy to see that the characteristic lines are straight on both sides of the discontinuity line and one family of the characteristic lines (λ1 = v - ρ−1 ) coincides with the discontinuous line on both sides.
For any point (ρ_,v_) in the phase plane (ρ > 0,v > 0),we draw a branch of the curve (4) and have two asymptotic lines which are v = v_ − ρ_−1 and ρ = 0. The half branch (ρ > ρ_) of the curve is compressively denoted by S. The other half branch is denoted by R. We also draw a branch of (6) for ρ > 0,which is a contact discontinuity denoted by J . Then,the first quadrant of the phase plane is divided into three regions,i.e.,I,II,and III,which are shown in Fig. 1. For any given (ρ+,v+) in the first quadrant,the Riemann solution is shown as follows:
 |
| Fig. 1 Wave curves in phase plane |
(i) (ρ+,v+) ∈ I : S + J ;
(ii) (ρ+,v+) ∈ II : R + J ;
(iii) (ρ+,v+) ∈ III: Delta wave,i.e.,Sδ wave.
When (ρ+,v+) ∈ I ∩ II,we get an intermediate state (ρ*,v*) to connect the two waves
When (ρ+,v+) ∈ III,which satisfiesv+ − ρ+−1 < v+ < v_ − ρ_−1 < v_,
the characteristics start from the origin overlap in the domain Ω (see Fig. 2). In this case,some singularities may appear[9] ,and the singularities cannot be a jump with finite amplitudes. That is to say,there is no piecewise smooth and bounded solution. Therefore,a solution containing a weighted δ-measure,i.e.,the Sδ wave supported on a line,must be constructed to establish the existence in a space of measurers from the mathematical point of view. |
| Fig. 2 Analysis of characteristics |
Let us consider the solution of (1) and (2) of the form
satisfying the initial conditions where x(t),ω(t),and vδ (t) denote the location,the weight,and the propagation speed of the Sδ wave,respectively,and v0 is undetermined. Therefore,we can assert that (9) is the solution of (1) and (2) if the following generalized Rankine-Hugoniot relations are satisfied: where the jump quantity [q] = q+ − q_. By a simple calculation,we have when [ρ] ≠ 0,and when [ρ] = 0.Moreover,we can justify that the Sδ wave satisfies the δ-entropy conditions as follows:
3 Riemann problem with Delta initial dataIn this section,we consider (1) with the following initial data:
where m0 > 0.Let us consider the solutions in the following form:
satisfying the following generalized Rankine-Hugoniot conditions: with the initial data Next,we solve (17) and (18). From (17),we have Multiplying the first equation of (19) by vδ and jointing the obtained result with the second one,we get From (20),we have From (17) and (18),we obtain where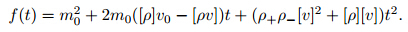
ƒ(t) > 0,t > 0.
From (19),we have
In particular,when m0 = 0,we have when [ρ] ≠ 0,and when [ρ] = 0. So far,we have completely constructed the solution (ω(t),vδ (t),x(t)) of (17) with (18),which has the following properties: When [ρ] ≠ 0, According to the relation among v_ − ρ_−1 ,v0,v_,and v+,we can construct the Riemann solutions of (1) and (15) in the following four cases:Case 1 v+ < v0 < v_ - ρ_−1 < v_.
Case 2 v0 < v_ -ρ_−1 < v+ < v_.
Case 3 v0 < v+ < v_ - ρ_−1 < v_.
Case 4 v_ -ρ_−1 < v0 < v+ < v_.
The other cases are similar.Case 1 v+ < v0 < v_ - ρ_−1 < v_
This is a typical case,in which the Sδ wave emits from the origin. It is easy to see that it satisfies the δ-entropy conditions. Solving (17) and (18),we obtain
where ω(t),vδ (t),and x(t) are defined as (22) and (23). By a simple calculation,we have The solution is shown in Fig. 3. |
| Fig. 3 Solution of Case 1 |
Case 2 v0 < v_ - ρ_−1 < v+ < v_ In this case,we cannot construct the solution as above. We need to construct the solution between a free boundary,i.e.,a new Delta wave,and the right contact discontinuity J (ρ+,v+).
Definition 1 A discontinuous curve x = x(t) is called the primary Delta wave in the solution denoted by Sδ if it satisfies the following conditions:
(i) The initial data contain a Delta distribution;
(ii) The solution on x = x(t) satisfies the generalized Rankine-Hugoniot relations and the generalized δ-entropy conditions that Sδ contacts with one or two families of characteristics on one or both sides of it.
According to the definition,we can seek the solution in the following form:
where (ρ*,v*)(x,t) =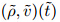 along the straight line
along the straight line 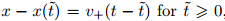 ,which is
also denoted as (ρ*,v*)
,which is
also denoted as (ρ*,v*)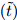 . (ρ*,v*)
. (ρ*,v*)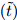 is the right state of the primary Sδ
wave,satisfying
and the primary Sδ wave satisfies the following generalized Rankine-Hugoniot conditions:
where [ρ] = ρ*(t) − ρ_ with the initial data
is the right state of the primary Sδ
wave,satisfying
and the primary Sδ wave satisfies the following generalized Rankine-Hugoniot conditions:
where [ρ] = ρ*(t) − ρ_ with the initial data
From (31) and (32),we obtain
From the above equations,we have Integrating (35) from 0 to t,we have Combining the first equation of (34) with (36),we get Solving (37) with ω(0) = m0 ,we have where α = ρ−m0(v_ - v0) > m0. From (38),we have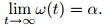
From (37),we obtain
Let F (t,ω) = ω − m0 + α ln(α − ω) − α ln(α − m0) + t. Then,we have
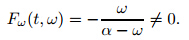
 |
| Fig. 4 Solution of Case 2 |
Case 3 v0 < v+ < v_ - ρ_−1 < v_
In this case,we construct the solution according to Definition 3.1 as in Case 2. The form of the solution is the same as that of (30) and (32). The solution on the right state of the primary Delta wave Sδ is
From v+ < v_ - ρ_−1,we have
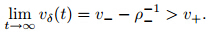
When t > t,we can construct the solution as that in Case 1,which is expressed in (22) and (23). The solution is shown in Fig. 5.
 |
| Fig. 5 Solution of Case 3 |
Case 4 v_ - ρ_−1 < v0 < v+ < v_ In this case,according to Definition 3.1,the new primary Delta wave Sδ must contact with the characteristics on both sides. We seek the solution in the following form:
where (ρ1,v1) and (ρ2,v2),which will be undetermined,are the left state and the right state of the primary Sδ wave,respectively,satisfying and the generalized Rankine-Hugoniot conditions with the initial data From (46) and (47),we have By a simple calculation with (48),we obtain Then,we get It is easy to see that ω(m0) = 0,which means that the weight of the primary Sδ wave disappears as t1 = m0. Because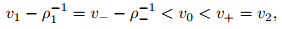
 |
| Fig. 6 Solution of Case 4 |
Remark 1 It can be easily checked that the solution is stable under perturbation on the initial data by the method in Refs. [12] and [15].
| [1] | Lighthill, M. J. and Whitham, G. B. On kinematic waves. II: a theory of traffic flow on long crowded roads. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sci- ences, 229A, 317-345 (1955) |
| [2] | Richards, P. Shock waves on the highway. Operations Research, 4, 42-51 (1956) |
| [3] | Payne, H. J. Models of Freeway Traffic and Control, Simulation Councils, San Diego, 51-61 (1971) |
| [4] | Whitham, G. B. Linear and Nonlinear Waves, Wiley InterScience, New York, 75-102 (1974) |
| [5] | Aw, A. and Rascle, M. Resurrection of second order models of traffic flow. Journal on Applied Mathematics, 60, 916-938 (2000) |
| [6] | Daganzo, C. F. Requiem for second-order fluid approximation of traffic flow. Transportation Research: Part B, 29, 277-286 (1995) |
| [7] | Colombo, R. M. Hyperbolic conservation laws in traffic flow. Journal on Applied Mathematics, 63, 708-721 (2002) |
| [8] | Sun, M. N. Interactions of elementary waves for the AW-Rascle model. Journal on Applied Math- ematics, 69, 1542-1558 (2009) |
| [9] | Sheng, W. C. and Zhang, T. The Riemann problem for the transportation equations in gas dynamics. Memoirs of the American Mathematical Society, 137, 1-77 (1999) |
| [10] | Li, J. Q., Zhang, T., and Yang, S. L. The Two-Dimensional Riemann Problem in Gas Dynamics, Chapman and Hall/CRC, New York, 38-66 (1998) |
| [11] | Guo, L. H., Sheng, W. C., and Zhang, T. The two-dimensional Riemann problem for isentropic Chaplygin gas dynamic system. Communications on Pure and Applied Analysis, 9, 431-458 (2010) |
| [12] | Wang, Z. and Zhang, Q. L. The Riemann problem with Delta initial data for the one-dimensional Chaplygin gas equations. Acta Mathematica Scientia, 32, 825-841 (2012) |
| [13] | Pan, L. J. and Han, X. L. The Aw-Rascle traffic model with Chaplygin pressure. Journal of Mathematical Analysis and Applications, 401, 379-387 (2013) |
| [14] | Li, J. Y. The Riemann problem with the Delta initial data for the Chaplygin pressure Aw-Rascle traffic model (in Chinese). Advances in Apllied Mathematics, 2, 114-126 (2013) |
| [15] | Chang, T. and Hsiao, L. The Riemann Problem and Interaction of Waves in Gas Dynamics, John Wiley and Sons, New York, 95-161 (1989) |
 2015, Vol. 36
2015, Vol. 36
























































