1 Introduction

In recent years,many powerful methods have been developed to construct the exact solutions of nonlinear partial differential equations (PDEs),e.g.,Tanh method ^[1] ,Lie symmetry method^[7] ,Lie algebra ^[8] ,conservation laws ^[2] ,and Hirota’s method ^[9] . Among these methods,the Lie symmetry method has been widely used in the diverse fields of mathematics and mechanics and almost all areas of theoretical physics^[10] . Suppose thattandxare two independent variables,uis a dependent variable,and u (l) denotes the set of all the partial derivatives of the orderl for u.Annth-order PDE

is invariant under the one-parameter Lie group of infinitesimal transformations in (t,x,u),which are given by with the associated infinitesimal generator if and only if where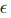 is the group parameter, 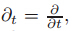andX ⁽ⁿ⁾ is the nth-order prolongation of X ^[11] .The above equation (6) yields an overdetermined and linear system for the infinitesimals ξ(t,x,u), τ(t,x,u),and η(t,x,u).

Once a symmetry group is known,the reduction of the equation can be obtained by solving the invariant surface condition

with the characteristic method. This typically yields u(t,x)=φ(t,x,W(z(t,x))),where φ and z are known functions. Substituting this into (7) will yield an ordinary differential equation for W,which is a function of z.

There are several generalizations of the classical Lie group method for symmetry reductions. Bluman and Cole ^[12] proposed the so-called nonclassical method of group-invariant solutions. In this method,(1) is augmented with (7). If the simultaneous solutions of (1) and (7) are invariant under the transformation (4),an overdetermined and nonlinear system of equations can be obtained for the infinitesimals τ,ξ,and η.

It is well-known that many physical models can be described by (1) with several parameters. For these parameters,it is necessary to know what symmetries the equation admits. Therefore, it is significant to perform symmetry classifications for the PDFs. LetG_Ebe the Lie symmetries of (1) with several arbitrary elements. LetG_E0be the kernel symmetry.It is the intersection ofG_E,and is admitted by (1) for any arbitrary element. Since G_E0⊂G_Efor every element, each symmetryG_Eis an expansion of G_E0. Hence,the symmetry classification is to find the kernel symmetry and all expansions of the kernel symmetry.

In this paper,we perform classical and nonclassical symmetry classifications of a class of general wave equations as follows

where f(u),g(u),and h(u) are smooth functions of their arguments. In order to exclude the trivial case,we consider the case g' (u)· h(u) ≠= 0. This PDE is important due to its direct relation to the equations from one-dimensional gas flow,shallow water wave theory,and electromagnetic transmission lines. Such equations include some celebrated equations,e.g., the telegraph equation ^[13] u_tt +(a+b)ut +abu=c ² u_xx and the Klein-Gordon equation ^[14] u_tt−u_xx+αu+βu ³ =0. Inthecase f(u)=0 and g(u) = 1,the generalized Klein-Gordon equation u_tt =u_xx+h(u) can be obtained from (8). Azad et al. ^[15] gave a complete symmetry classification for such equations. Temuer et al. ^[16] considered its nonclassical symmetry. When f(u)=0and h(u) = 0,(8) becomes the quasi-linear hyperbolic equation uu_tt =[F(u)u_x]_x, whose classical symmetry was considered in Ref. ^[17] and nonclassical symmetry was studied in Ref. ^[18]. In Refs. ^[19] and ^[20],a potential symmetry classification of the nonlinear wave equationuu_tt =[F(u)u_x]_x was considered. When f(u)=0,g(u) = 1,andh(u)=−sinu, (8) is the Sine-Gordon equation In 1939,Frenkel and Kontorova ^[3] studied the propagation of a slip in an infinite chain of elastically bound atoms lying over a fixed lowerchain with similar atoms. To describe this effect,they obtained a different differential equation,which could be approximated as the SineGordon equation. Under the traveling wave translation x' =1/2(x+t)andt' =1/2(x−t),(9) becomes the semi-linear wave equationu x' t' =sinu. For this equation,Pucci and Salvatori ^[9] considered the group properties,and Tsyfra ^[yes] considered the nonclassical symmetry. Summing up the above contents,the mathematical and physical model of (8) has a general representation. To our knowledge,however,its symmetry classification problem has not yet been studied so far.

Note that the point transformations

for any constants α,β,γ,and ρ_i (i=1,2,3) are equivalent transformations of (8),i.e.,(8) is invariant under the transformations such as

where

According to the equivalent transformations,we can use the canonical forms of f(u),g(u),and h(u) by scaling inf(u),g(u),h(u),u,and the translation inufor the classification computations.

The layout of the paper is as follows. In Section 2,the complete classical symmetry classification of (8) is given. In Section 3,a nonclassical symmetry classification of (8) with the arbitraryf(u),h(u),and g(u)=u μ is given. In Section 4,some exact solutions of (8) for specialf(u),g(u),and h(u) are given by the obtained classical and nonclassical symmetries. In Section 5,some concluding remarks are given. 2 Classical symmetry classification of (8)

For the classical symmetry classification of (8),we have the following theorem.

Theorem 1 All possible maximal algebras of the invariance of(8)for any fixed triplet of g(u),f(u),andh(u)are presented in Table 1. The generators of the Lie symmetry that appears in Table 1are given as follows:

Proof According to the classical Lie symmetry theory ^[yes] ,the invariance of (8) under the Lie symmetry group with the infinitesimal generator

yields the following determining equations: The problem of the classical symmetry classification is equivalent to exactly solving (12)-(16). The procedure of the classification is to find the kernel symmetry and its extensions.

(i) Kernel symmetry The kernel symmetry of (8) corresponds tof(u),g(u),and h(u). It is easily seen that if one off(u),g(u),andh(u) is an arbitrary function,thenη=τt =ξx= 0. It yields the kernel symmetry with the generators∂t and∂xforf(u),g(u),andh(u). Thus,wehaveprovedCase1 in Table 1.

(ii) Extensions of the kernel symmetry

With the specializations off(u),g(u),andh(u),we can obtain the extensions of the kernel symmetry. From (12),we have

If η= 0,it returns to the kernel symmetry case. Therefore,we only consider η≠=0inthe following process.

Solving (14),we can get two classes of canonical solutions for g(u) as follows:

where δ=±1. In the following,we consider each case of (18),respectively.

Case (C1) From (14),we have

Thus,(13) becomes

From the above equation,we can obtain four classes of canonical solutions for f(u) as follows: In the following,we consider each subcase of (20),respectively.

Subcase (C1.1) Substituting (19) and f(u) in Subcase (C1.1) into (13) yields ξ=b_1x+b₂. Then,(14) and (15) are automatically satisfied,and (13) and (16) become

It is verified that there is no solution for the above equations for μ=−4 or λ≠1/(2μ). If λ=1/(2μ)andμ≠−4,we have Therefore,Case 2 in Table 1 is obtained.

Subcase (C1.2) From (13) and (15),we have

Solving (16) yields which yields Case 3 in Table 1.

Subcase (C1.3) Solving (13),(15),and (16),we can obtain six classes of solutions for (12)-(16) as follows:

The above solutions yield Cases 4-9 in Table 1.

Subcase (C1.4) Solving (13),(15),and (16) yields the solutions (26),(27),and (29) and the following additional solutions:

Thus,Cases 6-7 and 9-14 in Table 1 are obtained.

Case (C2) Solving (14) and (15) yields

Then,(13) becomes From the above equation,we can obtain three classes of canonical solutions off(u) as follows: Similarly,we can obtain Cases 15-20 in Table 1,corresponding to Cases (C2.1),(C2.2),and (C2.3). Therefore,we complete the proof of the theorem. 3 Nonclassical symmetry classification of (8)

For equations such as (8) and the equations involving the Laplace operator,the analysis of the associated overdeterminedsystems for nonclassical symmetry is currently intractable. Since the determining equation is highly nonlinear and complexly coupled,it is hard to get the complete solution of the system in general cases of f(u),g(u),andh(u). Therefore,we consider a special physical case g(u)=u ^μ with the particular manageable generator

FromTable 1,wecanseethatallclassicalsymmetriesshow η_uu = 0. Thus,to obtain the nontrivial nonclassical symmetry,we only consider the case of η_uu≠ 0. All these restrictions do not lose the sense of obtaining the nonclassical symmetry for a class of (8).

Theorem 2 The equation

admits the nonclassical symmetry generator if and only if the functions f(u),h(u),andη(t,x,u)are given in Table 2and ξ is a constant.

Proof According to the nonclassical symmetry concept ^[yes] ,we can obtain the determining equations of the coefficients for the generator (39) as follows:

From (40),we can obtain two classes of solutions as follows:

where φ₁ and φ₂ are arbitrary functions of their arguments as integral constants.

Let us consider Case (NC1) first. Equation (40) is to become a first-order linear ordinary differential equation off(u)when f(u) is not identically equal to a constant. To solve the ordinary differential equation,we consider two cases,i.e.,ξ≠0andξ=0.

(I) ξ≠0 After solving f' (u) with (41),the coefficient of f(u) and the inhomogeneous term should not include the variables t and x. Otherwise,the expression off(u) will includetandx. Therefore, we can prove thatφ₁ (t,x)and φ₂ (t,x) are constants. Then,we can obtain the solution of Case 1 in Table 2 by solving (41) and (42).

(II)ξ=0 We can prove thatφ₁ (t,x)and φ₂ (t,x) are constants,i.e.,φ₁ (t,x)=b₁ andφ₂ (t,x)=b₂. Integrating (42) with respect tou,we can get Case 2 in Table 2.

When f(u)=c,where c is an arbitrary constant,from (42),we can find that ϕ1(t,x)and ϕ2(t,x) are constants,i.e.,φ₁ (t,x)=b₁ andϕφ₁ (t,x)=b₂.If ξ= 0,from (41) and (42),we can obtain Case 2 in Table 2. Ifξ≠=0 and μ=−1/2,from (41) and (42),we can obtain Case 3 in Table 2. When ξ≠=0and μ≠=−1/2,there is no solution for (41) and (42).

Similar to Case (NC1),from (41) and (42),we can obtain the solutions of Cases 4 and 5 in Table 2forCase(NC2). 4 Some exact solutions of (8)

In this section,we give some exact solutions of (8) for some cases in Tables 1 and 2.

Example 1 Case 2 in Table 1

In this case,(8) admits the classical symmetry with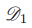. For the generator 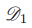,wehavethe

following similarity variables:

Therefore,the group-invariant solution of (8) is Substituting (44) into (8),with the corresponding g(u),f(u),andh(u)ofCase2inTable 1, we can reduce (8) to Solving (45) yields the following two classes of solutions: Therefore,the invariant solutions of (8) under the generator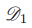 are as follows: The solution (48) is a quasi-period solution when

which indicates that the wave decays along the evolution of the timet. This property is shown in Fig. 1. The solution (49) is shown in Fig. 2.

Example 2 Case 3 in Table 1

For the generatorX1in Theorem 1,we have the following similarity variables:

Therefore,the group-invariant solution isω=v(ζ),i.e., Substituting (51) into (8),with the correspondingg(u),f(u),andh(u)of Case2 inTable 1, we can reduce (8) to where

It is hard to get an exact solution of this equation. A numerical solution of the above equation is given in Fig. 3.

Example 3 Case 1 in Table 2

As an example of the nonclassical symmetry reduction of (38),we solve (38),which corresponds to Case 1 in Table 2. In this case,(38) admits the nonclassical symmetry with

We take b₀ =0and a₀ =μ= 1 for simplicity. Then,the generator X has the following variables: Therefore,the group-invariant solution is ω=v(ζ),i.e., Then,we can reduce (38) to where ζ=x−t. Solving the above equation yields two classes of solutions as follows: Therefore,the invariant solutions of (38) under the nonclassical symmetry are

Example 4 Case 2 in Table 2

In this case,(38) admits the nonclassical symmetry with

We take b₁=c₀=0,b₂=1,and μ= 2 for simplicity. Then,the generatorXhas the following variables: Therefore,the group-invariant solution is ω=v(ζ),i.e., Then,we can reduce (38) to Solving the above equation yields the solution Therefore,the invariant solution of (38) is

It is worth mentioning that the solutions (57),(58),and (64) cannot be obtained from the classical symmetry reductions. 5 Conclusions

A complete classical symmetry classification and a nonclassical symmetry classification of the general wave equation (8) are given. Some exact solutions of the considered wave equation (8) for some particular cases are derived. The obtained results show that such nonlinear wave equations admit richer classical and nonclassical symmetries which are useful for solving the given equations.

Moreover,an interesting phenomenon has been found. The equation (38),corresponding to Case 2 in Table 2,includes an arbitrary functionf(u). From Theorem 1,the equation admits only the kernel symmetry. However,from Theorem 2,the equation also admits a nonclassical symmetry (59). This provides an additional way to solve the equation. The invariant solution of the equation under the nonclassical symmetry is given in Example 4. This is a solution of infinite equations corresponding to arbitrary f(u).