1 Introduction

A mass of residual rude oil will remain in the reservoir after the water-flooding technique is exploited because of the capillary force and the weakened displacement force due to the fluidity ratio between the displacement phase and the driven phase. It is very important to develop the displacement efficiency. A popular method is to add some chemical addition agents such as polymer,surfactant,and alkali into the injected mixture,which can improve the flooding efficiency. The polymer can optimize the fluidityof the displacement phase,modify the ratio with respect to the driven phases,balance the leading edges well,weaken the inner porous layer, and increase the efficiency of the displacement and the pressure gradient. Surfactant and alkali can decrease the interfacial tensions of different phases,and then make the bound oil move and gather ^{[1, 2, 3]} .

In view of the capillary force and immiscible and incompressible flow,in this paper,we discuss a second-order upwind fractional step difference method for the numerical simulation of the enhanced (chemical) oil production in porous media,and give a theoretical analysis. Based on the former mathematical and mechanical theory,we accomplish the software,and use it in the national oilfields such as Daqing Oilfield and Shengli Oilfield.

The mathematical model is a nonlinear coupled system with some initial-boundary values as follows ^{[1, 2, 3]} :

where X=(x1,x2,x3)^T ∈Ω,and t∈J=(0,T], where X∈Ω,and t∈J=(0,T],and whereX∈Ω,t∈J,andα=1,2,···,n_c. In the above equations,Ω is a bounded computational domain. Let the subscripts “o” and “w” denote the parameters of the oil phase and the water phase,respectively.φ is the rock porosity,κ(X) is the absolute permeability,and s_α=s_α(X,t) is the component concentration. The components denote the sorts of the chemical agents such as polymer,surfactant,and alkali,and the number is denoted bync. uis the Darcy velocity, K_α=K_α(X) is the diffusion coefficient,and Q_α is the source sink term related with the output. The rock void space is assumed to be full of water and oil,and c_o+c_w= 1. The capillary force depends on the concentrationc,i.e.,p_c(c)=p_o−p_w,where c=c_w=1−c_o.

The models (1) and (2) should be turned into a normal form ^{[1, 2]} .Letλ(c) denote the total migration rate of the two-phase fluid,and λ_l(c) denote the relative migration rate. They are defined by

The Chavent transformation ^{[1, 2]} yields the following flow equation by adding (1) and (2): where q=q_o+q_w. The concentration equation can be derived from the difference of (1) and (2) as follows:

where

Then,(1) and (2) can be rewritten as follows: It is clear that (6) and (7) can be restated as follows: where

It followsg(X,t,c)=λ_wq as q≥0. Therefore,g(X,t,c)=0 as q<0. Using (8),we can rewrite (3) as follows: whereX∈Ω,t∈J,andα=1,2,···,n_c. The following two different boundary value conditions are considered in this paper. (I) The boundary value condition for the constant pressure is where ∂Ω denotes the outer boundary surface of Ω.

(II) The boundary value condition for the no permeation case is

where γ denotes the outer normal unit vector. An additional condition is introduced to determine the pressurepin the no permeation case,i.e.,

The compatibility condition is

and the initial condition is

With an assumption of the periodic condition,Douglas and Russell^[4] ,Douglas ^{[5, 6]} ,and Ewing et al. ^[7] presented the finite difference method and the finite element method to analyze a type of two-dimensional incompressible two-phase displacement problems,and gave the theoretical error estimates. A combination method was discussed by combining the characteristic method with the normal finite difference method or the normal finite element method,which can reflect the hyperbolic nature of one-order part of the convection-diffusion equations and decrease the truncation error. This combination technique can also overcome numerical oscillation and dispersion,and can greatly improve the computational stability and accuracy. Douglas and Roberts ^[8] ,Yuan ^{[9, 10]} ,andEwing ^[11] presented mathematical models of slight compression, numerical method,and theoretical analysis for the two-dimensional compressible displacement problems under periodic conditions. Yuan ^{[12, 13, 14]} presented a new modified characteristic finite difference algorithm and a finite element algorithm,and derived the optimal order error estimates in the L 2 -norm,dropping the period condition. An interpolation computation was introduced to deal with the points along the characteristics lying outside the bounded domain. The characteristics intersected the grid boundary,and thus the corresponding values of the unknown function could be computed,which meant that the time step in the program design must vary due to the position of the grids nearby the boundary along the characteristics. In conclusion,actual computation is always complicated ^{[13, 14]} .

For parabolic equations,Axelsson and Gustafasson ^[15] ,Ewingetal. ^[16] ,andLazarovetal. ^[17] presented the upwind finite difference method. The proposed method can overcome the numerical oscillation and cancel the extra interpolation computation of the grids nearby the boundary along the characteristics. Peaceman ^[18] and Douglas and Gunn ^[19] used the upwind method in two-phase (water and oil) displacements successfully. However,it is hard to proceed the theoretical analysis. The stability and convergence are derived by the Fourier method only for constant coefficient cases,and this analysis is not generalized for variable coefficient equations ^{[19, 20, 21]} . Considering actual applications and numerical stability and accuracy,here we present a secondorder upwind fractional step finite difference method for the three-dimensional incompressible and immiscible two-phase displacement coupled problem of enhanced oil production,considering the capillary force. This algorithm can overcome the numerical oscillation and dispersion, and decrease the computational scale by decomposing the three-dimensional problem into three successive one-dimensional subproblems. Using the calculus of variation,the energy analysis method,the commutativity of the products of the difference operators,the decomposition of high-order difference operators,and the theory of a priori estimates,we give the second-order convergence result of accuracyand the error estimates in thel 2 -norm,and successfully solve the international problem of Douglas and Ewing. The method discussed in this paper has been successfully used in the numerical simulation of enhanced oil production ^{[1, 2, 3]} .

In general,the problem is positive definite,i.e.,

where a _∗,a ^∗ ,φ_∗,φ ^∗ ,D_∗,D^∗,K^∗ ,andA^∗ are all positive constants.b(c),g(c),andQ_α(c,sα) are Lipschitz continuous in theε0neighbors of the solutions. The exact solutions of (8)-(14) are assumed to be suitably smooth,i.e.,

2 Second-order implicit upwind fractional step finite difference method

Let the partition Ω_h replace the domain Ω shown in Fig. 1.

This paper only discusses the problem with constant pressure boundary values. The analysis can be used in the problem with no-flow boundary values after slight modification. Let h₁,h₂, and h₃denote the different spacial steps in thex1-axis,the x₂-axis,and the x₃-axis,respectively. x_1i =ix₁,x_2j =jh₂,and x_3k=kh₃.

Let∂Ω_hrepresent the boundary of Ω_h.Let

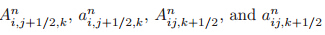where the signsAn can be defined analogously. Let Then,the finite difference algorithm of (8) is given by where

In the above expression,Q_h denotes the cube of the three side-lengthsh1,h2,andh3centered at the origin. Approximate the Darcy velocity Uⁿ⁺¹ =(U₁ ⁿ⁺¹ ,U₂ ⁿ⁺¹ ,U₃ ⁿ⁺¹ ) ^T as follows:

Then,the values of U_2,ijk ⁿ⁺¹ and U_3,ijk ⁿ⁺¹ can be obtained similarly.

Consider the implicit upwind fractional step scheme of the saturation (9). If c ⁿ is given,it is necessary to find c ⁿ⁺¹ at the (n+ 1)th step. With the approximation,the differential operator can be replaced by the difference quotient

Then,(9) can be rewritten as follows: where u=(u₁,u₂,u₃) ^T . The second-order implicit upwind fractional step program is stated by where

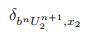and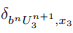 are defined analogously,and

Let

Let there be an implicit upwind fractional step algorithm for the component concentration equation (10). where

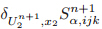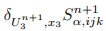and andare defined similarly The initial approximation is expressed as The implicit program runs as follows:

(i) Give {P _ijk ⁿ,C _ijk ⁿ ,S_{α, ijk}, ⁿ α =1,2,···,n_c},and compute the pressure {P _ijk ⁿ⁺¹ }by the elimination method or the conjugate gradient method from the difference equation (17).

(ii) Obtain the values of the Darcy velocity{u _ijk ⁿ⁺¹ }by (18).

(iii) Compute the solution of the transition sheaf{C _ijk ^n+1/3 }in thex1-direction by the speedup method from (20),proceed{C _ijk ^n+2/3 }in the x2-direction by (21),and obtain {C ⁿ⁺¹ _ijk }in the x3-direction by (22) similarly.

(iv) Compute{S_{α, ijk} ^n+1/3 }and{S_{α, ijk} ^n+2/3 }in the x1-andx2-directions by the speedup method from (23) and (24),and obtain the saturation {S ⁿ⁺¹ _{α, ijk} }by (25).

The program is accomplished in parallel with respect to α=1,2,···,n_c.Thesolutionsof (17),(20)-(22),(23)-(25),and (26) exist,and are solved based on the positive definite condition. 3 Convergence analysis

For convenience,in the theoretical analysis,the computational domain and some notations are taken as follows:

Letπ=p−P,ξ =c−C,and ζ_α=s_α−S_α,wherep,c,and s_α are the exact solutions of (8)-(13),andP,C,andSαare the numerical solutions of (17)-(26). Introduce the inner products and norms in L ² (Ω) and H¹ (Ω) ^{[22, 23]} as follows:

Theorem 1 Assume that the exact solutions of(8)-(13)are suitably smooth,i.e.,

Assume that the partition parameters satisfy Then,running(17)-(25)layer by layer yields where

and the constants are denoted by

Proof The flow equation (8) (t=t ⁿ⁺¹ ) subtracts the difference equation (17),and it gives rise to the error of the pressure,i.e., where

Multiplying both sides of (29) by π ⁿ⁺¹ and summing by parts yield

Then, The error estimates of the saturation are discussed later. Cancel C_ijk ^n+1/3 and C_ijk ^n+2/3 in (20)- (22),and let U ⁿ⁺¹ =b(C ⁿ )U ⁿ⁺¹ . For convenience,D(C ⁿ )≈D(X) in the next analysis,and the natural analysis in the numerical mathematics is the same. The above difference can be stated as follows: where

Basedon(9)(t=t ⁿ⁺¹ ),(32),and a new symbol Û ⁿ⁺¹=b(c ⁿ⁺¹ )u ⁿ⁺¹ ,the error equation of the saturation can be given by where

Testing the error equation (33) by ξ_ijk ⁿ⁺¹ Δtand making inner product and summation by parts yield An induction hypothesis is given by Consider the second term on the left-side of the above expression firstly,i.e.,

Then where

The right-side terms of (34) are estimated. By (31) and (35),we have

It is true for the second term on the right-side of (34) that

For the third term and the last term on the right-side of (34),by theε0-Lipschitz and (35), we can obtain

Then,the fourth term can be estimated as follows: For the terms of the above expression,we have

With the condition

the induction hypothesis (35),and the estimate (31),we have

Then, The other terms consisting of δ_x1 δ_x2 ξ ⁿ⁺¹ are as follows: The first term is firstly discussed,i.e.,

It is easy to see that

are bounded by the induction hypothesis and inverse theorem. Apply the Cauchy inequality Estimate the other terms of (42) in a similar fashion,i.e., Then,we can obtain the same result as (44) for the other parts of the fourth term. For the fifth,sixth,and seventh terms,from (27),(35),and the inverse estimates,we have Applying (36)-(47) to estimate (34) yields Summing (48) ontfor 0≤n≤Land noting thatξ ⁰ =0yield Using the Gronwall lemma,we have where

It remains to test the induction hypothesis (35). It is right asn= 0 becauseξ ⁰ =0. Assume that the induction hypothesis holds for any positive integernbetween 1 and a given positive integer l. From (31) and (50),we have

Then,from (27) and the maximum norm estimates,we have

Therefore,(35) holds whenn=l+1.

We go on to discuss the error estimates of the component concentrations. An equivalent expression is given after cancelingS ^n+1/3 _α and S ^n+2/3 _αfrom (23),(24),and (25) and introducing a new notation

where

Let

Then,from (10) (t =t ⁿ⁺¹ ) and (51),we can derive the error equation of the component concentration as follows: where

In the numerical analysis,there exists bound water almost everywhere in the oil reservoir, i.e.,there exists a positive number c_∗such thatc(X,t)≥c_∗>0. From (50),we can see thath and Δtare small enough so that the convergence result ofc(X,t) can be expressed as

Multiplying both sides of (52) by ζ_α,ijkΔt ⁿ⁺¹ ,making inner product,and giving a similar discussion,we can obtain This completes the proof. 4 Applications

The implicit upwind fractional step methodhas been successfully used in the software design of enhanced oil production such as polymer flooding and the numerical simulation and analysis of actual oil production in Daqing Oilfield. The mathematical model is formulated as follows ^{[1, 2, 3]} :

Let “w” and “o” refer to water and oil,respectively. φ is the porosity. The signs of the _lth phase are defined as follows:p_l is the pressure,s_l is the saturation,B_l isthevolumefactor,λ_l is the fluidity,γ_l is the proportion,ql is the source sink term,and pcis the pressure of capillary.

The mathematical model of the polymer and the motion of kation and anion components is described by a system of the convection-diffusion equations as follows:

wherecα=c_α(x,t)(α=1,2,···,nc) denote the concentrations of the components,and n_c is the number of the components. The simplified model of (55) and (56) is turned into the system of (8)-(13) ^{[1, 2, 24]} .

The experimental tests for Daqing Oilfield (the southern fifth development zone of the polymer flooding) are discussed by the polymer flooding software. The three-dimensional domain of the geological model is partitioned into 86×39×9 subdomains. The effective thicknesses of each layer are illustrated in Fig. 2,where the deeper the shaded areas are,the thicker the porous media are; the lighter the areas are,the thinner the media are.

The curve of the instantaneous oil production of the polymer in the southern fifth zone and the illustration of water moisture are shown in Figs. 3 and 4,respectively. The numerical data of the analysis of matter balance are given in Table 1. From the numerical data,we can easily find that the numerical method and the used software can keep high order of accuracy,and the numerical simulation can reflect correctly the physical process and the principle of the polymer flooding. Moreover,the main physical quantities are distributed reasonably,the computational accuracy is high,and some results of the polymer such as accumulation and endless loop do not arise.

Acknowledgements

The authors express their deep appreciation to Prof. J. DOUGLAS,Jr., Prof. R. E. EWING,and Prof. Lishang JIANG for their helpful suggestions in the serial of research of chemical production.