Shanghai University
Article Information
- Bo YANG, Weiqiu CHEN, Haojiang DING. 2015.
- Three-dimensional elastostatic solutions for transversely isotropic functionally graded material plates containing elastic inclusion
- J. Meteor. Res., 36(4): 417-426
- http://dx.doi.org/10.1007/s10483-015-1950-9
Article History
- Received 2014-07-16;
- in final form 2014-12-01
2. Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, China;
3. Department of Civil Engineering, Zhejiang University, Hangzhou 310058, China
Elastic response analysis of homogeneous plates inserted with an elastic circular inclusion is always one of important classical research topics in elasticity. For example,Muskhelishvili[1] , Savin[2] ,and Lekhnitskii[3] obtained a series of plane elasticity solutions and classical plate theory solutions by the complex variable method.
Functionally graded materials (FGMs) are a new type of inhomogeneous materials which can ensure the continuous distribution of stresses and thus avoid some problems appearing in conventional laminated materials,such as stress concentration and interfacial debonding. Therefore,FGMs have shown significant application prospects in many fields. Many theoretical studies have been carried out on static analysis of FGM plates. For instance,Ramirez et al.[4] obtained approximate static solutions for two types of FGM plates by a discrete layer model in conjunction with the Ritz method. Li et al.[5] derived the elasticity solutions for transversely isotropic FGM circular plates subject to axisymmetric transverse loads. Based on the fourthorder shear deformation plate theory,the axisymmetric bending of FGM circular plates subject to a uniform transverse load was studied by Sahraee and Saidi[6]. More recent works on FGM plate theories and their applications can be found in the review paper of Jha et al.[7].
It is noted that based on the three-dimensional (3D) theory of elasticity,Mian and Spencer[8] obtained a class of 3D solutions for isotropic FGM plates with tractions-free surfaces,in which the material properties were assumed to vary arbitrarily with the thickness-coordinate. Using the complex function theory,England[9] generalized Mian and Spencer’s method[8] to the case involving the effect of the top-surface pressure,which satisfies the biharmonic equation or higher-order ones. Hereinafter,this complex formulation will be referred to as the EnglandSpencer plate theory. With this formulation,England[10] studied the equilibrium problem of an isotropic FGM annular plate containing a rigid inclusion. Y ang et al.[11, 12] extended England’s method[9] to the transversely isotropic FGM plates and obtained the elasticity solutions of an FGM rectangular plate with opposite edges simply supported and subject to a special family of biharmonic polynomial loads (totally 12 different types) as well as those of an FGM annular plate subject to biharmonic loads under different boundary conditions.
To the best knowledge of the authors,no work is available in the literature on the subject of the equilibrium problem of an FGM plate containing an elastic circular inclusion. The purpose of this paper is to investigate 3D equilibrium problems of a transversely isotropic FGM plate containing an elastic inclusion based on the authors’ previous work[11, 12]. 2 England-Spencer plate theory
Consider a transversely isotropic FGM plate bounded by the planes z = ± h/2 in the Cartesian coordinates (x,y,z). The isotropic planes of the material are parallel with the xy-plane that coincides with the mid-plane of the plate and are perpendicular to the z -axis that is vertically upward. The plate is free from the shear tractions on the upper and lower surfaces and subject to a normal biharmonic pressure p (x,y) only on the upper surface. Thus,we have
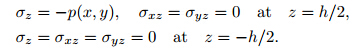
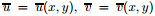 ,and
,and
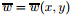 are the mid-plane displacements,and
The expressions of functions Rj (j = 0,1,· · · ,4) and Tk
(k = 1,2,· · · ,4) can be determined
by invoking the stress boundary conditions on the upper and lower surfaces of the plate,along with the following equations governing w(x,y) and Ω (x,y) = v,x − u,y:
where the expressions of constants k1,k2,k3,k4,S1(h/2),and S21 were given by Yang et al.[11].
are the mid-plane displacements,and
The expressions of functions Rj (j = 0,1,· · · ,4) and Tk
(k = 1,2,· · · ,4) can be determined
by invoking the stress boundary conditions on the upper and lower surfaces of the plate,along with the following equations governing w(x,y) and Ω (x,y) = v,x − u,y:
where the expressions of constants k1,k2,k3,k4,S1(h/2),and S21 were given by Yang et al.[11].
If p(x,y) = 0,Eqs. (4),(3),and (1) can be immediately simplified as
It is then shown that the mid-plane displacements and the resultant forces can be expressed as follows:
where α(ζ),β(ζ),φ(ζ),and ψ(ζ) are four analytic functions of the complex variable ζ,and a1,a2,a5,a6,a7,b1,b2,b5 ,b6,b7,and b8 are real constants that can be found in Ref. [11]. 3 FGM annular plateLet us consider an FGM annular plate with the inner radius a and the outer radius b,subject to the uniform radial forces Nra,Nrb and the uniform bending moments Mra,Mrb acting on the inner and outer cylindrical boundaries of the plate. This is an axisymmetric problem. We assume that the four analytic functions take the following simple forms:
where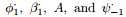 are real constants to be determined. Substituting Eq. (13) into
Eqs. (6) and (7) yields
are real constants to be determined. Substituting Eq. (13) into
Eqs. (6) and (7) yields
It can be found from Eq. (15) that
It is shown from Eqs. (14) and (16) that the four analytic functions in Eq. (13) do give rise to a state of axisymmetric deformation. Substituting Eq. (13) into Eqs. (8)-(10) and (12) yields
We obtain from Eqs. (17)-(19) that
The following conditions are satisfied on the cylindrical boundaries (r = a,b) of the annular plate:
Obviously,the last two equations in Eqs. (25) and (26) are automatically met. Substituting Eqs. (21) and (23) into the first two equations in Eqs. (25) and (26) yields
It can be found from Eqs. (27)-(30) that
whereBy substituting Eqs. (31) and (32) into Eqs. (21)-(24),we obtain
By substituting Eqs. (31) and (32) into Eqs. (16) and (14),we obtain 4 Three cases 4.1 FGM circular plate
We have r0 = 0 when a → 0. In this case,the annular plate becomes a circular plate with
radius b. It can be found from Eqs. (34)-(38) that
4.2 Infinite FGM plate with circular hole
We also have r0 = 0 when b → ∞. Then,the annular plate becomes an infinite plate with
a circular hole of a radius a. Let Nrb = 0 and Mrb = 0. We find from Eqs. (34)-(38) that
To investigate the problem of a plate containing an elastic inclusion,we propose to insert
an elastic inclusion of a radius a + ε into the hole of a radius a in the infinite plate. Here,ε
is a small quantity whose order is the same as some allowable displacement of the plate. The
friction between the inclusion and the plate is ignored. This is still an axisymmetric problem.
In the following,the physical quantities of the inclusion are distinguished by the superscript
(1) from those of the plate without any superscript. Thus,the radius of the elastic inclusion
becomes There are the resultant forces Nr0 and Mr0 acting on the interface between the inclusion and
the plate. Let r = a + ε,Nrb= Nr0 ,and Mrb = Mr0 in Eq. (40). Let r = a,Nra= Nr0,and Mra = Mr0 in Eq. (42). Equation (44) can be further expressed as
The resultant forces Nr0 and Mr0 can be solved from Eq. (45). Replacing the resultant forces
Nraand Mra with Nr0 and Mr0 in Eqs. (41) and (42),respectively,we can obtain the expressions
of the mid-plane displacements and the resultant forces of the infinite plate and further the 3D
displacement and stress fields.
5 Degeneration analysis
When the material of the elastic inclusion and the plate degenerates to the transversely
isotropic homogeneous one,we have
If the material is isotropic and homogeneous,we have
It can be found from Eq. (40) that
By taking
It can be found from Eq. (42) that
It can also be proved that the radial displacement given by Eq. (49) is identical to that
obtained by Muskhelishvili[1]
by letting µ = G and Nr0 / h = −P .
5.3 Infinite homogeneous plate containing elastic inclusion
Equation (45) can be rewritten as
By substituting Eq. (57) into Eq. (54),we obtain
The solution of this problem obtained by Muskhelishvili[1]
is as follows:
Since G = µ,G(1)
= µ0,v(1) = v0,a = R,and Nr0 = −P h,we can find that Eq. (58) gives exactly the same result as Eq. (60).
We finally note that Eq. (52) is the solution of an FGM plate,and Eq. (54) corresponds to
a homogeneous plate,for which Mr0 = 0,indicating that it is a plane stress problem.
6 Conclusion
Based on a generalization of the England-Spencer plate theory for a transversely isotropic
FGM plate,the elasticity solutions of FGM plates subject to loads applied on the cylindrical
boundaries of the plates for three different cases are obtained. They include a circular plate,
an infinite plate with a circular hole,and an infinite plate containing an elastic inclusion. In
the analysis,the material coefficients are allowed to vary arbitrarily in a continuous fashion
along the thickness of the plate. The analysis is based on the England-Spencer formulations
in terms of four analytic functions α(ζ),β(ζ),φ(ζ),and ψ(ζ). With these functions,the 3D
displacement and stress fields for a boundary-value problem are completely determined.
The obtained analytical solutions for the three considered cases exactly satisfy the equilibrium equations of the plate and the traction boundary conditions on the faces/interfaces of
the plate. Approximations are introduced only in the satisfaction of the boundary conditions
around the circumferential edge of the plate. The elasticity solutions of a transversely isotropic
(or isotropic) and homogeneous plate for the above three cases are also obtained through the
degenerate analysis.
Because no simplified hypotheses about the stress and displacement fields are introduced,
the present elasticity solutions can serve as a benchmark to access the validity and accuracy of
various simplified plate theories or numerical methods that may be used in the analysis of such
plates.
 ,and that of the plate is
,and that of the plate is  ,when the elastic inclusion is inserted into
the circular hole of the plate. Therefore,
,when the elastic inclusion is inserted into
the circular hole of the plate. Therefore,


| [1] | Muskhelishvili, N. I. Some Basic Problems of the Mathematical Theory of Elasticity, Noordholf, The Netherlands (1953) |
| [2] | Savin, G. N. Stress Distribution Around Hole, Pergamon Press, New York (1961) |
| [3] | Lekhnitskii, S. G. Anisotropic Plate, Gordon and Breach, New York (1968) |
| [4] | Ramirez, F., Heyliger, P. R., and Pan, E. Static analysis of functionally graded elastic anisotropic plates using a discrete layer approach. Composites: Part B, 37, 10-20 (2006) |
| [5] | Li, X. Y., Ding, H. J., and Chen, W. Q. Elasticity solutions for a transversely isotropic functionally graded circular plate subject to an axisymmetric transverse load qrk. International Journal of Solids and Structures, 45(1), 191-210 (2008) |
| [6] | Sahraee, S. and Saidi, A. R. Axisymmetric bending analysis of thick functionally graded circular plates using fourth-order shear deformation theory. European Journal of Mechanics-A/Solids, 28, 974-984 (2009) |
| [7] | Jha, D. K., Kant, T., and Singh, R. K. A critical review of recent research on functionally graded plates. Composite Structures, 96, 833-849 (2013) |
| [8] | Mian, A. M. and Spencer, A. J. M. Exact solutions for functionally graded and laminated elastic materials. Journal of the Mechanics and Physics of Solids, 46, 2283-2295 (1998) |
| [9] | England, A. H. Bending solution for inhomogeneous and laminated elastic plates. Journal of Elasticity, 82, 129-173 (2006) |
| [10] | England, A. H. Stiffness coefficients for inhomogeneous elastic plates. International Journal of Engineering Science, 47, 438-451 (2009) |
| [11] | Yang, B., Chen, W. Q., and Ding, H. J. Elasticity solutions for functionally graded annular plates subject to biharmonic loads. Archive of Applied Mechanics, 84(1), 51-65 (2014) |
| [12] | Yang, B., Ding, H. J., and Chen, W. Q. Elasticity solutions for functionally graded rectangular plates with two opposite edges simply supported. Applied Mathematical Modelling, 36, 488-503 (2012) |
 2015, Vol. 36
2015, Vol. 36






































