Shanghai University
Article Information
- Huiling ZHAO, Zhiming YE. 2015.
- Analytic elasticity solution of bi-modulus beams under combined loads
- J. Meteor. Res., 36(4): 427-438
- http://dx.doi.org/10.1007/s10483-015-1922-9
Article History
- Received 2014-07-07;
- in final form 2014-09-29
2. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China
There is a difference of the elastic modulus in tension and compression for bi-modulus materials. The value of elastic modulus of every point in the bi-modulus elastic body depends on not only the material itself but also the boundary conditions and the loads applied[1] . The studies on the criterion for elastic modulus with positive-negative signs are quite extensive[2, 3, 4, 5] . Beam is the most extensively used member in engineering practice. Ignoring the difference between the tensile modulus and compressive modulus causes errors in the solution of mechanic behavior of the beams with bi-modulus materials and may lead to undesirable engineering design. Yao and Ye[6] derived an analytical solution for a cantilever bi-modulus beam based on a plane-section assumption. He et al.[7] obtained an analytical solution for a simply supported bi-modulus beam under uniform loads. Wu et al.[8] presented an approximate solution for a cantilever bi-modulus beam subjected to linearly distributed loads by the Kantorovich variationly method. Yang et al.[9] obtained the bi-modulus cantilever beam elastic solutions by the semi-inverse method.
However,these solutions have certain limitations on accuracy,load patterns,and some specific conditions. This paper presents a simple approach to the general analytic solution of the statically determinate bi-modulus beams under various boundary conditions. The proposed methodology can obtain a more accurate solution without the plane-section assumption. 2 Determination of neutral surface
A general analytic model of a bi-modulus beam is shown in Fig. 1. As shown in Fig. 1(a), a Cartesian coordinate system is used in the model. The origin locates on the neutral surface, and the height of the beam cross section,h,is the sum of h1 and h2. Due to different tensile and compressive elastic moduli,h1 and h2 are not equal in value,whereas they are equal for the beam with the same modulus. h1 and h2 are unknown in the analytic model. Herein,the zone above the neutral surface,namely,the height from the origin to the top boundary,is named Zone 1,and the zone below the neutral surface,that is,the height from the origin to the bottom boundary,is named Zone 2. It will be found that which zone,Zone 1 or Zone 2,is the tensile zone from the solution hereinafter in this paper. The length of the beam is l,and the width of the beam cross section is 1. The transversely distributed load q(x) applies on the top boundary of the beam. The concentrated load P and the moment M are applied on the end locating at x = 0.
 |
| Fig. 1 Bi-modulus beams under combined loads |
In transverse bending beams,the cross section is unable to maintain the plane with warping caused by the shear stress,as shown in Fig. 1(b). A tiny hexahedron with the length as dx,the height as dy,and the width as 1 is taken from the beam to study the deformation,as shown in Fig. 1(c). Figure 1(d) shows the detail of the hexahedron in an enlarged scale.
It can be seen from Fig. 1(d) that the layer AB with the distance y to the neutral surface changes into the layer A1B1,and A1B1 = AB + BB1 − AA1,in which AA1 and BB1 are absolute displacements.
Based on Hook’s law for shear,we can obtain
where τxy is the shear stress,G is the shear modulus,and γxy is the shear strain. where ρ is the curvature of the deformed beam.The absolute elongation of the layer AB is given as
Then,the strain of the layer AB can be obtained by the following equation: The curvature of the deformed beam ρ is given as where E is the elastic modulus,A is the cross-sectional area of the beam,I is the inertia moment,and α is the shear shape coefficient of the cross section,which is 1.2 when the cross section is rectangular.According to Hook’s law,the bending stresses of Zone 1 and Zone 2 are presented as follows:
where Q is the shear force,E1 and E2 are the elastic moduli of Zone 1 and Zone 2,respectively,G1 and G2 are the shear moduli of Zone 1 and Zone 2,respectively,the inertia moment of Zone 1 is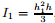 ,the inertia moment of Zone 2 is
,the inertia moment of Zone 2 is 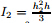 ,the static moment of Zone 1 is
,the static moment of Zone 1 is 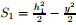 ,and the static moment of Zone 2 is
,and the static moment of Zone 2 is 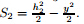 .
.
The force equilibrium equation in the x-direction is presented as follows:
The relationship between h1 and h2 derived from Eq. (7) is Making use of h1 + h2 = h,the value of h1 and h2 can be determined as 3 Stress function methodThe general stress function formula for the bi-modulus bending beam under combined loads is proposed in this section. Then,the analytic solution is derived based on the stress and force continuity conditions and the boundary conditions. The solution is general and has extensive applications in analyzing the mechanical behavior of bi-modulus beams. 3.1 General formula of stress function
According to the Saint-Venant principle,the bottom boundary (0 ≤ x ≤ l,y = −h2) and the top boundary (0 ≤ x ≤ l,y = h1) are the main boundaries. The surface force at the bottom boundary (0 ≤ x ≤ l,y = −h2) is zero,and the surface force at the top boundary (0 ≤ x ≤ l,y = h1) is − (ax + b).
The point,whose coordinate is (0,− h2),is defined as the starting point of the boundary. According to the mechanical sense of the stress function Φ and its derivative on the boundary, the values of the stress function Φ and its derivatives on the bottom boundary and the top boundary are presented as follows:
If the mechanical sense of the stress function Φ is applied on the beam with the bi-modulus material,the stress functions of Zone 1 and Zone 2 are given in the following formulae: where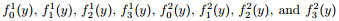 are unknown functions to be
determined.
are unknown functions to be
determined.
The force boundary conditions on the top boundary (0 ≤ x ≤ l,y = h1) and the force boundary conditions on the bottom boundary (0 ≤ x ≤ l,y = −h2) are obtained as follows:
The stress function should satisfy the compatibility equation. Therefore,the controlling equation can be derived as follows: Because arbitrary x in the beam span should satisfy the coefficient term,the free term of the controlling align shown as Eq. (13) should be zero as follows: The following equations are obtained by computing the integrals of Eq. (14): where C11,C21,· · · ,C161 and C12,C22,· · · ,C162 are the unknown constants to be determined by means of the stress and force continuity conditions and the boundary conditions.The stresses in the x-direction and the y-direction (σx and σy) and the shear stress τxy of Zone 1 and Zone 2 can be expressed as
According to the assumption proposed by Yao and Ye[6] ,the stress σx at the neutral surface y = 0 is zero. The stresses σx,σy,and τxy should maintain continuous. The equations are obtained as follows:
The continuous conditions for force and moment at the neutral surface y = 0 can be given as follows: By means of solving Eq. (12a),Eq. (17),and Eq. (18) simultaneously,the constants C11, C21,· · · ,C161 and C12,C22,· · · ,C162 are obtained and substituted into the stress functions of Zone 1 and Zone 2,which can be presented as follows: where nh is the ratio of h1 to h2. 3.2 Stress componentThe relationships between the stress components and the stress functions are defined as Eq. (16a) and Eq. (16b). By substituting the known stress functions Φ1 and Φ2 of Zone 1 and Zone 2 into this relationship,the stress components of Zone 1 and Zone 2 are expressed as follows:
As for the stress components of Zone 1 (0 ≤ y < h1),
As for the stress components of Zone 2 (−h2 ≤ y ≤ 0), where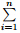 is the sum of the moments at a certain cross section caused by all the transverse
loads,n is the number of the transverse loads,and the inertia moments of Zone 1 and Zone 2
(I1 and I2) are
is the sum of the moments at a certain cross section caused by all the transverse
loads,n is the number of the transverse loads,and the inertia moments of Zone 1 and Zone 2
(I1 and I2) are 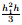 and
and 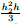 ,respectively. It can also be determined that which one,Zone 1 or Zone 2,is the tensile zone by the value of the stress component σx.
,respectively. It can also be determined that which one,Zone 1 or Zone 2,is the tensile zone by the value of the stress component σx.The stress components also satisfy the secondary boundary conditions at x = 0,shown as follows:
Equations (21a)-(21c) validate the correctness of the solving process of the stress component of the bi-modulus beam under the combined loads including concentrated and distributed force and moment.If the tensile modulus equals the compressive modulus,E1 = E2,the expressions of the stress components given by Eq. (20a) and Eq. (20b) are the same as the stress components stated by Timoshenko and Goodier[10] . Therefore,the correctness of the results derived above is verified.
The physical equation and the geometric equation in the plane stress condition are expressed by the known stress components,i.e.,
According to the displacement boundary conditions of the beam,the displacement components of the bi-modulus beam can be established by integrating the physical equation and the geometric equation.The elasticity analytical solution of the bi-modulus beam presented in this paper can be used for many statically determinate bi-modulus beams in engineering applications,such as the cantilever beam,the simply supported beam,the statically determinate continuous beam,and the statically determinate frame beam. The reaction forces of all the supports are calculated according to the static equilibrium conditions of the structure and the other external loads applied on the beam,as the combined loads applied on the bi-modulus beam. The analytic solution of the stress components in the tensile zone and the compressive zone can be calculated by the method in this paper,and then the displacement can also be obtained. If the end at x = l of the bi-modulus beam as shown in Fig. 1 is fixed,the beam becomes the cantilever beam. The stress components of the bi-modulus cantilever beam can be obtained by Eq. (20a) and Eq. (20b). If the end at x = l of the bi-modulus beam as shown in Fig. 1 is hinged,and P = − (al2/6 + bl/2) and M = 0 are defined,Eq. (20a) and Eq. (20b) also can express the stress components of the simply supported beam under the linearly distributed load. Therefore,Eq. (20a) and Eq. (20b) provide the general expressions and can be used for the bi-modulus beams with various loads and boundary conditions. 4 Example analysis and discussion 4.1 Error of same modulus solution
The error of results without the consideration of the difference between the tensile elastic modulus and the compressive modulus is studied by the example analysis. The comparison is conducted between the solution by the method stated in this paper and the same modulus elastic theory of the bi-modulus cantilever beam under the uniformly distributed load q.
A bi-modulus cantilever beam is 3h long,and the ratio of the tensile modulus to the compressive modulus is n = Ep/En. The stress distribution of the cross section at the fixed end is calculated according to Eq. (20a) and Eq. (20b) above. The error of the same modulus solution,δ1 ,is defined as the ratio of the difference between the same modulus solution and the bi-modulus solution with different n to the same modulus solution.
The stress component (σx) distributions on the cross section at the fixed end of the cantilever bi-modulus beam with the ratio of the tensile modulus to the compressive modulus n = 0.2, n = 1,and n = 5 are shown in Fig. 2,where the distance to the beam bottom is d. The following conclusions can be drawn from Fig. 2:
 |
| Fig. 2 Distribution of stress σx with n = 0.2,1,5 |
(i) The stress component distribution shapes are curved when n = 0.2 and n = 5. The stress component distribution shape is linear when n = 1.
(ii) The maximum tensile stress of the beam with n = 0.2 is 19.2q/b,which is 28.4% smaller than that of the beam (26.8q/b) with n = 1. The maximum compressive stress of the beam with n = 0.2 is -43.6q/b,whose absolute value is 62.7% larger than that of the beam with n = 1. The result is the opposite when n = 5. Therefore,for the cantilever bi-modulus beam with the ratio of the tensile modulus to the compressive modulus n = 0.2 and n = 5,the errors of the same modulus solution have been far more than the permitted amount 5% in engineering practice.
The δ1-n curves of the stress component σxat h (the top of the cross section),0.75 h,0.25 h, and 0 (the bottom of the cross section) are shown in Fig. 3. These curves express the error δ1 of the stress σxat different locations of the cross section using the same modulus solution varying with the ratio of the tensile modulus to the compressive modulus n. The following conclusions can be drawn from Fig. 3:
 |
| Fig. 3 δ1-n curves of stress σx at typical locations |
(i) δ1 of the maximum tensile stress,labeled as h,increases with the increase in n. The solution of the maximum tensile stress using the same modulus theory is smaller than the correct solution when n > 1 and larger than the correct solution when n < 1. The result of the maximum compressive stress,labeled as 0,is the opposite. The absolute value of δ1 exceeds 5% when n < 0.81 or n > 1.21. It means that the error of the maximum tensile and the compressive stress of the beam using the same modulus solution is non-negligible when n < 0.81 or n > 1.21.
(ii) δ1 of the stress at 0.75 h and 0.25 h increases first and then decreases as n increases. The solution of the stress at 0.75 h and 0.25 h using the same modulus theory is larger than the correct solution when n > 1 or n < 1. The curves are steep when n is less than about 0.7. It means that the error of the stress at 0.75 h and 0.25 h using the same modulus solution is sensitive to n when n is less than about 0.7.
The stress component (σy) distributions on the cross section at the fixed end of the cantilever bi-modulus beam with the ratio of the tensile modulus to the compressive modulus n = 0.2, n = 1,and n = 5 are shown in Fig. 4. It can be seen from Fig. 4 that the distribution curve of the stress σy decreases from q to 0 as the location from the top to the bottom. As for the same location on the cross section,the absolute value of the stress component σy is the largest when n = 5 and the smallest when n = 0.2.
 |
| Fig. 4 Distribution of stress σy with n = 0.2,1,5 |
The δ1-n curves of the stress component σyat 0.75 h,0.5 h,and 0.25 h are shown in Fig. 5. These curves express the error δ1 of σyat different locations of the cross section using the same modulus solution varying with n. The following conclusions can be drawn from Fig. 5:
 |
| Fig. 5 δ1-n curves of stress σy at typical locations |
(i) δ1 of the stress component σy at 0.75 h,0.5 h,and 0.25 h decreases with the increase in n. The solution of the stress component σy using the same modulus theory is smaller than the correct solution when n < 1 and larger than the correct solution when n > 1.
(ii) The curves are steep when n < 1. It means that the error of the stress component σyat 0.75 h,0.5 h,and 0.25 h using the same modulus solution is sensitive to n when n < 1. The curve labeled as 0.25 h is the steepest and is the most sensitive to n.
The stress component (τxy) distributions on the cross section at the fixed end of the cantilever bi-modulus beam with the ratio of the tensile modulus to the compressive modulus n = 0.2, n = 1,and n = 5 are shown in Fig. 6. The following conclusions can be drawn from Fig. 6:
 |
| Fig. 6 Distribution of stress τxy with n = 0.2,1,5 |
(i) The maximum shear stress values are the same when n = 0.2,n = 1,and n = 5,but occur at different locations on the cross section. The location of the maximum shear stress occurring is the closest to the bottom of the beam when n = 0.2.
(ii) As for n = 0.2,the distribution curve of the shear stress τxy is steep above the location the maximum shear stress occurs,and gentle below the location the maximum shear stress occurs. The result is the opposite when n = 5. The distribution curve is symmetric when n = 1.
The δ1-n curves of the shear stress τxy at 0.75 h,0.5 h,and 0.25 h are shown in Fig. 7. These curves express the error δ1 of the shear stress τxy at different locations of the cross section using the same modulus solution varying with n. The following conclusions can be drawn from Fig. 7:
 |
| Fig. 7 δ1-n curves of stress τxy at typical locations |
(i) δ1 of the shear stress τxy at 0.75 h increases as n increases. δ1 of the shear stress τxy at 0.25 h decreases as n increases. δ1 of the shear stress τxy at 0.5 h increases first and then decreases as n increases. The solution of the shear stress τxy at 0.75 h using the same modulus theory is smaller than the correct solution when n > 1,and the solution of the shear stress τxy at 0.25 h using the same modulus theory is larger than the correct solution when n > 1. The solution of the shear stress τxy at 0.5 h using the same modulus theory is smaller than the correct solution whether n > 1 or n < 1. The absolute value of δ1 of the maximum shear stress τxy exceeds 5% when n < 0.19 or n > 3.31. It means that the error of the maximum shear stress of the beam using the same modulus solution is non-negligible when n < 0.19 or n > 3.31.
(ii) The three curves are steep when n < 1 and gentle when n > 1. It means that the error of the shear stress at 0.75 h,0.5 h,and 0.25 h using the same modulus solution is sensitive to n when n < 1. 4.2 Error of material mechanics solution
The material mechanics solution was derived based on the assumptions of the plane-section and σy = 0 in Ref. [6]. The shear stresses τxy of the two solutions are the same. The stress components σxof the two solutions are discussed herein.
The error of the material mechanics solution is studied by the example analysis. The comparison is conducted between the elastic mechanics solution by the method stated in this paper and the material mechanics solution of the bi-modulus cantilever beam. The error of the material mechanics,δ2,is defined as the ratio of the difference between the material mechanics solution and the elastic mechanics solution to the material mechanics solution. The effects of the distributed load pattern and the span-to-height ratio on the error δ2 of the maximum tensile stress and the maximum compressive stress are studied.
Figure 8 shows the δ2-n curves of the maximum tensile stress of the bi-modulus beam with different span-to-height ratios L/h=2,3 under the uniformly distributed load q(x) = q and the linearly distributed load q(x) = qx/l. The maximum compressive stress is shown in Fig. 9. It can be seen from Fig. 8 and Fig. 9 that
 |
| Fig. 8 δ2-n curves of maximum tensile stress |
 |
| Fig. 9 δ2-n curves of maximum compressive stress |
(i) δ2 of the maximum tensile stress increases with the increase in n. The solution of the maximum tensile stress using the material mechanics solution is smaller than the correct solution when n > 6.6. δ2 of the maximum compressive stress decreases with the increase in n. As for the maximum compressive stress,the material mechanics solution is smaller than the correct solution when n < 0.15 for the beam under the uniformly distributed load. The material mechanics solution is always larger than the correct solution for the beam under the linearly distributed load.
(ii) The three curves are steep when n < 1 and gentle when n > 1. It means that the error of the maximum tensile stress and the maximum compressive stress using the material mechanics solution is sensitive to n when n < 1.
(iii) The error δ2 of the maximum tensile stress and the maximum compressive stress using the material mechanics solution decreases as the span-to-height ratio increases. The error δ2 is proportional to the inverse square of the span-to-height ratio. The error δ2 is apparent when L/h ≤ 5,which means that the analytical solution obtained in this paper is precise compared with the material mechanics solution in Ref. [6] only when L/h ≤ 5.
(iv) The error δ2 of the maximum tensile stress and the maximum compressive stress of the beam under the uniformly distributed load is smaller than that of the linearly distributed load. The error δ2 of the maximum compressive stress of the beam under the linearly distributed load is up to 7.5% when n = 1 and increases rapidly with n. Therefore,the error is non-negligible when the beam is under the increasing distributed load from the free end to the fixed end, which limits the material mechanics solution to be used in the bi-modulus beam when L/h ≤ 5.
| [1] | Ye, Z. M., Chen, T., and Yao, W. J. Progress of theory and finite element method on different modulus elasticity. Mechanics in Engineering, 26(2), 9-14 (2004) |
| [2] | Bert, C. W. Models for fibrous composites with different properties in tension and compression. Journal of Engineering Materials and Technology, 99(4), 344-349 (1977) |
| [3] | Bruno, D., Lato, S., and Sacco, E. Nonlinear analysis of bimodular composite plates under com-pression. Computational Mechanics, 14(1), 28-37 (1994) |
| [4] | Ambartsumyan, S. A. Elasticity Theory of Different Moduli (Trans. by Wu, R. F. and Zhang, Y. Z.), China Railway Publishing House, Beijing (1986) |
| [5] | Ye, Z. M., Yu, H. R., and Yao, W. J. A new elasticity and finite element formulation for different Young's modulus when tension and compression loading. Journal of Shanghai University (English Edition), 5(2), 89-92 (2001) |
| [6] | Yao, W. J. and Ye, Z. M. Analytical solution for bending beam subject to lateral force with different modulus. Applied Mathematics and Mechanics (English Edition), 25(10), 1107-1117 (2004) DOI 10.1007/BF02439863 |
| [7] | He, X. T., Chen, S. L., and Sun, J. Y. Elasticity solution of simple beams with different modulus under uniformly distributed load. Engineering Mechanics, 24(10), 51-56 (2007) |
| [8] | Wu, X., Huang, C., and Sun, J. Kantorovich solution of bimodulus cantilever beam under dis-tributed loads. Journal of Hunan University of Science and Technology, 27(2), 55-59 (2012) |
| [9] | Yang, Q., Zheng, B. L., Zhang, K., and Zhu, J. X. Elastic solutions of a functionally graded cantilever beam with different modulus in tension and compression under bending loads. Applied Mathematical Modelling, 27(2), 1403-1416 (2014) |
| [10] | Timoshenko, S. P. and Goodier, J. N. Theory of Elasticity, 3rd ed., McGraw-Hill, New York (1970) |
 2015, Vol. 36
2015, Vol. 36



























