2015, Vol. 36
Shanghai University
Article Information
- M. H. YAS, N. MOLOUDI. 2015.
- Three-dimensional free vibration analysis of multi-directional functionally graded piezoelectric annular plates on elastic foundations via state space based differential quadrature method
- J. Meteor. Res., 36(4): 439-464
- http://dx.doi.org/10.1007/s10483-015-1923-9
Article History
- Received 2014-04-27;
- in final form 2014-10-02
a,outer radius of anuular plate;
b,inner radius of anuular plate;
h,thickness of anuular plate;
kw,Winkler stiffness of elastic foundation;
kg,shear stiffness of elastic foundation;
σr,σθ,σz,axial stress components;
τrθ,τθz,τrz,shear stress components;
ur,uθ,uz,mechanical displacement components;
Dr,Dθ,DZ,electrical displacement components;
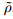,material density;t,time;
∈r,∈θ,∈z,strain components;
γθz,γrθ,γrz,strain components;
Er,Eθ,Ez,electric field components;
ψ,electric potential. 1 Introduction
Piezoelectric materials have been widely used in electromechanical systems and structures in application of sensors and actuators[1, 2, 3]. However,there are some weaknesses in the traditional laminated smart devices. For example,they may crack at low temperature or peel at high temperature,which will reduce the lifetime and reliability of these piezoelectric devices[4]. In order to improve mechanical and electrical properties at layer interfaces,functionally graded piezoelectric materials (FGPMs) with material properties varying smoothly and continuously along one (or more) direction(s) have been developed to enhance the lifetime and reliability of advanced piezoelectric structures[5, 6, 7, 8]. For optimal design and fabrication of an FGPM with desired properties,it is necessary to thoroughly understand the static and dynamic behaviors of FGPM structures in complex environments. Lee and Jiang[9] studied the static behavior of a simply supported piezoelectric plate using the state space method (SSM). Bert and Malik[10] advanced a new numerical method named the differential quadrature method (DQM) for analysis of laminated composite structures. To examine the bending and free vibration of transversely isotropic FGPM plates,Chen and Ding[11, 12] established a new state space model. Lim and He[13] obtained an exact solution of a compositionally graded piezoelectric layer under uniform stretch,bending,and twisting in Saint Venant sense. Reddy and Cheng[14] studied a threedimensional solution of smart functionally graded plate. Zhong and Shang[7] were the first to present a three-dimensional exact analysis of simply supported FGPM rectangular plates via the SSM when the material constants vary exponentially along the thickness of the plate. Via the SSM,Lu et al.[8, 15] derived the exact solutions of a simply supported FGPM plate/laminate under cylindrical bending by Stroh-like formalism. Li et al.[16] presented a three-dimensional analytical solution for a transversely isotropic functionally graded piezoelectric (FGP) circular plate subjected to a uniform electric potential difference using the direct displacement method. Xiang and Shi[17] investigated static analysis of FGP actuators or sensors under a combined electro-thermal load using the airy stress function method. Li and Shi[18] investigated free vibration of an FGP beam via the state space based differential quadrature method (SSDQM). Using the DQM and the state space approach,Alibeigloo and Nouri[19] studied the three-dimensional solution for static analysis of functionally graded cylindrical shell with bonded piezoelectric layers. Jam and Nia[20] presented a semi-analytical solution for free vibration of FGP annular plate with different boundary conditions based on the three-dimensional theory of elasticity. In the above mentioned papers,the material properties are assumed to have a smooth variation usually in the thickness direction only. However,there are practical occasions which require the materials graded in two or three directions. Thus,it is necessary to develop appropriate methods to investigate the mechanical responses of multi-directional functionally graded structures[21]. Using the meshless local Petrov-Galerkin (MLPG),Qian and Batra[22] investigated static,free, and forced vibration of a cantilever beam whose material properties are power-law functions of the two coordinates. Using the MLPG method,Qian and Ching[23] derived optimal natural frequencies of two-dimensiona FGPM plates with a two-way Mori-Tanaka scheme. L¨u et al.[24] used a semi-analytical approach named the SSDQM to present the three-dimensional elasticity solution analysis of multi-directional functionally graded plates. Nie and Zhong[21] investigated dynamic analysis of multi-directional functionally graded annular plates using the SSDQM. Plates resting on elastic foundations with different shape and boundary conditions have wide application in mechanical,civil,aerospace,and nuclear engineering fields. Hence,dynamical analysis of plates resting on elastic foundation is important in studying the influence of the elastic foundation on the dynamic behavior of plates. There are many researchers who used plates on the elastic foundation to study free vibration[25, 26, 27, 28]. Limited studies have been done which concerned with free vibration of functionally graded plates on the elastic foundation. Using the DQM,Malekzadeh[29] studied three-dimensional free vibration of thick functionally graded plates on elastic foundations. Amini et al.[30] described a method for the three-dimensional free vibration analysis of rectangular FGM plates resting on an elastic foundation using the Chebyshev polynomials and the Ritz method. Using the DQM,Hosseini-Hashemi et al.[31, 32] studied buckling and free vibration behaviors of radially functionally graded circular and annular sector thin plates for constant and variable thickness based on the classical plate theory. Yas and Tahouneh[33] presented three-dimensional free vibration analysis of thick functionally graded annular plate on the elastic foundation via the DQM. Y as et al.[34] used the SSDQM to make three-dimensional free vibration analysis of FGP annular plate on elastic foundations. To the authors’ knowledge,three-dimensional free vibration analysis of multi-directional FGP annular plates on elastic foundations has not been implemented before. Besides application of the state space approach combined with the DQM,the analysis of the multi-directional FGP annular plates on elastic foundations has not been reported in the literature. For this purpose, this paper deals with three-dimensional free vibrations of multi-directional FGP annular plates resting on elastic foundation under different boundary conditions including simply supportedsimply supported (s-s),simply supported-clamped (s-c),and clamped-clamped (c-c) ends. The material properties are assumed to vary continuously along radial and thickness directions and have exponent-law distribution. A semi-analytical approach named the SSDQM[35, 36, 37, 38] is adopted which can give an analytical solution along the thickness using the SSM[39, 40] and an approximate solution along the radial direction using the one-dimensional DQM[41, 42, 43, 44, 45]. The convergency and accuracy of the present method are demonstrated through numerical results. The influence of material property graded variations and the circumferential wave number on the dynamic behavior is also investigated. 2 Basic equations 2.1 Governing equations
Consider a multi-directional orthotropic FGP annular plate of the inner radius b,the outer radius a,and the thickness h resting on two parameter elastic foundations,as depicted in Fig. 1. The Pasternak model with Winkler stiffness of Kw and shear stiffness of Kg is used to describe the interaction between the elastic foundation and the annular plate. A cylindrical coordinate system (r,θ,z ) with the origin on the center of the bottom plane is used. The equations of motion and Gauss law of electrostatics,in the absence of the body forces and electric charge density,are
where σr,σθ,and σz are the axial stress components,τrθ,τθz,and τrz are the shear stress components,ur,uθ,uz are the mechanical displacement components,Dr,Dθ and Dz are the electrical displacement components,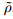
denotes the material density,and t is the time.
 |
| Fig. 1 Geometry of FGPM annular plate on elastic foundation |
The strain-displacement and the electric field-potential relations are
where ∈r,∈θ,∈z,γθz,γrθ,and γrz are the strain components,Er,Eθ,and Ez are the electric field components,and ψ is the electric potential.
For an orthotropic FGPM,the constitutive equations are
where σ = [σr ,σθ,σz,τrθ,τθz,τrz]T,E = [Er,Eθ,Ez],∈ = [∈r,∈θ,∈z,γθz,γrθ,γrz],D = [Dr,Dθ,DZ]T,and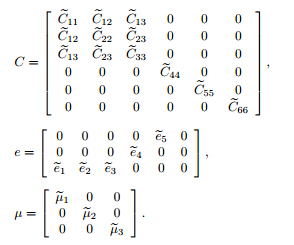
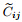are the material elastic stiffness coefficients,
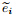are the
piezoelectric stiffness coefficients,and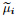 
are the dielectric permittivity coefficients.
For the multi-directional FGPMs,the material properties are assumed to be continuous functions of the coordinates and have the following exponent-law distributions along the thickness and radial directions of the plate:
where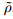
can be 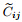,,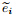,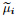and 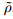,p is the corresponding value of 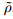at the center of the bottom
plane,and λ1 and λ2 denote the material property graded indexes in the thickness and radial
directions,respectively. They can be determined by the value of material properties at the
center point of the bottom plane and the outer edge of the top plane,i.e.,[21]
2.2 Boundary conditions
In this paper,three different kinds of end boundary conditions are considered: c-c,s-c,and s-s ends.
The mechanical and electrical boundary conditions are
The electrical and mechanical boundary conditions at the bottom and top surfaces of the plate can be expressed as where
Deriving an analytical solution for problems with multi-directional non-homogeneity is more difficult. Thus,recently,researchers have used a new method called the SSDQM to solve this kind of problems. The SSDQM is a semi-analytical method which is a combination of an analytical method (the SSM) and an approximate method (the DQM). The SSDQM uses the SSM to get the analytical solution in the thickness direction of the annular plate and uses the one-dimensional DQM to obtain the approximate solution in the radial direction of the annular plate.
When the annular plate vibrates with the natural frequency,it is possible to separate the dependence of time and the circumferential coordinate for certain types of vibration using the assumed mechanical displacements field in the following form[46] :
The stress is assumed in the following form: where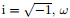
is the natural frequency,and m = 0,1,2,···,∞ is the circumferential wave
number. In the above equations,m = 0 means the axisymmetric vibration. To obtain another
set of free vibration modes,m should be interchanged.
For simplicity and generality,the following non-dimensional parameters are introduced:
where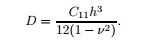
The DQM is an accurate numerical method to solve the initial and boundary problems and requires minimum computational efforts. The principle of the DQM is that the nth order partial derivative of a continuous function ƒ(r,z) with respect to r at a given point rican be expressed by the linear sum of weighted function ƒ(r,z) values at all of the discrete points in the domain of,i.e.,
where N is the number of sampled points at r domain,and gij(n) are the weighting coefficients which only depend on grid spacing[35, 47]. 3.2 Dispersion of state space equations
Let the mechanical displacements ur,uθ ,and uz,the electrical displacement Dz,the stresses σz,τrz,and τθz,and the electric potential ψ be the state variables. By combining Eqs. (1)-(4), using Eqs. (11)-(13),and applying the DQM expressed in Eq. (14),the following state space equations at an arbitrary sampling point ri are then obtained:
where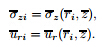
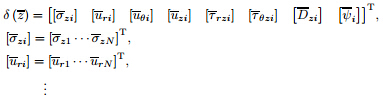
The solution to Eq. (24) can be written as
where exp(Mb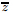
) is the matrix exponential function,and δb (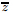) and δb (0) are the values of the
state variables at an arbitrary plane 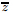and the bottom plane 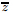= 0,respectively. In order
to obtain the relationship between the state variables of the top and bottom of the plate,
substituting 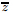= 0 into Eq. (25),we can obtain
where T = exp(Mb).
Then,Eq. (26) can be expressed in a sub-matrix of
By applying the DQM on Eq. (10),the effect of elastic foundations at the bottom of the plate can be obtained as K is given in Appendix C.
By substituting the boundary conditions of the bottom and top surfaces of the plate,the following equations can be found:
To find the nontrivial solution to Eq. (29),it is required that the determinant of the coefficient matrix equals zero,which yields the natural frequency of the plate. Note that the numerical instability is apt to occur for the global analysis according to Eq. (25) when the plate is strongly thick or when the discrete point number is very large. This is mainly due to the fast increasing eigenvalues of the coefficient matrix Mb in Eq. (24) as the thickness ratio or the discrete point number increases[24]. 4 Results and discussion
For numerical computation,sampling points with the following coordinates are used[47]:
where a is the outer radius,b is the inner radius,and N is the number of sampling points in the r-direction. 4.1 Validation
Since the free vibration analysis of the multi-directional FGPM on the elastic foundation has not been studied before and there is no reference in the literature to validate the obtained results,a kind of validation is done by applying some simplification to the governing equations in order to gain simple cases of the present problem. By eliminating electrical terms from governing equations,we can get the natural frequency of multi-directional orthotropic FGPM annular plate. The material constants for the FGPM plate at the center of the bottom plate are
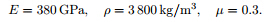
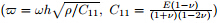of annular plate for different numbers of sampling point
N in the radial direction. The same problem has been studied by Nie and Zhong[21].
 |
The comparison of the first three non-dimensional natural frequency parameters for the conventional thickness-wise uni-directional FGPM (λ1 = 1 and λ2 = 0),the uni-directional FGPM having continues distribution along the radial direction (λ1 = 0 and λ2 = 1),and the bi-directional FGPM having continuous distribution along both the radial and thickness directions (λ1 = 1 and λ2 = 1) between the present results and the results from Nie and Zhong[21] are shown in Table 1. There is good agreement between the results.
The material properties at the center of the bottom surface of orthotropic FGPM annular plate are given in Table 2.
 |
By setting λ2 = 0,the convergence results of the first three non-dimensional frequency
parameters 
of a conventional thickness-wise uni-directional FGPM annular
plate with the c-c end boundary condition (a = 1.0 m,b = 0.2 m,h = 0.1 m,and k
g = Kw = 0)
for different numbers of sampling point N and different material graded indexes in the thickness
direction λ1
are shown in Table 3. The results are presented together with those reported by
Jam and Nia[20]
,and again it can be observed that there is good agreement between them.
 |
In Table 4,the comparison results of the second non-dimensional natural frequency parameters 
for the thickness-wise uni-directional FGPM annular plate
on elastic foundations (a = 1.0 m,b = 0.2 m, Kg = 100,and λ2 = 0) with different boundary conditions including simply supported at the inner radius,clamped at the outer radius,c-c
between the present solution,and those reported by Yas et al.[34]
are shown. As observed,there is good agreement between the results.
 |
According to Eq. (5),it is assumed that the sum of bi-directional graded indexes is constant
(λ1 + λ2 = const.). In Tables 5-9,the effects of different variations of material properties
in the interior of the bi-directional FGPM annular plate and elastic foundation coefficients
on the first three non-dimensional natural frequency parameters 
of the bidirectional FGPM plate (b = 0.2 m and a = 1.0 m) are shown for different plate thicknesses
(h = 0.01 m,0.05 m,0.1 m,and 0.2 m) and various boundary conditions including c-c and
simply supported at the inner radius and clamped at the outer radius,respectively.
 |
 |
 |
 |
 |
It can be noticed that the first three non-dimensional natural frequency parameters increase with the increase in the ratio of the radial graded index (λ2 / λ1) and the graded thickness,i.e., the sum of bi-directional graded indexes,which is constant (λ1 + λ2 = const.).
It results that the radial graded variation has more effect on the improvement of the stiffness of the plate. Also,one can see that the Winkler and shearing layer elastic coefficient have significant effects on the non-dimensional natural frequency parameters. As observed,the effect of the Winkler and shearing layer elastic coefficient increase with the increases in the ratio of the radial graded index and the graded thickness index (λ2 / λ1) . It is observed that the non-dimensional natural frequency parameters decrease with the increase in the thickness and change of the support type from c-c to s-c.
Figures 2-4 and 5-7 show the effect of the shearing layer elastic coefficient on the first three non-dimensional natural frequency parameters at a constant value of the Winkler elastic coefficient (Kw = 100) and different ratios of the radial graded index and the graded thickness index (λ2 / λ1) ,i.e.,the sum of bi-directional graded indexes,which is constant (λ1 + λ2 = const.).
 |
| Fig. 2 Variations of first non-dimensional natural frequency parameter of c-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kw = 100) |
 |
| Fig. 3 Variations of second non-dimensional natural frequency parameter of c-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kw = 100) |
 |
| Fig. 4 Variations of third non-dimensional natural frequency parameter of c-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kw = 100) |
 |
| Fig. 5 Variations of first non-dimensional natural frequency parameter of s-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kw = 100) |
 |
| Fig. 6 Variations of second non-dimensional natural frequency parameter of s-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kw = 100) |
 |
| Fig. 7 Variations of third non-dimensional natural frequency parameter of s-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kw = 100) |
The figures are drawn for different boundary conditions including c-c and s-c,respectively. The first three non-dimensional natural frequency parameters increase with the increase in the shearing layer elastic coefficient,the ratios of the radial graded index,and the graded thickness index (λ2 / λ1 ) . Also,it can be seen that the most effective range of shearing layer elastic coefficient on the non-dimensional natural frequency parameters deceases with the increase in the ratio of the radial graded index and the graded thickness index (λ2 / λ1) . For example, the most effective range of the shearing layer elastic coefficient on the non-dimensional natural frequency parameters for λ2 / λ1 = 0 is from 102 to 106,and the range for λ2 / λ1 = 7 is from 102 to 103.
Figures 8-10 and 11-13 show the effect of the Winkler elastic coefficient on the first three non-dimensional natural frequency parameters at a constant value of shearing layer elastic coefficient (Kg = 100) and different ratios of the graded indexes (λ2 / λ1),i,e.,the sum of bi-directional graded indexes,which is constant (λ2 / λ1 = const.).
 |
| Fig. 8 Variations of first non-dimensional natural frequency parameter of c-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kg = 100) |
 |
| Fig. 9 Variations of second non-dimensional natural frequency parameter of c-c multi-directional FGP plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m and Kg = 100) |
 |
| Fig. 10 Variations of third non-dimensional natural frequency parameter of c-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kg = 100) |
 |
| Fig. 11 Variations of first non-dimensional natural frequency parameter of s-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kg = 100) |
 |
| Fig. 12 Variations of second non-dimensional natural frequency parameter of s-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kg = 100) |
 |
| Fig. 13 Variations of third non-dimensional natural frequency parameter of s-c multi-directional FGPM plates on elastic foundation vs. shearing layer elastic coefficient for different ratios of graded indexes (λ2 / λ1) (b = 0.2 m,a = 1 m,h = 0.1 m,and Kg = 100) |
The first three non-dimensional natural frequency parameters increase with the increase in the Winkler elastic coefficient and the ratio of the graded indexes (λ2 / λ1 ) . Also,it can be seen that the most effective range of the Winkler elastic coefficient on the non-dimensional natural frequency parameters changes with the variation of the ratio of graded indexes (λ2 / λ1). With the increase in the ratio of graded indexes (λ2 / λ1),the most effective range of the Winkler elastic coefficient changes from higher values to lower values. For example,the most effective range of the Winkler elastic coefficient on the non-dimensional natural frequency parameters for λ2 / λ1 = 0 is from 104 to 107,and the range for λ2 / λ1 = 7 is from 102 to 105. It can be seen that by increasing the shearing layer elastic coefficient in comparison to increasing the Winkler elastic coefficient,the first three non-dimensional natural frequency parameters increase faster. 5 Conclusions
The three-dimensional free vibration analysis of multi-directional FGP annular plates resting on elastic foundations with various boundary conditions using the semi-analytical approach named the SSDQM is presented. The effects of variation of the ratio of the radial graded index to the graded thickness index (λ2 / λ1 ),the Winkler and shearing layer elastic coefficients,the thickness of annular plate,and the circumferential wave number on the non-dimensional natural frequency of annular plate are also studied. This paper shows
(i) The convergence speed and accuracy of the present method through obtained numerical results.
(ii) Good agreement with the existing numerical results in the literature.
(iii) The non-dimensional natural frequency parameters increase with the increase in the ratio of the radial graded index and the graded thickness index.
(iv) It results that the radial graded variation has more effect on the improvement of the stiffness of the plate.
(v) The Winkler and shearing layer elastic foundation have significant influence on the non-dimensional natural frequency parameters of FGPM annular plate. The non-dimensional natural frequency parameters reduce by increasing the thickness of the plate and by changing the support type from c-c to s-c.
(vi) The Winkler and shearing layer elastic coefficients are much more effective at higher values of the ratio of graded indexes on non-dimensional natural frequency parameters of multidirectional FGPM annular plates. Appendix A
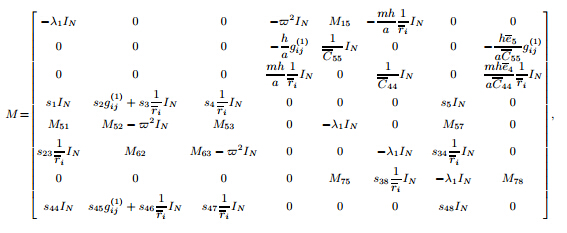
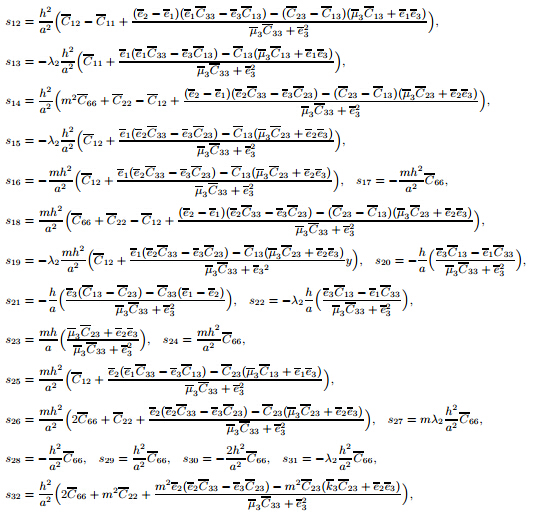
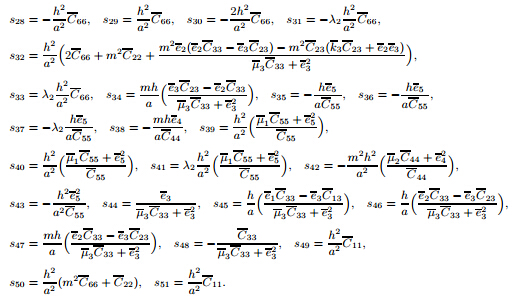
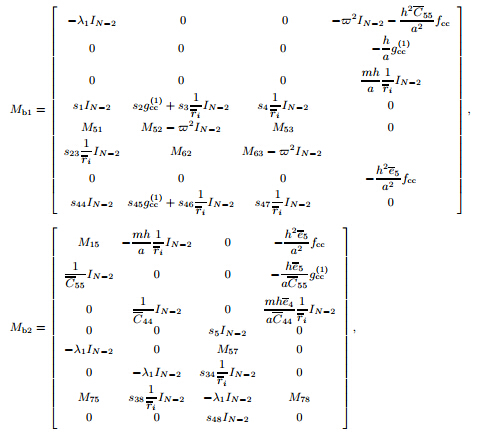
(c-c): Mb = [Mb1 Mb2],where
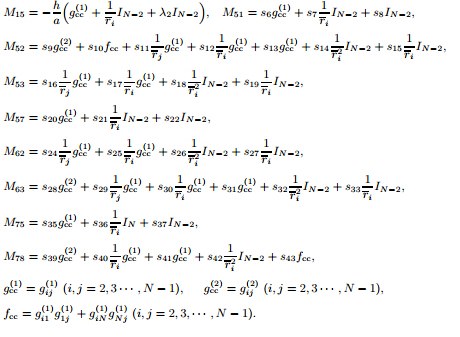
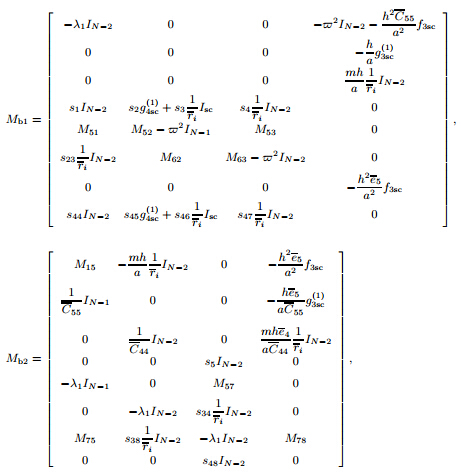
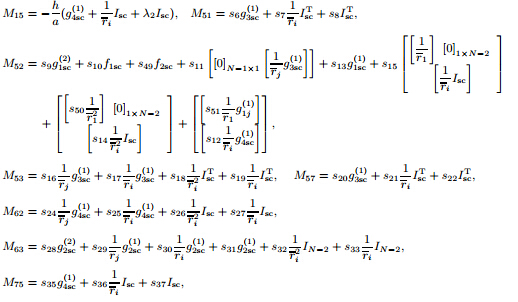
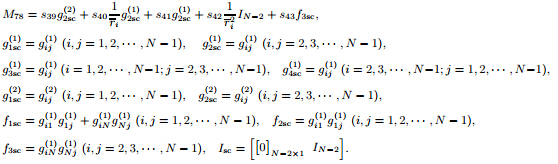
Assumption 1
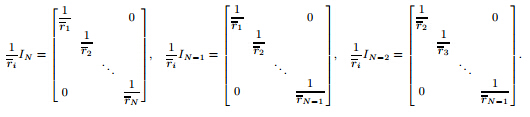
Assumption 2
If f = fij (i = n,··· ,n′,j = m,···,m′) ,then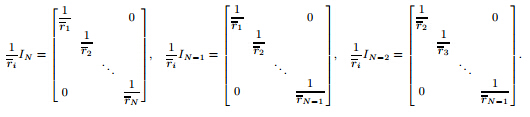
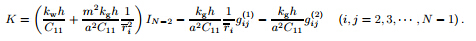
| [1] | Gandhi, M. V. and Thompson, B. S. Smart Materials and Structures, Chapman and Hall, London (1992) |
| [2] | Rao, S. S. and Sunar, M. Piezoelectricity and its use in disturbance sensing and control of flexible structures. Applied Mechanics Reviews, 47(4), 113-123 (1994) |
| [3] | Branco, P. J. and Dente, J. A. On the electromechanics of a piezoelectric transducer using a bimorph cantilever undergoing asymmetric sensing and actuation. Smart Materials and Structures, 13(4), 631-642 (2004) |
| [4] | Kruusing, A. Analysis and optimization of loaded cantilever beam microactuators. Smart Materials and Structures, 9(2), 186-196 (2000) |
| [5] | Zhu, X. H. and Meng, Z. Y. Operational principle fabrication and displacement characteristic of a functionally gradient piezoelectric ceramic actuature. Sensors and Actuators, 48(3), 169-176 (1995) |
| [6] | Wu, C. C., Kahn, M., and Moy, W. Piezoelectric ceramics with functional gradients: a new application in material design. Journal of the American Ceramic Society, 79(3), 809-812 (1996) |
| [7] | Zhong, Z. and Shang, R. T. Three-dimensional exact analysis of simply supported functionally gradiant piezoelectric plate. International Journal of Solids and Structures, 40(20), 5335-5352 (2003) |
| [8] | Lu, P., Lee, H. P., and Lu, C. Exact solutions for simply supported functionally graded piezoelectric laminates by Stroh-like formalism. Composite Structures, 72(3), 352-363 (2006) |
| [9] | Lee, J. S. and Jiang, L. Z. Exact electroelastic analysis of piezoelectric laminae via state-space approach. International Journal of Solids and Structures, 33(7), 977-990 (1996) |
| [10] | Bert, C. W. and Malik, M. Differential quadrature: a powerful new technique for analysis of composite structures. Composite Structures, 39(3-4), 179-189 (1997) |
| [11] | Chen, W. Q. and Ding, H. J. Bending of functionally graded piezoelectric rectangular plates. Acta Mechanica Solida Sinica, 13(4), 312-319 (2000) |
| [12] | Chen, W. Q. and Ding, H. J. On free vibration of a functionally graded piezoelectric rectangular plate. Acta Mechanica, 153(3-4), 207-216 (2002) |
| [13] | Lim, C. W. and He, L. H. Exact solution of a compositionally graded piezoelectric layer under uniform stretch bending and twisting. International Journal of Mechanical Sciences, 43(11), 2479- 2492 (2001) |
| [14] | Reddy, J. N. and Cheng, Z. Q. Three-dimensional solutions of smart functionally graded plates. Journal of Applied Mechanics, 68(2), 234-241 (2001) |
| [15] | Lu, P., Lee, H. P., and Lu, C. An exact solution for simply supported functionally graded piezoelectric laminates in cylindrical bending. International Journal of Mechanical Sciences, 47(3), 437-458 (2005) |
| [16] | Li, X. Y., Ding, H. J., and Chen, W. Q. Three-dimensional analytical solution for a transversely isotropic functionally graded piezoelectric circular plate subject to a uniform electric potential difference. Science in China Series G: Physics, Mechanics and Astronomy, 51(8), 1116-1125 (2008) |
| [17] | Xiang, H. J. and Shi, Z. F. Static analysis for functinoally graded piezoelectric actuators or sinsors under a combined electro-thermnl load. European Journal of Mechanics-A/Solids, 28(2), 338-346 (2009) |
| [18] | Li, Y. and Shi, Z. F. Free vibration of functionally graded piezoelectric beam via state-space based differential quadrature. Composite Structures, 87(3), 257-264 (2009) |
| [19] | Alibeigloo, A. and Nouri, V. Static analysis of functionally graded cylindrical shell with piezoelectric layers using differential quadrature method. Composite Structures, 92(8), 1775-1785 (2010) |
| [20] | Jam, J. E. and Nia, N. G. Semi-analytical solution for 3-D vibration of FGPM annular plates. International Journal of Emerging Trends in Engineering and Development, 3, 149-166 (2011) |
| [21] | Nie, G. J. and Zhong, Z. Dynamic analysis of multi-directional functionally graded annular plates. Applied Mathematical Modelling, 34(3), 608-616 (2010) |
| [22] | Qian, L. F. and Batra, R. C. Design of bidirectional funcaionally graded plate for optimal natural frequencies. Journal of Sound and Vibration, 280(1-2), 415-424 (2005) |
| [23] | Qian, L. F. and Ching, H. K. Static and dynamic analysis of 2-D functionally graded elasticity by using meshless local Petrov-Galerkin method. Journal of the Chinese Institute of Engineers, 27(4), 491-503 (2004) |
| [24] | Lü, C. F., Lim, C. W., and Chen, W. Q. Semi-analytical analysis for multi-directional functionally graded plates: 3-D elasticity solutions. International Journal for Numerical Methods in Engineering, 79(1), 25-44 (2009) |
| [25] | Gupta, U. S., Ansari, A. H., and Sharma, S. Buckling and vibration of polar orthotropic circular plate resting on Winkler foundation. Journal of Sound and Vibration, 297(3-5), 457-476 (2006) |
| [26] | Hosseini-Hashemi, S., Rokni Damavandi Taher, H., and Omidi, M. 3-D free vibration analysis of annular plates on Pasternak elastic foundation via p-Rite method. Journal of Sound and Vibration, 311(3-5), 1114-1140 (2008) |
| [27] | Hosseini-Hashemi, S., Omidi, M., and Rokni Damavandi Taher, H. The validity range of CPT and Mindlin plate theory in comparison with 3-D vibrational analysis of circular plateson the elastic foundation. European Journal of Mechanics-A/Solids, 28(2), 289-304 (2009) |
| [28] | Malekzadeh, P., Afsari, A., Zahedinejad, P., and Bahadori, R. Three-dimensional layerwise-finite element free vibrition analysis of thick laminated annular plates on elastic foundation. Applied Mathematical Modelling, 34(3), 776-790 (2010) |
| [29] | Malekzadeh, P. Three-dimensional free vibration analysis of thick functionally graded plates on elastic foundations. Composite Structures, 89(3), 367-373 (2009) |
| [30] | Amini, M. H., Soleimani, M., and Rastgoo, A. Three-dimensional free vibration analysis of functionally graded material plates resting on an elastic foundataon. Smart Materials and Structures, 18(8), 085015 (2009) |
| [31] | Hosseini-Hashemi, S., Akhavan, H., Rokni Damavandi Taher, H., Daemi, N., and Alibeigloo, A. Differential quadrature analysis of functionally grared circular and annular sector plates on elastic foundation. Materials and Design, 31(4), 1871-1880 (2010) |
| [32] | Hosseini-Hashemi, S., Rokni Damavandi Taher, H., and Akhavan, H. Vibration analysis of radially FGM sectorial plates of variable thickness on elastic foundations. Composite Structures, 92(7), 1734-1743 (2010) |
| [33] | Yas, M. H. and Tahouneh, V. 3-D free vibration analysis of thick functionally graded annular platrs on Pasternak elastic foundation via differential quadrature method (DQM). Acta Mechanica, 223(9), 43-62 (2012) |
| [34] | Yas, M. H., Jodaei, A., Irandoust, S., and Nasiri-Aghhdam, M. Three-dimensional free vibration of functionally graded piezoelectric annular plates on elastic foundations. Meccanica, 47(6), 1401- 1423 (2012) |
| [35] | Chen, W. Q., Lv, C. F., and Bian, Z. G. Elasticity solution for free vibration of laminated beams. Composite Structures, 62(1), 75-82 (2003) |
| [36] | Chen, W. Q., Lv, C. F., and Bian, Z. G. Free vibration of generally laminated beams via statespace based differential quadrature. Composite Structures, 63(3-4), 417-425 (2004) |
| [37] | Chen, W. Q. and Lü, C. F. 3D free vibration analysis of cross-ply laminated plates with one pair of opposite edges simply supported. Composite Structures, 69(1), 77-87 (2005) |
| [38] | Lü, C. F., Chen, W. Q., Xu, R. Q., and Lim, C. W. Semi-analytical elasticity solutions for bi-directional functionally graded beams. International Journal of Solids and Structures, 45(1), 258-275 (2008) |
| [39] | Lee, J. S. and Jiang, L. Z. Exact electroelastic analysis of piezoelectric laminae via state space approach. International Journal of Solids and Structures, 33(7), 977-990 (1996) |
| [40] | Zhong, Z. and Shang, E. T. Three-dimensional exact analysis of a simply supported functionally graded piezoelectric plate. International Journal of Solids and Structures, 40(20), 5335-5352 (2003) |
| [41] | Bert, C. W. and Malik, M. The differential quadrature method in computational mechanics. Applied Mechanics Reviews, 49(1), 1-28 (1996) |
| [42] | Karami, G. and Malekzadeh, P. A new differential quadrature methodology for beam analysis and the associated differential quadrature element method. Computer Methods in Applied Mechanics and Engineering, 191(32), 3509-3526 (2002) |
| [43] | Malekzadeh, P. Differential quadrature large amplitude free vibration analysis of laminated skew plates based on FSDT. Composite Structures, 83(2), 189-200 (2008) |
| [44] | Malekzadeh, P., Setoodeh, A. R., and Barmshouri, E. A hybrid layerwise and differential quadrature method for in-plane free vibration of laminated thick circular arches. Journal of Sound and Vibration, 315(1-2), 215-225 (2008) |
| [45] | Wang, X. W. and Wang, Y. L. Free vibration analyses of thin sector plates by the new version of differential quadrature method. Computer Methods in Applied Mechanics and Engineering, 193(36-38), 3957-3971 (2004) |
| [46] | Nie, G. J. and Zhong, Z. Semi-analytical solution for three-dimensional vibration of functionally graded circular plates. Computer Methods in Applied Mechanics and Engineering, 196(49-52), 4901-4910 (2007) |
| [47] | Shu, C. and Richards, B. E. Application of generalized differential quadrature to solve twodimensional incompressible Navier-Stokes equations. International Journal for Numerical Methods in Fluid, 15, 791-798 (2012) |