Shanghai University
Article Information
- Xiaofan GOU, Jian QIN. 2015.
- Analytic calculation of magnetic force between two current-carrying coils
- J. Meteor. Res., 36(4): 475-486
- http://dx.doi.org/10.1007/s10483-015-1924-9
Article History
- Received 2014-05-09;
- in final form 2014-08-07
Current-carrying coils are basic elements for constructing electromagnetic magnet systems such as linear actuators and motors[1, 2],or even higher field magnets from high temperature superconductor wires or tapes[3, 4, 5],for example,the magnetic resonance imaging (MRI)[6] or nuclear magnetic resonance (NMR)[7] magnet,and the international thermonuclear experimental reactor (ITER) magnet system[8, 9, 10]. For the design and safety operation[11] of these magnet systems with current-carrying coils,it is important to accurately calculate the magnetic field of a current-carrying coil and the magnetic force between two coils.
So far,some important studies have been accomplished on calculating of the magnetic force between two current-carrying coils. For a current-carrying coil,since the distribution of magnetic field is firstly required for calculating the magnetic force on the current unit,previously researchers made great effort mainly on calculating the magnetic field of current-carrying coils. Some of them presented the analytic expression of the magnetic field of a current-carrying coil (or a permanent/electromagnetic magnet from coils) with a circular[12],rectangular[13] cross section,and some made the numerical simulation of the distribution of its magnetic field[14]. On these bases,the magnetic force between two current-carrying coils has been further studied. Babic and Akyel[15] and Robertson et al.[16] presented the analytic expression of the magnetic force between two thin coaxial coils and between a coaxial magnet and a thin coil. Furthermore, for the two coils with a limited horizontal misalign (whose axes are paralleled),Kim et al.[17] and Ren[18] calculated the magnetic force between each other. In fact,the misalignment in assembly design of the system and shift from the original position due to the imbalance of magnetic force in current-carrying operation,in some extent,are unavoidable. These factors can make current-carrying coils to be located at an arbitrary position and orientation between each other in the three-dimensional space,not just as the cases mentioned above in which two coils are the coaxial or translationally misaligned. Thus,for the practical design and safety operation of the magnet systems with current-carrying coils,it should be extremely significant to accurately calculate the magnetic force between the two coils with non-coplanar axes (actually these two coils have arbitrary spatial position and orientation between each other).
In this paper,based on Biot-Savart’s law,for the two current-carrying coils with noncoplanar axes,the analytic expressions of the magnetic field of a coil,and the magnetic force between each other are presented. On the verification of our approach,the variation of the magnetic force between the two current-carrying coils is comprehensively investigated. 2 Analytic calculation of magnetic force 2.1 Geometric configuration of problem
As shown in Fig. 1,Coils 1 and 2 with the symmetry axes I1 and I2,which are in noncoplanar, are at arbitrary relative positions. Without loss of generality,Coil 1 is fixed at the origin of coordinate (i.e.,the point O) and located in the xy-plane. The location and the orientation of Coil 2 can be determined by the coordinate of its center O′(xO′,yO′,zO′) and the angles of the plane of Coil 2 referring to the x- and y-axes (specifically noted below),respectively. The radii of Coils 1 and 2 are,respectively,r1 and r2,and the radius ratio is introduced as μ = r1/r2 (μ > 1). The current intensities of Coils 1 and 2 are I1 and I2,respectively.
In the O-xyz coordinate system,for the point P (xP,yP,zP ) on Coil 1,the coordinates are given as
 |
| Fig. 1 Configuration of two current-carrying circle coils with non-coplanar axes,where I1 and I2, symmetry axes of Coils 1 and 2,are in non-coplanar |
For the point P′ (xP′,yP′,zP′) (its vectro is noted as) on Coil 2 in the coordinate system,we can obtain
in which and A and B are the rotation operations of the angles α and β,which are the angles of the plane of Coil 2 referring to the x-axis and the y-axis,respectively.On above the geometric model,for rationally establishing the approach of the calculations of the magnetic field of a current-carrying coil and the magnetic force between the two coils, some basic assumptions have to be given as follows:
(i) The current in the coils keeps to be steady. Resistance loss of current-carrying coils is not taken account here. The magnetic coupling between two coils is not considered. Hence,the effect of the variation of the current in one coil on the other coil is neglected here.
(ii) The distance between the centers of the two current-carrying coils cannot be infinitely close to each other. Physically,the distance between the centers of two circle coils can be zero. However,mathematically,it may cause serious singularity in calculation.
(iii) The elastic deformation and dynamic behavior of current-carrying coils are not further taken into account in this study. Based on the geometric model shown in Fig. 1 and the above necessary assumptions,according to the rule of Ampere circulation and Biot-Savart’s law,the magnetic force of the coils with non-coplanar axes can be analytically obtained. For this aim,there are two basic steps of the spatial distribution of the magnetic field of Coil 1 and the magnetic force of Coil 2 in the magnetic field from Coil 1. 2.2 Magnetic field of Coil 1
For simplicity,the magnetic field of the point P′ (rP′,θP′,zP′) on Coil 2 induced from Coil 1 can be given in the cylindrical coordinate system as[17]
in which where K(k) and E(k) are,respectively,the complete elliptic integrals of the first and second kinds,and μ0 (the permeability of free space) is 4π × 10−7. In the O-xyz coordinate system, the magnetic field at the point P′(xP′,yP′,zP′ ) can be transformed as in which rP′ =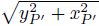 .
2.3 Magnetic force between two coils
.
2.3 Magnetic force between two coils
The magnetic force of the current unit I2dl of Coil 2 in the magnetic field induced from Coil 1 can be given by
in which dl =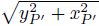 . Therefore,the projection of the x-,y-,and z-
axes of the current unit I2dl can be written by (I2dl)x,(I2dl)y,and (I2dl)z. Then,Eq. (7) in
cylindrical coordinates can be developed as
in which ei,ej,and ek are the unit vectors of the x-,y-,and z-axes. Thus,the magnetic force
between Coils 1 and 2 can be obtained as
3 Results and discussion
3.1 Verification of approach
. Therefore,the projection of the x-,y-,and z-
axes of the current unit I2dl can be written by (I2dl)x,(I2dl)y,and (I2dl)z. Then,Eq. (7) in
cylindrical coordinates can be developed as
in which ei,ej,and ek are the unit vectors of the x-,y-,and z-axes. Thus,the magnetic force
between Coils 1 and 2 can be obtained as
3 Results and discussion
3.1 Verification of approach
To veriFy the approach presented above,the case of the two current-carrying circle coils with parallel axes is considered,and the magnetic force between the coils will be further compared with those in the published work[17]. In this case,the planes of the two coils are parallel. The coordinate zO′ of Coil 2 is fixed,and the misaligned distance is limited just in the xy-plane. For simplicity,as shown in Fig. 2,the misaligned distance is just along the y-axis,noted as Δy. Then,the coordinate of the point P′ can be written as
 |
| Fig. 2 Two current-carrying circle coils with parallel axes,where l1 and l2,symmetry axes of Coils 1 and 2,are parallel,and distance between each other is noted as Δy |
After Eq. (10) is substituted into Eq. (4),the magnetic field of Coil 1 can be given by
in whichAccording to Eq. (8),dFy can be given as (I2dl)zBx−(I2dl)xBz = (I2r2sin θ)Bzdθ,and dFz along the z-axis is (I2dl)xBy − (I2dl)yBx = −(r2 sin θyP′/rP′ + r2 cos θxP′/rP′ )Brdθ. Thus,the y- and z-components of the magnetic forces (Fy and Fz) can be,respectively,given as
When Coils 1 and 2 have N1 and N2 turns,respectively,the magnetic force between the coils can be further obtained as[17]In calculation,r1 and r2 are chosen as 0.5m and 0.3m,respectively. The current intensities I1 and I2 are given as 10 A and 20 A,respectively. If zO′ is kept as 0.2m,we can obtain the variation of the magnetic force with the misaligned distance Δy. The calculation results of the magnetic forces Fy and Fz are listed in Tables 1 and 2,respectively.
As listed in Tables 1 and 2,though the calculation approach is somewhat different from that in Ref. [17],the calculation results are close to each other. The maximum error is 1.038% for the radial magnetic force and about 0.026% for the axial magnetic force. Thus,the comparison of the magnetic force verifies that our approach in this paper is exact and achieves enough accuracy.
 |
 |
It is noted here that,even Δy is zero (the first line and the first column in the two tables),
it does not mean that the distance of the center of Coil 2 away from that of Coil 1 is zero. For
the distance  zO′ is always kept as a nonzero constant.
3.2 Results and discussion
zO′ is always kept as a nonzero constant.
3.2 Results and discussion
Based on the geometric model shown in Fig. 1 and applying the analytic expression of the magnetic force between two current-carrying coils,we can further investigate the variation of the magnetic force between the two coils with the spatial relative position and the orientation of each other,which is very important not only for the design,but also for the safety operation of the related electromagnetic equipment with current-carrying coils. In the calculation below, r1 is chosen as 60mm (r2 can be determined by μ = r1/r2),and the current intensities I1 and I2 are given as 10 A and 20 A,respectively. Coil 1 is still supposed to be fixed at the origin of coordinate system O-xyz. As a result,the calculation results of the variation of the magnetic force between the two coils with the spatial relative position and the orientation of each other have been obtained as shown in Figs. 3-6.
The spatial variation of the components Fx,Fy,and Fz of the magnetic force with the
coordinate of the centre of Coil 2 in the xy-plane is shown in Fig. 3. It is found that the
variation of the components Fx and Fy with the coordinates xO′ and yO′ is almost monotone,
and it ranges from positive to negative,while the component Fz keeps always negative,its value
reaches the maximum at the distance about 2 mm from the center of Coil 1 (i.e.,the origin of
coordinate),and then decreases with the distance. Within a same spatial range,generally,the
magnitude of the component Fz is always much larger than those of the components Fx and
Fy. At a given height (for example,here zO′ is 30 mm),the misaligned distance in the xy-plane
results in considerable in-plane magnetic forces (i.e.,the components Fx and Fy). In fact,these
in-plane magnetic forces result in the restoring force,usually defined as Fr as  ,
which can make Coil 2 back to its original position. Figure 4 shows that the variation of the
restoring force with the distance between the centers of the coils in the xy-plane (defined as
,
which can make Coil 2 back to its original position. Figure 4 shows that the variation of the
restoring force with the distance between the centers of the coils in the xy-plane (defined as  It is found that the restoring force always has a peak value with the distance.
Before the peak,the restoring force increases with the distance,while decreases after the peak.
Besides,under the given size of Coil 1,the larger the radius ratio is,the smaller the restoring
force is. These results should be very helpful for safety control of the current-carrying coils to
be reset in electromagnetic systems.
It is found that the restoring force always has a peak value with the distance.
Before the peak,the restoring force increases with the distance,while decreases after the peak.
Besides,under the given size of Coil 1,the larger the radius ratio is,the smaller the restoring
force is. These results should be very helpful for safety control of the current-carrying coils to
be reset in electromagnetic systems.
 |
| Fig. 3 Variation of magnetic force components Fx,Fy,and Fz with center of Coil 2 when r1 = 60mm, r2 = 30mm,zO′ = 30mm,and α = β = 0 |
 |
Fig. 4 Variation of restoring force Fr with distance  in xy-plane in three cases of radius
ratio μ when zO′=30 mm,r1=60 mm,and α = β=0 in xy-plane in three cases of radius
ratio μ when zO′=30 mm,r1=60 mm,and α = β=0 |
For the given angles of α and β (here α = π/20 and β = π/10),the magnetic force with the coordinates yO′ and zO′ of the center of Coil 2 has been calculated and shown in Figs. 5 and 6, respectively. For simplicity,the x-coordinate of the center of Coil 2 is also assumed to be zero, that is,the movement of the center of Coil 2 is limited just in the yz-plane. As shown in Fig. 5, the components Fy and Fz are much larger than the component Fx,and the latter is close to zero. Obviously,the components Fy and Fz dominate. With the y-coordinate increasing,the component Fy decreases,while the component Fz increases in this case. In fact,practically,the restoring force (related to Fx and Fy) increases,while the magnitude of Fz decreases. Bedsides, once the size of Coil 1 is given,the larger the radius ratio μ is,the smaller the magnitude of the magnetic force is (here Fy and Fz are always minus). As shown in Fig. 6,under these given parameters,the component Fx is always positive,while the components Fy and Fz are negative. Just from their magnitudes,comparatively,the components Fy and Fz are larger,and with the z-coordinate increasing,all the components Fx,Fy,and Fz decrease. Furthermore,similarly as in Fig. 5,the larger the radius ratio is,the smaller all the components of the magnetic force are.
 |
| Fig. 5 Variation of magnetic force Fx,Fy,and Fz with yO′ (y-coordinate of center of Coil 2) in three cases of radius ratio μ when xO′ = 0mm,zO′ = 30mm,r1 = 60mm,α = π/20,and β = π/10 |
 |
| Fig. 1 Variation of magnetic force components Fx,Fy,and Fz with zO′ (z-coordinate of center of Coil 2) in three cases of radius ratio μ when xO′ = 0mm,yO′ =30 mm,r1 = 60mm,α = π/20,and β = π/10 |
To further investigate the variation of the magnetic force with the orientation of Coil 2,for simplicity,we set the center of Coil 2 at a given height,and on the symmetry axes I1 of Coil 1, and then just make the orientation of the plane of Coil 2 vary referring to the xy-plane. As a result,the variations of the magnetic force with the angles α and β are obtained and shown in Fig. 7. Compared with the results in Fig. 3,the variation of the magnetic force with the angles α and β is more distinct. The variations of the components Fx and Fy are symmetric referring to the angles α and β,respectively,and for the component Fz,it is centrosymmetric. As shown in Figs. 7(a) and (b),for the component Fx,it reaches zero when the angle β is equal to zero, and it increases with the angle β. The similar variation is for the component Fy with the angle α. The difference is that the component Fx varies not only with the angle β but also with the angle α. It can reach the extreme point (positive and negative) when the angle α is equal to zero. For the component Fy,it varies only with the angle α,almost not with the angle β. For the component Fz,it can reach the negative extreme point when both the angles α and β are zero,and monotonously increases when the angles α and β increase.
 |
| Fig. 7 Variation of magnetic force components Fx,Fy,and Fz with angles α and β (plane of Coil 2 referring to x- and y-axes,respectively) when xO′ = yO′ = 0mm,zO′ = 30mm,r1 = 60mm, and r2 = 30mm |
For a practical electromagnetic system with current-carrying coils,in the initial assembly and operation,the plane of the coil referring to others,usually has a misaligned angle,not always parallel with each other (here it means α = β = 0). To control the coil to be reset back to the original orientation,the moment on the coil from the magnetic force,which has the mechanical effect of rotation,is very important. As shown in Fig. 1,the moment M of Coil 2 from Coil 1 can be calculated as
in which dP′ is the vector of the point P′ on Coil 2 in the O-xyz coordinate system,dF is the magnetic force of the current unit of Coil 2 in the magnetic field from Coil 1. To characterize the rotation effect of the magnetic force on Coil 2 around the x- and y-axes,we also define the restoring moment Mr as in which Mx and My stand for the x- and y-components of moment,respectively.The variation of the restoring moment Mr with the angles α and β is calculated as shown in Fig. 8. Obviously,the variation of the moment Mr is symmetrical with the angles α and β. Specifically,the variation of the moment Mr has a saddle shape about the angle β. When both the angles β and α are close to zero,the moment Mr arrives to the minimum extrem point. With the angle β getting bigger,the moment Mr accordingly increases. Meanwhile,when the angle α is zero,Mr reaches the maximum extreme point,and when the angle α gets bigger,Mr decreases sharply.
 |
| Fig. 8 Variation of restoring moment Mr with angles α and β (plane of Coil 2 referring to x- and y-axes,respectively) when xO′ = yO′ = 0mm,zO′ = 30mm,r1 = 60mm,and r2 = 30mm |
For two current-carrying coils with non-coplanar axes,based on Biot-Savart’s law,the analytic expression of the magnetic force is presented. The comparison of the magnetic force verifies that the approach in this paper has enough exactness. Furthermore,the complete and deep investigation of the variation of the magnetic force shows that the magnetic force between the two coils is closely related to the size,the relative position,and the orientation of each other. Besides the statical magnetic force,for two current-carrying coils with non-coplanar axes,hopefully,the elastic deformation and dynamic behaviours of the coils due to the magnetic force should be further studied. These studies including that in this paper will be helpful for the design and safety operation of related electromagnetic equipment with current-carrying coils.
| [1] | Lee, J. J., Jo, Y. S., Hong, J. P., and Kwon, Y. K. Design of field coil for 100 hp class HTS motor considering operating current. IEEE Transactions on Applied Superconductivity, 13(2), 2214-2217 (2003) |
| [2] | Zheng, X. J., Wang, X. Z., and Zhou, Y. H. Magnetoelastic analysis of non-circular superconduct-ing partial torus. International Journal of Solids and Structures, 37(4), 563-576 (2000) |
| [3] | Friend, C. M., Miao, H. P., Huang, Y. B., Melhem, Z., Domptail, F., Meinesz, M., Hong, S., Young, E. A., and Yang, Y. F. The development of high field magnets utilizing Bi-2212 wind & react insert coils. IEEE Transactions on Applied Superconductivity, 20(3), 583-586 (2010) |
| [4] | Nomura, S., Ohata, Y., Hagita, T., Tsutsui, H., Tsuji-Iio, S., and Shimada, R. Helically wound coils for high field magnets. IEEE Transactions on Applied Superconductivity, 14(2), 709-712 (2004) |
| [5] | Schwartz, J., Effio, T., Liu, X. T., Le, Q. V., Mbaruku, A. L., Schneider-Muntau, H. J., Shen, T. M., Song, H. H., Trociewitz, U. P., Wang, X. R., and Weijers, H. W. High field superconducting solenoids via high temperature superconductors. IEEE Transactions on Applied Superconductivity, 18(2), 70-81 (2008) |
| [6] | Ling, J. Y., Voccio, J., Kim, Y., Hahn, S., Bascunan, J., Park, D. K., and Iwasa, Y. Monofil-ament MgB2 wire for a whole-body MRI magnet: superconducting joints and test coils. IEEE Transactions on Applied Superconductivity, 23(3), 6200304 (2013) |
| [7] | Amemiya, N. and Akachi, K. Magnetic field generated by shielding current in high T(c) supercon-ducting coils for NMR magnets. Superconductor Science and Technology, 21(9), 095001 (2008) |
| [8] | Huguet, M. and the ITER International Team and Participant Teams. The ITER magnets: prepa-ration for full size construction based on the results of the model coil programme. Nuclear Fusion, 43(5), 352-357 (2003) |
| [9] | Zhu, J. Y., Luo, W., Zhou, Y. H., and Zheng, X. J. Contact mechanical characteristics of Nb3Sn strands under transverse electromagnetic loads in the CICC cross-section. Superconductor Science and Technology, 25(12), 125011 (2012) |
| [10] | Xia, J., Yong, H. D., and Zhou, Y. H. A structural mechanics model for the 2-D mechanical char-acteristics of ITER cable-in-conduit conductor cable under transverse loads. IEEE Transactions on Applied Superconductivity, 23(5), 8401209 (2013) |
| [11] | Markiewicz, W. D., Larbalestier, D. C., Weijers, H. W., Voran, A. J., Pickard, K. W., Sheppard, W. R., Jaroszynski, J., Xu, A. X., Walsh, R. P., Lu, J., Gavrilin, A. V., and Noyes, P. D. Design of a superconducting 32 T magnet with REBCO high field coils. IEEE Transactions on Applied Superconductivity, 22(3), 4300704 (2012) |
| [12] | Ravaud, R., Lemarquand, G., Lemarquand, V., and Depollier, C. Analytical calculation of the magnetic field created by permanent-magnet rings. IEEE Transactions on Magnetics, 44(8), 1982- 1989 (2008) |
| [13] | Gou, X. F., Yang, Y., and Zheng, X. J. Analytic expression of magnetic field distribution of rectangular permanent magnets. Applied Mathematics and Mechanics (English Edition), 25(3), 297-306 (2004) DOI 10.1007/BF02437333 |
| [14] | Jiang, X. H. and Campbell, A. M. Numerical calculation of magnetic fields in melt processed YBCO magnets. IEEE Transactions on Applied Superconductivity, 7(2), 1213-1215 (1997) |
| [15] | Babic, S. I. and Akyel, C. Magnetic force calculation between thin coaxial circular coils in air. IEEE Transactions on Magnetics, 44(4), 445-452 (2008) |
| [16] | Robertson, W., Cazzolato, B., and Zander, A. A simplified force equation for coaxial cylindrical magnets and thin coils. IEEE Transactions on Magnetics, 47(8), 2045-2049 (2011) |
| [17] | Kim, K. B., Levi, E., Zabar, Z., and Birenbaum, L. Restoring force between two noncoaxial circular coils. IEEE Transactions on Magnetics, 32(2), 478-484 (1996) |
| [18] | Ren, Y. Magnetic force calculation between misaligned coils for a superconducting magnet. IEEE Transactions on Applied Superconductivity, 20(6), 2350-2353 (2010) |
 2015, Vol. 36
2015, Vol. 36



















