Shanghai University
Article Information
- Q. HUSSAIN, S. ASGHAR, T. HAYAT, A. ALSAEDI. 2015.
- Heat transfer analysis in peristaltic flow of MHD Jeffrey fluid with variable thermal conductivity
- J. Meteor. Res., 36(4): 499-516
- http://dx.doi.org/10.1007/s10483-015-1926-9
Article History
- Received 2014-04-11;
- in final form 2014-08-13
2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Faculty of Science, King Abdul Aziz University, Jeddah 21589, Saudi Arabia;
3. Department of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan
The study of peristaltic pumping of viscous and non-Newtonian fluids has received special attention in recent years. The word peristaltic comes from a Greek word “peristaltikos” which means clasping and compressing. The peristaltic transport is a mechanism of fluid transport from a region of lower pressure to high pressure by means of wave of area contraction/expansion travelling along a tube-like structure. Peristalsis is involved in the flow of urine from kidney to bladder through ureter,movement of food bolus in the alimentary canal,ovum transport in the female fallopian tube,transport of lymph in the lymphatic vessels,embryo motion in nonpregnant uterus,movement of semen in the vas deferens,bile movement in a bile duct,transport of spermatozoa in the cervical canal,and circulation of blood in the small blood vessels. In addition,the design of several technological devices is based upon the principle of peristaltic pumping. Mention may be made to blood pumps in heart-lung machines and finger and roller pumps for pumping of corrosive and toxic liquids in nuclear industry. Now,the literature on the peristaltic flow of viscous fluid through different assumptions is quite extensive (see Refs. [1,2,3,4,5] and some references therein).
It has been observed that many physiological and industrial fluids show a non-Newtonian behavior. Since there is no universal model which can describe the properties of all nonNewtonian fluids,several models have been proposed to explain the behavior of such fluids. The peristaltic mechanism of non-Newtonian fluids is quite prevalent in many applications,especially for intrauterine transport in non-pregnant uterus[6]. Radhakrishnamacharya[7] presented the long wavelength analysis for peristaltic transport of power law fluid. Siddiqui and Schwarz[8] studied the peristaltic pumping of a second-order fluid in tubes. Tsiklauri and Beresnev[9] examined the non-Newtonian effects on peristaltic transport of Maxwell fluid. Mekheimer[10] investigated the peristaltic flow of a couple-stress fluid in uniform and non-uniform channels. Hayat et al.[11] considered a problem of peristaltic transport of Johnson-Segalman fluid in a planar channel. A mathematical model for peristaltic transport of micropolar fluid in a tube was given by Srinivasacharya et al.[12] . Vajravelu et al.[13] made an attempt which deals with the peristalsis of Hershel-Bulkley fluid in an inclined tube. Tripathi[14] considered the OldroydB fluid model to study the peristaltic flow of chyme movement in small intestines. Ellahi et al.[15] discussed peristaltic transport of the Carreau fluid in a rectangular duct.
Biomagnetic fluid dynamics is quite a hot research area amongst the recent investigators. This is due to its applications in cancer tumor treatment,hyperthermia,reduction of blood during surgeries,etc. Also,considering blood as a biomagnetic fluid,it is now possible to control the blood pressure and its flow behavior by applying an appropriate magnetic field. The influence of the magnetic field may also be utilized as a blood pump for cardiac operations specifically for a disease in the stenosed artery. Hence,Mekheimer and El-Kot[16] examined the effects of magnetic field and Hall currents on blood flow through stenotic arteries. Elshahed and Haroun[17] studied the peristaltic transport of the magnetohydrodynamic (MHD) JohnsonSegalman fluid. Hayat and Ali[18, 19] investigated the MHD peristaltic flow of non-Newtonian fluids in a tube. In another paper,Hayat et al.[20] documented the influence of an induced magnetic field on the peristaltically induced flow of a Carreau fluid. Mekheimer et al.[21] studied the influence of the magnetic field on the peristaltic flow of a compressible Maxwell fluid in a microchannel with the porous medium. Peristaltic transport of the MHD Jeffrey fluid in an asymmetric channel was addressed by Kothandapani and Srinivas[22] . Pandey and Chaube[23] analyzed the effects of the magnetic field and the space porosity on the peristaltic flow of micropolar fluid. Recently,Tripathi and Bég[24] presented a magnetohydrodynamical study relevant to the digestive transport mechanism.
The study of heat transfer effect on peristaltic transport of blood has become quite interesting both from theoretical and experimental points of view,because the quantitative prediction of blood flow rate and heat generation is important for diagnosing blood circulation illness and for the noninvasive measurement of blood glucose. Research interest in the peristaltic flow of non-Newtonian fluids with heat transfer has increased substantially due to its numerous applications such as oxygenation,separation process in chemical industries,petroleum production,and polymer engineering. Some representative studies in this direction may be mentioned through the attempts[25, 26, 27, 28].
In all the studies mentioned above,the magnetic field is applied in a direction perpendicular to the flow. Very little has been said yet to the peristaltic flow in the presence of an inclined magnetic field[29, 30, 31, 32, 33, 34, 35] . Moveover,the peristaltic flow with heat transfer and an inclined magnetic field has not been studied yet even for viscous fluids. Therefore,it is of great interest to study the influence of an inclined magnetic field on peristaltic transport of a Jeffrey fluid with variable thermal conductivity. The present problem considers the Jeffrey fluid model which is significant among all other non-Newtonian models for physiological fluids,because it convertly reduces to a Newtonian model by taking λ1 = 0. The thermal conductivity of the fluid is assumed to vary with the temperature in a linear manner. The heat transport equation has been modified through viscous and Joule dissipations. The flow analysis has been conducted in the wave frame subject to long wavelength,low Reynolds number,and small thermal conductivity parameter. The effects of the inclination angle of magnetic field,the magnetic parameter,and the Jeffrey fluid parameter on peristaltic transport are analyzed. The effects of the thermal conductivity parameter,the inclination angle of magnetic field,the magnetic parameter,the Jeffrey fluid parameter,and the Brinkman number on the heat transfer process are also analyzed. The results obtained here are examined by plots and numerical values. 2 Mathematical model
Consider the two-dimensional flow of an incompressible Jeffrey fluid in an asymmetric channel. The channel walls are taken as flexible and non-conducting. It is further assumed that sinusoidal waves of small amplitudes propagate along the channel walls (see Fig. 1). The geometry of the walls is therefore given by
in which X and Y are the rectangular coordinates with X measured along the channel length, and Y is in the direction normal to channel walls,t is the time,c is the wave speed,λ is the wavelength,a1 is the upper wave amplitude,a2 is the lower wave amplitude,d1 + d2 is the channel width,and φ ∈ [0,π] is the phase difference. Moreover,ai,di(i = 1,2),and φ satisfy the condition It is assumed for the heat transfer process that the upper and lower channel walls are subject to the constant temperatures T0 and T1,respectively,and the temperature of the upper wall is less than that of the lower wall,i.e.,T0 < T1 . In addition,the fluid is electrically conducting in the presence of a uniform magnetic field B0 applied in a direction which makes an angle θ with the X-axis in the XY-plane. The contribution of the induced magnetic field has been ignored under the assumption of low magnetic Reynolds numbers. The effects of the imposed and induced electric fields are negligible. In view of such assumptions,the current density by Ohm’s law becomes J = σ[V × B0] (see Refs. [17],[36],and [37] for further details). If V= [U (X,Y,t),V(X,Y,t),0] is the velocity field vector,B0 = [B0 cos θ,B0 sin θ,0] is the magnetic flux density vector,and σ is the electrical conductivity of the fluid,then the Lorentz force vector takes the form |
| Fig. 1 Physical model |
The expressions of the Cauchy and the extra stress tensors τ and S in a Jeffrey fluid are given,respectively,by
in which P is the pressure,λ1 is the ratio of the relaxation time to the retardation time,λ2 is the retardation time,and µ is the fluid dynamic viscosity. The definition of the involved Rivlin-Ericksen tensor A1 is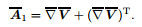
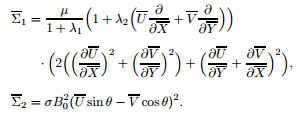
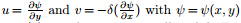 as the stream function,the incompressibility condition (7) vanishes automatically,while Eqs. (8)-(10) yield
with
Here,δ is the wave number,M is the magnetic parameter,ε is the thermal conductivity
parameter,Re is the Reynolds number,Pr is the Prandtl number,Ec is the Eckert number,
and Br = PrEc is the Brinkman number.
as the stream function,the incompressibility condition (7) vanishes automatically,while Eqs. (8)-(10) yield
with
Here,δ is the wave number,M is the magnetic parameter,ε is the thermal conductivity
parameter,Re is the Reynolds number,Pr is the Prandtl number,Ec is the Eckert number,
and Br = PrEc is the Brinkman number.
Invoking the long wavelength (δ → 0) and the low Reynolds number (Re → 0) approximations into Eqs. (14)-(16),we arrive at
where k(T) is the dimensionless thermal conductivity function.The dimensionless boundary conditions are
where F is the dimensionless time mean flow rate in the wave frame,which is defined by which can be further related with the dimensionless time mean flow rate in the fixed frame Q through The peristaltic walls in the dimensionless form can be written as in which α1 and α2are the amplitude ratios,and d is the channel width ratio given by Now,we have 3 Mathematical resultsEquations (20) and (21) yield the compatibility equation of the form
Solving Eq. (31) subject to the boundary conditions (23) and (24),one has The expression for the axial velocity is The pressure rise per wavelength ∆Pλ can be computed through in which dp/dx is the axial pressure gradient. It is given by It is clear that the closed form solution of the nonlinear equation (22) seems difficult. Therefore, it is of interest to construct the series solution (perturbation solution) in powers of small thermal conductivity parameter ε. For this purpose,we write where ε is the perturbation quantity. Collection of the coefficients of like powers of ε after inserting Eq. (36) into Eqs. (22) and (25) yields the following systems at zeroth- and first-orders. 3.1 Zeroth-order systemThe zeroth-order problem is
Using Eq. (32) and solving Eq. (37) subject to the conditions (38),we get with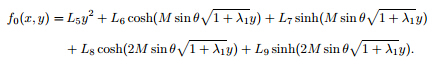
The problem at this order is
The solution of the above problem is where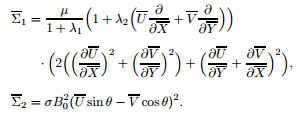
The heat transfer coefficient at the upper wall is
4 Numerical results and discussionThis section is aimed to study the important features of peristaltic mechanism and heat transfer under the influence of involved parameters such as θ (the inclination angle of magnetic field),M (the magnetic parameter),λ1 (the Jeffrey fluid parameter),ε (the thermal conductivity parameter),and Br (the Brinkman number). For this purpose,we prepare Fig. 2 for the pressure rise per wavelength ∆Pλ ,Fig. 3 for the axial pressure gradient dp/dx,Fig. 4 for the velocity field u,Fig. 5 for the temperature field T,and Figs. 6-8 for trapping. Note that we have performed numerical integration to compute the pressure rise per wavelength ∆Pλ . The values of geometric parameters are fixed as α1 = 0.5,α2 = 0.5,d = 1,and φ = π/2 in all the graphs and tables.
 |
| Fig. 2 Pressure drop ∆Pλ vs. Q |
 |
| Fig. 3 Axial pressure gradient dp/dx vs. x ∈ [−0.5,0.5] for Q =0.1 |
 |
| Fig. 4 Velocity distribution u vs. y for x = 0 and Q = 1.2 |
 |
| Fig. 5 Temperature distribution T vs. y for x = 0 and Q = −1.2 |
Figure 2 is prepared to analyze the effects of θ,M ,and λ1 on the pressure rise per wavelength ∆Pλ versus Q. The effects of the inclination of magnetic field θ can be seen through Fig. 2(a). It is clear that the pumping rate in the peristaltic pumping region (∆Pλ > 0) increases by increasing θ ∈ [0,π/2]. However,it starts to decrease after appropriately choosing ∆Pλ > 0. In the augmented pumping region (∆Pλ < 0),the pumping rate decreases when θ ∈ [0,π/2] increases. It is interesting to mention here that the inclined magnetic field for θ ∈ [0,π/2] shows an opposite effect on the pumping performance when compared with θ ∈ [π/2,π]. The intervals for the flow rate Q where ∆Pλ > 0 and ∆Pλ < 0 are given in Table 1-3. Here,we notice that the length of the interval of Q where ∆Pλ > 0 decreases for θ ∈ [0,π/2],while it increases for θ ∈ [π/2,π]. Figure 2(b) elucidates the effect of the magnetic parameter M on ∆Pλ . It is noted that,in the peristaltic pumping region (∆Pλ > 0),the pumping rate is an increasing function of M ,whereas it becomes a decreasing function of M after appropriately choosing ∆Pλ > 0. The later behavior of pumping performance remains true in the augmented pumping region (∆Pλ < 0). An increase in M decreases the length of interval of Q against which ∆Pλ > 0. However,the length of interval of Q against which ∆Pλ < 0 increases when M increases (see Table 2). The influence of the Jeffrey fluid parameter λ1 on ∆Pλ is shown through Fig. 2(c). It is observed that the pumping rate fluid parameter λ1 is increased. In this case,the length of the interval for the flow rate Q where ∆Pλ > 0 decreases when changing from Newtonian fluid to Jeffrey fluid (see Table 3).
Figure 3 presents the variation of pressure gradient dp/dx over one wavelength x ∈ [−0.5,0.5] for various values of θ,M ,and λ1 . The graphs of pressure gradient dp/dx for different values of θ are displayed in Fig. 3(a). It is evident that,as θ increases from 0 to π/2,the pressure gradient dp/dx decreases in the interval x ∈ [−0.4,0.15],whilst it increases in the interval x ∈ [−0.5,−0.4] ∪ [0.15,0.5]. This behavior of dp/dx becomes opposite when θ increases from π/2 to π. The plots of dp/dx for various values of magnetic parameter M are drawn in Fig. 3(b). It discloses that an increment in M results in a decrease in dp/dx for x ∈ [−0.4,0.15] and an increase for x ∈ [−0.5,−0.4] ∪ [0.15,0.5]. Figure 3(c) is made to study the behavior of dp/dx via various values of the Jeffrey fluid parameter λ1 . This graph clearly indicates that the pressure gradient dp/dx is an increasing function of λ1 for x ∈ [−0.4,0.15]. However,it is a decreasing function of λ1 for x ∈ [−0.5,−0.4] ∪ [0.15,0.5].
Figure 4 is made to see the variations of θ,M,and λ1 on the axial velocity u versus y. Figure 4(a) shows the variation in u via the inclination θ of the magnetic field. It is observed that the amplitude of the velocity u decreases when θ lies in 0 < θ < π/2 and increases when θ lies in π/2 < θ < π. We observe that the contribution of the second term on the left-hand side of Eq. (28),towards the velocity,depends upon the value of sin θ in the range 0 < θ < π. For increasing values of θ in 0 < θ < π/2,sin θ increases,and the value of this term decreases (because of the negative sign). Hence,the velocity decreases in this range of angle θ. However, when π/2 < θ < π,sin θ decreases,and the value of this term increases. Thus,the velocity increases in this range of angle θ. The effect of the magnetic parameter M on the velocity u is displayed in Fig. 4(b). This graph illustrates that an increase in M leads to a reduction in the amplitude of velocity u. The velocity profiles u for different values of λ1 are sketched in Fig. 4(c). It is clear that the effect of the Jeffrey fluid parameter λ1 is to decrease the amplitude of velocity u.
The effects of θ,M,ε,λ1,and Br on the heat transfer process can be analyzed through Fig. 5. It is clear from Fig. 5(a) that the temperature T increases for θ ∈ [0,π/2],whilst it decreases for θ ∈ [π/2,π]. Figure 5(b) is made to observe the effect of the magnetic parameter M on the temperature T. Here,an increase in M shows an enhancement in the temperature T ,which leads to a conclusion that the temperature in the hydromagnetic fluid is higher than that in the hydrodynamic fluid. The effect of the thermal conductivity parameter ε on the temperature T is depicted in Fig. 5(c). It reveals that an increase in ε yields a decrease in T . Figure 5(d) discusses the behavior of the Jeffrey fluid parameter λ1 on the temperature T . This graph illustrates that the temperature T decreases as a result of increasing λ1 . The variation of temperature T with increasing Br is shown in Fig. 5(e). It is obvious from Fig. 5(e) that the temperature T increases when the effects of viscous and Joule dissipations are taken into account.
Tables 4-7 present the values of the heat transfer coefficient Z at the upper wall for various values of θ,M ,ε,λ1 ,and Br. These tables witness that the effect of inclined magnetic field for θ ∈ [0,π/2] is to increase the heat transfer coefficient Z for both constant and variable thermal conductivity fluids. However,the opposite is true for θ ∈ [π/2,π]. The value of the heat transfer coefficient Z is greater for the hydromagnetic fluid in comparison to the hydrodynamic fluid. The value of the heat transfer coefficient Z decreases when we move from the constant thermal conductivity fluid to the variable thermal conductivity fluid. We further observe that the value of the heat transfer coefficient Z is smaller for the Jeffrey fluid in comparison to the Newtonian fluid. Moreover,the consideration of the viscous and Joule dissipations amounts to an increase in the value of the heat transfer coefficient Z .
 |
 |
 |
 |
Figures 6-8 are given to discuss the variations in the size of the trapped bolus for various values of θ,M ,and λ1 . Figure 6 concludes that an increase in the inclination angle of magnetic field θ from 0 to π/2 shows a decrease in the size of trapped bolus. Moreover,the size of trapped bolus increases as we increase the value of θ from π/2 to π. Figure 7 portrays that the trapped bolus is less in size for the hydromagnetic fluid in comparison to the hydrodynamic fluid. In fact,the hydromagnetic characteristics arises because of an applied magnetic field. Consequently,the Lorentz force acts as a retarding force. This helps in reducing the size of trapped bolus. It is clearly shown in Fig. 8 that the trapped bolus decreases in size when the Jeffrey fluid parameter λ1 increases. The trapped bolus is smaller for the Jeffrey fluid in comparison to the Newtonian fluid.
 |
| Fig. 6 Influence of θ on trapping with Q = 1.48,M = 1.2,and λ1 = 0.5 |
 |
| Fig. 7 Influence of M on trapping with Q = 1.48,θ = π/4,and λ1 = 1 |
 |
| Fig. 8 Influence of λ1 on trapping with Q = 1.48,θ = π/4,and M = 1 |
The heat transfer analysis in a peristaltically induced flow of a Jeffrey fluid with variable thermal conductivity is performed under the influence of an inclined magnetic field. The pressure rise per wavelength is studied numerically. The effects of the involved parameters are analyzed and discussed with the help of graphs. The main points are listed below.
(i) The behavior of the inclined magnetic field for θ ∈ [π/2,π] is opposite compared with that of θ ∈ [0,π/2].
(ii) The length of interval for the flow rate Q against which ∆Pλ > 0 decreases by increasing θ ∈ [0,π/2],M ,and λ1 .
(iii) The magnitude of dp/dx increases as a result of increasing θ ∈ [0,π,2] and M ,whilst it decreases when λ1 increases.
(iv) An increase in θ ∈ [0,π/2],M ,and λ1 yields a decrease in the amplitude of velocity u.
(v) The effect of the inclined magnetic field for θ ∈ [0,π/2] is to increase the temperature T. However,it decreases by increasing ε. The temperature in the hydromagnetic (Newtonian) fluid is greater in comparison to the hydrodynamic (Jeffrey) fluid.
(vi) The value of the heat transfer coefficient Z increases due to an increase in θ ∈ [0,π/2], M,ε,and Br,whereas it decreases as λ1 increases.
(vii) The trapped bolus is greater in size for the case of the inclined magnetic field (θ ≠ π/2) when compared with the transverse magnetic field (θ = π/2). Moreover,the size of the trapped bolus decreases as a result of increasing M and λ1. Appendix A
Here,we include the values of Ai (i = 1,2,...,8) and Li (i = 1,2,...,20).
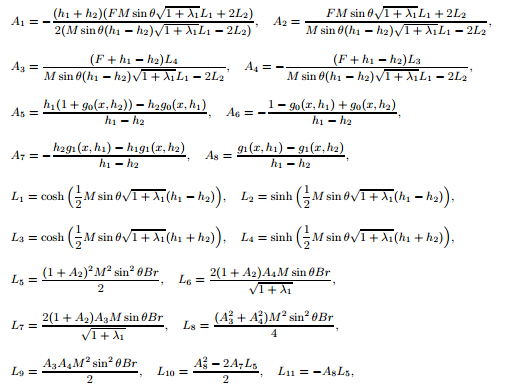
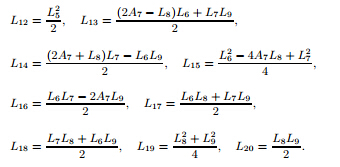
| [1] | Shapiro, A. H., Jaffrin, M. Y., and Weinberg, S. L. Peristaltic pumping with long wavelength at low Reynolds numbers. Journal of Fluid Mechanics, 37, 799-825 (1969) |
| [2] | Mishra, M. and Rao, A. R. Peristaltic transport of a Newtonian fluid in an asymmetric channel. Zeitschrift für Angewandte Mathematik und Physik, 54, 532-550 (2003) |
| [3] | Kothandapani, M. and Srinivas, S. Non-linear peristaltic transport of a Newtonian fluid in an inclined asymmetric channel through a porous medium. Physics Letters A, 372, 1265-1276 (2008) |
| [4] | Tripathi, D. A mathematical model for the movement of food bolus of varying viscosities through the esophagus. Acta Astronautica, 69, 429-439 (2011) |
| [5] | Mekheimer, K. S., Abd elmaboud, Y., and Abdellateef, A. I. Peristaltic transport through eccentric cylinders: mathematical model. Applied Bionics and Biomechanics, 10, 19-27 (2013) |
| [6] | Eytan, O. and Elad, D. Analysis of intra-uterine fluid motion induced by uterine contractions. Bulletin of Mathematical Biology, 61, 221-238 (1999) |
| [7] | Radhakrishnamacharya, G. Long wavelength approximation to peristaltic motion of power law fluid. Rheologica Acta, 21, 30-35 (1982) |
| [8] | Siddiqui, A. M. and Schwarz, W. H. Peristaltic flow of a second order fluid in tubes. Journal of Non-Newtonian Fluid Mechanics, 53, 257-284 (1994) |
| [9] | Tsiklauri, D. and Beresnev, I. Non-Newtonian effects in the peristaltic flow of a Maxwell fluid. Physical Review E, 64, 036303 (2001) |
| [10] | Mekheimer, K. S. Peristaltic transport of a couple-stress fluid in a uniform and non-uniform channels. Biorheology, 39, 755-765 (2002) |
| [11] | Hayat, T., Wang, Y., Siddiqui, A. M., and Hutter, K. Peristaltic motion of a Johnson-Segalman fluid in a plannar channel. Mathematical Problems in Engineering, 1, 1-23 (2003) |
| [12] | Srinivasacharya, D., Mishra, M., and Ramachandra, A. R. Peristaltic pumping of a micropolar fluid. Acta Mechanica, 161, 165-178 (2003) |
| [13] | Vajravelu, K., Sreenadh, S., and Babu, V. R. Peristaltic transport of a Hershel-Bulkley fluid in an inclined tube. International Journal of Non-Linear Mechanics, 40, 83-90 (2005) |
| [14] | Tripathi, D. A mathematical model for the peristaltic flow of chyme movement in small intestine. Mathematical Biosciences, 233, 90-97 (2011) |
| [15] | Ellahi, R., Riaz, A., Nadeem, S., and Ali, M. Peristaltic flow of Carreau fluid in a rectangular duct through a porous medium. Mathematical Problems in Engineering, 2012, 329639 (2012) |
| [16] | Mekheimer, K. S. and El-Kot, M. A. Influence of magnetic field and Hall currents on blood flow through a stenotic artery. Applied Mathematics and Mechanics (English Edition), 29(8), 1093- 1104 (2008) DOI 10.1007/s10483-008-0813-x |
| [17] | Elshahed, M. and Haroun, M. H. Peristaltic transport of Johnson-Segalman fluid under effect of a magnetic field. Mathematical Problems in Engineering, 2005, 663-677 (2005) |
| [18] | Hayat, T. and Ali, N. Peristaltically induced motion of a MHD third grade fluid in a deformable tube. Physica A, 370, 225-239 (2006) |
| [19] | Hayat, T. and Ali, N. A mathematical description of peristaltic hydromagnetic flow in a tube. Applied Mathematics and Computation, 188, 1491-1502 (2007) |
| [20] | Hayat, T., Saleem, N., and Ali, N. Effect of induced magnetic field on peristaltic transport of a Carreau fluid. Communications in Nonlinear Science and Numerical Simulation, 15, 2407-2423 (2010) |
| [21] | Mekheimer, K. S., Komy, S. R., and Abdelsalam, S. I. Simultaneous effects of magnetic field and space porosity on compressible Maxwell fluid transport induced by a surface acoustic wave in a microchannel. Chinese Physics B, 22, 124702 (2013) |
| [22] | Kothandapani, M. and Srinivas, S. Peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel. International Journal of Non-Linear Mechanics, 43, 915-924 (2008) |
| [23] | Pandey, S. K. and Chaube, M. K. Peristaltic flow of a micropolar fluid through a porous medium in the presence of an external magnetic field. Communications in Nonlinear Science and Numerical Simulation, 16, 3591-3601 (2011) |
| [24] | Tripathi, D. and Bég, O. A. Transient magneto-peristaltic flow of couple stress biofluids: a magneto-hydro-dynamical study on digestive transport phenomena. Mathematical Biosciences, 246, 72-83 (2013) |
| [25] | Ogulu, A. Effect of heat generation on low Reynolds number fluid and mass transport in a single lymphatic blood vessel with uniform magnetic field. International Communications in Heat and Mass Transfer, 33, 790-799 (2006) |
| [26] | Eldabe, N. T. M., El-Sayed, M. F., Ghaly, A. Y., and Sayed, M. H. Mixed convective heat and mass transfer in a non-Newtonian fluid at a peristaltic surface with temperature dependent viscosity. Archive of Applied Mechanics, 78, 599-624 (2007) |
| [27] | Hayat, T. and Hina, S. The influence of wall properties on the MHD peristaltic flow of a Maxwell fluid with heat and mass transfer. Nonlinear Analysis: Real World Applications, 11, 3155-3169 (2010) |
| [28] | Abd Elmaboud, Y., Mekheimer, K. S., and Abdellateef, A. I. Thermal properties of couple-stress fluid flow in an asymmetric channel with peristalsis. Journal of Heat Transfer, 135, 044502 (2013) |
| [29] | Seth, G. S. and Ghosh, S. K. Unsteady hydromagnetic flow in a rotating channel in the presence of inclined magnetic field. International Journal of Engineering Science, 24, 1183-1193 (1986) |
| [30] | Ghosh, S. K. A note on steady and unsteady hydromagnetic flow in a rotating channel in the presence of inclined magnetic field. International Journal of Engineering Science, 29, 1013-1016 (1991) |
| [31] | Elshehawey, E. F., Elbarbary, E. M. E., and Elgazery, N. S. Effect of inclined magnetic field on magneto fluid flow through a porous medium between two inclined wavy porous plates (numerical study). Applied Mathematics and Computation, 135, 85-103 (2003) |
| [32] | Guria, M., Das, S., Jana, R. N., and Ghosh, S. K. Oscillatory Couette flow in the presence of an inclined magnetic field. Meccanica, 44, 555-564 (2009) |
| [33] | Bég, O. A., Sim, L., Zueco, J., and Bhargava, R. Numerical study of magnetohydrody-namic viscous plasma flow in rotating porous media with Hall currents and inclined magnetic field influence. Communications in Nonlinear Science and Numerical Simulation, 15, 345-359 (2010) |
| [34] | Nadeem, S. and Akram, S. Influence of inclined magnetic field on peristaltic flow of a Williamson fluid model in an inclined symmetric or asymmetric channel. Mathematical and Computer Mod-elling, 52, 107-119 (2010) |
| [35] | Noreen, S., Hayat, T., Alsaedi, A., and Qasim, M. Mixed convection heat and mass transfer in peristaltic flow with chemical reaction and inclined magnetic field. Indian Journal of Physics, 87, 889-896 (2013) |
| [36] | Kumari, A. V. R. and Radhakrishnamacharya, G. Effect of slip and mangetic field on peristaltic flow in an inclined channel with wall effects. International Journal of Biomathematics, 5, 1250015 (2012) |
| [37] | Nadeem, S. and Akram, S. Heat transfer in a peristaltic flow of MHD fluid with partial slip. Communications in Nonlinear Science and Numerical Simulation, 15, 312-321 (2010) |
| [38] | Chiam, T. C. Heat transfer in a fluid with variable thermal conductivity over a linear stretching sheet. Acta Mechanica, 129, 63-72 (1998) |
 2015, Vol. 36
2015, Vol. 36


































