Shanghai University
Article Information
- Jinglei XU, Zhengguang TU, Ning HU. 2015.
- Rotation invariant constitutive relation for Reynolds stress structure parameter
- J. Meteor. Res., 36(4): 517-522
- http://dx.doi.org/10.1007/s10483-015-1927-9
Article History
- Received 2013-10-29;
- in final form 2014-08-12
2. The 9th Designing of China Aerospace Science Industry Corporation, Wuhan 430000, China;
3. China Academy of Aerospace Aerodynamics, Beijing 100074, China
In the past forty years,hundreds of empirical turbulence models have been developed. How- ever,a model that is suitable for all (or even most) flows does not exist. In fact,there are six unknown Reynolds stresses in the Reynolds averaged Navier-Stokes (RANS) equation,and once they are properly closed,correct solutions can be obtained. Obviously,the current turbulence models have not achieved this goal. The calibration of empirical coefficients and the construction of turbulent scale equations,which influence the fluid dynamics[1],can easily bring in inaccuracy. The Reynolds stress constitution representing the kinematic relation is easier to model,but it brings more inaccuracy for the present models. For example,the eddy viscosity model (EVM) simply assumes that the Reynolds stress is proportional to the strain rate of the mean flow, i.e.,the eddy viscosity,which is widely used in industry,but this closure can only capture the Reynolds shear stress so as to describe the shear flows. The Reynolds stress anisotropy is thus ignored,and once the Reynolds normal stresses interfere with the mean flow (such as the shock- wave,the streamline curvature,and the separation),the accuracy of the model decreases rapidly.
The nonlinear eddy viscosity model (NLEVM) as well as the explicit algebraic stress model (EASM) are improvements of the EVM,which are formally the high-order Taylor expansion of the Reynolds stress to strain rate,and in this way,some Reynolds stress anisotropy is preserved. However,a recognized third-order NLEVM[2] with high-performance is not able to capture the most simple wall bounded flow,i,e.,the normal turbulent stresses in channel flows. People have made great efforts to model Reynolds stress anisotropy by introducing additional second-order invariant A2[3] of the stress anisotropy and even Lumley’s stress flatness factor A[4, 5, 6, 7] involving third-order invariants to capture the anisotropy,and good predictions have been achieved in the simulation of turbulent channel flows. Since A2 and A are functions of multiple unknown second-order tensors,the transport equations of which will generate more unclosed higher-order terms,the model form is extremely complex,and more artificial factors and limited sample data will be inevitably added in. The second-moment closure[8] and the EASM[9] are also developed to describe Reynolds stress anisotropy,in which additional trans- port equations are not necessary,but empirical coefficients and assumptions must be made for closure. As a result,the models which have accounted for near-wall anisotropy perform better than the ordinary NLEVM and EASM in the flows for calibration,but not always better when facing complex real-life turbulence. In addition to the higher-order tensors,the introduction of A and A2 transport equations also enhances numerical stiffness and restricts the applications.
We feel that the difficulty to capture Reynolds stress anisotropy lies in the loss of impor- tant information for closure. For example,the k-x series model is the mainstream of EVMs. However,k,which is the summation of three second-order statistics,wipes out much useful information. It is difficult to decompose k into six second-order statistical Reynolds stresses, because k only provides the velocity scale in the model. An extra scale x (such as ε and ω) is needed to construct the eddy viscosity,and supplements such as the Boussinesq assumption must be made to propose the Reynolds stress. Thus,insufficient gathered information leads to difficulties in closing the RANS equations. 2 Theory
In the v2-f model,Durbin[10] argued that the velocity v2 vertical to streamlines can better describe the damping of near-wall turbulence transport than k,and by using v2,the component of k,the artificial damping functions are eliminated,which supports the importance of the abundance of turbulence information. Since higher-order statistics contain much less in- formation than lower-order statistics,it is clearly easier to organize and model higher-order statistics by lower-order statistics. Another benefit is that the transport of first-order statistics only generates second unclosed terms[11],which are strongly correlated to the Reynolds stresses or even are exactly the Reynolds stresses. In fact,there is one model that adopts the first-order statistics[12]. It contains zero empirical coefficients,and many works[13, 14, 15] have shown that it can handle various types of turbulence well. However,the Reynolds normal stress anisotropy is not serious validated. This section tries to explore a relation between the Reynolds normal stress and the first-order statistics using the direct numerical simulation (DNS) data as a prior investigation. Assuming that ui is the instantaneous velocity,the fluctuation is
in which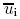 is the ensemble averaged velocity,i.e.,
where N represents all the possible solutions of the N-S equations. The positive fluctuating
velocity samples are collected to one group and averaged as
The remaining velocity samples are also averaged as
The ensemble average,
is actually 0,in which M+ = N+/N and M− = N−/N. Also,M+ +M− = 1. Now,we define
where
is the ensemble averaged velocity,i.e.,
where N represents all the possible solutions of the N-S equations. The positive fluctuating
velocity samples are collected to one group and averaged as
The remaining velocity samples are also averaged as
The ensemble average,
is actually 0,in which M+ = N+/N and M− = N−/N. Also,M+ +M− = 1. Now,we define
where 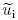 is the drift velocity,which is an example of the first-order statistics. Under the ergodic
hypothesis,the statistical analysis of the DNS data finds that,in a fully developed turbulence
region (y+ > 100 ),positive and negative fluctuations each take about 50%,whereas positive
and negative fluctuations take about 40% and 60%,respectively,very near wall,reaching the
maximum asymmetry. It is worth noting that when doing the statistics,the divisions of the
two groups for u,v,and w are different. The Reynolds shear stress is closely related to the
mean strain,since Boussinesq’s eddy viscosity assumption can often describe the Reynolds shear
stress well. For turbulent channel flows,if Boussinesq’s assumption is used,three normal mean
strain rates are zero,and thus three normal Reynolds stresses are zero,too. Obviously,the
Reynolds stress and the strain rate have little relevance. The NLEVM can capture some stress
anisotropy,because the influence of the shear strain is transferred to the Reynolds stress via the
formula of nonlinear constitutive relation. This paper argues that the Reynolds stresses have
little interaction with mean strains of averaged flows,and the essence is the autocorrelations
of the fluctuating velocity itself. The correlation is too strong to allow other factors to get
involved. Therefore,it is more appropriate to model with the first-order statistics. With the
belief of autocorrelation domination,the relationship of the Reynolds normal stress and the
drift velocity is conjectured as
where k is the turbulent kinetic energy,and the capital I implies no tensor summation. By
using drifting velocities,three Reynolds normal stresses can be decomposed from the turbulent
kinetic energy. Equation (7) can be written as
The parameter Rssp in Eq. (8) may be called as the Reynolds stress structure parameter (RSSP)
and would reveal some basic property for the turbulent velocity fields in the future. The two
equations will be assessed by the DNS data of the turbulent channel flows in the next section.
3 Statistics of DNS data
is the drift velocity,which is an example of the first-order statistics. Under the ergodic
hypothesis,the statistical analysis of the DNS data finds that,in a fully developed turbulence
region (y+ > 100 ),positive and negative fluctuations each take about 50%,whereas positive
and negative fluctuations take about 40% and 60%,respectively,very near wall,reaching the
maximum asymmetry. It is worth noting that when doing the statistics,the divisions of the
two groups for u,v,and w are different. The Reynolds shear stress is closely related to the
mean strain,since Boussinesq’s eddy viscosity assumption can often describe the Reynolds shear
stress well. For turbulent channel flows,if Boussinesq’s assumption is used,three normal mean
strain rates are zero,and thus three normal Reynolds stresses are zero,too. Obviously,the
Reynolds stress and the strain rate have little relevance. The NLEVM can capture some stress
anisotropy,because the influence of the shear strain is transferred to the Reynolds stress via the
formula of nonlinear constitutive relation. This paper argues that the Reynolds stresses have
little interaction with mean strains of averaged flows,and the essence is the autocorrelations
of the fluctuating velocity itself. The correlation is too strong to allow other factors to get
involved. Therefore,it is more appropriate to model with the first-order statistics. With the
belief of autocorrelation domination,the relationship of the Reynolds normal stress and the
drift velocity is conjectured as
where k is the turbulent kinetic energy,and the capital I implies no tensor summation. By
using drifting velocities,three Reynolds normal stresses can be decomposed from the turbulent
kinetic energy. Equation (7) can be written as
The parameter Rssp in Eq. (8) may be called as the Reynolds stress structure parameter (RSSP)
and would reveal some basic property for the turbulent velocity fields in the future. The two
equations will be assessed by the DNS data of the turbulent channel flows in the next section.
3 Statistics of DNS dataThe spectral method is used to simulate incompressible the turbulent channel flow at Reτ = 180. The periodic boundary condition is used in the streamwise (x-) and the span- wise (z-) directions,and the periods are 4πδ and 2πδ,respectively (δ is the channel half- width). The non-slip boundary condition is imposed on the wall. The dimension of the mesh is Nx × Ny × Nz = 128 × 129 × 128. There are 10 flow fields for statistic in total. Therefore, the number of the samples is 128 × 128 × 10 = 163 840.
Figure 1 presents the comparison of the DNS and the log-law. It is clear in Fig. 2 that the Reynolds normal stresses calculated by Eq. (7) are almost identical to the DNS statistics, which conforms applicability of this constitutive relation. The RSSP plotted in Fig. 3 shows the distributed percentage of the first-order statistics,which matches well with that of the Reynolds normal stresses,showing that the RSSP is a good structural ensemble function[16]. However,unlike the turbulent kinetic energy,the drift velocity in Eq. (7) is not a coordinate invariant,which may not be suitable for constructing a turbulence model. In order to dispel this doubt,the following will rotate the coordinate system and then verify whether Eq. (7) is feasible. Figure 4 shows the distribution of Reynolds normal stresses after the rotation of coordinate system counter-clockwise around the z-,x-,and y-axes at angels of 15◦,30◦,45◦, 60◦,and 75◦,respectively. When rotating around the z-axis at these angles,the x- and y-axes have swept all four quadrants of the O-xy coordinate system,and the situation is the same for rotating around the x-axis and the y-axis. Thus,after arbitrary rotation,the predictions of Eq. (7) can be inferred to match the DNS data very well. A conclusion can be drawn that estab- lishing a turbulence model with the first-order statistics as the basic element is quite feasible.
 |
| Fig. 1 Mean velocity in wall normal direction |
 |
| Fig. 2 Distribution of Reynolds stress |
 |
| Fig. 3 Distribution of RSSP |
 |
| Fig. 4 Reynolds stress distributions in different coordinates |
In this paper,a new concept Reynolds stress constitutive relation is proposed. It models the Reynolds normal stresses with the first-order statistics of velocity instead of the mean strain rate. The formula is quite concise and direct. The DNS simulation of turbulent channel flow is performed at Reτ = 180 for the latter statistical investigation. In all the coordinate systems for validation,the predicted Reynolds normal stresses by the formula agree precisely with the DNS data,which has proven the close correlation between the Reynolds normal stress and the autocorrelation of fluctuated velocities. The high-fidelity performance of the Reynolds stress constitutive relation in channel wall turbulence benefits from introducing the first-order drift velocity which contains high-density information. The new constitutive relation is expected to have wide applicability,which deserves further validation in other benchmark turbulent flows. The definition of drifting velocity is not unique,so are the transport equations,which are not developed in the present work. Nevertheless,constructing a turbulence model based on this constitutive formula is an easy approach to improve the existing turbulence models. on this constitutive formula is an easy approach to improve the existing turbulence models.
| [1] | Gatski, T. B. and Jongen, T. Nonlinear eddy viscosity and algebraic stress models for solving complex turbulent flows. Progress in Aerospace Sciences, 36(8), 655-682 (2000) |
| [2] | Craft, T. J., Launder, B. E., and Suga, K. Development and application of a cubic eddy-viscosity model of turbulence. International Journal of Heat and Fluid Flow, 17, 108-115 (1996) |
| [3] | Craft, T. J., Launder, B. E., and Suga, K. Prediction of turbulent transitional phenomena with a nonlinear model. International Journal of Heat and Fluid Flow, 18, 15-28 (1997) |
| [4] | Suga, K. and Abe, K. Nonlinear eddy viscosity modelling for turbulence and heat transfer near wall and shear-free boundaries. International Journal of Heat and Fluid Flow, 21, 37-48 (2000) |
| [5] | Abe, K., Jang, Y. J., and Leschziner, M. A. An investigation of wall-anisotropy expressions and length-scale equations for non-linear eddy-viscosity models. International Journal of Heat and Fluid Flow, 24(2), 181-198 (2003) |
| [6] | Abe, K. An improved anisotropy-resolving subgrid-scale model with the aid of a scale-similarity modeling concept. International Journal of Heat and Fluid Flow, 39, 42-52 (2013) |
| [7] | Ohtsuka, T. and Abe, K. On the role of an anisotropy-resolving extra term for a subgrid-scale model in near-wall turbulence. Journal of Computational Science and Technology, 7(3), 410-425 (2013) |
| [8] | Gerolymos, G. A., Lo, C., Vallet, I., and Younis, B. A. Term-by-term analysis of near-wall second-moment closures. AIAA Journal, 50(12), 2848-2864 (2012) |
| [9] | Wallin, S. and Johansson, A. V. An explicit algebraic Reynolds stress model for incompressible and compressible turbulent flows. Journal of Fluid Mechanics, 403(1), 89-132 (2000) |
| [10] | Durbin, P. Separated flow computations with the k-ε-v2 model. AIAA Journal, 33(4), 659-664 (1995) |
| [11] | Gao, G. and Xu, J. L. A partial average based study of compressible turbulent flows. International Journal of Mechanic Systems Engineering, 3(1), 20-35 (2013) |
| [12] | Gao, G. and Yong, Y. Partial-average-based equations of incompressible turbulent flow. International Journal of Non-Linear Mechanics, 39(9), 1407-1419 (2004) |
| [13] | Gao, G., Zhang, C. X., and Yan, W. H. Numerical study of compression corner flow field using Gao-Yong turbulence model (in Chinese). Journal of Aerospace Power, 27(1), 124-128 (2012) |
| [14] | Gao, G., Jiang, L., and Gao, L. Calculation of wing-body junction flow using Gao-Yong turbulence equations (in Chinese). Journal of Aerospace Power, 38(10), 1271-1274 (2012) |
| [15] | Gao, L., Gao, G., and Jiang, L. Numerical simulation of separated turbulent flow using Gao-Yong turbulent model (in Chinese). Journal of Aerospace Power, 39(5), 1-5 (2013) |
| [16] | She, Z. S., Hu, N., andWu, Y. Structural ensemble dynamics based closure model for wall-bounded turbulent flow. Acta Mechanica Sinica, 25(5), 731-736 (2009) |
 2015, Vol. 36
2015, Vol. 36










