Shanghai University
Article Information
- T. ANTCZAK. 2015.
- Exactness of penalization for exact minimax penalty function method in nonconvex programming
- J. Meteor. Res., 36(4): 541-556
- http://dx.doi.org/10.1007/s10483-015-1929-9
Article History
- Received 2014-01-23;
- in final form 2014-10-03
The extremum problem considered in this paper is a general nonlinear constrained optimiza- tion problem

For the purpose of simplifying our presentation,we next introduce some notations which will be used frequently throughout this paper.
Let

Further,we denote the set of active constraints at the point x ∈ D by

Now,we give the generalized Slater constraint qualification for constrained optimization problems with invex functions.
It is said that the generalized Slater constraint qualification is satisfied at <x ∈ D for the considered optimization problem (P) if there exists a feasible solution ex such that gi(ex) < 0 (i ∈ I(x)). Moreover,gi(i ∈ I(x))) are invex at x on D with respect to the same function η defined by η: D × D → Rn.
It is well-known (see,for example,Refs. [1] and [2]) that the following Karush-Kuhn-Tucker conditions are necessary for optimality of a feasible solution x for the considered nonlinear optimization problem.
Theorem 1 Let x be an optimal solution in Problem (P) and the generalized Slater con-straint qualification be satisfied at x. Then,there exist the Lagrange multipliers ξ ∈ Rm and μ ∈ Rs such that
In the present paper,we assume that some constraint qualification (for instance,the gen- eralized Slater constraint qualification mentioned above) is satisfied at any optimal solution in the considered optimization problem (P).
Definition 1 The point (x,ξ,μ) ∈ D×Rm×Rs is said to be a Karush-Kuhn-Tucker point in Problem (P) if the Karush-Kuhn-Tucker necessary optimality conditions (1)-(3) are satisfied at x with the Lagrange multipliersξ and μ.
Nonlinear programming has a wide range of applications in management science,economics, engineering,and other scientific branches. A considerable amount of investigation has been devoted to methods that attempt to solve nonlinear constrained optimization problems by means of a single minimization of an unconstrained optimization problem,for example,the exact penalty methods. In exact penalty function methods,as opposed to the classical sequential penalty methods (see,for example,Refs. [3],[4],and [5]),in which the original optimization problem is transformed into a sequence of unconstrained optimization problems,the original constrained optimization problem is replaced by an unconstrained optimization problem. In such an optimization problem,the objective function is the sum of a certain “merit” function (which reflects the objective function of the original problem) and a penalty term which reflects the constraint set. The merit function is chosen,in general,as the original objective function, while the penalty term is obtained by multiplying a suitable function,which represents the constraints,by a positive parameter c,called the penalty parameter. A given penalty parameter c is called an exact penalty parameter if every solution of the constrained extremum problem can be found by solving the unconstrained optimization problem with the penalty function associated with c.
The exact penalty functions have quite different features. One important property that distinguishes these functions is the exactness of the penalization. The concept of the exactpenalization is sometimes ambiguous or at least varies from author to author. One of the definitions of the exactness of the penalization is as follows: there is an appropriate penalty parameter choice such that a single unconstrained minimization of the penalty function yields a solution of the constrained optimization problem.
A particular class of the exact penalty function methods can be subdivided,in turn,into two main classes,i.e.,nondifferentiable exact penalty function methods and continuously dif- ferentiable exact penalty function methods. Nondifferentiable exact penalty functions were introduced for the first time by Zangwill[6] and Pietrzykowski[7].
The best known class of nondifferentiable penalty functions was defined by Han and Man- gasarian[8] as follows:
where c > 0,and ||·||p denotes the lp norm over Rm+s for 1 ≤ p ≤ ∞. For a given constraint gi(x) ≤ 0,the function g+i (x) defined by is equal to zero for all x that satisfy the constraint,and it has a positive value whenever this constraint is violated. Moreover,large violations in the constraint gi(x) ≤ 0 result in large values of g+i (x). Thus,the function g+i (x) has the penalty features relative to the single constraint gi(x) ≤ 0. The unconstrained optimization problem defined above is called the penalized optimization problem with the exact minimax penalty function.For p = 1,we get the most known exact nondifferentiable penalty function,which is called the exact l1 penalty function (also the absolute value penalty function). The exact l1 penalty function method,also called the absolute value penalty function method,is the most popular exact nondifferentiable penalty function method. Most of the literature on nondifferentiable exact penalty function methods for optimization problems is devoted to studying the exactness property just for this exact penalty function method (see,for example,Refs. [1] and [9]-[20]). In Ref. [13],Charalambous introduced a class of nondifferentiable exact penalty functions with nonnegative parameters for p > 1.
For p = ∞,we obtain the so-called exact minimax penalty function. The exact minimax penalty function method has been used by Bandler and Charalambous[21]. They formulated, for the given nonlinear optimization problem,an unconstrained minimax problem. Under reasonable restrictions,Bandler and Charalambous showed that a point satisfying the necessary conditions for a minimax optimum also satisfies the Kuhn-Tucker necessary conditions for the considered constrained optimization problem.
In the literature on exact penalty functions,in general,one of the most important issues is to give the conditions in order to ensure that the penalty function has a minimum at an optimal solution in the given constrained optimization problem (P) for all sufficiently large but finite c and to provide a lower bound on the critical penalty parameter. In the present paper,we use the exact minimax penalty function method to solve the general nonconvex differentiable optimization problem with both inequality and equality constraints. Therefore,for the considered constrained optimization problem (P),we construct an associated unconstrained optimization problem (P∞(c)),called a penalized optimization problem with the exact minimax penalty function. Then,we study the property of the exactness of the penalization for the exact minimax penalty function method. Thus,the main purpose of this paper is to relate an optimal solution in the considered constrained optimization problem (P) with a minimizer of its associated penalized optimization problem (P∞(c)) with the exact minimax penalty function. We prove that,for all penalty parameters c exceeding the given threshold,the set of all optimalsolutions in the given constrained optimization problem is equal to the set of all minimizers in its associated penalized optimization problem (P∞(c)) with the exact minimax penalty function. Further,we obtain a lower bound for the controlling parameter of the penalty function which is expressed in the function of the Karush-Kuhn-Tucker multipliers. In order to prove these results,we assume that the functions constituting the considered optimization problem are invex with respect to the same function η (exception with those equality constraints for which the associated Lagrange multipliers are negative—these functions are assumed to be incave also with respect to the same function η). We show that,if this assumption is omitted,then the equivalence between the sets of optimal solutions in Problem (P) and (P∞(c)) might not hold for all penalty parameters c exceeding this threshold. The results established in the paper are illustrated by suitable examples of constrained optimization problems solved by using the exact minimax penalty function method.
2 Basic notations and preliminary definitionsIn recent years,various generalizations of convex functions have been derived which proved to be useful for extending optimality conditions and some classical duality results,previously restricted to convex programs,to larger classes of optimization problems. One of them is the invexity notion introduced by Hanson[22]. He extended the concept of an convex function and applied the invexity notion to prove optimality conditions and duality results for nonconvex constrained optimization problems. Later,Craven[23] named those functions as invex functions.
Now,we recall the definition of an invex function introduced by Hanson[22].
Definition 2 Let X be a nonempty open subset of Rn and f : X → R be a differentiable function defined on X. If there exists a vector-valued function η : X × X → Rn such that the inequality
holds for all x ∈ X (x ≠ u),then f is said to be (strictly) invex at u ∈ X on X with respect to η. If (6) is satisfied for any u ∈ X,then f is an invex function on X with respect to η.Remark 1 In the case when η (x,u) = x − u,we obtain the definition of a differentiable convex function.
Definition 3 Let X be a nonempty open subset of Rn and f : X → R be a differentiable function defined on X. If there exists a vector-valued function η: X × X → Rn such that
holds for all x ∈ X (x 6= u),then f is said to be (strictly) incave at u ∈ X on X with respect to η. If (7) is satisfied for any u ∈ X,then f is an incave function on X with respect to η.Remark 2 In the case when η (x,u) = x − u,we obtain the definition of a differentiable concave function.
In order to prove the main results in the paper,we need a useful lemma whose simple proof is omitted in this work.
Lemma 1 Let φk (k = 1,2,· · · ,p) be real-valued functions defined on X ⊂ Rn. For eachx ∈ X,one has

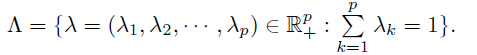
Now,for convenience,we also recall the definition of a coercive function (see Ref. [24]).
Definition 3 A continuous function f : Rn → R is said to be coercive if

This means that,for any constant M,there must be a positive number βM such that f(x) > M whenever ||x|| > βM. In particular,the values of f cannot remain bounded on a set X in Rn that is not bounded.
Remark 3 For f to be coercive,it is not sufficient that f(x) → ∞ as each coordinate tends to ∞. f must become infinite along any path for which ||x|| becomes infinite.
3 Exactness of minimax penalty function method for invex programming problemsIn the exact minimax penalty function method,for the given constrained extremum problem (P),we construct the following unconstrained optimization problem:
The idea of the exact minimax penalty function method is to solve the original nonlinear constrained optimization problem (P) by means of a single unconstrained minimization problem (P∞(c)). Roughly speaking,a minimax penalty function for Problem (P) is a function P∞(x,c)given by (4),where c > 0 is the penalty parameter, with the property that there exists a lowerbound c such that,for c > c,any optimal solution of Problem (P) is also a minimizer in the minimax penalized optimization problem (P∞(c)) with the exact minimax penalty function.
In this section,we give a new characterization of the exact minimax penalty function method used for solving the nonconvex differentiable optimization problem (P) with both inequality and equality constraints. Namely,we establish new conditions for characterization of one of the most important properties of this exact penalty function method,which is the exactness of the penalization.
We now show that,for a penalty parameter exceeding the given threshold,a Karush-Kuhn- Tucker point in the constrained optimization problem (P) yields a minimizer in its associated penalized optimization problem (P∞(c)) with the exact minimax penalty function.
Theorem 2 Let(x,ξ,μ) ∈ D × Rm × Rs be a Karush-Kuhn-Tucker point in the givenconstrained optimization problem (P). Let

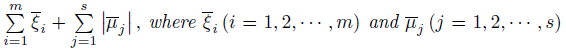 the Lagrange multipliers associated with the constraint functions gi and hj ,respectively),then
x is also a minimizer in the penalized optimization problem (P∞(c)) with the exact minimaxpenalty function
the Lagrange multipliers associated with the constraint functions gi and hj ,respectively),then
x is also a minimizer in the penalized optimization problem (P∞(c)) with the exact minimaxpenalty functionProof By assumption,the objective function f and the constraint functions gi (i ∈ I (x))and hj (j ∈ J+ (x)) are invex functions at x on X with respect to η. Moreover,the constraint function hj (j ∈ J− (x)) is incave at x on X with respect to η. Then,by Definitions 2 and 3, the inequalities
hold for all x ∈ X. Since ξi ≥ 0 (i ∈ I),μj > 0 (j ∈ J+(x)),and μj < 0 (j ∈ J−(x)),the inequalities (10)-(12) imply Taking into account the Lagrange multipliers equal to 0,we get Hence,the inequalities (15) and (16) yield,respectively, Now,adding both sides of (9),(17),and (18),we get




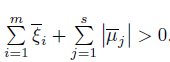 Thus,
We denote
Note that
Combining (20)-(24),we obtain that for all x ∈ X,
Thus,
We denote
Note that
Combining (20)-(24),we obtain that for all x ∈ X,




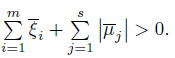 Thus,
Thus,




Using the Karush-Kuhn-Tucker necessary optimality condition (1) together with the in- equality (9),we get




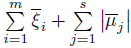 ,x is optimal in the penalized optimization problem (P∞(c))with the exact minimax penalty function. This completes the proof of the theorem.
,x is optimal in the penalized optimization problem (P∞(c))with the exact minimax penalty function. This completes the proof of the theorem.
Corollary 1 Let x be an optimal point in the considered constrained optimization problem
(P). Furthermore,assume that the objective function f and the constraint functions gi (i ∈ I (x))
and hj (j ∈ J+ (x)) are invex at x on X with respect to the same function η. Moreover,the
constraint function hj (j ∈ J− (x)) is incave at x on X with respect to η. If c is assumed
to be sufficiently large (it is sufficient to set c >
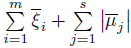 ,where ξi (i = 1,2,· · · ,m)
and μj(j = 1,2,· · · ,s) are the Lagrange multipliers associated to the constraints gi and hj ,
respectively,such that the Karush-Kuhn-Tucker necessary optimality conditions are satisfied
at x with these multipliers),then x is also a minimizer in the penalized optimization problem
(P∞(c)) with the exact minimax penalty function.
,where ξi (i = 1,2,· · · ,m)
and μj(j = 1,2,· · · ,s) are the Lagrange multipliers associated to the constraints gi and hj ,
respectively,such that the Karush-Kuhn-Tucker necessary optimality conditions are satisfied
at x with these multipliers),then x is also a minimizer in the penalized optimization problem
(P∞(c)) with the exact minimax penalty function.
Now,under the stronger invexity assumptions imposed on the functions constituting the given optimization problem (P),we prove the converse result. Thus,we show that there exists a threshold of the penalty parameter c,above which x,being a minimizer in the penalized optimization problem (P∞(c)) with the exact minimax penalty function,is also optimal in the considered nonconvex extremum problem (P).
Theorem 3 Let the point x be a minimizer in the penalized optimization problem (P∞(c))
with the exact minimax penalty function,and let the penalty parameter c be sufficiently large
(that is,c >
 ,where
,where  is a Karush-Kuhn-Tucker point in Problem (P)).
Furthermore,assume that the objective function f and the constraint functions gi (i ∈ I (
is a Karush-Kuhn-Tucker point in Problem (P)).
Furthermore,assume that the objective function f and the constraint functions gi (i ∈ I (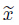 ))
and hj
))
and hj are invex at
are invex at 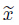 on X with respect to η. Moreover,the
constraint
on X with respect to η. Moreover,the
constraint  is incave at
is incave at 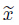 on X with respect to η. If the set
D of all feasible solutions in the given constrained optimization problem (P) is compact,then x
is also an optimal solution in Problem (P).
on X with respect to η. If the set
D of all feasible solutions in the given constrained optimization problem (P) is compact,then x
is also an optimal solution in Problem (P).
Proof Since x is optimal in the penalized optimization problem (P∞(c)) with the exact minimax penalty function,the inequality



Now,in order to prove that x is optimal in the considered optimization problem (P),we have to show that x is feasible in Problem (P). By means of contradiction,suppose that x i not feasible in Problem (P). Since f is a continuous function bounded below on the compact set D,by Weierstrass’ theorem,f admits its minimum 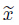 on D. Therefore,the given optimization problem (P) has an optimal solution
on D. Therefore,the given optimization problem (P) has an optimal solution 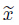 . Hence,the Karush-Kuhn-Tucker necessary optimality
conditions are satisfied at
. Hence,the Karush-Kuhn-Tucker necessary optimality
conditions are satisfied at 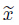 with the Lagrange multipliers
with the Lagrange multipliers  ∈ Rm
+ and
∈ Rm
+ and  ∈ Rs. By the
assumption,the objective function f and the constraint functions gi (i ∈ I (
∈ Rs. By the
assumption,the objective function f and the constraint functions gi (i ∈ I (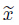 )) and hj (j ∈
J+ (
)) and hj (j ∈
J+ (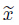 )) are inv
)) are inv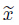 at
at 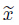 on X with respect to the same function η. Moreover,the constraint
function hj (j ∈ J− (
on X with respect to the same function η. Moreover,the constraint
function hj (j ∈ J− (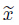 )) is incave at
)) is incave at 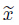 on X with respect to the same function η. Therefore,by Definitions 2 and 3,respectively,the following inequalities
on X with respect to the same function η. Therefore,by Definitions 2 and 3,respectively,the following inequalities

Since the Karush-Kuhn-Tucker necessary optimality conditions (1)-(3) are satisfied at ex
with the Lagrange multipliers  ∈ Rm
+ and
∈ Rm
+ and  ∈ Rs,the inequalities (32)-(34) imply that
∈ Rs,the inequalities (32)-(34) imply that


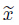 in Problem (P) and the Karush-Kuhn-Tucker necessary optimality
condition (2),it follows that
in Problem (P) and the Karush-Kuhn-Tucker necessary optimality
condition (2),it follows that


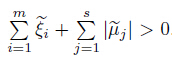 . Dividing the above inequality by
. Dividing the above inequality by
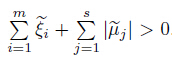 ,we get
We denote
Note that
Combining (37)-(42),we obtain
,we get
We denote
Note that
Combining (37)-(42),we obtain



In the case when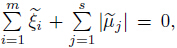 by the Karush-Kuhn-Tucker necessary optimality
conditions (1) and (31),it follows that
by the Karush-Kuhn-Tucker necessary optimality
conditions (1) and (31),it follows that

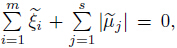 yields
yields


Thus,by the assumption  ,we have established that x is feasible in the
given extremum problem (P).
,we have established that x is feasible in the
given extremum problem (P).
Then,the optimality of x in the considered optimization problem (P) follows directly from the inequality (30). Hence,this completes the proof of the theorem.
The following result follows directly from Corollary 1 and Theorem 3.
Corollary 2 Let the hypotheses of Corollary 1 and Theorem 3 be satisfied. Then,the set of optimal solutions in the given constrained optimization problem (P) and the set of minimizers in its associated penalized optimization problem (P∞(c)) with the exact minimax penalty function coincide.
Now,we illustrate the results established in the paper by the example of a constrained optimization problem with invex functions. To solve it,we use the exact minimax penalty function method.
Example 1 Consider the following nonlinear optimization problem with both inequality and equality constraints:


on problem (P∞(c)) with the exact minimax penalty function given above. Conversely,since all hypotheses of Theorem 3 are also fulfilled,x = (0,0) is a minimizer in Problem (P∞(c)),where c > 2 is also optimal in the considered constrained optimization problem (P1).
In the next example,we consider a constrained optimization problem in which not all func- tions are invex. It turns out that,for such constrained optimization problems,the equivalence might not hold between the set of optimal solutions in the given optimization problem and the set of minimizers in its associated penalized optimization problem with the exact minimax penalty function.
Example 2 Consider the following constrained optimization problem:


In the next example,we consider a constrained optimization problem in which the objective function is coercive,but it is not an invex function. It turns out that,for such constrained op- timization problems,the equivalence might not hold between the set of optimal solutions in the given optimization problem and the set of minimizers in its associated penalized optimization problem with the exact minimax penalty function.
Example 3 Consider the following constrained optimization problem:


In the paper,the exact minimax penalty function method is used to solve nonconvex dif- ferentiable optimization problems involving both inequality and equality constraints. A new characterization of its exactness property is given in the case of solving such nonlinear con- strained extremum problems. In this method,for the considered differentiable optimization problem (P),an associated penalized optimization problem (P∞( c) with the exact minimax penalty function is constructed. A lower bound on the penalty parameter c has been given in the paper,and for all penalty parameters c exceeding this threshold,the sets of optimal solutions in both Problems (P) and (P∞( c) are the same. This result has been established under the assumption that the functions constituting the considered constrained optimization problem are invex with respect to the same function η (exception with those equality constraints for which the Lagrange multipliers are negative—these functions are assumed to be incave with respect to η). Further,it is shown that,in the case when the objective function is not invex, the equivalence between the set of optimal solutions in the constrained optimization problem (P) and the set of minimizers in its associated penalized optimization problem (P∞( c) with the exact minimax penalty function does not hold. It is also shown that the coercivity of the objective function is not the sufficient assumption in order to prove this equivalence for all penalty parameters exceeding this threshold if the objective function is not invex. Therefore, it has been shown that the concept of invexity is useful in order to characterize the property of exactness of the penalization for the exact minimax penalty function method. The principal motivation for this characterization of the exact minimax penalty function method presented in this paper is also that,in comparison to the classical exact l1 penalty function method,there is no lower bound on the penalty parameter c in the optimization literature such that,for any value of the penalty parameter above the threshold,the mentioned equivalence holds between such a class of nonconvex optimization problems and their associated penalized optimization problems with the exact minimax penalty function.
| [1] | Bazaraa, M. S., Sherali, H. D., and Shetty, C. M. Nonlinear Programming: Theory and Algorithms, John Wiley and Sons, New York (1991) |
| [2] | Mangasarian, O. L. Nonlinear Programming, McGraw-Hill, New York (1969) |
| [3] | Bertsekas, D. P. Constrained Optimization and Lagrange Multiplier Methods, Academic Press, New York (1982) |
| [4] | Fiacco, A. V. and McCormick, G. P. Nonlinear Programming: Sequential Unconstrained Mini-mization Techniques, John Wiley and Sons, New York (1968) |
| [5] | Fletcher, R. A class of methods for nonlinear programming with termination and convergence properties. Integer and Nonlinear Programming (ed. Abadie, J.), North-Holland Publishing, Am-sterdam, 157-173 (1970) |
| [6] | Zangwill, W. I. Nonlinear programming via penalty functions. Management Science, 13, 344-358 (1967) |
| [7] | Pietrzykowski, T. An exact potential method for constrained maxima. SIAM Journal of Numerical Analysis, 6, 294-304 (1969) |
| [8] | Han, S. P. and Mangasarian, O. L. Exact penalty functions in nonlinear programming. Mathe-matical Programming, 17, 251-269 (1979) |
| [9] | Antczak, T. Exact penalty functions method for mathematical programming problems involving invex functions. European Journal of Operational Research, 198, 29-36 (2009) |
| [10] | Antczak, T. The l1 penalty function method for nonconvex differentiable optimization problems with inequality constraints. Asia-Pacific Journal of Operational Research, 27, 1-18 (2010) |
| [11] | Antczak, T. A new exact exponential penalty function method and nonconvex mathematical programming. Applied Mathematics and Computation, 217, 6652-6662 (2011) |
| [12] | Bertsekas, D. P. and Koksal, A. E. Enhanced optimality conditions and exact penalty functions. Proceedings of Allerton Conference, Allerton, lllinois (2000) |
| [13] | Charalambous, C. A lower bound for the controlling parameters of the exact penalty functions. Mathematical Programming, 15, 278-290 (1978) |
| [14] | Evans, J. P., Gould, F. J., and Tolle, J. W. Exact penalty functions in nonlinear programming. Mathematical Programming, 4, 72-97 (1973) |
| [15] | Fletcher, R. An exact penalty function for nonlinear programming with inequalities. Mathematical Programming, 5, 129-150 (1973) |
| [16] | Luenberger, D. Control problem with kinks. IEEE Transaction on Automatic Control, 15, 570-574 (1970) |
| [17] | Mangasarian, O. L. Sufficiency of exact penalty minimization. SIAM Journal of Control and Optimization, 23, 30-37 (1985) |
| [18] | Di Pillo, G. and Grippo, L. A continuously differentiable exact penalty function for nonlinear programming problems with inequality constraints. SIAM Journal of Control and Optimization, 23, 72-84 (1985) |
| [19] | Di Pillo, G. and Grippo, L. Exact penalty functions in constrained optimization. SIAM Journal of Control and Optimization, 27, 1333-1360 (1989) |
| [20] | Rosenberg, E. Exact penalty functions and stablility in locally Lipschitz programming. Mathema-tical Programming, 30, 340-356 (1984) |
| [21] | Bandler, J. W. and Charalambous, C. Nonlinear programming using minimax techniques. Journal of Optimization, Theory and Applications, 13, 607-619 (1974) |
| [22] | Hanson, M. A. On sufficiency of the Kuhn-Tucker conditions. Journal of Mathematical Analysis and Applications, 80, 545-550 (1981) |
| [23] | Craven, B. D. Invex functions and constrained local minima. Bulletin of the Australian Mathe-matical Society, 24, 357-366 (1981) |
| [24] | Peressini, A. L., Sullivan, F. E., and Uhl, J. J., Jr. The Mathematics of Nonlinear Programming, Springer-Verlag, New York (1988) |
| [25] | Ben-Israel, A. and Mond, B. What is invexity? Journal of Australian Mathematical Society Series B, 28, 1-9 (1986) |
 2015, Vol. 36
2015, Vol. 36













































