Shanghai University
Article Information
- Zailin YANG, Baoping HEI, Yao WANG. 2015.
- Scattering by circular cavity in radially inhomogeneous medium with wave velocity variation
- Appl. Math. Mech. -Engl. Ed., 36(5): 599-608
- http://dx.doi.org/10.1007/s10483-015-1937-7
Article History
- Received 2014-08-21;
- in final form 2014-10-15
The problem of elastodynamics for inhomogeneous medium is of great interest in the wave motion field. On the basis of complicated mathematical derivations,a great number of works have appeared,with the inhomogeneity of medium varing continuously along one-dimensional direction only,i.e.,the depth-dependent variation,axial symmetric variation,and radial variation according to an exponential or a power law. Axially symmetric problems of inhomogeneous medium have attracted growing attention in recent years due to their wide applications in many fields such as electromagnetism,acoustics,and elastic mechanics. Meanwhile,axially symmetric problems are typical cases for inhomogeneous hollow cylinder,circular functionally graded material (FGM) disk,circular tube with inhomogeneous coating,infinite plate with a circular hole,etc.
Axially symmetric problems of inhomogeneous medium in electromagnetic field were studied by Van and Wood[1] by using the time-domain finite element method. The static Maxwell system with an axially symmetric dielectric permittivity and complete systems of its solution was constructed in Ref. [2]. Additionally,for acoustic propagation,a polynomial approach[3, 4] was adopted to discuss guided waves in an inhomogeneous elastic body with the material properties varying in the direction of the thickness according to a known radial variation law. Baron[5] studied the influence of a tubular waveguide on the propagation of elastic waves in an anisotropic hollow cylinder with elastic properties (stiffness coefficients and mass density) continuously varying in the radial direction. While the density and shear modulus vary exponentially along the x-direction in the same form,the dynamic stress concentration by the anti-plane SH waves around the circular cavity in a semi-infinite FGM was investigated by Fang et al[6]. The same method was extended to study the scattering problems by a cylindrical inclusion in the functionally graded or piezoelectric materials[7, 8]. Furthermore,the boundary element method (BEM) was an efficient numerical method to study the anti-plane dynamic analysis around the hole and crack under SH waves in the functionally graded piezoelectric medium[9],which was first developed by Monalis[10] for the problems of scattering of elastic waves by circular cavities in inhomogeneous elastic medium. The analogous problems for radially inhomogeneous medium are part of what is known to deal with elastic mechanic problems. Greif and Chou[11] investigated the transient response of a thick-walled cylinder or plate subjected to an axially symmetric time-dependent pressure at an internal or external surface. Rvachev et al.[12] evaluated axially symmetric problem of elasticity theory for an inhomogeneous cylinder by employing the R-functions in order to find approximate solutions for inhomogeneous finite bodies. Wang and Gong[13] obtained a theoretical solution for the basic equation of axisymmetric problems in elastodynamics,which satisfies inhomogeneous boundary conditions. An axially symmetric contact problem of pressing an absolutely rigid ball into an inhomogeneous half space formed by a homogeneous base and an inhomogeneous surface layer was presented in Ref. [14]. Tarn and Chang[15] studied the torsion of elastic circular bars of radially inhomogeneous,cylindrically orthotropic materials. When shear modulus and the wave speed were different in radial and regular directions,Boström et al.[16] considered the propagation of horizontally polarized shear waves in a radially inhomogeneous anisotropic medium under a point source or a plane wave.
The radial stress distribution for axisymmetric problems around the inhomogeneous cylinder, where the medium properties vary in the radial direction,has been received considerable attention in recent years. For exponential or power law Young’s modulus and constant Poisson’s ratio,the plane axisymmetric problem for a radially inhomogeneous circular was analyzed in Ref. [17]. When Young’s modulus varies in the radial direction with power law and Poisson’s ratio was constant,Sburlati[18] presented the stress concentration factor around an inhomogeneous annular ring made of FGM in an isotropic homogeneous plate. By assuming that material properties (including the mechanical and electrical properties) vary in the thickness direction, an analytical-numerical method was presented by Han and Liu[19] for analyzing dispersion and characteristic surface of waves in a circular cylinder made of functionally graded piezoelectric material. Considering the power law variation of elastic and viscoelastic parameters,Acharya et al.[20] investigated radial displacement and relevant stress components in inhomogeneous, isotropic and viscoelastic medium.
Recently,interests on stress concentration analysis around circular cavity in graded functionally material varying radially have significantly increased. With regard to a functional graded material plate with a circular cavity,Zhang et al.[21] provided an exact thermal stress solution for the material properties and applied temperature varying arbitrarily in the radial direction. Afsar and Go[22] studied the thermoelastic field in a thin circular FGM disk with material properties exponentially varying in radial direction only by using the finite element method. Kubair and Bhanu-Chandar[23] investigated the effect of the material property inhomogeneity on the stress concentration factor due to a circular hole in functionally graded panels. Mohammadi et al.[24] discussed the stress concentration factor around a hole subjected to the uniform biaxial tension and pure shear. There was a constrain condition that both Yong’s modulus and Passion’s ratio were exceptional functions. In case of variation of radial arbitrary elastic properties, Yang et al.[25, 26] investigated the two-dimensional (dynamic) stress distribution around a circular hole under arbitrary loads by using the method of piece-wise homogeneous layers.
This paper aims to present an analytical solution for the dynamic stress concentration around a circular cavity in a radially inhomogeneous medium. Here,the inhomogeneity of medium is reflected by the variable wave number which varies along the radial direction with a power law variation and the shear modulus is constant. Based on the homogenization principle,the Helmholtz equation with a variable coefficient can be converted to the standard Helmholtz equation by using the general conformal transformation method (GCTM). The dynamic displacement and stress fields are determined in the complex coordinate systems by using the complex function method[27]. Numerical results are given to discuss the effects of wave number and inhomogeneity parameter of medium on the dynamic stress distribution around the circular cavity. 2 Description of inhomogeneity
An infinite inhomogeneous medium with a circular cavity of radius a is shown in Fig. 1. The origin of the polar coordinate system is assumed to be located at the center of the cavity. The elastic medium is inhomogeneous and isotropic. The inhomogeneity of medium varies continuously in the radial direction and approaches uniform values at distance far away from the circular cavity and the shear modulus is constant. The time harmonic elastic waves propagate with the incident angle α in radially inhomogeneous medium. According to a power law,the variable wave velocity is assumed as
 |
| Fig. 1 Model of radially inhomogeneous elastic medium with circular cavity |
where c0 is the reference wave velocity,and β is the inhomogeneity parameter of medium which stands for the spatial variation of velocity in the radially inhomogeneous medium. 3 Governing equation
By supposing harmonic response and neglecting body force,the governing equation for elastic waves problem is a Helmholtz equation with a variable coefficient
where x = (x,y) is the position vector,∇2 is the Laplacian,k = ω/c,c =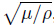 ,k is the wave
number,ω is the circular frequency of the displacement φ,c is the shear wave velocity,and ρ
and μ are the mass density and the shear modulus of the inhomogeneous medium,respectively.
,k is the wave
number,ω is the circular frequency of the displacement φ,c is the shear wave velocity,and ρ
and μ are the mass density and the shear modulus of the inhomogeneous medium,respectively.
(2) written in the cylindrical coordinates system (r,θ,z),where the z-axis is the axis of the cylindrical cavity,takes the form
In this work,we focus on a two-dimensional Helmholtz equation with the condition of axial symmetry of the velocity about the z-axis. On the base of the relation between k and c,(1) can be expressed as follows:
where k0 = ω/c0 is the reference wave number. Thus,(3) can be written as By introducing the complex variable system z = reiθ,(5) becomesIn order to homogenize the Helmholtz equation with variable coefficient,the conformal transformation relation is introduced,
Substituting (7) into (6) yields the governing equation Note that the above equation corresponds to the standard the Helmholtz equation in the mapping plane. 4 Displacement fields and boundary condition 4.1 Forms of displacement fieldsAccording to (8),the general solution of the scattered fields resulting from a circular cavity in an inhomogeneous infinite medium can be written as follows:
In the complex coordinate system (z,z),the form of scattering wave can be expressed as where An are undetermined coefficients,and Hn(1)(·) is the first kind Hankel function of the nth order.Due to the axially symmetry of the problem,we consider the case that α = 0 only. In the complex coordinate system (ζζ,ζ),the form of incident wave can be given by
where φ0 is the amplitude of incident wave.We note that (11),as an expression of incident waves,satisfies the transformed the Helmholtz equation (e.g.,(8)). The amplitude of φ(i) in inhomogeneous medium is equal to the reference amplitude φ0,while the phase angle is different from that in reference homogeneous medium due to the conformal transformation,which reflects the inhomogeneity of medium.
The whole wave field in an inhomogeneous infinite medium is the superposition of the incident wave and the scattering wave,which can be written as
4.2 Expressions of stress componentsIn cylindrical coordinate systems (r,θ,z),the constitutive relations between stress components and the displacement are shown to be
In complex coordinate systems (z,z),the corresponding stress components can be expressed as Similarly,in the complex plane ζ,(14) and (15) can be written as By substituting (11) into (14) and (15),the stress components of incident wave are Substitution of (9) into (16) and (17) leads to the stress components of scattering wave 4.3 Boundary conditionWithout loss of generality,the case that the circular cavity is free of traction is investigated. The boundary condition is that the radial shear stress is equal to zero,i.e.,
Substituting (18) and (20) into (22) yields where Multiplying both sides of (23) with e−imθ and integrating on the interval (−π,π),we find An defined infinity algebraic equation set as follows: where 5 Dynamic stress concentration factor (DSCF)In this paper,the DSCF is defined as the ratio of the stress τθz (induced by total displacement field) to the stress ττ0 (induced by incident wave). For elastic waves,the DSCF is given by
where Substituting (19) and (21) into (28) yields the final expression as follows: 6 Numerical results and discussionIn order to highlight the capability of the present approach for dynamic stress concentration around a circular cavity in the radially inhomogeneous medium,the numerical calculations are provided by truncating the set of infinite algebraic equations. Obviously,the accuracy of the numerical results is dependent on the choice of n. Here,we truncate the infinite matrix to n = 9,where the accuracy can reach 10−18. Meanwhile,the following dimensionless variables are adopted: the reference wave number is k0a,and the inhomogeneity parameter of medium is βa. The distributions of the DSCF around the circular cavity in radially inhomogeneous medium are shown in Figs. 2-5 for different inhomogeneity parameter of medium βa = 0.1,0.2,0.3,and 0.4. It shows that the maximum of the DSCF is at θ = π when inhomogeneity parameter of medium tends to zero and the hoop stress distributions are symmetric with respect to the x-axis. As inhomogeneity parameter of medium increases,the maximum of the DSCF gets close to θ = ±π/2 except the case that dimensionless wave number k0a = 2. It is interesting that the fluctuation of the DSCF appears with the inhomogeneity parameter of medium βa increasing in the illumination region.
 |
| Fig. 2 Distribution of DSCF around circular cavity with inhomogeneity parameter of medium (βa=0.1) |
 |
| Fig. 3 Distribution of DSCF around circular cavity with inhomogeneity parameter of medium (βa=0.2) |
 |
| Fig. 4 Distribution of DSCF around circular cavity with inhomogeneity parameter of medium (βa=0.3) |
 |
| Fig. 5 Distribution of DSCF around circular cavity with inhomogeneity parameter of medium (βa=0.4) |
Figure 6 indicates the distribution of the DSCF around the circular cavity in radially inhomogeneous medium with inhomogeneity parameter of medium βa = 0.5,which corresponds to the case of homogeneous reference medium. The numerical results agree with the results of Pao and Mow[28] perfectly.
 |
| Fig. 6 Distribution of DSCF around circular cavity with inhomogeneity parameter of medium (βa=0.5) |
As mentioned in Figs. 7-9,the distributions of the DSCF around the circular cavity in radially inhomogeneous medium with inhomogeneity parameter of medium βa = 0.6,0.7,and 0.8 are described. As expected,the hoop stress distributions are symmetric with respect to the x-axis. The DSCF increases with reference wave number k0a increasing and the increasing degree of the DSCF at the position 2π/3 < θ < 4π/3 is more evident than that at the position −π/2 < θ < π/2. It is interesting to note that the fluctuation of the DSCF appears with the inhomogeneity parameter of medium βa increasing in the illumination region.
 |
| Fig. 7 Distribution of DSCF around circular cavity with inhomogeneity parameter of medium (βa=0.6) |
 |
| Fig. 8 Distribution of DSCF around circular cavity with inhomogeneity parameter of medium (βa=0.7) |
 |
| Fig. 9 Distribution of DSCF around circular cavity with inhomogeneity parameter of medium (βa=0.8) |
Figure 10 demonstrates the DSCFs versus inhomogeneity parameter of medium at θ = π/2. The distribution of the DSCF achieves the maximum when inhomogeneity parameter of medium βa = 0.65. It is interesting that the fluctuation of the DSCF appears sequentially for different k0a with βa increasing. Note that the greater the reference wave number is,the more evident the fluctuation is.
 |
| Fig. 10 DSCFs versus inhomogeneity parameter of media (θ = π/2) |
Analogously,Fig. 11 shows the DSCFs versus dimensionless wave number at θ = π/2. The fluctuation of the DSCF is evident while inhomogeneity parameter of medium vary in the range 0 < βa < 0.5. On the contrary,the fluctuation of the DSCF is slight for 0.5 < βa < 0.8. It is interesting to note that for inhomogeneity parameter of medium βa = 0.8,the fluctuation trend of the DSCF is similar to the case of βa = 0.5 corresponding to the homogeneous reference medium.
 |
| Fig. 11 DSCFs versus dimensionless wave numbers (θ = π/2) |
Based on the complex function theory,the present paper evaluates the dynamic stress concentration around a circular cavity in a radially inhomogeneous medium subjected to elastic wave by using the GCTM. The medium is assumed to have power variation of inhomogeneity in radial direction only and the shear modulus is constant. According to the homogenization principle, the Helmholtz equation with a variable coefficient is reduced into the standard Helmholtz equation. The general solutions of the scattering field are obtained and the dynamic stress distribution induced by a circular cavity is discussed. The numerical results reveal that inhomogeneity parameter of medium and wave number have great influence on the DSCF around the circular cavity. Thus,the wave fields in radially inhomogeneous medium can be controlled and optimized by controlling these parameters.
| [1] | Van, T. and Wood, A. A time-domain finite element method for Helmholtz equations. Journal of Computational Physics, 183(2), 486-507 (2002) |
| [2] | Khmelnytskaya, K. V., Kravchenko, V. V., and Oviedo, H. On the solution of the static Maxwell system in axially symmetric inhomogeneous media. Mathematical Methods in the Applied Sciences, 33(4), 439-447 (2010) |
| [3] | Elmaimouni, L., Lefebvre, J. E., Zhang, V., and Gryba, T. Guided waves in radially graded cylinders: a polynomial approach. NDT & E International, 38(5), 344-353 (2005) |
| [4] | Elmaimouni, L., Lefebvre, J. E., Raherison, A., and Ratolojanahary, F. E. Acoustical guided waves in inhomogeneous cylindrical materials. Ferroelectrics, 372(1), 115-123 (2008) |
| [5] | Baron, C. Propagation of elastic waves in an anisotropic functionally graded hollow cylinder in vacuum. Ultrasonics, 51(2), 123-130 (2011) |
| [6] | Fang, X. Q., Hu, C., and Du, S. Y. Strain energy density of a circular cavity buried in semiinfinite functionally graded materials subjected to shear waves. Theoretical and Applied Fracture Mechanics, 46(2), 166-174 (2006) |
| [7] | Fang, X. Q., Liu, J. X., Wang, X. H., Zhang, T., and Zhang, S. Dynamic stress from a cylindrical inclusion buried in a functionally graded piezoelectric material layer under electro-elastic waves. Composites Science and Technology, 69(7-8), 1115-1123 (2009) |
| [8] | Fang, X. Q., Liu, J. X., Zhang, L. L., and Kong, Y. P. Dynamic stress from a subsurface cylindrical inclusion in a functionally graded material layer under anti-plane shear waves. Materials and Structures, 44, 67-75 (2011) |
| [9] | Müller, R., Dineva, P., Rangelov, T., and Gross, D. Anti-plane dynamic hole-crack interaction in a functionally graded piezoelectric media. Archive of Applied Mechanics, 82(1), 97-110 (2012) |
| [10] | Manolis, G. D. Elastic wave scattering around cavities in inhomogeneous continua by the BEM. Journal of Sound and Vibration, 266(2), 281-305 (2003) |
| [11] | Greif, R. and Chou, S. C. The propagation of radially symmetric stress waves in anisotropic nonhomogeneous elastic media. Journal of Applied Mechanics, 38(1), 51-57 (1971) |
| [12] | Rvachev, V. L., Sinekop, N. S., and Kravchenko, L. K. Axially symmetric problem of elasticity theory for an inhomogeneous cylinder. International Applied Mechanics, 22(1), 11-16 (1986) |
| [13] | Wang, X. and Gong, Y. N. Theoretical solution for axially symmetric problems in elastodynamics. Acta Mechanica Sinica, 7(3), 275-282 (1991) |
| [14] | Kul'chyts'kyi-Zhyhailo, R. and Rogowski, G. Axially symmetric contact problem of pressing of an absolutely rigid ball into an elastic half space with inhomogeneous coating. Materials Science, 45(6), 845-858 (2009) |
| [15] | Tarn, J. Q. and Chang, H. H. Torsion of cylindrically orthotropic elastic circular bars with radial inhomogeneity: some exact solutions and end effects. International Journal of Solids and Structures, 45(1), 303-319 (2008) |
| [16] | Boström, A., Johansson, M., and Svedberg, T. Elastic wave propagation in a radially anisotropic medium. Geophysical Journal International, 118(2), 401-410 (1994) |
| [17] | Theotokoglou, E. E. and Stampouloglou, I. H. The radially nonhomogeneous elastic axisymmentric problem. International Journal of Solids and Structures, 45(25), 6535-6552 (2008) |
| [18] | Sburlati, R. Stress concentration factor due to a functionally graded ring around a hole in an isotropic plate. International Journal of Solids and Structures, 50(22-23), 3649-3658 (2013) |
| [19] | Han, X. and Liu, G. R. Elastic waves in a functionally graded piezoelectric cylinder. Smart Materials and Structures, 12(6), 962-971 (2003) |
| [20] | Acharya, D. P., Roy, I., and Biswas, P. K. Vibration of an infinite inhomogeneous transversely isotropic viscoelastic medium with cylindrical hole. Applied Mathematics and Mechanics (English Edition), 29(3), 367-378 (2008) DOI 10.1007/s10483-008-0308-z |
| [21] | Zhang, X. Z., Kitipornchai, S., Liew, K. M., Lim, C. W., and Peng, L. X. Thermal stresses around a circular hole in a functionally graded plate. Journal of Thermal Stresses, 26(4), 379-390 (2003) |
| [22] | Afsar, A. M. and Go, J. Finite element analysis of thermoelastic field in a rotating FGM circular disk. Applied Mathematical Modelling, 34(11), 3309-3320 (2010) |
| [23] | Kubair, D. V. and Bhanu-Chandar, B. Stress concentration factor due to a circular hole in functionally graded panels under uniaxial tension. International Journal of Mechanical Sciences, 50(4), 732-742 (2008) |
| [24] | Mohammadi, M., Dryden, J. R., and Jiang, L. Stress concentration around a hole in a radially inhomogeneous plate. International Journal of Solids and Structures, 48(3), 483-491 (2011) |
| [25] | Yang, Q., Gao, C. F., and Chen, W. Stress analysis of a functional graded material plate with a circular hole. Archive of Applied Mechanics, 80(8), 895-907 (2010) |
| [26] | Yang, Q. and Gao, C. F. Dynamic stress analysis of a functionally graded material plate with a circular hole. Meccanica, 48(1), 91-101 (2013) |
| [27] | Liu, D. K., Gai, B. Z., and Tao, G. Y. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion, 4(3), 293-304 (1982) |
| [28] | Pao, Y. H. and Mow, C. C. Diffraction of Elastic Waves and Dynamic Stress Concentrations, Crane and Russak, New York (1973) |
 2015, Vol. 36
2015, Vol. 36
































