Shanghai University
Article Information
- Xu HUANG, Ye YAN, Yang ZHOU, Hua ZHANG. 2015.
- Pseudospectral method for optimal propellantless rendezvous using geomagnetic Lorentz force
- Appl. Math. Mech. -Engl. Ed., 36(5): 609-618
- http://dx.doi.org/10.1007/s10483-015-1936-7
Article History
- Received 2014-06-16;
- in final form 2014-11-15
2. Department of Communication, Beijing Aerospace Control Center, Beijing 100094, China
Traditional spacecraft are generally propelled by thrusters using chemical fuels. The durations of most space missions are therefore constrained by the amount of propellant on board. To extend the orbital lifetime of the spacecraft,propellantless means of orbital control would be preferable. A Lorentz spacecraft is an artificially charged spacecraft that could modulate the surface charge to induce Lorentz force as it travels through the planetary magnetic field. This induced Lorentz force can be utilized as propellantless maneuvers to perform orbital control. Despite the restriction that the Lorentz force could only act in the direction perpendicular to the local magnetic field and the velocity of the spacecraft relative to the local magnetic field,the application of Lorentz force in space missions is still promising. Actually,various applications of Lorentz force as propellantless propulsion for orbital control have been proposed,including drag compensation[1],orbital inclination control[2],propellantless rendezvous[3, 4, 5],spacecraft hovering[6, 7],formation flying[8, 9, 10] and so on.
As to the research on the relative motion of Lorentz spacecraft,Pollock et al.[3] derived approximate analytical solutions to the orbital motion of Lorentz spacecraft with respect to near-circular reference orbit based on the Hill-Clohessy-Wiltshire equations. A propellantless rendezvous strategy is designed using the linearized relative dynamics model. In this strategy, restrictions are imposed on the initial relative states so that the Lorentz spacecraft nearly flies in the same circular equatorial orbit of the target spacecraft,initially lagging or leading the target spacecraft by some distance in the in-track direction with zero relative velocity. Then, maintaining a constant specific charge could achieve rendezvous with corresponding maneuver duration. Besides,the maneuver duration should equal an integer number of reference orbit periods and an integer number of rotation periods of the Earth to allow the relative distances in the radial direction and normal direction to return to zero. Yamakawa et al.[4] developed linearized dynamical models that describe the relative motion of Lorentz spacecraft in the vicinity of both circular and elliptic reference orbit by assuming that the Earth’s magnetic field can be modeled as a nontilted magnetic dipole aligned with true north. Likewise,strategies for in-plane rendezvous in equatorial orbits are designed. However,the Earth’s magnetic dipole is tilted by nearly 11.3◦ with respect to the rotation axis of the Earth,which is not sufficiently small to be negligible especially for inclined orbits. Thus,present linearized models may be less precise when applied in inclined Earth orbit.
Modeling the Earth’s magnetic field as a perfect tilted dipole located at the center of the Earth that co-rotates with Earth,a dynamical model that characterizes the relative motion of Lorentz spacecraft in the vicinity of arbitrary reference orbit is derived. Based on the proposed nonlinear dynamical model,this paper investigates the feasibility of only using Lorentz force as propulsion for rendezvous in inclined Earth orbit with no aforementioned restrictions on the initial relative states as those of previous work,aiming to develop the optimal trajectory that minimizes the required control energy for rendezvous. The resulting optimal control problem is then solved by a direct transcription method called Gauss pseudospectral method (GPM). Pseudospectral method has been widely applied in trajectory optimization problem in aerospace engineering. For example,Wu et al.[11] developed fuel-optimal low-thrust trajectories for spacecraft formation using Legendre pesudospectral method (LPM). Huntington and Rao[12] solved the optimal reconfiguration problem of spacecraft formations by GPM.
The remainder of this paper is organized as follows. First,the nonlinear dynamical model that describes the relative motion of Lorentz spacecraft is introduced in Section 2. Then,the propellantless rendezvous trajectory optimization problem is formulated in Section 3,followed by a brief review of GPM in Section 4. Classic examples are numerically simulated in Section 5 to demonstrate the validity of the proposed method. Section 6 gives the conclusions and future research work. 2 Dynamical model 2.1 Equations of relative motion
Consider two spacecrafts subject to the gravity field of the Earth,which are referred to as the chaser and target,respectively. The chaser is a charged Lorentz spacecraft whereas the target is uncharged. To describe the relative motion between the chaser and the target,several relevant coordinate frames are defined below,as shown in Fig. 1. OEXIYIZI is an Earth-centered inertial (ECI) frame located at the center of the Earth,OE. OTxyz is the relative motion (RM) frame fixed at the center of mass of the target,where x is along the radial direction,z is normal to the target’s orbital plane,and y completes the Cartesian right-handed frame. OL is the center of mass of the Lorentz spacecraft.
 |
| Fig. 1 Definition of reference frames |
Modeling the Lorentz spacecraft as point mass,the orbital motion equation of Lorentz spacecraft is given by
where RL is the orbital radius vector of the Lorentz spacecraft. aL = [ax ay az]T refers to the Lorentz acceleration experienced by the Lorentz spacecraft. μ is the gravitational parameter of the Earth.The position of the chaser with respect to the target is defined by ρ = [x y z]T. Therefore, the equations of orbital motion for the target and the nonlinear translational dynamics of the chaser with respect to the target can be written in the RM frame as follows[13]:
where RT is the orbital radius of the target,and RL = ((RT + x)2 + y2 + z2)1/2. uT is the argument of latitude of the target spacecraft. 2.2 Lorentz forceA charged particle is subject to the Lorentz acceleration as moving through a magnetic field, given by
where q is the charge,and m is the mass of the particle,and thus,q/m refers to the specific charge of the particle (i.e.,charge-to-mass ratio). Vr represents the velocity of the particle with respect to the local magnetic field B.To derive the expressions of Lorentz acceleration acting on the Lorentz spacecraft in the RM frame,following assumptions are imposed throughout this study: (i) the Earth’s magnetic field can be modeled as a perfect magnetic dipole located at the center of the Earth that co-rotates with Earth; (ii) the magnetic dipole is tilted by angle α with respect to the rotation axis of the Earth,as shown in Fig. 2.
 |
| Fig. 2 Definition of angles |
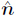 is a unit vector in the direction of the
magnetic dipole moment,given by
or in the RM coordinates,
where iT is the orbital inclination of the target spacecraft. The angle β is defined by β = ΩM−Ω,
where Ω refers to the right ascension of the ascending node of the reference orbit,and ΩM is
defined as
where ωE is the angular rotation rate of the Earth,and Ω0 is the initial phase angle of the
magnetic dipole.
is a unit vector in the direction of the
magnetic dipole moment,given by
or in the RM coordinates,
where iT is the orbital inclination of the target spacecraft. The angle β is defined by β = ΩM−Ω,
where Ω refers to the right ascension of the ascending node of the reference orbit,and ΩM is
defined as
where ωE is the angular rotation rate of the Earth,and Ω0 is the initial phase angle of the
magnetic dipole.
 L refers to the unit orbital radius vector of the Lorentz spacecraft,which can be expressed
in the RM frame as
L refers to the unit orbital radius vector of the Lorentz spacecraft,which can be expressed
in the RM frame as
Substitution of (7) and (9) into (5) yields the local magnetic field of the Lorentz spacecraft expressed in the RM frame.
The velocity of the Lorentz spacecraft with respect to the magnetic field is
where V refers to the absolute velocity of Lorentz spacecraft,given by Thus,the relative velocity Vr can be expressed in the RM frame asSubstitution of (5) and (12) into (4) yields the expressions of Lorentz acceleration in the RM frame,
The nonlinear relative translational dynamics of the Lorentz spacecraft is thus obtained by substituting (13) into (3). 3 Problem formulationTrajectory optimization can generally be defined as finding the optimal control profile of a dynamical system subject to several constraints that minimizes given objective functional. The propellantless rendezvous trajectory optimization problem can be formulated as follows.
Denote the specific charge of Lorentz spacecraft λ = q/m as the single control input. Determine the charge time (i.e.,maneuver time) and profile of specific charge to minimize an energy-optimal objective function,given by
The dynamic constraints of this optimization problem are presented in (2) and (3). Other constrains,including boundary constraints and path constraints,are summarized in the following subsections. 3.1 Boundary constraint
Boundary constraints for this problem contain initial state constraints and final state constraints. The initial state constraints are the initial states of the chaser with respect to the target,given by
To achieve rendezvous,it is required that both vehicles reach the same state at the final time. Thus,the final state constraints can be written as
3.2 Path constraint As presented in Ref. [1] by Peck,a specific charge of 0.03 C/kg seems to be the maximum that could be achievable in the near-term future. Hence,the path constraint on the specific charge is given by 4 GPMThe pseudospectral method,as a kind of direct method for trajectory optimization problem, transcribes the optimal control problem to nonlinear programming problem (NLP) by parameterizing state and control variables using global orthogonal polynomials and approximating dynamics at Gauss quadrature collocation points. In the GPM,Legendre polynomial and Legendre-Gauss (LG) points are used[14]. The resulting NLP is then solved by appropriate numerical methods. Detailed descriptions and comparisons of different kinds of pesudospectral methods can be found in Refs. [15]-[21]. The GPM is adopted in this paper. 5 Numerical simulation 5.1 Scenario 1
In this subsection,two examples are simulated to testify the validity of pesudospectral method in solving the aforementioned trajectory optimization problem. Both examples are solved by utilizing the open source code package called GPOPS [22] and the NLP solver SNOPT [23] using default optimality and feasibility tolerance. The target spacecraft is assumed to be flying in a near-circular inclined low Earth orbit with an orbital period of 1.6 hour. The initial orbital elements of the target spacecraft are given in Table 1. The initial phase angle of the magnetic dipole Ω0 is set as 40◦. In the first example,the final time tf is fixed whereas it is free in the second example. In both examples,the number of LG points is 50 and the initial boundary constrains are chosen as
The final time is fixed at tf5 000 s. Figure 3 shows the time history of specific charge,from which it is clear that the specific charge is on the order of 10−3 and is less than the maximum 0.03 C/kg. The solid line in Fig. 3 is the result of the Lagrange polynomial interpolation of the specific charges at the LG points and the cost function is J = 5.74 × 10−3. Figures 4 and 5 show,respectively,the time histories of relative position and relative velocity. To prove the validity of the results derived by GPM,the interpolated trajectory of specific charge is then substituted into the nonlinear dynamical model and the actual trajectory is generated by integrating the nonlinear equations ((2) and (3)) using the 4th order Runge-Kutta method,as shown by the solid lines in Figs. 4 and 5. It can be seen that the relative states obtained from numerical integration nearly coincide with the results derived via the GPM,and propellantless rendezvous is achieved at the given final time. The terminal relative position errors in the radial,in-track,and normal direction are,respectively,0.52 m,0.43 m,and 0.008 m. The terminal relative velocity errors in each component are 1.15 × 10−4 m/s,1.10 × 10−3 m/s,and 5.20 × 10−6 m/s. Using more LG points can further reduce these errors. These errors partly result from the interpolation of the specific charge and the numerical integration method,which will be analyzed in the future research.
 |
| Fig. 3 Time history of specific charge (tf5 000 s) |
 |
| Fig. 4 Time history of relative position (tf5 000 s) |
 |
| Fig. 5 Time history of relative velocity (tf5 000 s) |
Different from the example above,the final time is free and constrained less than 104 s in this example. The time history of specific charge is plotted in Fig. 6. It can be seen that the specific charge is mainly on the order of 10−4,which is less than the specific charge in the first example and is of course below the allowed maximum. Lagrange polynomial interpolation is also used to estimate the specific charges between the LG points,as denoted by the solid line in Fig. 6. The propellantless rendezvous is achieved at final time tf = 9 984.25 s and the cost function is J = 1.60 × 10−3. Compared with the first example,72.12% of the control energy is saved if the final time could be nearly doubled. The time histories of relative position and relative velocity during rendezvous process are shown in Figs. 7 and 8,respectively. Likewise, the trajectory of specific charge is substituted into the nonlinear dynamical model to evaluate the precision of the GPM,as shown by the solid lines in Figs. 7 and 8. The numerical results are also nearly coincided with the results obtained by the GPM,substantiating the validity and applicability of the GPM. The terminal relative position errors are 0.45 m,0.13 m,and 0.002 m in each axis,and the terminal relative velocity errors are,respectively,7.00×10−4 m/s, 9.52 × 10−4 m/s,and 3.97 × 10−5 m/s.
 |
| Fig. 6 Time history of specific charge (tf< 104 s) Fig. 7 Time history of relative position (tf< |
 |
| Fig. 7 Time history of relative position (tf< 104 s) |
 |
| Fig. 8 Time history of relative velocity (tf< 104 s) |
In this subsection,comparisons are made between the optimal solutions to the Lorentzpropelled rendezvous under different initial conditions. The initial orbital elements of the target spacecraft are selected as those shown in Table 1 and the initial phase angle of the tilted dipole is also set as 40◦. The final time is fixed at tf = 5 000 s and the number of the LG points is 50. The chaser is assumed to initially lead or trail the target in the in-track direction with no relative velocity. Therefore,the initial boundary constraints are given by
Denote |λ|mean and |λ|max as the mean and maximal absolute values of the required specific charge for rendezvous,respectively. Figure 9 illustrates the required values of |λ|mean,|λ|max, and J with different initial in-track relative distances. As can be seen,both mean and maximal specific charges increase with increasing initial in-track relative distances,and a similar trend is followed by the control-energy objective function. It can be concluded that the near-term maximal charging levels allow a rendezvous mission in low Earth orbit with the duration of nearly one orbital period and the initial in-track relative distance within several kilometers. Furthermore,numerical simulations indicate that the proposed method is more efficient for cases when the initial relative position is purely in-track due to the characteristics of the Lorentzpropelled relative motion,as those analyzed in our previous works[5, 24].
 |
| Fig. 9 Required mean and maximal absolute values of specific charge and objective functions for rendezvous with different initial in-track relative distances |
An energy-optimal strategy for spacecraft rendezvous in an inclined Earth orbit using a geomagnetic Lorentz force as the single propellantless propulsion is developed in this paper. Different from the previous Lorentz-force-propelled rendezvous strategies,this method is not limited to in-plane rendezvous in on equatorial orbit with restrictions on the initial relative states. The proposed nonlinear relative translational dynamics model of the Lorentz spacecraft, which incorporates both the inclination of the reference orbit and the magnetic dipole tilt angle,is more accordant with the actual property of the geomagnetic field. Thus,results derived from this model would be more precise than those obtained by the previous linearized models. Formulating the rendezvous trajectory optimization problem as an optimal control problem,it is then transformed into an NLP by the GPM and finally solved numerically by the SNOPT. Numerical simulation results validate the feasibility of the GPM in solving the Lorentz-force-propelled rendezvous with either fixed or free final time. Current research work is based on a two-body orbital model,future work would take the Earth oblateness effects and atmospheric drag into consideration to derive a more accurate rendezvous trajectory. Besides, a closed-loop controller remains to be designed to track the optimal reference trajectory.
Acknowledgements The authors express their gratitude to the reviewers and editors for their valuable and constructive comments that helped greatly enhance the quality of this paper. The first author wishes to acknowledge the encouragement and care given by his sincere friend,Shujian BU in Amazonas,USA.| [1] | Peck, M. A. Prospects and challenges for Lorentz-augmented orbits. AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, California, 2005-5995 (2005) |
| [2] | Pollock, G. E., Gangestad, J. W., and Longuski, J. M. Inclination change in low-Earth-orbit via the geomagnetic Lorentz force. Journal of Guidance, Control, and Dynamics, 33(5), 1387-1395 (2010) |
| [3] | Pollock, G. E., Gangestad, J. W., and Longuski, J. M. Analytical solutions for the relative motion of spacecraft subject to Lorentz-force perturbations. Acta Astronautica, 68(1-2), 204-217 (2011) |
| [4] | Yamakawa, H., Bando, M., Yano, K., and Tsujii, S. Spacecraft relative dynamics under the influence of geomagnetic Lorentz force. AIAA/AAS Astrodynamics Specialist Conference, Toronto, Ontario Canada, 2010-8128 (2010) |
| [5] | Huang, X., Yan, Y., Zhou, Y., and Yi, T. Improved analytical solutions for relative motion of Lorentz spacecraft with application to relative navigation in low Earth orbit. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 228(11), 2138-2154 (2014) |
| [6] | Huang, X., Yan, Y., and Zhou, Y. Dynamics and control of spacecraft hovering using the geomagnetic Lorentz force. Advances in Space Research, 53(3), 518-531 (2014) |
| [7] | Huang, X., Yan, Y., Zhou, Y., and Zhang, H. Sliding mode control for Lorentz-augmented spacecraft hovering around elliptic orbits. Acta Astronautica, 103(10-11), 257-268 (2014) |
| [8] | Peck, M. A., Streetman, B., Saaj, C. M., and Lappas, V. Spacecraft formation flying using Lorentz force. Journal of the British Interplanetary Society, 60(7), 263-267 (2007) |
| [9] | Peng, C., and Gao, Y. Lorentz-force-perturbed orbits with application to J2-invariant formation. Acta Astronautica, 77(8-9), 12-28 (2011) |
| [10] | Tsujii, S., Bando, M., and Yamakawa, H. Spacecraft formation flying dynamics and control using the geomagnetic Lorentz force. Journal of Guidance, Control, and Dynamics, 36(1), 136-148 (2013) |
| [11] | Wu, B., Wang, D., Poh, E. K., and Xu, G. Nonlinear optimization of low-thrust trajectory for satellite formation: Legendre pseudospectral method. Journal of Guidance, Control, and Dynamics, 32(4), 1371-1381 (2009) |
| [12] | Huntington, G. T. and Rao, A. V. Optimal reconfiguration of spacecraft formations using the Gauss pseudospectral method. Journal of Guidance, Control, and Dynamics, 31(3), 689-698 (2008) |
| [13] | Vaddi, S. S., Vadali., S. R., and Alfriend., K. T. Formation flying: accommodating nonlinearity and eccentricity perturbations. Journal of Guidance, Control, and Dynamics, 26(2), 214-223 (2003) |
| [14] | Benson, D. A., Huntington, G. T., Thorvaldsen, T. P., and Rao, A. V. Direct trajectory optimization and costate estimation via an orthogonal collocation method. Journal of Guidance, Control, and Dynamics, 29(6), 1435-1440 (2006) |
| [15] | Fahroo, F. and Ross, I. M. Costate estimation by a Legendre pseudospectral method. Journal of Guidance, Control, and Dynamics, 24(2), 270-277 (2001) |
| [16] | Fahroo, F. and Ross, I. M. Direct trajectory optimization by a Chebyshev pseudospectral method. Journal of Guidance, Control, and Dynamics, 25(1), 160-166 (2002) |
| [17] | Williams, P. Jacobi pseudospectral method for solving optimal control problems. Journal of Guidance, Control, and Dynamics, 27(2), 293-297 (2004) |
| [18] | Garg, D., Patterson, M. A., Francolin, C., Darby, C. L., Huntington, G. T., Hager, W. W., and Rao., A. V. Direct trajectory optimization and costate estiamtion of finite-horizon and infinitehorizon optimal control problems using a Radau pseudospectral method. Computational Optimization and Applications, 49(2), 335-358 (2011) |
| [19] | Darby, C. L., Hager, W. W., and Rao, A. V. Direct trajectory optimization using a variable loworder adaptive pseudospectral method. Journal of Spacecraft and Rockets, 48(3), 433-445 (2011) |
| [20] | Huntington, G. T., Benson, D., and Rao, A. V. A comparison of accuracy and computational efficiency of three pseudospectral method. AIAA Guidance, Navigation, and Control Conference and Exhibit, Hilton Head, South Carolina, 2007-6405 (2007) |
| [21] | Garg, D., Patterson, M., Hager, W. W., Rao, A. V., Benson, D. A., and Huntington, G. T. A unified framework for the numerical solution of optimal control problems using pseudospectral methods. Automatica, 46(11), 1843-1851 (2010) |
| [22] | Rao, A. V., Benson, D. A., Darby, C., Patterson, M. A., Francolin, C., Sanders, I., and Huntington, G. T. Algorithm 902: GPOPS, a Matlab software for solving multiple-phase optimal control problems using the Gauss pseudospectral method. ACM Transactions on Mathematical Software, 37(2), 1-39 (2010) |
| [23] | Gill, P. E., Murray, W., and Saunders, M. A. SNOPT: an SQP algorithm for large-scale constrained optimization. SIAM Journal on Optimization, 12(4), 979-1006 (2002) |
| [24] | Huang, X., Yan, Y., and Zhou, Y. Optimal control of Lorentz spacecraft rendezvous on circular equatorial orbit (in Chinese). Proceedings of the 32nd Chinese Control Conference, Xi'an, 26-28 (2013) |
 2015, Vol. 36
2015, Vol. 36






















