Shanghai University
Article Information
- M. AOUADI. 2015.
- On thermoelastic diffusion thin plate theory
- Appl. Math. Mech. -Engl. Ed., 36(5): 619-632
- http://dx.doi.org/10.1007/s10483-015-1930-7
Article History
- Received 2014-10-06;
- in final form 2015-01-28
Elastic plates are essential components that have highly important mechanical structures and,as such,have a large range of practical applications,in particular in industrial construction and microchip production. The thin plates,which are basic elements in various mechanical structures,can develop cracks due to wear of the material or by design. For this reason,the mechanical properties of such particular structures have been intensively studied in several papers[1, 2, 3, 4, 5]. For a long time,the effect of transverse shear forces has been ignored in the framework of the classical linear theory under Kirchhoff’s model[4]. Lately,however,the demand for more stringent accuracy created by the sophistication of industrial design and the advent of very powerful computers has led to a continuous increase in the use of the refined models. The refined models,where the field equations are much more complicated than in the old, classical one,take into account both the deflection of the middle section and the transverse shear forces. To justify their use,a rigorous mathematical analysis is necessary in order to settle the questions of well-posedness,analyticity and stability of the solution before numerical computations can be considered. It is worth recalling that such questions have been studied in several papers[6, 7, 8, 9, 10, 11, 12].
In this paper,these questions are further investigated,particularly when diffusion effects are considered in the thermoelastic thin plate theory. Thus,many consequent mechanical and mathematical problems need serious analysis.
Maybe we can think that the classical theory of thermoelastic thin plates is a good model to explain the thermal conduction in different structures. However,the research conducted in the development of high technologies after the second world war,confirmed that the field of diffusion in solids cannot be ignored. Thus,the obvious question is,what happens when the diffusion effect is considered with the thermal effect in the theory of thin elastic plate. Diffusion can be defined as the random walk of a set of particles from regions of high concentration to regions of lower concentration. Thermodiffusion in an elastic solid is due to coupling of the fields of strain,temperature,and mass diffusion. The processes of heat and mass diffusion play important roles in many engineering applications,such as satellites problems,returning space vehicles,and aircraft landing on water or land. There is now a great deal of interest in the process of diffusion in the manufacturing of integrated circuits,integrated resistors, semiconductor substrates,and MOS transistors. Oil companies are also interested to this phenomenon to improve the conditions of oil extractions.
The classic thermoelastic diffusion theory was introduced by Nowacki[13]. Later,Sherief et al.[14] established the generalized model with relaxation times. Recently,Aouadi et al.[15, 16, 17, 18, 19, 20] have derived the governing equations of some thermoelastic diffusion theories as well as some qualitative properties of the solutions. An overview of different models of this theory was presented in a survey article credited to Aouadi[21].
This paper aims to provide a consistent theory of homogeneous and isotropic thermoelastic diffusion thin plates. This work,which has not been obtained in any reference yet,represents a first step to understand the fundamental limits of intrinsic thermo-diffusion dissipations arising in elastic structures. However,the arguments of the classic theory can be adapted here to obtain the theory of thermoelastic diffusion thin plates under the Lagnese and Lions model[4] and according to Norris’ comments[5]. In Section 2,we develop the main points to obtain the equations of thermoelastic diffusion thin plate under three different models of heat and diffusion transmission. First the classical Fourier’s law is used to describe the thermo-diffusion conduction in the plate. Unfortunately,this law has a serious shortcoming. The corresponding parabolic part in both heat and diffusion equations predicts an unrealistic result: the thermal and diffusion disturbances at one point of the body are instantly felt everywhere in the body, that is they entail infinite propagation speeds. This observation leads one to look for other more general realistic models of transmission. Here,we write the equations of thermoelastic diffusion thin plate according to two generalized models of transmission. We consider the plate with second sound,that is,the distributions of the temperature and diffusion in the plate are described by Cattaneo’s law,instead of classical Fourier’s law of conduction. Then,we consider the case of plate with memory where we use the Gurtin-Pipkin’s law of conduction. Under both generalized models,thermal and diffusion disturbances propagate with finite speed,so that the corresponding equations are of hyperbolic types. In Section 3,using the C0-semigroup theory, we prove the well-posedness of the model derived in the frame of classic laws. 2 Basic equations and priliminaries
Following Nowacki[13],the basic governing equations of motion,heat and diffusion,in the absence of body forces,external loads,heat and diffusion sources,are given as follows.
(i) The equation of motion
(ii) The stress-strain-temperature-diffusion relation
(iii) The displacement-strain relation
(iv) The entropy-strain-temperature-diffusion relation
(v) The energy equation
(vi) The equation of conservation of mass
(vii) The chemical-strain-temperature-diffusion relation
where λ and μ are Lamé’s constants. β1 = (3λ + 2μ)αt and β2 = (3λ + 2μ)αc,where αt and αc are,respectively,the coefficients of linear thermal and diffusion expansion. θ = T − T0 is small temperature increment,where T is the absolute temperature of the medium,and T0 is the reference temperature. ρ is the mass density per unit volume,and cE is the specific heat at a constant strain. ui are the components of the displacement vector u,tij are the components of the symmetric stress tensor T,and eij are the components of the strain tensor. P is the chemical potential per unit mass,S is the entropy per unit mass,C is the concentration of the diffusive material in the elastic body,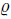 is a measure of diffusive effect,and w is a measure of
thermodiffusion effect.
is a measure of diffusive effect,and w is a measure of
thermodiffusion effect.
The expressions of heat and diffusion flux vectors q and p will be given later under three different models of transmission.
In the following sections,we need a different alternative form,where the chemical potential is used as a state variable instead of the concentration. From (7),we obtain
Substituting (8) into (1)-(6),we obtain the desired alternative form as follows: where are physical positive constants. It is easy to obtain from (10) that which implies that
We now consider a thermoelastic diffusion plate occupying the domain −∞ < x,y < ∞,
and  . We suppose that the thickness of the plate h is smaller in one order of magnitude
than its span or diameter so that it can be termed as a thin plate. Suppose also that the plate
is traction free on the surfaces: t13 = t23 = t33 = 0 on z = ±h/2.
. We suppose that the thickness of the plate h is smaller in one order of magnitude
than its span or diameter so that it can be termed as a thin plate. Suppose also that the plate
is traction free on the surfaces: t13 = t23 = t33 = 0 on z = ±h/2.
To describe what thin plates models has in common,we derive the motion equations. The first equation of (9) can be written as
The repeated Greeks indicate summation over 1 and 2. The development so far is independent of the models of heat and diffusion transmission. Integrating the first term of (12) with respect to z and using the fact that the shear and the normal stresses vanish on the surfaces yield[5] where w is the averaged through-thickness displacement, The in-plane equilibrium equation (the second term of (12)) then implies where the first moment of the stresses (or simply the moments) is given by According to the Kirchhoff hypothesis for thin plates,we consider the following assumptions:(i) The mid plane remains unstrained subsequent to bending.
(ii) Plane sections initially normal to the mid surface remain plane and normal to that after the bending. This means that we can take e13 = e23 = 0. The deflection of the plate is thus associated principally with bending strains. Consequently the normal strain e33,resulting from transverse loading,may be neglected.
(iii) The normal stress component t33 is much smaller than the other stress components and may also be neglected.
Thus,using the above assumptions (ii) and (iii),the symmetric stress tensor tαβ satisfies the following equations:
where δαβ is a metric tensor on the surface of the plate. From the second term of (17),we can obtain and from the third term of (17),we can obtainAccording to the assumption (ii),the strain-displacement relations become
Now,u3,3 = 0 implies that This means that the lateral deflection does not vary over the plate thickness. Integrating the expressions of e13 and e23 in (20) gives us From the assumption (i),one can deduce that u10 = u20 = 0,and consequently (22) becomes which confirms (18). Substituting (23) into (20),we get The divergence of ut appearing in (9) is given by

Furthermore,(15) becomes
where I = h3/12.(26) is the standard complete plate equation for elastic,thermoelastic,or thermoelastic diffusion plates.
Thus,substituting (19) and (23) into the constitutive relation (17),we obtain the extended traction equation as follows:
On the other hand,the expression of Mαβ given by (16) can be written in terms of w,Θ, and Φ as follows:
where are the first moments of temperature and chemical potential,respectively.Furthermore,(26) can be reduced to
where are provided by (28). Substituting (31) into (30),we get where(32) is the common equation of motion of a thermoelastic diffusion thin plate under any law of heat or diffusion transmission. When the diffusion effect is ignored (γ2 = 0),(32) reduces to the standard thermoelastic thin plate equation[2, 3, 4, 5].
In the following subsections,we complete (32) by the equations of heat and diffusion,under three different laws of heat and diffusion transmission,according to the corresponding Lagnese and Lions model[4] and the corrections and criticism made by Norris[5]. It is worth noting that the equation of motion (32) remains the same for the three following systems derived from the three different laws of transmission. 4 Thermo-diffusion thin plate equations
To complete (32) by the equations of heat and diffusion,we substitute (25) into (9),
where ν1 and ν2 are given by (33),andIt is easy to prove that the positive constants c*,k*,and r* verify (11). 4.1 Classic laws
Now,we write the heat and diffusion equations according to classic Fourier’s law for heat and Fick’s law for diffusion transmission,respectively,
where k is the coefficient of thermal conductivity,and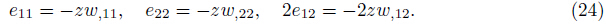 is the coefficient of diffusion conductivity.
is the coefficient of diffusion conductivity.
Substituting the divergence of (36) into (34),we conclude
Multiplying (37) by z and then integrating,we get
where Θ and Φ are defined by (29),and ξ1(x,y,t) and ξ2(x,y,t) are the first moments of θ,zz and P,zz,respectively,i.e., Applying the assumed zero flux conditions on the plate surfaces, yields In order to relate ξ1 to Θ,Lagnese and Lions[4] assumed that θ(x,y,z,t) is linear in z,i.e., Substituting (42) into the first equation of (41),we get Similarly,using the same arguments,we can obtainSubstituting (43) and (44) into (38),we get
Adding (32) to (45),we obtain the classical equations of thermoelastic diffusion thin plate in the frame of the Lagnese and Lions model,i.e.,
whereIt is worth noting that the positive coefficients 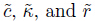 verify (11).
4.2 Cattaneo’s laws
verify (11).
4.2 Cattaneo’s laws
In this case,a modified law of heat conduction,the Cattaneo’s law[22],i.e.,
replaces the classic Fourier law (the first term of (36)). The positive parameter τ0 is the relaxation time describing the time lag in the response of the heat flux to a gradient in the temperature. Similarly,the second term of (36) is replaced by[14] where τ is the diffusion relaxation time,which will ensure that the equation satisfied by the concentration will also predict finite speeds of propagation of matter from one medium to the other.Substituting the divergence of (48) and (49) into (34),we conclude
Multiplying (50) by z and then integrating,we get where Θ and Φ are defined by (29),and ξ1 and ξ2 are given by (39)-(44). Substituting (43) and (44) into (51),we get Adding (32) to (52),we obtain the equations of thermoelastic diffusion thin plate under Cattaneo’s laws in the frame of Lagnese and Lions model where the coefficients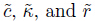 are given by (47). By using Cattaneo’s laws for heat and
diffusion transmissions,the last two terms of (53) become hyperbolic,and hence,automatically
eliminate the paradox of infinite speed. It is easy to see that (53) can be reduced to the classical
thin plate equation (46) by taking τ0 = τ = 0.
4.3 Gurtin-Pipkin’s law
are given by (47). By using Cattaneo’s laws for heat and
diffusion transmissions,the last two terms of (53) become hyperbolic,and hence,automatically
eliminate the paradox of infinite speed. It is easy to see that (53) can be reduced to the classical
thin plate equation (46) by taking τ0 = τ = 0.
4.3 Gurtin-Pipkin’s law
According to Gurtin-Pipkin’s theory[23],the linearized constitutive equations of q and p are given by[20, 24]
where k(s) and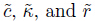 (s) are,respectively,heat and diffusion conductivity relaxation kernels.
Substituting the divergence of (54) into (34),we get
(s) are,respectively,heat and diffusion conductivity relaxation kernels.
Substituting the divergence of (54) into (34),we get
Multiplying (55) by z and then integrating,we get
Substituting (43) and (44) into (56),we get
Adding (32) to (57),we obtain the equations of thermoelastic diffusion thin plate with memory in the frame of Lagnese and Lions model
where the coefficients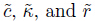 are given by (47). The convolution terms,appearing in (58),
introduced by Gurtin-Pipkin’s law entail the finite propagation speed for both thermal and
diffusion disturbances. (54) can be reduced to the classical Fourier’s law by taking k(s) =
are given by (47). The convolution terms,appearing in (58),
introduced by Gurtin-Pipkin’s law entail the finite propagation speed for both thermal and
diffusion disturbances. (54) can be reduced to the classical Fourier’s law by taking k(s) =
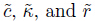 (s) = δ(s) (the Dirac distribution at zero). Besides,if we take
(s) = δ(s) (the Dirac distribution at zero). Besides,if we take

For the sake of brevity,we prove in the following section the well-posedness of the classical model only. 5 Well-posedness of classical model
In this section,we consider an open bounded domain  ,where the dimension d ≥ 2
may be arbitrary,but d = 2 corresponds to models derived in the previous section.
,where the dimension d ≥ 2
may be arbitrary,but d = 2 corresponds to models derived in the previous section.
We study the well-posedness of system (46) subject to initial conditions
We consider clamped boundary conditions for w and Dirichlet boundary condition for Θ and Φ,i.e., where v = (v2,v2,· · · ,vn) stands for the unit outer normal to ∂Ω,and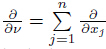 .
.
We now transform the initial-boundary-value problem given by (46),(59),and (60) to an abstract problem on a suitable Hilbert space.
Put wt = v in (46),and (46) is reduced to the system of equations
where I is the identity operator. SetThen,(61) can be written into the Sobolev equation,
where

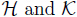 are the Hilbert spaces.
are the Hilbert spaces.
We define the inner products of 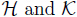 as follows:
as follows:

The following theorem is proved by using the same argument used in the proof of Theorem 11.11[25].
Theorem 5.1 The problem (63) is well-posed and is governed by a (C0) contraction semigroup on K.
Proof From Goldstein[25],it is sufficient to prove that 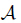 is a positive and self-adjoint
operator on
is a positive and self-adjoint
operator on 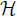 ,that 0 belongs to the resolvent set of
,that 0 belongs to the resolvent set of 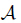 ,i.e.,0 ∈ ρ(
,i.e.,0 ∈ ρ(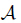 ),that
),that  ,
and that
,
and that  in a maximal dissipative operator on
in a maximal dissipative operator on 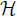 . Since it is easy and classic to prove that
0 ∈ ρ(
. Since it is easy and classic to prove that
0 ∈ ρ(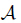 ),and that
),and that  ,we shall only prove that
,we shall only prove that 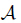 is a positive and self-adjoint
operator on
is a positive and self-adjoint
operator on 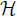 . For all
. For all  ,we have
,we have
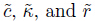 verify the condition (11),we deduce that
verify the condition (11),we deduce that  .
Let,then,ζ be a number chosen in such a way that
.
Let,then,ζ be a number chosen in such a way that 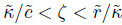 . Thus,the Cauchy-Schwartz
and Young’s inequalities lead to
Thus,(64) becomes
. Thus,the Cauchy-Schwartz
and Young’s inequalities lead to
Thus,(64) becomes

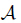 is a positive operator on
is a positive operator on 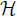 . Since
. Since

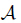 is self-adjoint on
is self-adjoint on 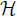 .
.
To prove that 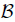 is a maximal dissipative operator on
is a maximal dissipative operator on 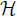 ,we have for all
,we have for all 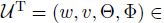
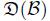

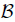 is a dissipative operator on
is a dissipative operator on 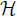 . To show R(I −B) =
. To show R(I −B) = 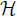 ,we shall prove the
existence of a vector of functions
,we shall prove the
existence of a vector of functions 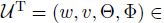
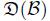 satisfying
which in terms of the components gives
satisfying
which in terms of the components gives


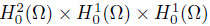 by
by

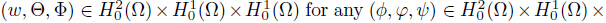 H01 (Ω). The bilinear form F is coercive,because
H01 (Ω). The bilinear form F is coercive,because


If we put φ = Φ = 0 in (69),






We summarize the obtained results as follows.
(i) We have derived the basic equations of thermoelastic diffusion thin plate under three different laws of heat and diffusion transmission according to the Lagnese and Lions model[4] and the corrections and criticism made by Norris[5].
(ii) We have proved the mathematical well-posedness for the proposed mechanical model of thermoelastic diffusion thin plates.
(iii) By comparison with other models proposed for thin plates,the model proposed in this paper is more reasonable in predicting the propagation of thermal,diffusion,and elastic waves in thin plates. We believe that the mechanical and mathematical results presented can reveal the usefulness of this model in many engineering applications,which is exactly what this paper aims at.
| [1] | Chadwick, P. On the propagation of thermoelastic disturbances in thin plates and rods. Journal of the Mechanics and Physics of Solids, 10, 99-109 (1962) |
| [2] | Inan, E. Coupled theory of thermoelastic plates. Acta Mechanica, 14, 1-29 (1972) |
| [3] | Timoshenko, S. and Woinowsky-Krieger, S. Theory of Plates and Shells, McGraw-Hill, New York (1987) |
| [4] | Lagnese, J. E. and Lions, J. L. Modelling Analysis and Control of Thin Plates, Masson, Paris (1988) |
| [5] | Norris, A. N. Dynamics of thermoelastic thin plates: a comparison of four theories. Journal of Thermal Stresses, 29, 169-195 (2006) |
| [6] | Kim, J. U. On th energy decay of a linear thermoelastic bar and plate. SIAM Journal on Mathematical Analysis, 23, 889-899 (1992) |
| [7] | Liu, Z. and Renardy, M. A note on the equation of a thermoelastic plate. Applied Mathematics Letters, 8, 1-6 (1995) |
| [8] | Rivera, J. E. M. and Fatori, L. H. Regularizing properties and propagations of singularities for thermoelastic plates. Mathematical Methods in the Applied Sciences, 21, 797-821 (1998) |
| [9] | Avalos, G. and Lasiecka, I. The null controllability of thermoelastic plates and singularity of the associated minimal energy function. Journal of Mathematical Analysis and Applications, 294, 34-61 (2004) |
| [10] | Chai, S. and Guo, B. Z. Analyticity of a thermoelastic plate with variable coefficients. Journal of Mathematical Analysis and Applications, 354, 330-338 (2009) |
| [11] | Liu, Z. and Quitanilla, R. Analyticity of solutions in type III thermoelastic plates. IMA Journal of Applied Mathematics, 75, 637-646 (2010) |
| [12] | Zelati, M. C., Dell'Oro, F., and Pata, V. Energy decay of type III linear thermoelastic plates with memory. Journal of Mathematical Analysis and Applications, 401, 357-366 (2013) |
| [13] | Nowacki, W. Dynamical problems of thermoelastic diffusion in solids I. Bulletin of the Polish Academy of Sciences Technical Sciences, 22, 55-64 (1974) |
| [14] | Sherief, H., Hamza, F., and Saleh, H. The theory of generalized thermoelastic diffusion. International Journal of Engineering Science, 42, 591-608 (2004) |
| [15] | Aouadi, M. The coupled theory of micropolar thermoelastic diffusion. Acta Mechanica, 208, 181-203 (2009) |
| [16] | Aouadi, M. Theory of generalized micropolar thermoelastic diffusion under Lord-Shulman model. Journal of Thermal Stresses, 32, 923-942 (2009) |
| [17] | Aouadi, M. A theory of thermoelastic diffusion materials with voids. Zeitschrift für Angewandte Mathematik und Physik, 61, 357-379 (2009) |
| [18] | Aouadi, M. Qualitative results in the theory of thermoelastic diffusion mixtures. Journal of Thermal Stresses, 33, 595-615 (2010) |
| [19] | Aouadi, M., Lazzari, B., and Nibbi, R. A theory of thermoelasticity with diffusion under Green-Naghdi models. Zeitschrift für Angewandte Mathematik und Mechanik, 94, 837-852 (2014) |
| [20] | Aouadi, M., Lazzari, B., and Nibbi, R. Energy decay in thermoelastic diffusion theory with second sound and dissipative boundary. Meccanica, 48, 2159-2171 (2013) |
| [21] | Aouadi, M. Classic and generalized thermoelastic diffusion theories. Encyclopedia of Thermal Stresses, Springer Science and Business Media, Dordrecht (2013) |
| [22] | Cattaneo, C. Sulla conduzione del calore. Atti del Seminario Matematico e Fisico dell' Università di Modena, 3, 83-101 (1948) |
| [23] | Gurtin, M. E. and Pipkin, A. C. A general theory of heat conduction with finite wave speeds. Archive for Rational Mechanics and Analysis, 31, 113-126 (1968) |
| [24] | Ezzat, M. and Awad, E. Theory of heat and mass transfer in viscoelastic solids with microstructures. Journal of Thermal Stresses, 34, 795-816 (2011) |
| [25] | Goldstein, J. A. Semigroups of Linear Operators and Applications, Oxford University Press, New York (1985) |
 2015, Vol. 36
2015, Vol. 36





































































