Shanghai University
Article Information
- S. A. SHEHZAD, T. HAYAT, A. ALSAEDI, B. AHMAD. 2015.
- Effects of thermophoresis and thermal radiation in mixed convection three-dimensional flow of Jeffrey fluid
- Appl. Math. Mech. -Engl. Ed., 36(5): 655-668
- http://dx.doi.org/10.1007/s10483-015-1935-7
Article History
- Received 2014-02-28;
- in final form 2014-09-26
2. Department of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan;
3. Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia
The flow of non-Newtonian fluids has acquired a special status in recent years. There is an opinion of the investigators that most commonly used fluids in the industry and technology show non-Newtonian behaviors. Many of materials inbiological sciences, chemical and petroleum industries, geophysics, etc. also fall in the category of non-Newtonian fluids. Non-Newtonian fluids can be further classified into different classes, namely, differential, rate, and integral types. In the realm of non-Newtonian fluids, the fluids which display the behavior of elastic and memory effects are known as the rate type fluids [1,2,3,4,5] . A simplest subclass known as Jeffrey fluid exhibits both the elastic and memory effects. Srinivas and Muthuraj [6] investigated the peristaltic flow of Jeffrey fluid in a wave frame of reference moving with the wave speed. Series solutions for two-dimensional boundary layer flow of Jeffrey fluid near a stagnation point with heat transfer were constructed by Hayat et al. [7] . Partial slip effects on peristaltic transport of Jeffrey fluid in a tube were discussed by Nadeem et al. [8] . They presented both numerical and analytical solutions in their study. Hayat et al. [9] discussed the laminar flow of Jeffrey fluid with variable thermal conductivity. Exact analytical solutions for an incompressible flow of Jeffrey fluid with heat transfer were provided by Turkyilmazoglu and Pop [10] .
In view of engineering applications, the effects of heat and mass transfer on the flow past a stretching surface have attracted the attention of theoretical researchers. Few examples of such applications may include damage of cropsdue to freezing, cooling towers, food processing, cooling of metallic sheets in a cooling bath, human transpiration, refrigeration and air conditioning, desalination, etc. In addition, it is commonly known that the radiation effects have a superficial role at high operating temperatures in many engineering applications under the circumstances where heat transfer coefficients are small and in non-isothermal situations. If the whole system involving the polymer extrusion is kept in a thermally controlled environment in a polymer processing industry, the thermal radiation effects are quite useful for controlling and adjusting the heat transfer rate [11] . There are various investigations on the radiative flow with heat/mass transfer. A few recent and interesting studies can be seen in Refs. [12,13,14,15,16,17,18].
The term depicts the fact that small micron sized particles suspended in a non-isothermal gas can acquire a velocity in the direction of decreasing temperature, which is known as the thermophoresis [19] . The gas molecules coming from the cold side has lower velocity when compared with those coming from the hotter side [20] . The molecules moving with higher velocity make a collision with the particles more forcefully. This produces a difference in the momentum. Due to this difference, the particle produces a velocity in the direction of lower temperature [21] . The velocity gained by the particles is called the thermophoretic velocity and the force is known as the thermophoretic force [22] . Such effects are significant in the blackening of glass globe of kerosene lanterns, chimneys, and industrial furnace walls by carbon particles. The concept of thermophoresis is utilized to manufacture graded index silicon dioxide and germanium dioxide optical fiber preforms used in the field of communications [23] .
It has been noted from the existing literature that two-dimensional boundary layer flows have been examined extensively without thermophoresis. Only few attempts have been made for the two-dimensional flows in the presence of thermophoresis [19,20,21,22,23] . On the other hand, the mixed convection three-dimensional flow of non-Newtonian fluid with both heat and mass transfer is not analyzed yet. Hence, the objective here is to provide more general flow analysis in this regime. Therefore, attempt is made here to discuss the mixed convection three-dimensional flow of non-Newtonian fluid over a stretching surface with heat and mass transfer. Further, the thermophoresis and thermal radiation effects are taken into account. The convergent series solutions via the homotopy analysis method (HAM) [24,25,26,27,28,29,30] are constructed for the velocity, temperature, and concentration. Variations of interesting physical parameters are examined via graphs. Numerical values of local Nusselt and Sherwood numbers are computed and analyzed. 2 Statement of problem
We consider a three-dimensional laminar flow of an incompressible Jeffrey fluid over a stretching sheet at z =0. The flow occupies the domain z>0. The flow is generated due to the stretching sheet. Heat and mass transfer effects are considered. The wall temperature Twis greater than the ambient fluid temperature T∞. We consider the radiation effects by the Rosseland approximation. The governing boundary layer equations for velocity, temperature, and concentration are given as follows [19,31,32] :
where u, v, andw are the velocity components in the x-, y-, and z-directions, respectively,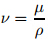 is the kinematic viscosity, ρ is the density of fluid, μis the dynamic viscosity of fluid, λ1 is the
ratio of relaxation and retardation times, λ2 is the retardation time, g is the acceleration due to
gravity, βTis the thermal expansion coefficient, βC is the concentration expansion coefficient,
T is the fluid temperature, k is the thermal conductivity of the fluid, qr is the radiative heat
flux, D is the molecular diffusivity of the concentration species, andVTis the thermophoretic
velocity.
is the kinematic viscosity, ρ is the density of fluid, μis the dynamic viscosity of fluid, λ1 is the
ratio of relaxation and retardation times, λ2 is the retardation time, g is the acceleration due to
gravity, βTis the thermal expansion coefficient, βC is the concentration expansion coefficient,
T is the fluid temperature, k is the thermal conductivity of the fluid, qr is the radiative heat
flux, D is the molecular diffusivity of the concentration species, andVTis the thermophoretic
velocity.
The subjected boundary conditions are as follows [32] :
where a and b have the dimension t-1 , and t is time.
The radiative heat flux qr via the Rosseland approximation can be written as  We assume a small temperature difference within the fluid flow in such a manner thatT4
can
be defined as a linear function of temperature. Expansion of T4
using Taylor’s series about a
free stream temperature T∞ is given as follows
[20]
:
We assume a small temperature difference within the fluid flow in such a manner thatT4
can
be defined as a linear function of temperature. Expansion of T4
using Taylor’s series about a
free stream temperature T∞ is given as follows
[20]
:

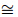 4T∞3T−3T∞4. Now, (4) has the following form:
The thermophoretic velocity VT can be defined as
where Tr is the reference temperature, and k*
is the thermophoretic coefficient.
4T∞3T−3T∞4. Now, (4) has the following form:
The thermophoretic velocity VT can be defined as
where Tr is the reference temperature, and k*
is the thermophoretic coefficient.
By taking the transformations
(1) is automatically satisfied. (2)-(7) yield where β1 =λ2ais the Deborah number,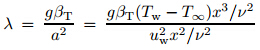 is the thermal
buoyancy parameter,
is the thermal
buoyancy parameter, 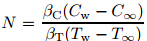 is the concentration buoyancy parameter,
is the concentration buoyancy parameter, 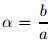 is
the ratio of stretching rates,
is
the ratio of stretching rates, 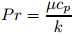 is the Prandtl number,
is the Prandtl number, 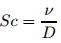 is the Schmidt number,
and
is the Schmidt number,
and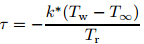 is the thermophoretic parameter.
is the thermophoretic parameter.
The quantities of physical interest are the local Nusselt and local Sherwood numbers. These in dimensionless forms are given as follows:
in which Rex=uw(x)x/ν is the local Reynolds number. 3 Homotopy analysis solutionsIn order to proceed for the homotopyanalysis solutions, we selectthe following initial guesses and auxiliary linear operators:
where Ci (i=1, 2, ···, 10) depict the arbitrary constants.The zeroth-order problems can be defined as follows:
in which p indicates an embedding parameter, and the non-zero auxiliary parameters are denoted by f,
f,  g,
g,  θ, and
θ, and  φ. Nf, Ng, N0, and Nφ show the nonlinear operators. For p=0
andp=1, we have
and when p increases from 0 to 1, f(η, p), g(η, p), θ(η, p), and φ(η, p)varyfrom f0(η), g0(η),
θ0(η), and φ0(η)to f(η), g(η), θ(η), and φ(η). Taylor’s series expansion gives us
φ. Nf, Ng, N0, and Nφ show the nonlinear operators. For p=0
andp=1, we have
and when p increases from 0 to 1, f(η, p), g(η, p), θ(η, p), and φ(η, p)varyfrom f0(η), g0(η),
θ0(η), and φ0(η)to f(η), g(η), θ(η), and φ(η). Taylor’s series expansion gives us
The convergence analysis in the series strongly depends on  f,
f,  g,
g,  θ, and
θ, and  φ. We select
φ. We select
 f,
f,  g,
g,  θ, and
θ, and  φ in such a manner that the series in (32)-(35) converge at p= 1. Hence,
(32)-(35) become
φ in such a manner that the series in (32)-(35) converge at p= 1. Hence,
(32)-(35) become
We have a great freedom in the HAM to select the auxiliary parameters f,
f,  g,
g,  θ, and
θ, and φ,
which are responsible for adjusting and controlling the convergence of homotopic solutions. To
obtain the suitable convergence region, we plot the
φ,
which are responsible for adjusting and controlling the convergence of homotopic solutions. To
obtain the suitable convergence region, we plot the -curves at 18th-order of approximations.
It is found from Figs. 1 and 2 that the ranges of admissible values of
-curves at 18th-order of approximations.
It is found from Figs. 1 and 2 that the ranges of admissible values of  f,
f,  g,
g,  θ, and
θ, and φ are
−0. 62≤
φ are
−0. 62≤ f−0. 10, −0. 60≤
f−0. 10, −0. 60≤ g≤ −0. 10, −0. 65≤
g≤ −0. 10, −0. 65≤ θ ≤−0. 10, and−0. 70≤
θ ≤−0. 10, and−0. 70≤ φ≤−0. 20.
Further, our series solutions converge in the whole region of η when
φ≤−0. 20.
Further, our series solutions converge in the whole region of η when f =
f = g =−0. 4and
g =−0. 4and
 θ=
θ= φ=−0. 5.
φ=−0. 5.
Table 1 includes numerical values of −f´´ (0), −g´´ (0), −θ´ (0), and −φ´ (0)atdifferentorders of approximations with

 |
Fig. 1  -curves for functionsf(η)andg(η)at
18th-order of deformations whenλ1=
0. 5, β=λ=Rd=0.4, N=0.3, Pr=1. 5, Sc=1. 0, α=0.5, andτ=0.2 -curves for functionsf(η)andg(η)at
18th-order of deformations whenλ1=
0. 5, β=λ=Rd=0.4, N=0.3, Pr=1. 5, Sc=1. 0, α=0.5, andτ=0.2 |
 |
Fig. 2  -curves for functions θ(η)andφ(η)at
18th-order of deformations whenλ1=
0. 5, β=λ=Rd=0.4, N=0.3, Pr=1. 5, Sc=1. 0, α=0.5, andτ=0.2 -curves for functions θ(η)andφ(η)at
18th-order of deformations whenλ1=
0. 5, β=λ=Rd=0.4, N=0.3, Pr=1. 5, Sc=1. 0, α=0.5, andτ=0.2 |
 f =
f = g =−0. 4, and
g =−0. 4, and
 θ=
θ= φ=−0. 5
φ=−0. 5  |
Table 2 is computed to analyze the numerical values of local Nusselt number −NuRex−1/2 and local Sherwood number −ShRex−1/2 for different values of λ1, λ, N, β1, Pr, Sc, and Rd whenτ=0.2 and α=0.5. The values of local Nusselt number are small in comparison to the local Sherwood number corresponding toλ1. The values of local Nusselt and Sherwood numbers are increased with λ and N.
 |
Figures 3 and 4 are plotted to show the variations of the velocities f' (η)and g' (η)fordifferent values of thermal buoyancy parameter λ. The velocities and their momentum boundary layer thicknesses are increased by increasing the thermal buoyancy parameter. Larger values of thermal buoyancy parameter correspond to stronger buoyancy forces. There is a favorable pressure gradient due to the buoyancy force that leads to an accelerated fluid flow. It is further noted that an increase in the velocityf' (η) is more dominant in comparison to the velocity g' (η).
 |
| Fig. 3 Effect of λ on velocity f' (η)vs η whenλ1 =0.5, β=Rd=0.4, N=0.3, Pr=1. 4, Sc=1. 2, α=0.5, and τ=0.1 |
 |
| Fig. 4 Effect of λ on velocity g' (η)vsη whenλ1 =0.5, β=Rd=0.4, N=0.3, Pr=1. 4, Sc=1. 2, α=0.5, and τ=0.1 |
Effects of the concentration buoyancy parameter N on the velocities are analyzed in Figs. 5 and 6. Here, one can see that the fluid velocities are enhancing due to an increase in the concentration buoyancy parameter. An increase in the concentration buoyancy parameter corresponds to an increase in the temperature difference. This provides an enhancement in the fluid velocities due to increase in the convection current. It is observed that the boundary layer thicknesses are thinner for lower values of concentration buoyancy parameter.
 |
| Fig. 5 Effect ofNon velocity f' (η)vsηwhen λ1=0.5, β=Rd=0.4, λ=0.3, Pr=1. 4, Sc=1. 2, α=0.5, andτ=0.1 |
 |
| Fig. 6 Effect ofNon velocity g' (η)vsηwhen λ1=0.5, β=Rd=0.4, λ=0.3, Pr=1. 4, Sc=1. 2, α=0.5, andτ=0.1 |
Figures 7 and 8 are portrayed to see the behaviors of the Prandtl numberPron the fluid velocities. The fluid velocities and momentum boundary layer thicknesses are reduced for larger values of the Prandtl number.
 |
| Fig. 7 Effect ofPron velocity f' (η)vsη whenλ1 =0.5, β=Rd=0.4, λ = N =0.3, Sc =1. 2, α =0.5, and τ=0.1 |
 |
| Fig. 8 Effect ofPron velocity g' (η)vsη whenλ1 =0.5, β=Rd=0.4, λ = N =0.3, Sc =1. 2, α =0.5, and τ=0.1 |
Figures 9 and 10 show the velocity distributions for various values of radiation parameter Rd. It is noticed from these figures that the velocities are smaller for lower values of radiation parameter.
 |
| Fig. 9 Effect ofRd on velocity f' (η)vsη whenλ1 =0.5, β=0.4, λ =N= 0. 3, Pr=1. 4, Sc=1. 2, α=0.5, and τ=0.1 |
 |
| Fig. 10 Effect ofRd on velocity g' (η)vsη whenλ1 =0.5, β=0.4, λ =N= 0. 3, Pr=1. 4, Sc=1. 2, α=0.5, and τ=0.1 |
To examine the effects of different interesting parameters on the temperature θ(η), we sketch Figs. 11-15. Figures 11 and12 illustrate the effects of thermalbuoyancy parameter and concentration buoyancy parameter on the temperature. It is seen that the temperature and thermal boundary layer thickness are reduced for the larger values of thermal and concentration buoyancy parameters. An increase in thermal and concentration buoyancy parameters provides an increase in the temperature difference (Tw−T∞) that leads to a lower temperature and thinner thermal boundary layer thickness.
 |
| Fig. 11 Effect of λon temperature θ(η)vsη whenλ1 =0.5, β=Rd=0.4, N=0.3, Pr=1. 4, Sc=1. 2, α=0.5and τ=0.1 |
 |
| Fig. 12 Effect ofN on temperature θ(η)vs ηwhenλ1 =0.5, β=Rd=0.4, λ= 0. 3, Pr=1. 4, Sc=1. 2, α=0.5and τ=0.1 |
 |
| Fig. 13 Effect ofPron temperature θ(η)vs ηwhenλ1=0.5, β=Rd=0.4, N= λ=0.3, Sc=1. 2, α=0.5, andτ=0.1 |
 |
| Fig. 14 Effect ofRd on temperature θ(η)vs ηwhenλ1 =0.5, β=0.4, N =λ= 0. 3, Pr=1. 4, Sc=1. 2, α=0.5, and τ=0.1 |
 |
| Fig. 15 Effect ofτ on concentrationφ(η)vsηwhenλ1=0.5, β=Rd=0.4, N=λ=0.3, Pr=1. 4, Sc=1. 2, andα=0.5 |
Figure 13 depicts that the temperature and thermal boundary layer thickness are higher for smaller values of the Prandtl number. The Prandtl number is the ratio of momentum to thermal diffusivity. Smaller Prandtl fluids have higher thermal conductivities so that heat can diffuse from the wall faster in comparison to higher Prandtl fluids. Thus, the Prandtl number can be used for the rate of cooling in the fluids. An increase in the radiation parameter enhances the temperature and thermal boundary layer thickness (see Fig. 14).
Physically, higher values of radiation parameter provide more heat to the fluid that caused an enhancement in the temperature. The concentration distribution for different values of thermophoretic parameter is seen from Fig. 15. We analyze that the concentration is increased for the increasing values of thermophoretic parameter.
The effect of the Schmidt number on the concentration is analyzed in Fig. 16. An increase in the Schmidt number yields a lower concentration and thinner concentration boundary layer thickness.
 |
| Fig. 16 Effect ofScon concentrationφ(η)vsηwhenλ1 =0.5, β=Rd=0.4, N=λ=0.3, Pr=1. 4, τ=0.1, andα=0.5 |
We have investigated the mixed convection three-dimensional flow of Jeffrey fluid over a surface with heat and mass transfer. Effects of thermal radiation and thermophoresis are also taken into account. The main points of this investigation are as follows.
(i) For convergent series solutions, 25th-order deformations are sufficient.
(ii) Velocitiesf' (η)andg' (η) are increased for larger valuesof thermal and concentration buoyancy parameter.
(iii) An increase in radiation parameter yields an enhancement in the velocities and temperature.
(iv) Fluid velocities and temperature corresponding to smaller values of the Prandtl number are larger.
(v) The thermophoretic parameter has quite opposite effects on the temperature and concentration.
(vi) The concentration boundary layer thickness is a decreasing function of the Schmidt number.
Acknowledgements The useful suggestions of reviewer are gratefully acknowledged. The authors also thank the DSR technical and financial support.| [1] | Fetecau, C., Zierep, J., Bohning, R., and Fetecau, C. On the energetic balance for the flow of an Oldroyd-B fluid due to a flat plate subject to a time-dependent shear stress. Computers Mathematics with Applications, 60, 74-82 (2010) |
| [2] | Wang, S. and Tan, W. C. Stability analysis of soret-driven double-diffusive convection of Maxwell fluid in a porous medium. International Journal of Heat and Fluid Flow, 32, 88-94 (2011) |
| [3] | Qi, H. and Jin, H. Unsteady helical flows of a generalized Oldroyd-B fluid with fractional derivative. Nonlinear Analysis: Real World Applications, 10, 2700-2708 (2009) |
| [4] | Hayat, T., Shehzad, S. A., Qasim, M., and Obaidat, S. Steady flow of Maxwell fluid with convective boundary conditions. Zeitschrift für Naturforschung A, 66a, 417-422 (2011) |
| [5] | Hayat, T., Shehzad, S. A., Mustafa, M., and Hendi, A. A. MHD flow of an Oldroyd-B fluid through a porous channel. International Journal of Chemical Reactor Engineering, 10, 1542-1580 (2012) |
| [6] | Srinivas, S. and Muthuraj, R. Peristaltic transport of a Jeffery fluid under the effect of slip in an inclined asymmetric channel. International Journal of Applied Mechanics, 2, 437-455 (2010) |
| [7] | Hayat, T., Shehzad, S. A., Qasim, M., and Obaidat, S. Thermal radiation effects on the mixed convection stagnation-point flow in a Jeffery fluid. Zeitschrift für Naturforschung A, 66a, 606-614 (2011) |
| [8] | Nadeem, S., Akbar, N. S., and Naz, T. The numerical and analytical solution of peristaltic flow of a Jeffery fluid in an inclined tube with partial slip. Journal of Mechanics in Medicine and Biology, 11, 773-802 (2011) |
| [9] | Hayat, T., Shehzad, S. A., Qasim, M., and Alsaedi, A. Radiative flow with variable thermal conductivity in porous medium. Zeitschrift für Naturforschung A, 67a, 153-159 (2012) |
| [10] | Turkyilmazoglu, M. and Pop, I. Exact analytical solutions for the flow and heat transfer near the stagnation point on a stretching/shrinking sheet in a Jeffrey fluid. International Journal of Heat and Mass Transfer, 57, 82-88 (2013) |
| [11] | Turkyilmazoglu, M. Analytic heat and mass transfer of the mixed hydrodynamic/thermal slip MHD viscous flow over a stretching sheet. International Journal of Mechanical Sciences, 53, 886-896 (2011) |
| [12] | Pal, D. Heat and mass transfer in stagnation-point flow towards a stretching surface in the presence of buoyancy force and thermal radiation. Meccanica, 44, 145-158 (2009) |
| [13] | Bhattacharyya, K. Effects of radiation and heat source/sink on unsteady MHD boundary layer flow and heat transfer over a shrinking sheet with suction/injection. Frontiers in Chemical Sciences and Engineering, 5, 376-384 (2011) |
| [14] | Ashraf, M., Asghar, S., and Hossain, M. A. Computational study of combined effects of conductionradiation and hydromagnetics on natural convection flow past magnetized permeable plate. Applied Mathematics and Mechanics (English Edition), 33,731-748(2012)DOI 10.1007/s10483-012-1583-7 |
| [15] | Mukhopadhyay, S. and Gorla, R. S. R. Effects of partial slip on boundary layer flow past a permeable exponential stretching sheet in presence of thermal radiation. Heat and Mass Transfer, 48, 1773-1781 (2012) |
| [16] | Makinde, O. D. Heat and mass transfer by MHD mixed convection stagnation point flow toward a vertical plate embedded in a highly porous medium with radiation and internal heat generation. Meccanica, 47, 1173-1184 (2012) |
| [17] | Moradi, A., Ahmadikia, H., Hayat, T., and Alsaedi, A. On mixed convection-radiation interaction about an inclined plate through a porous medium. International Journal of Thermal Science, 64, 129-136 (2013) |
| [18] | Turkyilmazoglu, M. and Pop, I. Heat and mass transfer of unsteady natural convection flow of some nanofluids past a vertical infinite flat plate with radiation effect. International Journal of Heat and Mass Transfer, 59, 167-171 (2013) |
| [19] | Muhaimin, I., Kandasamy, R., and Hashim, I. Thermophoresis and chemical reaction effects on non-Darcy MHD mixed convective heat and mass transfer past a porous wedge in the presence of variable stream condition. Chemical Engineering Research and Design, 87, 1527-1535 (2009) |
| [20] | Noor, N. F. M., Abbasbandy, S., and Hashim, I. Heat and mass transfer of thermophoretic MHD flow over an inclined radiate isothermal permeable surface in the presence of heat source/sink. International Journal of Heat and Mass Transfer, 55, 2122-2128 (2012) |
| [21] | Chamkha, A. J., Al-Muhaf, A. F., and Pop, I. Effect of heat generation or absorption on thermophoretic free convection boundary layer from a vertical flat plate embedded in a porous medium. International Communications in Heat and Mass Transfer, 33, 1096-1102 (2006) |
| [22] | Hayat, T. and Alsaedi, A. On thermal radiation and Joule heating effects in MHD flow of an Oldroyd-B fluid with thermophoresis. Arabian Journal of Science and Engineering, 36, 1113-1124 (2011) |
| [23] | Alam, M. S., Rahman, M. M., and Sattar, M. A. Similarity solutions for hydromagnetic free convective heat and mass transfer flow along a semi-infinite permeable inclined flat plate with heat generation and thermophoresis. Nonlinear Analysis: Modelling and Control, 12, 433-445 (2007) |
| [24] | Liao, S. J. Notes on the homotopy analysis method: some definitions and theorems. Communications in Nonlinear Science and Numerical Simulation, 14, 983-997 (2009) |
| [25] | Liao, S. J. A general approach to get series solution of non-similarity boundary-layer flows. Communications in Nonlinear Science and Numerical Simulation, 14, 2144-2159 (2009) |
| [26] | Turkyilmazoglu, M. A note on the homotopy analysis method. Applied Mathematics Letters, 23, 1226-1230 (2010) |
| [27] | Zhang, X., Tang, B., and He, Y. Homotopy analysis method for higher-order fractional integrodifferential equations. Computers Mathematics with Applications, 62, 3194-3203 (2011) |
| [28] | Hayat, T., Shehzad, S. A., Alsaedi, A., and Alhothuali, M. S. Mixed convection stagnation point flow of Casson fluid with convective boundary conditions. Chinese Physics Letters, 29, 114704 (2012) |
| [29] | Rashidi, M. M., Rajvanshi, S. C., and Keimanesh, M. Study of Pulsatile flow in a porous annulus with the homotopy analysis method. International Journal of Numerical Methods for Heat and Fluid Flow, 22, 971-989 (2012) |
| [30] | Hayat, T., Shehzad, S. A., and Alsaedi, A. Soret and Dufour effects in magnetohydrodynamic (MHD) flow of Casson fluid. Applied Mathematics and Mechanics (English Edition), 33, 1301-1312 (2012) DOI 10.1007/s10483-012-1623-6 |
 2015, Vol. 36
2015, Vol. 36


















