Shanghai University
Article Information
- Shulun LIU, Fan WANG, Renhuai LIU. 2015.
- Fluid flow and fluid shear stress in canaliculi induced by external mechanical loading and blood pressure oscillation
- Appl. Math. Mech. -Engl. Ed., 36(5): 681-692
- http://dx.doi.org/10.1007/s10483-015-1932-7
Article History
- Received 2014-09-22;
- in final form 2015-03-13
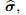 total stress vector for entire medium;
total stress vector for entire medium;
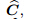 drained elasticity tensor;
drained elasticity tensor;
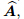 Biot effective stress coefficient vector;
Biot effective stress coefficient vector;
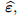 apparent strain tensor of solid matrix;
Λ, reciprocal of Biot modulus;
p, interstitial fluid pressure;
ζ, fluid content variation;
k, intrinsic Darcy’s law permeability;
μ, fluid viscosity;
ω, axial loading frequency;
Ω, blood pressure frequency;
In, first kind modified Bessel function of ordern;
Kn, second kind modified Bessel function of
ordern;
λ, dimensionless spatial variable;
α, specificvalueofλ;
φ, porosity;
ε0, strain amplitude;
Kff, permeability;
Kf
, compressibility;
pBO
, blood pressure amplitude;
a, ratio of osteon inner radius and outer radius;
l, length of canaliculi;
u, fluid velocity vector;
ρ, interstitial fluid density.
1 Introduction
apparent strain tensor of solid matrix;
Λ, reciprocal of Biot modulus;
p, interstitial fluid pressure;
ζ, fluid content variation;
k, intrinsic Darcy’s law permeability;
μ, fluid viscosity;
ω, axial loading frequency;
Ω, blood pressure frequency;
In, first kind modified Bessel function of ordern;
Kn, second kind modified Bessel function of
ordern;
λ, dimensionless spatial variable;
α, specificvalueofλ;
φ, porosity;
ε0, strain amplitude;
Kff, permeability;
Kf
, compressibility;
pBO
, blood pressure amplitude;
a, ratio of osteon inner radius and outer radius;
l, length of canaliculi;
u, fluid velocity vector;
ρ, interstitial fluid density.
1 Introduction Cortical bone is regarded as the material tissue or structure system, and its basic unit is osteon. Osteon is a kind of porous biological material and can be seen as consisting of a tight layer of elastic bone plates and intertwined and micro-tubes filled with fluid system. The micro-tubes are called canaliculi. The Wolff Law [1] points out that bone tissue, as a living entity, can sense, react, and adapt its structure to its external environment. Bone resorption and generation are the result of a series of events transforming a physical information into a biological response. This process is called bone mechanotransduction. In order to clarify the mechanism, the osteon must be explored, because the process may be associated with a series of effects generated by the fluid flow in bone tissue, such as pressure distribution in bone, chemical transportation, and fluid shear stress. Thus, an investigation of the fluid flow and fluid shear stress in the canaliculi is very necessary.
Poroelasticity theory first proposed by Biot
[2]
is widely used in the porous material with
the solid-liquid coupling. Therefore, the poroelasticity theory can be used to describe the osteon in theory. Some researchers
[3, 4]
have established the theoretical model of osteon according
to this theory. They regarded bone plate layer as an elastic solid and its internal pore and
microtubule as pore containing liquid. R mond and Naili[5]
modeled an osteon, a basic unit
of cortical bone, as a hollow cylinder and solved the poroelastic problem of the osteon under
cyclic loading. Wang et al.
[6, 7, 8]
described the buckling and creep buckling of biologic bone in
the form of a cylindrical shell. Wu et al.
[9, 10, 11]
proposed a new model of transverse isotropic and
poroelastic osteon cylinder considering Haversian fluid pressure.
mond and Naili[5]
modeled an osteon, a basic unit
of cortical bone, as a hollow cylinder and solved the poroelastic problem of the osteon under
cyclic loading. Wang et al.
[6, 7, 8]
described the buckling and creep buckling of biologic bone in
the form of a cylindrical shell. Wu et al.
[9, 10, 11]
proposed a new model of transverse isotropic and
poroelastic osteon cylinder considering Haversian fluid pressure.
In this paper, both the interstitial fluid and solid matrix are regarded as compressible, because in the case of soft tissues the assumption of incompressible constituents is appropriate, while in the case of hard tissues the assumption of incompressible constituents is no longer reasonable [12] and the assumption of compressible is a good model for bone tissue experiments [13] . According to Cowin and Mehrabadi [14] , the stress levels in bone tissue calculated by the incompressible assumption are always greater than or equal to those calculated by the compressible assumption, so in order to get more realistic results, we regard both the interstitial fluid and the solid matrix as compressible. In all of the above models, the blood pressure oscillations in the Haverian canal were not considered, while Haversian systems contain the blood vessels and the pore pressure in the Haverian canal cannot exceed a pore pressure that would collapse the blood vessels present for any significant length of time [15] . When the blood pressure oscillation in the Haverian canal is taken into account, a new compressible transverse isotropic poroelastic osteon model under cyclic axial loading and blood pressure oscillation is proposed according to the poroelasticity theory, and the analytical solution of pore fluid pressure is obtained. The fluid in canaliculi is assumed to be incompressible, so on the basis of Navier-Stokes equations of incompressible fluid, we obtain the analytical solutions of fluid flow velocity and fluid shear stress. 2 Poroelastic model of osteon
Figure 1 is the osteon model established in a cylindrical coordinate system. As shown in Fig. 1, the osteon is modeled as an annular cylinder and both the Haverian canal and the canaliculi are filled with interstitial fluid, whereri androrepresent the inner and outer radii of the osteon, respectively.
The constitutive laws for the compressible transverse isotropic poroelastic osteon model can be written as follows [15] :
where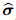 is the total stress vector for the entire medium,
is the total stress vector for the entire medium, 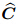 represents the drained elasticity
tensor,
represents the drained elasticity
tensor, 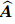 is called the Biot effective stress coefficient vector,
is called the Biot effective stress coefficient vector, 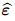 is the apparent strain tensor of
the solid matrix, Λ represents the reciprocal of Biot modulus, prepresents the interstitial fluid
pressure, and ζis the fluid content variation.
is the apparent strain tensor of
the solid matrix, Λ represents the reciprocal of Biot modulus, prepresents the interstitial fluid
pressure, and ζis the fluid content variation.
The only equation of equilibrium that is not satisfied automatically is
The conservation of mass for the fluid is
where k is the intrinsic Darcy law permeability, and μ is the fluid viscosity.
According to the actual physiological condition of bone, we consider the following boundary cases:
Atr=ri ,
Atr=ro,
According to Ref. [15], the interstitial fluid pressure solution can be described as follows:
where
Here, In and Kn are the first kind and the second kind modified Bessel functions of order n, respectively, ω stands for either ω or Ω, λ represents a dimensionless spatial variable, andα represents a specific value ofλ.The constantsA1ω , A1Ω , foω , andfoΩ can be obtained according to the boundary conditions. Their expressions are written as follows:
whereAccording to Ref. [15], the material properties and constants used in the calculations in this paper are given in Table 1.
 |
Figure 2 is the canaliculi model established in a cylindrical coordinate system, whereRis the radius of the canaliculi, and l (l=ro−ri ) is the length of the canaliculi.
 |
| Fig. 2 Model of interstitial fluid flow in canaliculi |
The movement of interstitial fluid in canaliculi can be described by the Navier-Stokes equations. Because the dynamic loading bone subjected is low frequency in physiological state, the inertial terms and body force can be neglected. We regard the canaliculi as a straight tube penetrating the osteon and neglect the lacuna in the canaliculi. The Navier-Stokes equations can be described as follows:
where u is the fluid velocity vector, ρis the interstitial fluid density, and μ is the fluid viscosity. We assume that the fluid flow in canaliculi is axisymmetric, so the fluid velocity only has the velocityuin the z'-direction, and the interstitial fluid pressure in the canaliculi is the function of z' and t only. Therefore, the Navier-Stokes equations can be simplified as follows:Because the fluid flow in canaliculi is axisymmetric and there is no slip on the canaliculi wall, we have the following boundary conditions:
At r' =0,
At r' =R,
We assume that the fluid velocityuhave the following functional dependencies:
Substituting (7) into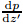 , we obtain the expression of
, we obtain the expression of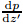 , which is assumed to take the form
where E andF are determined by the boundary conditions of osteon,
, which is assumed to take the form
where E andF are determined by the boundary conditions of osteon,
Substituting (22) and (23) into (19) yields
The solution to this equation is
whereSubstituting (26) into (20) leads to
Then, substituting (26) into (21), we obtainThe expression of the fluid velocityuis
From the formulation of fluid shear stress, we obtain that the fluid shear stress is
4 Results 4.1 Fluid flow velocity and fluid shear stress distributions along radial of canaliculiThe fluid flow velocity amplitude (u* =|u(r' , t)|) and fluid shear stress amplitude (τ* = |τ(r' , t)|) distributions versus the radius of canaliculi at the cross section of osteon inner wall are plotted in Fig. 3 and Fig. 4, respectively. As shown in Fig. 3, the fluid flow velocity amplitude decreases with the radius of canaliculi and the curve of fluid flow velocity amplitude versus the radius of canaliculi is a parabolic curve. The fluid flow velocity amplitude has the maximum at the center of canaliculi cross section, and it has the minimum at the canaliculi outer wall. Figure 4 shows that the fluid shear stress is proportional to the radius of canaliculi, and it has the maximum at the canaliculi outer wall.
 |
| Fig. 3 Fluid flow velocity distributions along radial direction of canaliculi |
 |
| Fig. 4 Fluid shear stress distributions along radial direction of canaliculi |
The maximum fluid flow velocity amplitude and fluid shear stress amplitude distributions versus radius of osteon are shown in Fig. 5 and Fig. 6, respectively. As shown in Figs. 5-6, the varying trends of the maximum fluid flow velocity amplitude and fluid shear stress amplitude distributions versus the radius of osteon are the same. Both the maximum fluid flow velocity amplitude and fluid shear stress amplitude decrease with the radius of osteon, and they reach the maximum at the osteon inner wall.
 |
| Fig. 5 Maximum fluid flow velocity distributions along radial of osteon |
 |
| Fig. 6 Maximum fluid shear stress distributions along radial of osteon |
Figure 7 presents the relationship between the maximum fluid flow velocity amplitude and the axial strain amplitude. Figure 8 presents the relationship between the maximum fluid shear stress amplitude and the axial strain amplitude. They are plotted at a constant loading frequency of 1 Hz and a constant blood pressure frequency of 1 Hz. The range of axial strain amplitude is 0.03%-0.5%. As shown in Figs. 7-8, both the fluid flow velocity and fluid shear stress increase linearly with the axial strain amplitude. When the axial strain amplitude varies from 0.03% to 0.5%, the fluid shear stress is from 7.95 Pa to 131 Pa at the osteon inner wall, so the axial strain amplitude has strong influence on the fluid shear stress.
 |
| Fig. 7 Maximum flow velocity amplitude as function of axial strain amplitude |
 |
| Fig. 8 Maximum shear stress amplitude as function of axial strain amplitude |
In order to study the influence of the other loading factor-axial loading frequency on fluid flow velocity amplitude and fluid shear stress amplitude, Figs. 9-10 are plotted with the axial loading strain amplitude fixed at 0.03% and blood pressure frequency fixed at 1 Hz. As shown in Figs. 9-10, the fluid flow velocity amplitude and fluid shear stress amplitude are proportional to the axial loading frequency. It also has strong effect on fluid flow velocity amplitude and fluid shear stress amplitude.
 |
| Fig. 9 Maximum flow velocity amplitude as function of axial loading frequency |
 |
| Fig. 10 Maximum shear stress amplitude as function of axial loading frequency |
The effect of permeability on the maximum fluid flow velocity amplitude and fluid shear stress amplitude are illustrated in Fig. 11 and Fig. 12, respectively. It is plotted atε0=0.03%, f=1 Hz, and f' =1 Hz. On the basis of Ref. [16], the range of permeability is between 10−24m2 to 10−18m2 . In this article we have chosen 10−22m2 as a reference and obtain the above results. As shown in Figs. 11-12, at the osteon inner wall the maximum fluid flow velocity amplitude and fluid shear stress amplitude decrease with the permeability, whereas at the middle of the osteon the maximum fluid flow velocity amplitude and fluid shear stress amplitude first increase with the permeability. When the permeability varies from 10−22m2 to 10−18m2 , the fluid flow velocity amplitude and fluid shear stress amplitude decrease with the permeability. From Figs. 11-12, we can see that the permeability can strongly affect the maximum fluid flow velocity amplitude and fluid shear stress amplitude.
 |
| Fig. 11 Maximum flow velocity amplitude as function of permeability |
 |
| Fig. 12 Maximum shear stress amplitude as function of permeability |
The aim of the work is to study the fluid flow velocity and fluid shear stress in canaliculi, a transverse isotropic saturated poroelasticity cylinder is modeled as an osteon with compressible constituents subjected to cyclic axial loading and blood pressure oscillations. In this model, the external loads and the internal blood pressure oscillations are taken into consideration, but there are idealized assumptions and simplifications in this model. The permeability is constant throughout the whole osteon in the model, and the influence of different microtubule system permeability on the whole model is ignored. The axial strain load is low frequency, period, and uniform.
We know that the micro-cracks also play an important role in the mechanotransduction of bone remodeling. In our paper, we assume the boundary condition of the outside boundary to be impermeable, and it represents normal bone tissue. When there are microcracks in osteon, interstitial fluid may flow out the osteon when the osteon is subjected to loading. The interstitial fluid flows from the high pressure to low pressure, besides, the direction of pressure gradient in interstitial fluid in different boundary condition is different. Thus, the interstitial fluid may flow from Haverian canal to canaliculi, or from canaliculi to Haverian canal. The interstitial fluid in Haverian canal contains considerable nutrients, and the nutrients with the interstitial fluid flow into canaliculi, which can provide bone cells with ample nutrients for bone remodelling. The flow of interstitial fluid can accelerate the exchange of nutrients between osteocytes and interstitial fluid, which can promote bone formation.
The fluid pressure distribution and interstitial fluid flow in osteon are more complex than we thought. The interstitial fluid flow direction may be multidimensional, and the fluid may not simply flow in or out the micro-tube system, whereas, it may also form seepage in microspace, and so on. Moreover, bone tissues have some electromechanical phenomenon in the result of fluid flow through the charged matrix [17] , and they play a very important role in bone remodelling. Thus, our future work is to research the streaming potentials generated by interstitial fluid flow. 6 Conclusions
The analytical solutions of fluid flow velocity and fluid shear stress in canaliculi to the problem of a transverse isotropic saturated poroelasticity cylinder modeling an osteon with compressible constituents subjected to cyclic axial loading and blood pressure oscillations are obtained and used to study variations in the fluid flow velocity and fluid shear stress. The results indicate that the fluid shear stress has the maximum at the osteon inner wall, and both the fluid flow velocity and fluid shear stress increase linearly with the axial strain amplitude and axial loading frequency. The permeability can strongly affect the maximum fluid flow velocity amplitude and fluid shear stress amplitude.
| [1] | Wolff, J. Das Gesetz der Transformation der Knochen. Hirschwald, Berlin, 8-12 (1892) |
| [2] | Biot, M. A. Theory of elasticity and consolidation for a porous anisotropic solid. Journal of Applied Physics, 26(2), 182-185 (1955) |
| [3] | Turner, C. H., Rho, J., Takano, Y., Tsui, T. Y., and Pharr, G. M. The elastic properties of trabecular and cortical bone tissues are similar: results from two microscopic measurement techniques. Journal of Biomechanics, 35(4), 437-441 (1999) |
| [4] | Abousleiman, Y. and Cui, L. Poroelastic solutions in transversely isotropic media for wellbore and cylinder. International Journal of Solids and Structures, 35, 4905-4929 (1998) |
| [5] | Rémond, A. and Naili, S. Transverse isotropic poroelastic osteon model under cyclic loading. Mechanics Research Communications, 32, 645-651 (2005) |
| [6] | Wang, F. and Wu, C. Q. Imitation bone optimization of composite pipe using trenchless technology. Journal of Mechanics and MEMS, 1(2), 311-315 (2009) |
| [7] | Yang, K. and Wang, F. Buckling of functionally graded cylindrically shells (in Chinese). Acta Scientiarum Naturalium Universitatis Sunyatseni, 47(2), 9-13 (2008) |
| [8] | Fang, F. and Wang, F. Creep buckling analysis of biologic bone in the form of cylindrical shell (in Chinese). Journal of North University of China (Natural Science Edition), 31(4), 364-368 (2010) |
| [9] | Wu, X. G., Chen, W. Y., Gao, Z. P., Guo, H. M., and Wang, L. L. The effects of Haversian fluid pressure and harmonic axial loading on the poroelastic behaviors of a single osteon. Science China Physics, Mechanics and Astronomy, 55, 1646-1656 (2012) |
| [10] | Wu, X. G., Chen, W. Y., and Wang, D. X. Mathematical osteon model for examining poroelastic behaviors. Applied Mathematics and Mechanics (English Edition), 34(4), 405-416 (2013) DOI 10.1007/s10483-013-1680-x |
| [11] | Wu, X. G. and Chen, W. Y. A hollow osteon model for examining its poroelastic behaviors: mathematically modeling an osteon with different boundary cases. European Journal of Mechanics-A/Solids, 40, 34-49 (2013) |
| [12] | Gailani, G. B. and Cowin, S. C. The unconfined compression of a poroelastic annular cylindrical disk. Mechanics of Materials, 40, 507-523 (2008) |
| [13] | Cowin, S. C. Bone poroelasticity. Journal of Biomechanics, 32, 218-238 (1999) |
| [14] | Cowin, S. C. and Mehrabadi, M. M. Compressible and incompressible constituents in anisotropic poroelasticity: the problem of unconfined compression of a disk. Journal of the Mechanics and Physics of Solids, 55, 161-193 (2007) |
| [15] | Cowin, S. C., Gailani, G., and Benalla, M. Hierarchical poroelasticity: movement of interstitial fluid between porosity levels in bones. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 367, 3401-3444 (2009) |
| [16] | Beno, T., Yoon, Y. J., Cowin, S. C., and Fritton, S. P. Estimation of bone permeability using accurate microstructural measurements. Journal of Biomechanics, 39(13), 2378-2387 (2006) |
| [17] | Lemaire, T., Lernout, C. E., Kaiser, J., Naili, S., Rohan, E., and Sansalone, V. A multiscale theoretical investigation of electric measurements in living bone. Bulletin of Mathematical Biology, 73(11), 2649-2677 (2011) |
 2015, Vol. 36
2015, Vol. 36



























