Shanghai University
Article Information
- Yuqi SHAN, Chao LIU, Maokang LUO. 2015.
- Simple analytical model for depth-averaged velocity in meandering compound channels
- Appl. Math. Mech. -Engl. Ed., 36(6): 707-718
- http://dx.doi.org/10.1007/s10483-015-1943-6
Article History
- Received 2014-5-14;
- in final form 2014-10-15
2. State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China;
3. College of Water Resource and Hydropower, Sichuan University, Chengdu 610065, China
A natural river often consists of a meandering main channel and two floodplains. When a flood occurs,the flow depth will increase,and the floodplains will be submerged,which may result in overbank flows in the meandering channels. The flow characteristics in a meandering compound channel are totally different from those in a straight compound channel. In the straight compound channel,the significant velocity difference between the main channel flow and the floodplain flow leads to a strong lateral shear stress in the mixing region. In the meandering compound channel,the flow under the bankfull level goes downstream in the meandering main channel,and the flood plain flow travels along the valley direction,which generates a strong vertical shear stress around the bankfull level in the main channel. The flow exchanges at the apex sections are weak,while the flow exchanges in the cross-over sections are significant. Besides,the velocities and the secondary flows,which are related to the sediment transports and bed forms,are longitudinally changing in the meandering channel. Therefore,for the engineering purpose,it is necessary to present a simple lateral distribution model (LDM) to accurately predict the depth-averaged velocity in a meandering compound channel.
Shiono and Muto[1] experimentally investigated the flow structures in the meandering compound channels with fixed beds and different sinuosities. To explore the differences between mobile cases and fixed cases,Shiono et al.[2] and Spooner[3] conducted a series of experiments to discuss the flow patterns. Shiono et al.[4] investigated the meandering compound channels with mobile beds and different floodplain conditions,and showed that the flow characteristics in the meandering compound channels were much more complicated than those in the straight compound channels. The flood plain flow contributed a lot to secondary flows,which resulted in the growth and decay of the secondary currents along the meander. Strong vertical shear stresses were caused due to the different flow directions of the main channel flow and the upper layer flow. The flow contraction and expansion were seen at the cross-over sections,which would affect the internal flow structure in the main channel. All these phenomena are specific characteristics of the meandering channel flow. Therefore,the discharge prediction in meandering compound channels is a challenge. Many methods have been proposed to predict the stagedischarge curve[5, 6, 7, 8, 9, 10]. Morvan et al.[11],Shao et al.[12],Zarrati et al.[13],Guo et al.[14],and Jing et al.[15, 16] proposed some two-dimensional (2D) and three-dimensional (3D) numerical models. Ervine et al.[17],McGahey and Samuels[18],and Huai et al.[19] proposed 2D analytical models to predict the depth-averaged velocities in meandering main channels based on the method of Shiono and Knight[20]. However,all these models use vertical coordinates,and calibrate the secondary flow parameter. More importantly,the analytical solutions in these models are very complicated,and are not appliable. Therefore,it is necessary to propose a simple but applicable method for the prediction of the depth-averaged velocity in a meandering compound channel.
This paper presents a simple analytical method with curvilinear coordinates to predict the depth-averaged velocities in the meandering compound channel. The governing equation is derived from the streamwise momentum equation and the flow continuity equation under the condition of quasi-uniform flow. The simple analytical solution is presented with the velocity parameter which contains the longitudinal velocity variation and the lateral velocity variation, and the predictive capability of this model is verified by the experimental data from different sources. Finally,the determination of the velocity parameter and the limitation of the proposed model are discussed.
2 Experimental arrangementsThree groups of experiments (MN1,MN2,and MN3) are conducted in a 35 m long,4 m wide, and 1 m high flume at the State Key Laboratory of Hydraulics and Mountain River Engineering (SKLH),Sichuan University,China. The 3D velocities at the two apex cross sections CS1 and CS7 (see Fig. 1),are recorded by the three-component Sontek Acoustic Doppler Velocimeter (ADV) equipped with up-side and down-side probes. At each point,the measurement period and frequency are set as 30 s and 50 Hz,respectively.
The shape of the meandering main channel is rectangular (see Fig. 2). The sinuosity (s) is designed as 1.381. The total width (B) and the main channel width (b) are 4.0 m and 0.7 m, respectively. The bankfull depth (h) is 0.14 m. Therefore,the aspect ratio (b/h) is 5. The inner radius (r) and the outer radius (R) are 0.9 m and 1.6 m,respectively. Therefore,the medium radius (Rm) is 1.25 m. The bed surface is smoothed and covered by a thin concrete layer. The flume has a fixed bed slope (S) of 0.001. The error in the geometry is controlled to be within 5%.
A summary of the experimental conditions is shown in Table 1,where Q is the discharge,H is the flow depth,Dr is the relative flow depth,and u∗ is the friction velocity. The parameters
 |
| Fig. 1. Plan details of geometry and measurement sections for meandering compound channel with curvilinear coordinates in main channel |
 |
| Fig. 2 Measurement vertical lines at CS7 in meandering main channel |

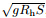 ,where g is the local gravitational acceleration,and Rh is the hydraulic radius. The
relative flow depth Dr is defined by
,where g is the local gravitational acceleration,and Rh is the hydraulic radius. The
relative flow depth Dr is defined by

The top view of the test meander is shown in Fig. 1. For this channel,the original point of the curvilinear coordinates at CS7 is set at the left-hand wall of the meandering main channel (see Fig. 2). This figure shows 13 vertical measurement lines denoted by 1 to 13 at CS1 and CS7 with a 0.05 m lateral interval from the left (y = 0.0 m) to the right (y = 0.7 m). The measurement intervals between two vertical points are arranged as 0.015 m. All experimental data are recorded under the quasi-uniform flow condition by ensuring that the water surface slope remained to be parallel to the bed slope at each meander by manually adjusting the downstream tailgate. When the deviation of the water surface and the bed slope is less than 5%,the quasi-uniform flow condition is considered to be attained,and the measurements are started.
This model is derived from the momentum equation with the curvilinear coordinates presented by Schlichting[21]. Under this curvilinear coordinates,the x-axis is parallel to the main channel ridge,and the y-axis is normal to the meandering main channel (see Fig. 1). The original point at CS7 locates at the corner next to the left floodplain (see Fig. 2). For the quasiuniform flow condition in the meandering compound channel,the momentum equation and the flow continuity equation with curvilinear coordinates may be shown as follows.
The momentum equation is
The continuity equation is
In the above equations,r is the radius of the curvature to the inside of the bend,x,y,and z are the streamwise,lateral,and vertical directions,respectively. U,V ,and W are the velocity components corresponding to the x-,y-,and z-directions,respectively. ρ is the flow density. τ xx,τyx,and τzx are the Reynolds stresses.Combining Eqs.(1) and (2) yields
Since  and
and  have the same dimension,it is assumed that
have the same dimension,it is assumed that

The ratio of the transverse velocity to the longitudinal velocity (V/U) is used herein to
represent the intensity of the secondary flows in the main channel. At the apex sections,the
centrifugal force enhances the secondary flow significantly,i.e.,the range of V/U is from −0.43
to 0.37,whereas in the straight compound channel,the range of V/U is from −0.11 to −0.065[22]
(see Fig. 3). This suggests the importance of the centrifugal force to the secondary flow in the
meandering main channel. Liu et al.[23] showed that in the meandering main channel,the
measured transverse velocity (V ) consisted of two parts,i.e.,the original secondary current
cell (Vo),which was enhanced by the centrifugal force,and the component of the upstream
flood plain flow (V1),i.e.,V = (1 + k)Vo + V1. Moreover,the effect of the centrifugal force on
the secondary flows might be considered as  ,where k is a dimensionless coefficient to
reflect the relation of the centrifugal force and the secondary flow. At the apex sections,the
directions of the main channel flow and the flood plain flow seam parallel. Therefore,the angle
between them can be considered as zero. This indicates that the contribution of the upstream
flood plain flow to the secondary flows may be ignored,i.e.,V1 = 0.
,where k is a dimensionless coefficient to
reflect the relation of the centrifugal force and the secondary flow. At the apex sections,the
directions of the main channel flow and the flood plain flow seam parallel. Therefore,the angle
between them can be considered as zero. This indicates that the contribution of the upstream
flood plain flow to the secondary flows may be ignored,i.e.,V1 = 0.
 |
| Fig. 3 Vertical profiles of V/U at centerline in meandering compound channel with data described in Section 2 and straight compound channel with experimental data from Yang et al.[22] |
Only considering the effect of the centrifugal force at the apex,we can rewrite Eq. (3) as follows:
Integrating Eq. (4) over the local flow depth (H) with


At the apex sections (CS1 and CS7),the velocity parameter may be presented as follows:
Liu et al.[23] experimentally investigated the longitudinal distributions of the depth-averaged
velocity,and found that at the apex sections,the gradient of the streamwise velocities was small
enough to be ignored,i.e., ≈ 0. Therefore,Eq. (7) can be simplified as
≈ 0. Therefore,Eq. (7) can be simplified as
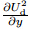 are separated,
and the five terms from the left to the right are labeled as “1” to “5”,respectively. Therefore,
Eq. (5) can be rewritten as follows:
where Term 1 is the velocity term,Term 2 is the gravity term,Term 3 and Term 5 are the
lateral shear stress terms,and Term 4 is the bed shear stress term.
are separated,
and the five terms from the left to the right are labeled as “1” to “5”,respectively. Therefore,
Eq. (5) can be rewritten as follows:
where Term 1 is the velocity term,Term 2 is the gravity term,Term 3 and Term 5 are the
lateral shear stress terms,and Term 4 is the bed shear stress term.
eral shear stress terms,and Term 4 is the bed shear stress term. To understand which term in Eq. (9) can be reasonably ignored,the experimental data in the case MN2 are taken as an example to show the quantity grade comparison of the five terms. The velocity term is unknown,which may be calculated a posteriori by the results of other four terms. All the parameters are shown in Table 1 except the dimensionless eddy viscosity which is a “catch all” parameter to describe the various 3D effects[20]. This parameter is 0.07 at the apex section in the meandering main channel,the same as that demonstrated by Liu et al.[23]. Therefore,the coefficients of Term 2,Term 3,Term 4,and Term 5 can be carried out. In Eq. (9),Term 2 (ρgHS) itself is a constant,i.e.,1.532. The coefficient in Term 3 is

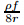 equals 3.972. Finally,the coefficient in Term
5 is
equals 3.972. Finally,the coefficient in Term
5 is

Based on the experimental velocity in the case MN2,it is possible to calculate the values of

The values of Φ for

To verify this finding further,six cases are used herein (see Table 2). For the study of Spooner[3],the experimental parameters are as follows:

The results of the six cases are shown in Table 2. From the table,we can see that the magnitude of Term 5 is much smaller than those of other four terms. Therefore,this term is first ignored. When Term 1,Term 2,Term 3,and Term 4 are compared,it is noticeable that in most cases,the magnitude of Term 3 is about ten times smaller than that of Term 4,and is much smaller than those of Term 1 and Term 2. Therefore,Term 3 is also ignored,and Eq. (9) may be rewritten as follows:
where Γmc(11) is a velocity parameter,but its value does not equal the value of Γmc in Eq. (9). In the following context,the subscript “mc(11)” of Γ indicates the velocity parameter in Eq. (11), while the subscript “mc” means the one defined in Eq. (9). In Eq. (11),the values of Φ of Term 2 and Term 4 are still 1.532 and 0.419,respectively. Though the value of Φ for the new term 1 (Γmc(11)) is changed to 1.113,the error reflected in the velocity parameter seems quite small, i.e.,
The analytical solution of Eq. (11) may be obtained as follows:
The velocity parameter (Γmc(11)) and the Darcy-Weisbach friction factor (f) are the only two control factors,which reflect the longitudinal and lateral velocity variations and the bed friction,respectively. The expression f = 8gn2 R1/3 h proposed by Knight et al.[24] and Huai et al.[25] was used to predict the friction factor in the main channel,where n is Manning’s coefficient.
The velocity parameters Γmc(11) and Γmc are calculated by Eqs. (9) and (11),respectively. Therefore,we can see the slight difference between Γmc(11) and Γmc due to the ignored contributions of Term 3 and Term 5. Apparently,Γmc(11) and Γmc are lateral variables,and are not easy for practical applications. For the convenience of applications,the averaged values of Γmc(11) and Γmc,i.e.,Γmc(11a) and Γmc(a),are used,and the effect of their differences on the predictions will be discussed later.
4 ApplicationsFour cases with different flow depths and river conditions are selected here to verify the predictive capability of the proposed model in the meandering compound channel. The experimental data of MN2 and MN3 are recorded in a large-scale channel (B = 4 m) with S = 0.001, and the details of the experimental parameters are shown in Section 2. The relative flow depth (Dr) is 0.35 for MN2,and is 0.25 for MN3. The measurements of g4_7 and g4_10 by Spooner[3] are taken in a relatively small channel with the width of 2.4 m and S = 0.002. The details of the flow parameters are introduced in the foregoing section. The values of Dr in g4_7 and g4_10 are 0.3 and 0.45,respectively. The values of s in Ref. [3] and our experiments are 1.384 and 1.381,respectively,which are almost identical.
Figure 4 shows all the experimental data and predictions. From this figure,we can see that the predictions in the meandering main channel with different hydraulic conditions agree well with four groups of experimental data,i.e.,MN2,MN3,g4_7 and g4_10. To show the accuracy of this model,the averaged absolute relative error (Ψr) is defined as follows:
where (Ud)calculated is the calculated depth-averaged velocity,(Ud)measured is the measured depth-averaged velocity,and N is the number of the measured depth-averaged velocity for each case. |
| Fig. 4. Comparison of predictive and experimental depth-averaged velocities in meandering main channel based on experimental data from Spooner[3] and our experiments |
Table 3 shows the values of Γ mc(11a) and Γmc(a) and the values of their corresponding Ψr in four cases,where percentages in the parentheses are the values of the averaged absolute relative error (Ψr). From the table,we can see that the difference between Γmc(11a) and Γmc(a) is quite small,which suggests the unimportance of two shear stress terms in Eq. (9),and demonstrates that the assumption of ignoring these two terms is reasonable. In all the cases,the predictions with Γ mc(11a) and Γmc(a) seem almost identical due to the nearly same values of Ψr. For all cases,the values of Ψr are always small,and the largest Ψr is only 4.68% in g4 7,indicating the good capability of this model in predicting the depth-averaged velocity in the meandering main channel. Although the values of Γmc(11a) and Γmc(a) are a little different,the depthaveraged velocities obtained with Γmc(11a) are still good enough to meet the practical purpose in engineering requirements.
In the foregoing section,we demonstrated that two shear stress terms are small enough to be ignored in Eq.(9),and the back calculations show that the values of Γmc(11a) and mc(a) are approximately identical. In this section,the determination of Γmc(11a) will be discussed in detail.
Based on the experimental data from Spooner[3] and this paper,the values of mc(11a) are back calculated. The results are shown in Fig. 5. From the figure,we can see that Γmc(11a) can be described as a second-order function of Dr. Therefore,in both channels,the relations shown in Fig. 5 may be used to predict mc(11a) at other flow depths,and thus the predictive depth-averaged velocities can be obtained. If only the lateral distribution of the depth-averaged velocity is known in a new meandering channel,Eq.(11) can be used to back calculate Γmc(11), and the corresponding Γmc(11a) can be obtained. Then,the relation between Γmc(11a) and Dr can be obtained. Once this has been done,this model can predict the lateral distribution of the depth-averaged velocity at other flow depths for the same geometric and hydraulic condition.
 |
| Fig. 5. Relation between Γmc(11a) and Dr based on experimental data from Ref. [3] and ours |
It is worth noting the limitation of the proposed model. Since this method is derived from the momentum equation and the flow continuity equation under the quasi-uniform flow condition, it is necessary to investigate its feasibility under other flow conditions. In the meandering compound channel,the growth and decay of the secondary flows in the meandering main channel are quite complicated,particularly at the cross-over sections,where the generation mechanism of the secondary flows is different from that at the apex section[23]. Therefore,this method is only suitable for predicting the depth-averaged velocity at the apex sections. In addition,in some cases,we cannot obtain the lateral distribution of the depth-averaged velocity. Therefore, the calibration may be a method to determine the value of Γmc(11a).
6 Conclusions
Three groups of experiments are conducted in a large scale meandering compound channel with smooth floodplains. The detailed velocity components are obtained at the apex sections. In the meandering main channel,the depth-averaged governing equation with curvilinear coordinates is derived from the momentum equation and the flow continuity equation under the quasi-uniform flow condition. According to the magnitude analysis of the five terms in Eq. (9), two lateral shear stress terms are ignored due to their minor contributions. Then,a simple but applicable model is obtained,and its analytical solution with a simple structure is presented. The predictive depth-averaged velocity is obtained when the lateral location is given. Four groups of experimental data from different sources are selected to verify the capability of this model for predicting the depth-averaged velocity in the meandering main channel. The predictions with the velocity parameters (Γmc(11a) and Γmc(a)) are almost identical. The averaged absolute relative error (Ψr) is presented to evaluate the predictive accuracy of this model,and the obtained values of Ψr in all cases are low,which demonstrates that the proposed model has a good predictive capability. The determination of Γmc(11a) is crucial for the practical application in a new meandering channel,and the initial calibration of the relation of Γmc(11a) and Dr is required. The results show that,this simple model can predict the depth-averaged velocity at other flow depths with the same geometry. However,this model is only suitable at the apex sections in the meandering compound channel under the quasi-uniform flow condition.
| [1] | Shiono, K. and Muto, Y. Complex flow mechanisms in compound meandering channel for overbank flow. Journal of Fluid Mechanics, 376, 221-261 (1998) |
| [2] | Shiono, K., Spooner, J., Chan, T. L., Rameshwaran, P., and Chandler, J. H. Flow characteristics in meandering channels with non-mobile and mobile beds for overbank flows. Journal of Hydraulic Research, 46, 113-132 (2008) |
| [3] | Spooner, J. Flow Structures in a Compound Meandering Channel with Flat and Natural Bedforms, Ph. D. dissertation, Loughborough University, U. K. (2001) |
| [4] | Shiono, K., Chan, T. L., Spooner, J., Rameshwaran, P., and Chandler, J. H. The effect of floodplain roughness on flow structures, bedforms and sediment transport rates in meandering channels with overbank flows: part I. Journal of Hydraulic Research, 47, 5-19 (2009) |
| [5] | Greenhill, R. K. and Sellin, R. H. J. Development of a simple method to predict discharges in compound meandering channels. Proceedings of the ICE-Water Maritime and Energy, 101, 37-44 (1993) |
| [6] | Lambert, M. F. and Sellin, R. H. J. Velocity distribution in a large-scale model of a doubly meandering compound river channel. Proceedings of the ICE-Water Maritime and Energy, 118, 10-20 (1966) |
| [7] | Shiono, K., Al-Romaih, J. S., and Knight, D. W. Stage-discharge assessment in compound meandering channels. Journal of Hydraulic Engineering, 125, 66-77 (1999) |
| [8] | Patra, K. C. and Kar, S. K. Flow interaction of meandering river with floodplains. Journal of Hydraulic Engineering, 126, 593-604 (2000) |
| [9] | Patra, K. C., Kar, S. K., and Bhattacharya, A. K. Flow and velocity distribution in meandering compound channels. Journal of Hydraulic Engineering, 130, 398-411 (2004) |
| [10] | Khatua, K. K., Patra, K. C., and Mohanty, P. K. Stage-discharge prediction for straight and smooth compound channels with wide floodplains. Journal of Hydraulic Engineering, 138, 93-99 (2011) |
| [11] | Morvan, H., Pender, G., Wright, N., and Ervine, D. A. Three-dimensional hydrodynamics of meandering compound channels. Journal of Hydraulic Engineering, 128, 674-682 (2002) |
| [12] | Shao, X. J., Wang, H., and Chen, Z. Numerical modeling of turbulent flow in curved channels of compound cross-section. Advances in Water Resources, 26, 525-539 (2003) |
| [13] | Zarrati, A. R., Tamai, N., and Jin, Y. C. Mathematical modeling of meandering channels with a generalized depth averaged model. Journal of Hydraulic Engineering, 131, 467-475 (2005) |
| [14] | Guo, Y., Zhang, L., Shen, Y., and Zhang, J. Modeling study of free overfall in a rectangular channel with strip roughness. Journal of Hydraulic Engineering, 134, 664-667 (2008) |
| [15] | Jing, H., Guo, Y., Li, C., and Zhang, J. Three-dimensional numerical simulation of compound meandering open channel flow by the Reynolds stress model. International Journal for Numerical Methods in Fluids, 59, 927-943 (2009) |
| [16] | Jing, H., Li, C., Guo, Y., and Xu, W. Numerical simulation of turbulent flows in trapezoidal meandering compound open channels. International Journal for Numerical Methods in Fluids, 65, 1071-1083 (2011) |
| [17] | Ervine, D. A., Willetts, B. B., Sellin, R. H. J., and Lorena, M. Factors affecting conveyance in meandering compound flows. Journal of Hydraulic Engineering, 119, 1383-1399 (1993) |
| [18] | McGahey, C. and Samuels, P. G. Methodology for conveyance estimation in two-stage straight, skewed and meandering channels. Proceedings of the XXX Congress of the International Association for Hydraulic Research, Thessaloniki, Greece, 33-40 (2003) |
| [19] | Huai, W. X., Gao, M., Zeng, Y. H., and Li, D. Two-dimensional analytical solution for compound channel flows with vegetated floodplain. Applied Mathematics and Mechanics (English Edition), 30(9), 1049-1056 (2009) DOI 10.1007/s10483-009-0906-z |
| [20] | Shiono, K. and Knight, D. W. Turbulent open channel flows with variable depth across the channel. Journal of Fluid Mechanics, 222, 617-646 (1991) |
| [21] | Schlichting, H. Boundary-Layer Theory, Springer-Verlag, Berlin (1968) |
| [22] | Yang, K. J., Cao, S. Y., and Knight, D. W. Flow patterns in compound channels with vegetated floodplains. Journal of Hydraulic Engineering, 133, 148-159 (2007) |
| [23] | Liu, C., Wright, N., Liu, X. N., and Yang, K. J. An analytical model for lateral depth-averaged velocity distributions along a meander in curved compound channels. Advances in Water Resources, 74, 26-43 (2014) |
| [24] | Knight, D. W., Omran, M., and Tang, X. Modeling depth-averaged velocity and boundary shear in trapezoidal channels with secondary flows. Journal of Hydraulic Engineering, 133, 39-47 (2007) |
| [25] | Huai, W. X., Xu, Z. G., Yang, Z. H., and Zeng, Y. H. Two dimensional analytical solution for a partially vegetated compound channel flow. Applied Mathematics and Mechanics (English Edition), 29(8), 1077-1084 (2008) DOI 10.1007/s10483-008-0811-y |
 2015, Vol. 36
2015, Vol. 36


















