1 Introduction

As a kind of important engineering structure,pipelines are widely used in petrochemical, nuclear power,heat exchange,and marine equipment applications. A pipeline conveying fluid is a simple and typical system which consists of two major sections,i.e.,the external tube and the fluid in it,and contains a wealth of dynamical phenomena mainly determined by the pipe parameters,the fluid parameters,and the external constraints. Moreover,pipes are used not only in transporting unidirectional flows such as gas,liquid,and solid but also in conveying multiphase flows such as gas-liquid,gas-solid,and liquid-solid flow^[1]. The responses and stability of piping system usually vary with respect to a number of factors which can be extremely complicated,of which the main factors are the fluid quality per unit,the fluid velocity,the pulse amplitude and so on,and many studies have been conducted to address these aspects^[2].

The dynamics of pipe conveying fluid was first studied by Ashley and Haviland,who tried to describe the vibration in the Tran-Arabian pipeline^[3]. Then,the dynamics of pipes has been widely studied by some other scholars,e.g.,Housner^[4] and Benjamin^[5]. Benjamin was the first researcher who studied the dynamics of tubes containing flowing fluid with one end free,and he was also the first person who observed that the dynamical problem is independent of the effects of the fluid friction^{[5, 6]}. Gregory and P¨ aidoussis^{[7, 8]} studied this problem further,identifying that for a sufficiently high flow velocity,the pipe system was subject to the flexural oscillatory instability,where the motion was confined in a horizontal plane.

During the subsequent thirty years,numerous studies on both the plain pipe and its variants were conducted,and the nonlinear dynamics and the chaotic dynamics of various cantilevered systems have been widely studied^[9]. P¨ aidoussis et al.^[10] studied a cantilevered pipe theoretically and experimentally,and discovered the dynamic characteristics of the system. They discovered that bifurcation and chaotic motion were under nonlinear motion-limiting constraints and steady flow. Li and P¨ aidoussis^[11] established the nonlinear equations of motion of a “standing” cantilevered pipe by the perturbation technique and Galerkin’s method,and analyzed the doubly degenerate case and the dynamical phenomena under different parameters. Jin^[12] investigated the cantilevered pipe conveying fluid with motion-limiting constraints and utilizing an elastic support,and obtained the instability regions of the system under different spring constants. Recent works on the dynamics of cantilevered pipe conveying fluid can be traced to the works of Wadham-Gagnon et al.^[13],and Modarres-Sadeghi et al.^[14],and Modarres-Sadeghi and P¨ aidoussis^[15]. The dynamics of cantilevered pipe conveying fluid has been studied quite extensively by many investigators. Significant results have been achieved^{[16, 17, 18, 19, 20, 21]}.

ensively by many investigators. Significant results have been achieved^{[16, 17, 18, 19, 20, 21]}. Nowadays,the economic prosperity has contributed to the development and erection of a variety of pipes,and the piping systems have become increasingly larger. In a very large system, the pipelines cannot all be placed horizontally or vertically,and are inevitably erected at inclined angles for various reasons such as material,space,and power supply. Therefore,the study of inclined pipe systems is imperative. P¨ aidoussis^[22] investigated the linear standing system (SS) and hanging system (H-S),and obtained the effects of the gravity factors on the stability of the systems. Wang and Ni^[23] studied nonlinear piping systems with elastic support and motion-limiting constraints,and analyzed the effects of the gravity parameter on the responses of the systems. However,both of these studies have not placed necessary attention on inclined systems and the effects of the supported angle on the stability and dynamic characteristics of the systems. It should also be noted that most of the scholars have not studied the related issues,which makes the current research on this subject necessary.

To compensate for the lack of ongoing research as mentioned above,the present paper is aimed at studying the effects of the supported angle on the stability and dynamical bifurcations of a cantilevered pipe conveying fluid,which,to our knowledge,has never been previously examined. In Section II,the equations of motion are determined through the stress analysis when the pipeline is erected in an inclined position. In Section III,the stabilities of two special systems,i.e.,the S-S and the H-S,are investigated based on the modal analysis. Section IV studies the effects of the supported angle on the characteristics of different systems,and presents the dynamical bifurcations with an increasing supported angle when the other parameters are fixed. In the final section,the results of this work are summarized and discussed^{[24, 25, 26]}.

2 Modeling of system

The considered system is shown in Fig. 1. As shown in the figure,it consists of a tubular cantilever with the length L,the internal perimeter S,the mass per unit length mp,the flexural rigidity EI,the conveying fluid mass per unit length mf,and the flowing axially velocity V . The cross-sectional flow area is A,and the fluid pressure is P. They are measured above the atmospheric level.

The pipe is hanging inclined. It is subject to the planar motion y(x,t). The axis of the pipe in its undeformed state coincides with the x-axis,which has a supported angle θ formed in the vertical direction. In the xy-plane,there are motion constraints,positioned at xb with a certain lateral clearance to the pipe and the linear spring support. The effect of the motion constraints and the spring support is defined as a restraining force defined by^{[27, 28]}:

where δ is the Dirac delta function,K₁ is the stiffness of the spring of the elastic support,and K₂ is the stiffness of the cubic spring representing the effect of the motion constraints.

2.1 Equations of lateral motion

Consider any one element,e.g.,δx,of the tube and of the enclosed fluid,subjected to the small lateral motion y(x,t) (see Fig. 2). The material of the pipe is viscoelastic,and consists of the Kelvin-Voigt type with a viscoelastic coefficient a. The internal fluid flow is steady and incompressible.

Since the diameter of the tube is small when it is compared with the wavelength of any disturbance to its center-line,the accelerations of the fluid particle in the x- and y-directions are zero and

respectively. The friction generated by the fluid is qS per unit length,where q is defined as the shear stress on the internal surface of the pipe. The transverse force between the tube and the fluid per unit length is F. The acceleration due to the gravity is defined as g. The supported angle between the axis of the tube and the vertical direction is defined as θ.

Neglecting the terms of the second-order and higher order of magnitude according to the Euler beam approximation for small lateral motion,from the force balances in the x- and y-directions concluded from the fluid element,we have

Similarly,as shown in the tube element,Q is the transverse force of the shear in the tube, M is the bending moment,and T is the axial tension of the pipe at the position x. From the tube element,we conclude that

Since the material is viscoelastic (the Kelvin-Voigt type),the stress-strain relationship can be written as

where E^∗ is the dissipation factor of the pipe’s material,and it can be written as E^∗ = aE.

Subtracting Eq.(5) to Eq.(3) to eliminate F and qS(),from Eq.(7),we have

Adding Eqs.(2) and (4),we have

Assume that the pipe suffers from the axial force T₀,and the fluid unit suffers from the force P A expressed by

at x = L. Then,integrating Eq.(9) from x to L,we have

In the above equations,P0 represents the pressure of the fluid at the end of the pipe. υ is Poisson’s ratio. δ is equal to 1 when the endpoint of the pipe is axially limited,while is equal to 0 when the endpoint is free. Here,we let δ and T₀ be equal to zero because of the free endpoint.

Substituting Eq.(10) into Eq.(9) and considering the external constraints as given by Eq.(1), we have

Introduce the following dimensionless variables and parameters^{[12, 29]}:

Substituting the above terms into Eq.(11),we have

According to the boundary conditions applied to the cantilevered pipe,the small lateral motion of the tube must satisfy

Apart from the support conditions,the characteristics of the tube,and the fluid mentioned in Ref.^[12],from Eq.(12),we can see that changing the supported angle will bring additional items by the gravity parameter.

2.2 Discrete equations of motion

In order to facilitate the solution of the above differential equation,we discretize Eq.(12) by Galerkin’s method,and transform the partial differential equation to ordinary differential equations. Let

where

In the above equations,ϕ_r(ζ) is the eigenfunction of the cantilevered beam in dimensionless form,q_r(τ) is the displacement function of τ,and η(ζ,τ) is the response function of the system which is expressed by the superposition of the infinite set of the normal modes of the cantilever.

According to Ref. ^[12],a high accuracy can be achieved when the two-mode expansion (N = 2) in Eq. (14) is adopted in the analytical model. To facilitate the analysis,we write the equation in the matrix form,i.e.,

where

Substituting Eq. (15) into Eq. (12) and multiplying the vector Φ by the left,we have

where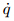 and 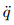are the derivatives of q with respect to τ,Φ',Φ",and Φ₍₄₎ are the derivatives of Φ with respect to ζ.

Integrating the above equation in the interval ^{[0, 1]} with respect to ζ and using the orthogonality of the modes,we obtain

where

and λ_r (r = 1,2) are the eigenvalues of the cantilever beam.

3 Modal analysis on vibration of H-S and S-S

Through the above analysis of the formula,we can see that the dynamical equation (17) of the system will change when the supported angle θ changes and the system may then exhibit different features. Here,we consider two special cases,i.e.,θ = 0° and θ = 180°. According to Eq. (17),we have

Then,Eq. (17) can be changed to

These are special cases that often occur in reality since pipelines are often erected vertically. Through the analysis of the coefficient matrix of the equation,we can obtain the response q of the system. If we denote Im (ω_r) as the imaginary part and Re (ω_r) as the real part of ω_r (r = 1,2) (see Eq. (14)),then the motion of the system will have the following characteristics:

(i) When Im (ω_r) = 0,the response frequency of the pipeline system conveying fluid is zero. Under this condition,if Re (ω_r) is negative,then the system is in a statically stable state. If Re (ω_r) is positive,then the system is in a statically divergence unstable state. If Re (ω_r) is also equal to zero,then the system is in a critical state between the two states mentioned above.

(ii) When Im (ω_r) is positive,the motion frequency is greater than zero. In this case,if Re (ω_r) is negative,then the vibration magnitude of the system will gradually decay,and the system finally reaches the dynamic steady state. If Re (ω_r) is positive,then the vibration magnitude of the system will oscillate,and the system will be in a flutter unstable state. If Re (ω_r) is equal to zero,then the system will keep its amplitude and never stop vibrating. In this case,the system is in the critical state between the dynamic steady state and the flutter unstable state,and the supported angle θ is called the critical supported angle.

The linear system and the effects of the parameters β and g on the responses of the system have been investigated in Ref. ^[22],where the viscoelastic coefficient a is equal to zero and the system has no spring support or external constraints,i.e.,

According to Ref. ^[23],when the spring support and the external constraints are added,we can make the diagram of the former two modes of the system with different parameters. In order to have a better perspective on the effects of the parameters on the system,we change just one parameter at each time,and keep the others unchanged. The results are shown in Fig. 3. From this figure,we can see the changing trends of the former first-response and the second-response of the H-S (θ = 0°) and S-S (θ = 180°) with different parameters,and speculate that the effects of the parameters on the system cannot be neglected.

We let^{[22, 23]}

in Fig. 3(a) to obtain the reference data. From Fig. 3(a),we can see that the first-order response frequencies of both the H-S and the S-S decrease when the flow rate increases. When the imaginary parts of the first-order mode and second-order mode of the H-S are greater than zero,they are always greater than those of the S-S under the same flow rate,which means that the H-S has a larger vibration frequency. In Fig. 3(b),we change the parameter k1 to 1,and obtain the response curves. From the figure,we can see that the trends of the curves are different from those of Fig. 3(a),and the first-order response of the S-S begins with a static buckled state, which means that the system is in a critical condition. In order to show the difference between Fig. 3(a) and Fig. 3(b),we let β be 0.5 in Fig. 3(c) and ζ_b be 0.5 in Fig. 3(d). From Figs. 3(c) and (d),we can see that the changing trends of the response curves are similar to those of Fig. 3(a). However,the response curves both have their own characteristics,especially in Fig. 3(d). As shown in Fig. 3(d),the first-order responses undergo attenuation,static buckling,attenuation, and static buckling when the flow rate increases. Päidoussis^[22] has not provided the test results under these types of conditions. In order to have a more global prospect for the effects of the parameters on the systems,we obtain the changing surfaces of the systems under different parameters through numerical methods,which is very different from what has been done in Refs. ^[22] and ^[23].

We know that pipeline may carry many things,such as gas,liquid,and solids. If the quality of the pipeline is kept unchanged,then the fluid mass per unit length will determine the mass ratio β of the system. According to Ref.^[23],here we let

and make β increase from 0 to 1. Similar to the above analysis,we get Fig. 4 which shows the real and imaginary changing trends of the responses of the H-S and the S-S.

As mentioned above,the mass ratio can range from 0 to 1 in theory because of different fluids. However,the values near the start point and the end point are hard to be achieved in real life. Therefore,here we just aim to observe the trend of the responses of the systems. Figure 4 shows the response of the changing surfaces at different mass ratios and velocity rates. From the figure,we can see that the changing surfaces of the S-S are similar to those of the H-S. When the mass ratio β is small,the first-order imaginary part decreases until zero when the dimensionless velocity increases. When β is larger,the imaginary part decreases in the previous section,and increases in the later section. The first-order real part surfaces have similar changing trends to the imaginary ones. However,all the values of the H-S are below the zero plane,while some values of the S-S are greater than zero. This means that the S-S will flutter and be unstable in this region. The second-order imaginary part surfaces of both the H-S and the S-S also decrease when the mass ratio is small,and decrease first and increase later when the mass ration is greater. The second-order real part surfaces are different from those of the first-order ones. When β is small,the second-order real part decreases first,and increases later. When β grows larger,the second-order real part surfaces keep decreasing. Moreover, both of the surfaces have their values greater than zero. According to the obtained surfaces, we can draw the critical line of the system (see Fig. 5).

The H-S has no critical line in the first-order mode. The critical line of the S-S shows that the critical velocity increases when the mass ratio β increases (see Fig. 5(a)). The system will be stable when the parameter is located on the right-side of the curve,but flutter and be unstable when it is located on the left-side of the curve. From Fig. 5(b),we can get the same trend of the curves as shown in Fig. 5(a). The critical velocity of the H-S is greater than that of the standing one when β is fixed. From the above study,we can conclude that the mass ratio can affect the stability of the system. The system always begins with a vibration state with a frequency close to zero. When the flow velocity increases,the system will reach a critical state first,and then flutter. Usually,the critical velocities will change when the mass ratio changes, and a larger mass ratio corresponds to a larger critical flow velocity,which means that we can keep the system stable through changing the parameter β.

Since the foundation and the supported means may be different in engineering applications, the supported position ζ_b and the linear spring stiffness k₁ will be different (see Fig. 1). When k₁ changes,we let

which are the same as those in Refs. ^[22] and ^[23] except k₁. In Fig. 6,we show the changing trends of the real and imaginary parts of the responses of the H-S and the S-S.

As shown in Fig. 6,the responses of the S-S are also similar to those of the H-S when k₁ changes. The first-order responses of the two systems are both stable because all the values of the real parts are smaller than zero,while the real part surfaces of the second-order responses both have intersecting lines with the zero plane. From Fig. 7,we can see that the system flutters in an unstable state when the parameters are in the area above the critical line,while is stable when the parameters are in the area below the critical line. Moreover,we can also see that the critical dimensionless velocity increases when the spring stiffness increases. The S-S has a smaller critical velocity than that of the H-S under the same k₁,which means that the S-S comes to the unstable state earlier when the velocity increases.

As mentioned above,the supported position ζ_b may also change under different conditions, which will also affect the response of the system. When ζ_b changes,we let

We make the supported position ζ_b range from 0.5 to 1 since we generally fix the pipeline at the latter half part. In Fig. 8,we show the changing trends of the two responses of the H-S and the S-S.

From Fig. 8,we can see that the surfaces of the H-S are similar to those of the S-S,and the first-order responses and the second-order responses of the two systems have the critical lines as shown in Fig. 9. The first-order responses of the systems are dynamically stable when the supported position ζ_b is located in the area to the left of the critical curves,i.e.,the area A is for the S-S,and the areas A and B are for the H-S. However,the system will flutter unstable in the area to the right of the critical curves,i.e.,the areas B and C are for the S-S and the areas C and D are for the H-S. When ζ_b changes with real applications,the S-S will undergo divergence instability at a lower dimensionless velocity,just as the previous ones show. From Fig. 9(b),we can see that the second-order mode critical lines also change with ζ_b,which are similar to those shown in Fig. 7. The pipe is stable in the area below the critical line,and flutters in the area above the line.

Through the above analysis,we can clearly see that the parameters β,k₁,and ζ_b have different effects on the responses of the H-S and the S-S with similar changing trends. According to the above figures,we can see that the second-order responses of the systems usually reach an unstable state earlier than the first-order responses,and the first-order responses have no critical lines and are sometimes dynamically stable. When the systems are in the same conditions,the S-S usually reaches the critical state first because of the gravity of the fluid and the pipe layout of the system. Moreover,the H-S is usually more stable than the S-S because of the supported condition.

4 Effects of supported angle on stability and bifurcations

In Ref. ^[23],it has been proved that the effects of the gravity parameter on the dynamic characteristics of the cantilevered pipe conveying fluid (see Fig. 1) cannot be neglected. In order to study the dynamic characteristics of this pipe at different supported angles,we let^{[22, 23]}

and the range of the supported angle be from 0° to 180°. There is a direct relationship between the parameter γ defined in Ref. ^[23] and the parameter ¯ g given in the present study,i.e.,

Since the parameter g is fixed,when θ = 0°,90°,and 180°,γ = 10,0,and −10,respectively,and the corresponding systems are called the H-S,the horizontal system,and the S-S, respectively. Here,we just define the dimensionless displacement Y by

By means of the numerical simulation,we get the bifurcation diagram of the cantilevered system conveying fluid at different supported angles. The results are shown in Fig. 10. It is shown that when the supported angle is equal to zero,i.e.,the H-S,the dimensionless displacement Y of the system keeps at zero from about 6.60 to 6.81,and no bulking occurs at the beginning of the flow (see Fig. 10(a)),then similar to Ref.^[23],a lower dimensionless fluid velocity v corresponding to the Hopf bifurcation is detected at vH,which is approximately equal to 6.80. When the dimensionless flow rate is smaller than vH,the vibration amplitude constantly decreases due to the damping effect,and eventually reaches a fixed value. If the flow rate is larger than vH,a limit cycle appears,and the system starts period-1 motion. Then, the period-doubling bifurcation appears at v_pd,which is approximately equal to 8.02. After that,the system undergoes period-2 motion. When the dimensionless velocity increases further,a sequence of period-doubling bifurcations emerge,and chaotic motion appears. Figure 10(b) shows the dynamic characteristics of the dimensionless displacement of the horizontal system when the supported angle is equal to 90◦. From this figure,we can see that the system is buckled,and the dimensionless displacement decreases from about 0.18 to 0.14 when the dimensionless velocity increases from 5.50 to 6.30,which is distinguished from the former one. The Hopf bifurcation appears at about 6.30,the period doubling bifurcation appears at about 7.56,and then the system ultimately undergoes the chaotic motion. Figure 10(c) shows the bifurcation diagram of the S-S,which is the same as that shown in Fig. 4 in Ref.^[23],and the dimensionless displacement has the similar changing trend as shown in Fig. 10(a) when the dimensionless velocity increases.

Combined with the three different values mentioned above,it is clear that the responses of the H-S and the S-S have changed with different supported angles. Therefore,the effects of the supported angle on the system flow cannot be neglected. Moreover,according to the figures, we can see that if the supported angle increases,the Hopf bifurcation and the period-doubling bifurcation appear at lower dimensionless velocities. Therefore,it can be inferred that a lower fluid velocity can induce chaotic motion when the supported angle is larger. In order to validate this phenomenon,we choose the values of the parameters as follows^[22]:

Figure 11 shows the bifurcation diagrams for the tip displacement of the pipeline system when

The results show that the dimensionless displacement Y of the system stays at zero,and no buckling phenomenon occurs at the beginning part of the horizontal axis (see Fig. 11 (a)) until the Hopf bifurcation appears. The values of Y keep positive,and decrease when v increases (see Fig. 11(b)). In Fig. 11(c),the dimensionless displacement keeps positive and decreases at the beginning,then turns negative and increases until zero,and finally keeps constant until the Hopf bifurcation appears. From Figs. 11(a)-11(c),we can see that the Hopf bifurcation appears when the values of v are 6.30,5.80,and 5.0 for the H-S (see Fig. 11(a)),the horizontal system (see Fig. 11(b)),and the S-S (see Fig. 11(c)),respectively. When the supported angle increases, the dimensionless velocity for the chaotic motion decreases too,just the same as that shown in Fig. 10.

To be more specific in reflecting the effects of the supported angle on the system,we keep the values of the parameters as follows:

By means of a numerical simulation,we obtain the relationship between the dimensionless amplitude and the supported angle (see Fig. 12). From the bifurcation diagram for the tip displacement of the cantilevered system,the system begins with period-1 motion. When θ increases,the period-doubling bifurcation occurs at θ_pd,which is approximately equal to 93°. Then,a series of period doubling bifurcation phenomena appear constantly,and the system undergoes the paroxysmal chaotic motion first and the chaotic motion finally.

This phenomenon is also reflected in the phase diagram shown in Fig. 13. It is worth mentioning that since all the parameters are fixed except the supported angle ranging from 0° to 180°,the system begins with period-1 motion instead of a buckling state under the conditions of these parameters,and the Hopf bifurcation that usually appears before the period-1 motion will not appear in this case. This makes the bifurcation diagram seem to have two parts.

In Fig. 13,we can see that when θ increases,the pipe system first undergoes symmetric limit cycle motion (flutter) (see Fig. 13(a)),then a period doubling bifurcation occurs,an asymmetric limit cycle arises,and the system undergoes period-2 motion (see Fig. 13(b)). As the supported angle θ increases further,a series of period-doubling bifurcations appear. When the number of bifurcations increases,chaotic motion emerges (see Figs. 13(c) and 13(d)). When the supported angle continues increasing,the system comes to a reversed bifurcation phenomenon,the chaotic motion disappears,period-5 motion emerges (see Fig. 13(e)),then the chaotic motion reappears (see Figs. 13(f)-13(h)),and finally the system undergoes the paroxysmal chaotic motion. When the support angle reaches about 145°,the system will be in a divergence state.

We try to modify the values of the parameters of the system to obtain the responses through a numerical method. The results show that the system has a bifurcation phenomenon when the supported angle increases with different parameters of the system. Figure 14 shows the bifurcation diagram for the tip displacement of the cantilevered system with different supported angles when v = 7.5,β = 0.2,α = 0.005,ζ_b = 0.82,g = 25,k₁ = 20,and k₂ = 100. The results show that the system begins with the motion of amplitude attenuation,then the Hopf bifurcation,the period-doubling bifurcation,the chaotic motion,and at last a divergence motion. Different from Fig. 12,the system is buckled when the supported angle is small,and no any paroxysmal chaos occurs. In Fig. 14,the points between 25° and 40° are thicker than those shown in Figs. 10-12 because of the motion characteristics of the system and the drawing method we use here. The figure is composed of a lot of points,which represent the displacement values of the pipe’s end when the corresponding velocities are zero at different time. As the system is autonomous and the numerical result is discrete,it is difficult to find when the speed values are exactly equal to zero. We regard the speeds less than a certain value as the zero solutions. When the supported angle is between 25° and 40°,the system vibration amplitudes increase slowly,and we begin to take the points after certain time. Therefore,the points seem thicker than those shown in Figs. 10-12.

From the above analysis,we can obtain that different velocity flow conditions will make the system have different dynamic characteristics and present different phenomena when the supported angle is fixed. When the velocity value is unchanged,different supported angles will also make the system have different dynamic features. Moreover,smaller velocity and smaller supported angle will make the system relatively stable. As the dimensionless velocity and the supported angle increase,the system will undergo a series of bifurcation processes,and show rich dynamic phenomena (see Fig. 12 and Fig. 14). No matter how it begins,the system will include the whole courses,i.e.,buckled bifurcation,Hopf bifurcation,period-doubling bifurcation,chaotic motion,and divergence motion,or parts of them. Therefore,as the pipe is erected,we should use appropriate parameters and adapt proper support conditions according to the specific circumstances. From Eq.(17),we can see that k2 is the nonlinear term,and has an assignable effect on the system.

5 Conclusion

Due to various environmental factors and limitations in actual production,pipe conveying fluids can be erected in different states. A variety of different conditions have been investigated by scholars all around the world. However,the effects of the supported angle on the pipe’s dynamics have seldom been studied.

Through the force balance and the stress-strain relationship,we have derived the partial differential equation of the pipe,which is discretized by Galerkin’s method. By means of the modal analysis,we find that the responses of the S-S and the H-S are very similar and have an analogous changing trend. Moreover,the second-order responses reach the critical state first,and become unstable earlier than the first-order responses. Sometimes,the first-order responses have no critical values,and stay dynamically stable over the entire the range. When the supported conditions are the same,the S-S is easier to reach the critical value than the H-S because of the effect of gravity on the pipe.

The H-S,horizontal system,and S-S have different bifurcation diagrams and perform differently when the supported angle is fixed and the velocity changes. When the dimensionless velocity stays unchanged,the system also has a bifurcation phenomenon when the supported angle changes,and it is very common when other parameters change. Usually,the system will undergo the buckling,Hopf bifurcation,period-doubling bifurcation,chaotic motion,and divergence instability motion or parts of them. Sometimes,reversed bifurcation may occur,and the system may undergo paroxysmal chaotic motion. The system sometimes is very sensitive to the supported angle within a certain range,and a small change of the supported angle will cause the system’s responses to mutate.

As the pipeline systems are becoming increasingly larger nowadays,the inclined pipe exists because of its special conditions,and it is therefore worthy being concerned about. Through an analysis,we learn that the supported angle can determine the stability and dynamical characteristics of the system,and has a better prospect which helps to guide us to a better application for pipelines. However,as we know,pipelines have a variety of supported applications,such as simply supported or clamped supported at both ends and one end simply supported and the other clamped,the fluid in it may be steady or pulsating. The problems of whether the supported angle has effects on the system or not and how it might affect the system’s principal parameters and the internal resonances have not been investigated. In this connection,further studies are warranted.