Shanghai University
Article Information
- T. HAYAT, T. MUHAMMAD, S. A. SHEHZAD, A. ALSAEDI. 2015.
- Three-dimensional boundary layer flow of Maxwell nanofluid: mathematical model
- Appl. Math. Mech. -Engl. Ed., 36(6): 747-762
- http://dx.doi.org/10.1007/s10483-015-1948-6
Article History
- Received 2014-7-20;
- in final form 2014-10-23
2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia;
3. Department of Mathematics, Comsats Institute of Information Technology, Sahiwal 57000, Pakistan
A mixture of nanoparticles and a base fluid is known as a nanofluid. Nanofluids are useful in several engineering and industrial applications due to their extraordinary thermal conductivity. The colling rate of ordinary heat transfer fluids is very low because such fluids have lower thermal conductivity. The thermal conductivity and thermal performance of ordinary heat transfer fluids can be enhanced if nanoparticles are submerged in the fluids. Such novel properties of nanofluids make them potentially applicable in various processes of heat transfer such as microelectronics,fuel cells,and hybrid-powered engines.
Masuda et al.[1] examined the variations in the thermal conductivities and viscosities of liquids through the dispersion of ultra-fine particles in the base fluids. Choi and Eastman[2] showed that the presence of nanoparticles in the base fluid could enhance the thermal properties of the fluid. Buongiorno[3] developed a mathematical model to explore the thermal properties of the base fluid,in which the Brownian motion and thermophoresis were utilized to enhance the thermal properties of the base liquid. Khan and Pop[4] investigated the two-dimensional flow of the nanofluid over a linear stretching sheet,developed the numerical solutions of the modeled differential system through the Keller-box method,and provided a detailed analysis of the Brownian motion and thermophoresis effects on the heat transfer characteristics. Turkyilmazoglu[5] analyzed the heat and mass transfer effects in the hydromagnetic flow of a viscous fluid with the slip conditions and various types of nanoparticles including Cu,Ag, CuO,Al2O3,and TiO2. Makinde et al.[6] explored the buoyancy driven flow caused due to the convectively heated stretching/shrinking sheet of the magneto nanofluid near a stagnation point,and discussed the simultaneous effects of the buoyancy force,convective heating, thermophoresis,and applied magnetic filed with the Runge-Kutta fourth-order scheme of the shooting technique. Rashidi et al.[7] investigated the entropy generation analysis in the steady magnetohydrodynamic (MHD) flow due to a rotating porous disk in the nanofluid,and showed that this research was quite useful in rotating MHD energy generators for new space systems and thermal conversion mechanisms for nuclear propulsion space vehicles. Sheikholeslami and Ganji[8] analyzed the heat transfer effect in Cu-water nanofluid flow between parallel plates. Here,the effective thermal conductivity and viscosity of nanofluid were computed through the Maxwell-Garnetts and Brinkman models. Mustafa et al.[9] examined the numerical and series solutions for the stagnation point flow of the nanofluid over an exponentially stretching sheet, and concluded that both the thermal boundary layer thickness and the temperature enhanced remarkably when the Brownian motion increased. Kuznetsov and Nield[10] discussed the revised model of the natural convective boundary-layer flow of the nanofluid past a vertical plate,and showed that the nanofluid particle fraction on the boundary was passively rather than actively controlled.
The analysis of non-Newtonian fluids is a hot topic of research for recent investigators due to its numerous industrial and engineering applications. In particular,these fluids are encountered in bioengineering,chemical and nuclear industries,material processing,polymeric liquids,and foodstuffs. Several fluids such as shampoos,paints,paper pulp,ketchup,apple sauce,certain oils,and polymer solutions are the examples of non-Newtonian fluids. The characteristics of all the non-Newtonian fluids cannot be explained through one constitutive relationship. Thus, various models of non-Newtonian fluids have been proposed in the past.
ious models of non-Newtonian fluids have been proposed in the past. Generally,non-Newtonian fluids can be divided into three categories,i.e.,(i) differential type,(ii) rate type,and (iii) integral type. The Maxwell fluid model is the simplest subclass of rate type fluids. This model describes the characteristics of the relaxation time. Wang and Tan[11] explored the stability criteria of the Maxwell fluid model,where the fluid filled the porous medium,under the Soret-driven double diffusive convection. Fetecau et al.[12] gave the exact solution for the unidirectional flow of fractional Maxwell fluid model,where the flow was caused due to the coaxial rotation of the cylinders,with the Laplace and Hankel transforms to construct the exact solutions of the considered flow analysis. Hayat et al.[13] examined the two-dimensional boundary layer flow of the Maxwell fluid with convective boundary conditions and the suction/injection effects,and utilized the homotopy analysis method to compute the velocity and temperature expressions. Mukhopadhyay[14] analyzed the unsteady flow of the Maxwell fluid with heat generation/absorption,and showed that the fluid velocity decreased when the magnetic parameter increased,and an increase in the Maxwell parameter had the effects of suppressing the velocity field and increasing the temperature. Abel et al.[15] explored the MHD and the heat transfer effects in the flow of an upper convected Maxwell fluid over a porous shrinking sheet. Hayat et al.[16] reported the thermal radiation and thermal stratification effects in the mixed convection flow of the Maxwell fluid. Abbasbandy et al.[17] investigated the Falkner-Skan flow of the Maxwell fluid past a stretching surface. Shehzad et al.[18] investigated the effects of heat generation/absorption and variable thermal conditions on the MHD threedimensional flow of the Maxwell fluid.
The aim of the present analysis is to investigate the three-dimensional boundary layer flow of Maxwell nanofluid with heat source/sink and the newly introduced condition[10]. Such a condition is yet utilized only for the viscous fluid flow situation. Our interest here is to utilize such a condition in the theory of non-Newtonian fluids. Here,we prefer to utilize such a condition in the three-dimensional flow of Maxwell fluid. The resulting strong nonlinear problems are computed and analyzed through the series solutions by the homotopy analysis method (HAM)[19, 20, 21, 22, 23, 24, 25, 26, 27]. The effects of heat generation/absorption are also explored. The discussion of the plots and numerical values with respect to various parameters of interest is given.
2 Mathematical modelingWe consider the steady three-dimensional flow of an incompressible Maxwell nanofluid (see Fig. 1). The flow is caused by a linear stretching surface at z = 0. The flow occupies the domain z > 0. The effects of heat source/sink,Brownian motion and thermophoresis are taken into account. The thermophysical properties of fluid are taken to be constant. The constitutive equations for the flow of an incompressible Maxwell fluid are
 |
| Fig. 1. Sketch of problem |
The Cauchy stress tensor T and the extra stress tensor S are defined as follows:
where D/Dt is the covariant differentiation,and λ1 is the relaxation time. The first RivlinEricksen tensor A1 is defined as follows: where * indicates the matrix transpose,and the velocity field V is given by The definition of D/Dt is[27] With the theory in Ref. [28] and the boundary layer assumptions in Ref. [29],the governing boundary layer expressions in the Maxwell fluid[18, 27] with heat and mass transfer can be expressed as follows: The boundary conditions for the present flow analysis are where u,v,and w are the velocity components in the x-,y-,and z-directions,respectively. ν is the kinematic viscosity defined by ν = μ/ρf,where μ is the dynamic viscosity. ρf is the density of the base fluid. T is the temperature. α = k/(ρc)f is the thermal diffusivity of the fluid. k is the thermal conductivity. (ρc)f is the heat capacity of the fluid. Q is the heat generation/absorption coefficient. (ρc)P is the effective heat capacity of nanoparticles. DB is the Brownian diffusion coefficient. C is the concentration. DT is the thermophoretic diffusion coefficient. Tw and T∞ are the temperatures of the surface and far away from the surface. C∞ is the concentration far away from the surface. The subscript w denotes the wall condition. Here,we assume that the surface stretching velocities and the wall temperature are where a,b,and T0 are positive constants.The dimensionless variables can be defined as
Then,we can obtain that Eq. (8) is automatically satisfied,and Eqs. (9)-(15) can be rewritten as follows: where β is the Deborah number,c is the ratio of stretching rates,Pr is the Prandtl number,S is the heat source/sink parameter,NB is the Brownian motion parameter,NT is the thermophoresis parameter,Le is the Lewis number,and prime stands for differentiation with respect to η. These parameters can be defined as follows: The local Nusselt number Nux is defined as The dimensionless mass flux represented by a Sherwood number Shx is now identically zero, and Rex = Uwx/ν is the local Reynolds number. 3 Solution computationThe initial guesses and the linear operators are
The above operators satisfy the properties given as follows: where Ci (i = 1,2,· · · ,10) elucidate the arbitrary constants.We can define the following zeroth-order deformation problems:
In the above expressions,p denotes the embedding parameter, f ,
f , g,
g, θ,and
θ,and  φ are the
non-zero auxiliary parameters,and
φ are the
non-zero auxiliary parameters,and 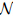 f ,
f , g,
g, θ,and
θ,and  φ are the nonlinear operators. Set
φ are the nonlinear operators. Set

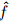 (η; p),
(η; p),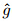 (η; p),
(η; p),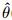 (η,p),and
(η,p),and  (η,p) vary from the initial guesses
f0(η),g0(η),θ0(η),and φ0(η) to the final solutions f(η),g(η),θ(η),and φ(η),respectively. The
Taylor series expansion gives
The convergence of Eqs. (41)-(44) strongly depends upon the suitable choices of
(η,p) vary from the initial guesses
f0(η),g0(η),θ0(η),and φ0(η) to the final solutions f(η),g(η),θ(η),and φ(η),respectively. The
Taylor series expansion gives
The convergence of Eqs. (41)-(44) strongly depends upon the suitable choices of  f ,
f , g,
g, θ,and
θ,and  φ. Since
φ. Since  f ,
f , g,
g, θ,and
θ,and  φ are chosen in such a manner that Eqs. (41)-(44) converge at p = 1,
The general expressions of the solutions can be expressed as follows:
where f∗m (η),g∗m (η),θ∗m (η),and φ∗m(η) are the special functions.
4 Convergence analysis
φ are chosen in such a manner that Eqs. (41)-(44) converge at p = 1,
The general expressions of the solutions can be expressed as follows:
where f∗m (η),g∗m (η),θ∗m (η),and φ∗m(η) are the special functions.
4 Convergence analysis
The series solutions (45)-(48) involve the auxiliary parameters  f ,
f , g,
g, θ,and
θ,and  φ. These parameters are useful in adjusting and controlling the convergence of the obtained series solutions.
The proper values of these parameters are quite essential to construct the convergent solutions
through the HAM. To choose the suitable values of
φ. These parameters are useful in adjusting and controlling the convergence of the obtained series solutions.
The proper values of these parameters are quite essential to construct the convergent solutions
through the HAM. To choose the suitable values of  f ,
f , g,
g, θ,and
θ,and  φ,the
φ,the  -curves are drawn
at the 15th-order of approximations. Figures 2 and 3 clearly show that the convergence region
lies within the domain
-curves are drawn
at the 15th-order of approximations. Figures 2 and 3 clearly show that the convergence region
lies within the domain


 |
Fig. 2.  -curves for f"(0) and g'(0) when β = S = NT = 0.1,c = 0.2,
NB = 0.5,P r = 0.7,and Le = 1.0 -curves for f"(0) and g'(0) when β = S = NT = 0.1,c = 0.2,
NB = 0.5,P r = 0.7,and Le = 1.0 |
 |
Fig. 3.  -curves for θ'(0) and φ'(0) when β = S = NT = 0.1,c = 0.2,NB = 0.5,
P r = 0.7,and Le = 1.0 -curves for θ'(0) and φ'(0) when β = S = NT = 0.1,c = 0.2,NB = 0.5,
P r = 0.7,and Le = 1.0 |
Table 1 shows that the 32nd-order of approximations is sufficient for the convergent series solutions.
 f =
f =  g =
g =  θ =
θ =  φ = −1.2
φ = −1.2 |
The present section addresses the effects of various influential parameters,including the Deborah number β,the ratio parameter c,the Prandtl number Pr,the thermophoresis parameter NT,the Brownian motion parameter NB,the heat source/sink parameter S,and the Lewis number Le,on the dimensionless velocities,temperature,and nanoparticle concentration distributions. The results are shown in Figs. 4-18.
Figure 4 depicts the effects of the Deborah number β on the velocity field f'(η). From this figure,we can see that the velocity field f'(η) decreases when the Deborah number increases. Physically,the Deborah number depends on the relaxation time. It is well-known that larger relaxation time resists the fluid flow. Here,larger Deborah numbers correspond to larger relaxation time. Due to this reason,the velocity field f'(η) and the momentum boundary layer thickness decrease when the Deborah number increases. From Fig. 4,we can also see that the results with β = 0 correspond to the viscous fluid results. Figure 5 shows the effects of the ratio parameter c on the velocity field f'(η). The results show that the velocity and the related boundary layer thickness decrease when the ratio parameter increases. This is due to the reason that the x-component of the velocity reduces when the ratio parameter increases, which shows decreases in the velocity f'(η) and the momentum boundary layer thickness.
 |
| Fig. 4. Effects of β on f'(η) when S = NT = 0.1,c = 0.2,NB = 0.5,P r = 0.7,and Le = 1.0 |
 |
| Fig. 5. Effects of c on f'(η) when β = S = NT = 0.1,NB = 0.5,P r = 0.7,and Le = 1.0 |
Figure 6 shows the effects of the Deborah number β on the velocity field g'(η). The results show that the velocity and the associated boundary layer thickness decrease when the Deborah number β increases. Figure 7 describes the effects of the ratio parameter c on the velocity field g'(η). From this figure,we can see that the velocity and the related boundary layer thickness increase when the ratio parameter c increases. Combined the results shown in Figs. 5 and 7,we can see that f'(η) decreases while g'(η) increases when the ratio parameter increases. When c increases from zero,the lateral surface begins to move in the y-direction,and hence the velocity field g'(η) increases and the velocity field f'(η) decreases.
 |
| Fig. 6. Effects of β on g'(η) when S = NT = 0.1,c = 0.2,NB = 0.5,P r = 0.7,and Le = 1.0 |
 |
| Fig. 7. Effects of c on g'(η) when β = S = NT = 0.1,NB = 0.5,P r = 0.7,and Le = 1.0 |
Figures 8-12 show the effects of the Deborah number β,the ratio parameter c,the Prandtl number Pr,the thermophoresis parameter NT,and the heat source/sink parameter S on the temperature field θ(η),respectively.
 |
| Fig. 8. Effects of β on θ(η) when S = NT = 0.1,c = 0.2,NB = 0.5,P r = 0.7,and Le = 1.0 |
 |
| Fig. 9. Effects of c on θ(η) when β = S = NT = 0.1,NB = 0.5,P r = 0.7,and Le = 1.0 |
 |
| Fig. 10. Effects of P r on θ(η) when β = S = NT = 0.1,c = 0.2,NB = 0.5,and Le = 1.0 |
 |
| Fig. 11. Effects of NT on θ(η) when β = S = 0.1,c = 0.2,NB = 0.5,P r = 0.7,and Le = 1.0 |
 |
| Fig. 12. Effects of S on θ(η) when β = NT = 0.1,c = 0.2,NB = 0.5,P r = 0.7,and Le = 1.0 |
From Fig. 8,we can see that the temperature and the related thermal boundary layer thickness increase when the Deborah number increases. The Deborah number is directly proportional to the relaxation time,and the relaxation time is larger for higher Deborah numbers. Therefore, larger relaxation time corresponds to higher temperature and thicker related thermal boundary layer thickness. From Fig. 9,we can see that an increase in the ratio parameter leads to a reduction in the temperature field θ(η). For c = 0,the two-dimensional flow case is recovered. Here,we notice that the thermal boundary layer thickness is thicker for the two-dimensional flow case in comparison with the three-dimensional situation.
Figure 10 depicts that the temperature field θ(η) is higher for smaller Prandtl number P r. Physically,larger Prandtl number fluid possesses lower thermal diffusivity,and smaller Prandtl number fluid has higher thermal diffusivity. This change in the thermal diffusivity creates a reduction in the temperature θ(η) and the associated thermal boundary layer thickness. From Fig. 11,we can see that the temperature and the related thermal boundary layer thickness enhance when the thermophoresis parameter increases. Physically,the presence of nanoparticles increases the thermal conductivity of the fluid. It is well-known that whether the fluids with higher thermal conductivity have larger temperature is still debatable. Here,the temperature and the thermal boundary layer thickness increase due to such an argument. In Fig. 12,S > 0 is for heat source,and S < 0 is for heat sink. From Fig. 12,we can see that the temperature and the related thermal boundary layer thickness enhance in the case of heat source when we compare the results with those in the case of heat sink. For S > 0,more heat is produced by the fluid due to which the temperature and its related thermal boundary layer thickness increase.
The effects of the Deborah number β on the concentration field φ(η) are shown in Fig. 13. Here,the concentration φ(η) and the related boundary layer thickness are larger for higher β. Figure 14 shows the effects of ratio parameter c on the concentration field φ(η). It is shown that an increase in the ratio parameter c creates a reduction in the concentration φ(η) and a reduction in the the associated boundary layer thickness.
 |
| Fig. 13. Effects of β on φ(η) when S = NT = 0.1,c = 0.2,NB = 0.5,P r = 0.7,and Le = 1.0 |
 |
| Fig. 14. Effects of c on φ(η) when β = S = NT = 0.1,NB = 0.5,P r = 0.7,and Le = 1.0 |
Figure 15 shows the effects of Lewis number Le on the concentration field φ(η). From Fig. 15,we can see that the concentration field decreases when the Lewis number increases. The Lewis number is inversely proportional to the Brownian diffusion coefficient,and the Brownian diffusion coefficient is weaker for higher Le. This weaker Brownian diffusion coefficient creates a reduction in the concentration field. Figure 16 shows the effects of the Prandtl number P r on the concentration distribution φ(η). It is noted that both the concentration φ(η) and the associated boundary layer thickness decrease when the Prandtl number P r increases.
 |
| Fig. 15. Effects of Le on φ(η) when β = S = NT = 0.1,c = 0.2,NB = 0.5,and P r = 0.7 |
 |
| Fig. 16. Effects of P r on φ(η) when β = S = NT = 0.1,c = 0.2,NB = 0.5,and Le = 1.0 |
Figure 17 shows the effects of the thermophoresis parameter NT on the concentration φ(η). It is shown that the concentration φ(η) and its related boundary layer thickness increase when NT increases. Moreover,when the thermophoresis parameter increases,the thermal conductivity of the fluid increases due to the stronger concentration and the stronger related boundary layer thickness. Figure 18 shows the effects of the Brownian motion parameter NB on the concentration field φ(η). The results show that the concentration φ(η) and the associated concentration boundary layer thickness decrease when NB increases.
 |
| Fig. 17. Effects of NT on φ(η) when β = S = 0.1,c = 0.2,NB = 0.5,P r = 0.7,and Le = 1.0 |
 |
| Fig. 18. Effects of NB on φ(η) when β = S = NT = 0.1,c = 0.2,P r = 0.7,and Le = 1.0 |
Table 2 presents the numerical values of the local Nusselt number for various values of β,c, P r,S,NT,NB,and Le. The results show that the local Nusselt number decreases when β,S, NT,or Le increases,while increases when c or P r increases.
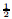 Nux for different values of β,c,Pr,S,
NT,NB,and Le
Nux for different values of β,c,Pr,S,
NT,NB,and Le |
The three-dimensional boundary layer flow of Maxwell nanofluid with heat source/sink is investigated. The main points of the present analysis are listed as follows:
(i) f'(η) and g'(η) decrease while θ(η) and φ(η) increase when β increases.
(ii) The effects of c on f'(η) and g'(η) are quite opposite,while the effects of c on θ(η) and φ(η) are similar.
(iii) When P r increases,θ(η) and the associated thermal boundary layer thickness decrease.
(iv) The temperature profile increases when NT and S increase.
(v) When the Lewis number and the Prandtl number increase,φ(η) decreases.
(vi) φ(η) decreases when NB increases,while increases when NT increases.
| [1] | Masuda, H., Ebata, A., Teramae, K., and Hishiunma, N. Alteration of thermal conductivity and viscosity of liquid by dispersed ultra-fine particles (dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles). Netsu Bussei, 4, 227-233 (1993) |
| [2] | Choi, S. U. S. and Eastman, J. A. Enhancing thermal conductivity of fluids with nanoparticles. ASME International Mechanical Engineering Congress & Exposisition, American Society of Mechanical Engineers, San Francisco (1995) |
| [3] | Buongiorno, J. Convective transport in nanofluids. Journal of Heat Transfer, 128, 240-250 (2006) |
| [4] | Khan, W. A. and Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. International Journal of Heat and Mass Transfer, 53, 2477-2483 (2010) |
| [5] | Turkyilmazoglu, M. Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids. Chemical Engineering Science, 84, 182-187 (2012) |
| [6] | Makinde, O. D., Khan, W. A., and Khan, Z. H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. International Journal of Heat and Mass Transfer, 62, 526-533 (2013) |
| [7] | Rashidi, M. M., Abelman, S., and Mehr, N. F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. International Journal of Heat and Mass Transfer, 62, 515-525 (2013) |
| [8] | Sheikholeslami, M. and Ganji, D. D. Heat transfer of Cu-water nanofluid flow between parallel plates. Powder Technology, 235, 873-879 (2013) |
| [9] | Mustafa, M., Farooq, M. A., Hayat, T., and Alsaedi, A. Numerical and series solutions for stagnation point flow of nanofluid over an exponentially stretching sheet. PloS One, 8, e61859 (2013) |
| [10] | Kuznetsov, A. V. and Nield, D. A. Natural convective boundary-layer flow of a nanofluid past a vertical plate: a revised model. International Journal of Thermal Sciences, 77, 126-129 (2014) |
| [11] | Wang, S. and Tan, W. Stability analysis of Soret-driven double-diffusive convection of Maxwell fluid in a porous medium. International Journal of Heat and Fluid Flow, 32, 88-94 (2011) |
| [12] | Fetecau, C., Fetecau, C., Jamil, M., and Mahmood, A. Flow of fractional Maxwell fluid between coaxial cylinders. Archive of Applied Mechanics, 81, 1153-1163 (2011) |
| [13] | Hayat, T., Shehzad, S. A., Qasim, M., and Obaidat, S. Steady flow ofMaxwell fluid with convective boundary conditions. Zeitschrift für Naturforschung A, 66a, 417-422 (2011) |
| [14] | Mukhopadhyay, S. Heat transfer analysis of the unsteady flow of a Maxwell fluid over a stretching surface in the presence of a heat source/sink. Chinese Physics Letters, 29, 054703 (2012) |
| [15] | Abel, M. S., Tawade, V., and Shinde, N. The effects of MHD flow and heat transfer for the UCM fluid over a stretching surface in presence of thermal radiation. Advances in Mathematical Physics, 21, 702681 (2012) |
| [16] | Hayat, T., Shehzad, S. A., Al-Sulami, H. H., and Asghar, S. Influence of thermal stratification on the radiative flow of Maxwell fluid. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 35, 381-389 (2013) |
| [17] | Abbasbandy, S., Hayat, T., Ghehsareh, H. R., and Alsaedi, A. MHD Falkner-Skan flow of Maxwell fluid by rational Chebyshev collocation method. Applied Mathematics and Mechanics (English Edition), 34, 921-930 (2013) DOI 10.1007/s10483-013-1717-7 |
| [18] | Shehzad, S. A., Alsaedi, A., and Hayat, T. Hydromagnetic steady flow of Maxwell fluid over a bidirectional stretching surface with prescribed surface temperature and prescribed surface heat flux. PloS One, 8, e68139 (2013) |
| [19] | Liao, S. J. Homotopy Analysis Method in Nonlinear Differential Equations, Springer, Heidelberg (2012) |
| [20] | Turkyilmazoglu, M. Solution of the Thomas-Fermi equation with a convergent approach. Communications in Nonlinear Science and Numerical Simulation, 17, 4097-4103 (2012) |
| [21] | Rashidi, M. M., Keimanesh, M., and Rajvanshi, S. C. Study of pulsatile flow in a porous annulus with the homotopy analysis method. International Journal of Numerical Methods for Heat & Fluid Flow, 22, 971-989 (2012) |
| [22] | Shehzad, S. A., Alsaedi, A., Hayat, T., and Alhuthali, M. S. Three-dimensional flow of an Oldroyd-B fluid with variable thermal conductivity and heat generation/absorption. PloS One, 8, e78240 (2013) |
| [23] | Abbasbandy, S., Hashemi, M. S., and Hashim, I. On convergence of homotopy analysis method and its application to fractional integro-differential equations. Quaestiones Mathematicae, 36, 93-105 (2013) |
| [24] | Hayat, T., Shehzad, S. A., Alsaedi, A., and Alhothuali, M. S. Three-dimensional flow of Oldroyd-B fluid over surface with convective boundary conditions. Applied Mathematics and Mechanics (English Edition), 34, 489-500 (2013) DOI 10.1007/s10483-013-1685-9 |
| [25] | Hayat, T., Shehzad, S. A., and Alsaedi, A. Three-dimensional stretched flow of Jeffrey fluid with variable thermal conductivity and thermal radiation. Applied Mathematics and Mechanics (English Edition), 34, 823-832 (2013) DOI 10.1007/s10483-013-1710-7 |
| [26] | Imtiaz, M., Hayat, T., Hussain, M., Shehzad, S. A., Chen, G. Q., and Ahmad, B. Mixed convection flow of nanofluid with Newtonian heating. The European Physical Journal Plus, 129, 97 (2014) |
| [27] | Hayat, T. and Awais, M. Three-dimensional flow of upper-convected Maxwell (UCM) fluid. International Journal for Numerical Methods in Fluids, 66, 875-884 (2011) |
| [28] | Harris, J. Rheology and Non-Newtonian Flow, Longman, London (1977) |
| [29] | Schilchting, H. Boundary Layer Theory, McGraw-Hill, New York (1964) |
 2015, Vol. 36
2015, Vol. 36























