Shanghai University
Article Information
- Zhijun LIU, Tangdai XIA, Qingqing ZHENG, Weiyun CHEN. 2015.
- Comparison about parametric effects on wave propagation characteristics
- Appl. Math. Mech. -Engl. Ed., 36(6): 763-776
- http://dx.doi.org/10.1007/s10483-015-1944-6
Article History
- Received 2014-5-26;
- in final form 2014-12-8
2. Institute of Geotechnical Engineering, Nanjing Tech University, Nanjing 210009, China
As we know,every kind of waves contains the information about the physical properties of the propagation medium. Therefore,the analysis of wave propagation is not only of great significance in theoretical study but also of distinctive practical value in many engineering fields such as geotechnical engineering,oil exploration,earthquake engineering,and vibration test[1, 2]. To achieve that,it is essential to study the relation between the parameters about the physical properties of the medium and the waves propagating in it. Porous media,such as saturated and unsaturated media,are very common in reality. In the past years,the effects of the parameters on the waves in porous media have been widely studied.
(i) The waves propagating in porous media have been widely studied in the cases of considering or neglecting the compressibility of the solid grain[3, 4, 5, 6, 7]. However,those studies were conducted separately,and no comparison has ever been made between the results in those two different cases. Consequently,we have no idea about the effects on the results in the case of neglecting the compressibility of solid grain. Therefore,it is necessary to make assessment about the effects of the compressibility of solid grain.
(ii) The frequency effects have been widely investigated on the wave propagation velocity and attenuation[8, 9, 10, 11, 12]. Beskos et al.[13] conducted a numerical analysis about the frequency effects on the velocities and attenuations of bulk waves in saturated rocks with different combinations of porosities and permeabilities. Kim et al.[14] and Sharma[15] numerically illuminated how the velocities and attenuations of the bulk waves in dissipative porous media were affected by a combined parameter,namely,the product of frequency and fluid viscosity. Thereinto,Kim et al.[14] compared the results in the cases with different values of porosity,bulk modulus of solid skeleton,and Poisson’s ratio. Lu et al.[11] showed the frequency effects on the propagation characteristics of the bulk waves under several different values of fluid viscosity. Liu and De Boer[8],Zhang et al.[16],and Chen et al.[17] numerically analyzed the effects of frequency and saturation on the velocities and attenuations of the surface waves in the cases of several different values of permeability,Poisson’s ratio,and coupling-damping coefficient (a combined parameter of porosity,fluid viscosity,and permeability). To sum up,apart from frequency,the analysis about how the wave propagation velocity and attenuation vary with the continuous change of each single parameter has seldom been made.
(iii) Among the available references,only Yang et al.[18] once numerically analyzed the variations of the propagation velocities and attenuations of the bulk waves in saturated soils with continuous changes in the frequency,porosity,permeability,and fluid viscosity,respectively. However,in the numerical calculation,the relation between the porosity and the moduli of the porous media (porosity-moduli relation for short) was not considered. Instead,when the porosity effects on the wave propagationcharacteristics were analyzed,the bulk modulus and the shear modulus of the solid skeleton were assumed to be constants when the porosity increased. For instance,the bulk modulus and the shear modulus of the solid skeleton in the case of n = 0.05 (n,the notation of porosity) were the same as those in the case of n = 0.9. Obviously,that kind of processing is unreasonable,and does not agree with the fact. Besides,the degeneration of the numerical results and the effect of Poisson’s ratio were not discussed.
Based on the deficiencies mentioned above,the present paper further analyzes the effects of frequency on the propagation characteristics of the bulk waves in a saturated porous medium. The numerical results in the cases of considering and neglecting the compressibility of the solid grain are compared. Then,the obtained results are compared with those of Yang et al.[18]. The effects of the porosity and Poisson’s ratio on the wave propagation velocity and attenuation are studied with the consideration of the porosity-moduli relation,and the degeneration of the numerical results is also discussed. Conclusions are given in the end.
2 Basic theoretical framework2.1 Governing equations
In Biot’s theory[19],the dynamic governing equations for wave propagation in saturated porous media can be expressed in terms of the displacements as follows:
where e = ∇u,and ε = ∇U,in which u and U are the displacement vectors for the solid phase and the fluid phase,respectively. b = n2η/κd,where n is the porosity of the porous medium. η is the fluid viscosity,and κd is the intrinsic permeability (with the dimension L2). ρ11 and ρ22 represent the mass coefficients of the solid phase and the fluid phase,respectively. ρ12 represents the mass coupling coefficient between the solid phase and the fluid phase. nρf = ρ12 + ρ22,and (1 − n)ρs = ρ11+ρ12,where ρs and ρf represent the density of solid grain and fluid,respectively. A,R,Q,and N are the Biot elastic coefficients,and they can be expressed as follows: where λ and μ are the Lame constants of the solid skeleton,respectively. α and M are the Biot coefficients representing the compressibility of the fluid and solid grain,respectively.The expressions of A,R,and Q are usually different in the literature[20, 21, 22]. However, they are essentially consistent after substituting the relations among the parameters mentioned below.
When the compressibility of the solid grain is considered,the relation between the two Biot coefficients,α and M,and the bulk moduli of the porous media can be expressed as follows:
where Ks,Kb,and Kf are the bulk moduli of the solid grain,the solid skeleton,and the fluid,respectively.When the compressibility of solid grain is neglected,i.e.,Ks → ∞,Eq. (3) can be rewritten as follows:
As we know,for the elastic solid skeleton,the stress-strain relation is
From Eq. (5),we can derive and εv is the volumetric strain expressed defined by
According to the elastic theory,we have
where E and ν are the elastic modulus and Poisson’s ratio of the solid skeleton,respectively.Combining Eqs. (6)-(8),we have
For a porous medium whose constituents are ascertained,the bulk moduli of the solid grain and fluid,i.e.,Ks and Kf,are constants,while the bulk modulus of the solid skeleton,Kb,will decrease with the increase in the porosity. Ignoring the porosity effect on the relevant Poisson ratio,Luo and Stevens[23] described the relation between Kb and the porosity as follows: As we can see from Eqs. (9)-(12),for a porous medium whose constituents are ascertained,the bulk modulus of the solid grain,Ks,is invariable. However,the bulk modulus and the Lame constants of the solid skeleton,i.e.,Kb,λ,and N,will vary when the porosity and Poisson ratio change. 2.2 Theoretical solutionAccording to the Helmholtz decomposition theorem,the displacement vectors u and U can be decomposed into
where φs and φf are the scalar potentials of the solid displacement and fluid displacement, respectively. ψs and ψf are the vector potentials satisfying
Substituting the divergence and the curl operator into Eq. (1),respectively,we can obtain the governing equations for the compressional wave and the shear wave propagating in the saturated porous media as follows[24]:
where
The general form of the solution for the plane bulk waves can be assumed as follows:
where i is the imaginary unit,i=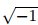 . ω is the angular frequency defined by
. ω is the angular frequency defined by

In this paper,we only study the bulk waves in a two-dimensional plane,i.e.,the xz-plane of the Cartesian coordinate system. Therefore,

Substituting Eq. (16) into Eq. (14),we can obtain
where vp is the theoretical expression for the velocity of the compressional wave defined by

To guarantee the existence of nonzero solutions for As and Af in Eq. (18),the following condition must be satisfied:
Simplifying Eq. (19),we obtain From Eq. (20),we can draw the conclusion that there exist two kinds of compressional waves in a saturated porous medium,which are known as the fast compressional wave,P1,and the slow compressional wave,P2. Furthermore,we assume that the theoretical solutions of Eq. (20) are vp1 and vp2. Therefore,the corresponding complex wave numbers are where vp1 and vp2 are the theoretical expressions for the wave velocities of the P1 wave and the P2 wave,respectively,and both of them are complex numbers. Here,for the purpose of discussion,we define vp1 and vp2 as complex velocities.Take the absolute value of the imaginary part of kpi as the attenuation coefficient. Then, the attenuations of the P1 wave and the P2 wave can be defined by
where Im represents the imaginary part of a complex number.When the propagation characteristics of the waves in porous media are studied,some researchers[8, 25, 26] take the real part of the complex velocity,i.e.,Re(vpi),as the wave propagation velocity. However,it is more reasonable and more widely accepted to take the phase velocity as the wave propagation velocity[10, 15, 16, 27],i.e.,
Substituting Eq. (17) into Eq. (15),we can obtain
To guarantee the existence of nonzero solutions for Bs and Bf in Eq. (24),the following condition must be satisfied: Simplifying Eq. (25),we obtain From Eq. (26),we can infer that there exists one shear wave,i.e.,the S wave,in a saturated porous medium,and obtain the complex velocity vs. The complex wave number for the S wave is Similarly,the attenuation of the S wave,δs,is defined by and the wave propagation velocity is 3 Numerical results and discussionSince the numerical results about the effects of permeability and fluid viscosity on the bulk waves in the case of considering the porosity-moduli relation are consistent with those obtained by Yang et al.[18] in which the porosity-moduli relation is neglected,we focus on analyzing the effects of frequency,porosity,and Poisson’s ratio in the following.
The common parameters for the numerical calculation are as follows:

Figure 1 depicts the effects of frequency on the propagation velocities and attenuations of the bulk waves in a saturated porous medium in the cases of considering and neglecting the compressibility of solid grain,respectively.
As we can see from Fig. 1,for each bulk wave,the variation tendency of the velocity is consistent with that of the attenuation. The P1 wave,known as the fast compressional wave, propagates the fastest,while attenuates the most slowly. The P2 wave,known as the slow compressional wave,attenuates the fastest.
Biot[19] introduced a characteristic frequency as follows:
Substituting the values of the relevant parameters into Eq. (30),the characteristic frequency of the porous medium considered here is fc = 2 547 Hz.According to the numerical results and the position of fc shown in Fig. 1,the whole frequency band can be divided into three parts,i.e.,low frequency band,medium frequency band,and high frequency band. Specifically,,the medium frequency band refers to a certain frequency range around fc,and the left and right sides of the medium frequency band are the low frequency band and the high frequency band,respectively.
Based on the above analysis,more details regarding the frequency effects are found as follows.
(i) For the P1 wave and the S wave,both the velocities and attenuations almost keep constant in the low frequency band and the high frequency band,while grow rapidly with the increase in the frequency in the medium frequency band. It is also worth pointing out that the attenuations of the P1 wave and the S wave are nearly zero in the low frequency band.
(ii) For the P2 wave,unlike the P1 wave and the S wave whose variation curves can be distinctly divided into three different segments,when the frequency increases,the velocity and attenuation grow at first,and then almost keep invariable when the frequency is beyond fc.
From Fig. 1,we can also compare the results in the cases of considering and neglecting the compressibility of solid grain.
In the case of considering the compressibility of solid grain,substituting the values of the relevant parameters into Eq. (3),we can obtain the Biot coefficient α,i.e.,α = 1/3. According to Eq. (4),the case when α = 1 corresponds to the case of neglecting the compressibility of solid grain.
Figure 1 also shows that whether considering the compressibility of solid grain or not,there is no effect on the variation tendency of the curves.
For the P1 wave,the velocity in the case when α = 1 is greater than that in the case when α = 1/3,and the two curves are almost parallel to each other (see Fig. 1(a)). Instead, the attenuation in the case when α = 1/3 is greater than that in the case when α = 1. The discrepancy between them is quite tiny in the low frequency band,and then gradually enlarges in the medium frequency band. When the frequency increases to the high frequency band,the discrepancy keeps constant.
 |
| Fig. 1. Variation curves of propagation velocities and attenuations of bulk waves versus frequency when ν = 0.2 and n = 0.2 |
For the P2 wave,the velocity corresponding to α = 1/3 is slightly greater than that corresponding to α = 1,while the attenuation is the opposite. Besides,within the characteristic frequency,the difference between the two velocity curves is tiny,which is also the case for the attenuation curves.
For the S wave,the curves when α = 1/3 and α = 1 almost overlap each other,which means that the compressibility of solid grain has little effect on the velocity and attenuation of the S wave.
3.2 Effect of porosityAs mentioned before,compared with Yang et al.[18],this paper considers the porosity-moduli relation of the porous media. Based on the methods used by this paper and Yang et al.[18],the porosity effects on the propagation velocities and attenuations of bulk waves are illustrated in Fig. 2,and the range of the porosity discussed here is from 0.001 to 0.999.
 |
| Fig. 2. Variation curves of propagation velocities and attenuations of bulk waves versus porosity when ν = 0.2 and f = 100 Hz |
As shown in Fig. 2,there exist obvious changes in the velocities and attenuations as the porosity varies,and the numerical results obtained by the methods of this paper and Yang et al.[18] are remarkably different.
For the P1 wave,based on the theory of this paper,as the porosity increases from 0.001 to 0.999,the velocity decreases,while the attenuation increases gently at first,and then decreases. Instead,in the case of Yang et al.[18],the velocity grows with the increase in the porosity,while the attenuation grows sharply at the beginning,and then decreases.
For the P2 wave,the velocities of both the two cases almost vary in the same route,decreasing with the increase in the porosity. However,the starting points and the ending points of the two curves are different. So far as attenuation is concerned,in the case of this paper,it grows slightly at first,and then increases sharply when the porosity approaches 1.0. However,in the case of Yang et al.[18],the attenuation grows sharply at the very beginning,and then almost keeps invariable.
For the S wave,both the velocities and the attenuations corresponding to the cases of this paper and Yang et al.[18] vary in the opposite way. Specifically,in the case of this paper,the velocity decreases with the increase in the porosity,and the attenuation grows gently at first, and then increase sharply when the porosity gets close to 1.0.
In the above analysis,we have compared the numerical results of this paper and Yang et al.[18]. In the following,through a degeneration analysis,we will further discuss the rationality of the results obtained by the two cases.
When n = 0,the saturated porous medium degenerates into an elastic solid,where only two kinds of bulk waves exist,i.e.,the compressional wave and the shear wave,and the slowcompressional wave,P2,disappears. As we know,the bulk waves in an elastic solid are of no attenuation. Just as shown in Figs. 2(b),2(d),and 2(f),the attenuations of both this paper and Yang et al.[18] are nearly zero when n is 0.001.
In the case when n = 0,according to Eqs. (7)-(12),the relevant parameters of the elastic solid are
Then,the velocities of the compressional wave and the shear wave in the elastic solid areIn the above numerical calculation,when n = 0.001,the results of this paper are


When n = 1,the saturated porous medium degenerates into a pure fluid. The fluid is assumed to be unable to sustain the shear strain in Biot’s theory. Therefore,only a kind of bulk wave,namely,the compressional wave,exists in the fluid,and the P2 wave and the S wave disappear. Consequently,when the porosity approaches 1.0,the attenuation of the P1 wave is supposed to decrease to nearly zero,while the attenuations of the P2 wave and the S wave are supposed to grow rapidly. As shown in Figs. 2(b),2(d),and 2(f),when n gets close to 1.0,the attenuations of the P1 wave in the cases of both this paper and Yang et al.[18] decrease close to zero,and the attenuations of the P2 wave and the S wave in the case of this paper exhibit a rapid increase. However,the attenuations of the P2 wave and the S wave in the case of Yang et al.[18] have no obvious changes when n approaches 1.0,and are much smaller than the results of this paper.
In the case of n = 1,combined with Eqs. (7)-(12),the corresponding parameters of the fluid are
Then,the velocity of the compressional wave in the fluid isAccording to the numerical calculation,when n = 0.999,the velocity of the P1 wave of this paper is


As we can infer from the above degeneration analysis,although both this paper and Yang et al.[18] are based on Biot’s theory,this paper considers the porosity-moduli relation of the porous media in the parametric studies. Therefore,the numerical results of this paper are more rational than those of Yang et al.[18].
3.3 Effects of Poisson’s ratioFigure 3 shows the effects of Poisson’s ratio ν on the propagation velocities and attenuations of the bulk waves. The values of ν considered here are from 0.01 to 0.498.
From Figs. 3(a),3(c),and 3(e),we can see that the velocities of the P1 wave and the S wave almost decrease linearly when ν increases. While for the P2 wave,the velocity decreases quite slightly at the beginning,and then decreases sharply when ν gets close to 0.5. Instead,as shown in Figs. 3(b),3(b),and 3(f),the attenuations of the P2 wave and the S wave grow gently with the increase in ν at first,and then increase sharply when ν approaches 0.5. For the P1 wave, the attenuation increases at first,then decreases,and has a rapid increase when ν approaches 0.5. Besides,the numerical results shown in Fig. 3 also verify the former conclusion that the P2 wave attenuates the fastest. The attenuation of the P2 wave has orders of magnitude larger than those of the P1 wave and the S wave.
 |
| Fig. 3. Variation curves of propagation velocities and attenuations of bulk waves versus Poisson’s ratio when n = 0.2 and f = 100 Hz |
In this paper,considering the porosity-moduli relation of the porous medium,we study the effects of frequency,porosity,and Poisson’s ratio on the propagation characteristics of bulk waves in saturated porous media,and compare the obtained results with those of Yang et al.[18]. Conclusions can be drawn as follows.
(i) According to the characteristic frequency,fc,the whole frequency band can be naturally divided into three parts,i.e.,,low frequency band,medium frequency band,and high frequency band. For the P1 wave and the S wave,both the velocities and attenuations almost keep invariable in the low frequency band and the high frequency band,while grow sharply in the medium frequency band. For the P2 wave,the velocity and attenuation grow with the increase in the frequency within fc,and then keep constant when the frequency is beyond fc.
(ii) The compressibility of the solid grain has a distinctive effect on the P1 wave,and a tiny effect on the P2 wave,while no effect on the S wave.
(iii) For a saturated porous medium whose constituents are ascertained,in the case of considering the porosity-moduli relation,the velocity of each bulk wave decreases as n increases from 0.001 to 0.999,and the attenuation of the P1 wave increases gradually firstly,then decreases to nearly zero,while the attenuations of the P2 wave and the S wave grow slightly at first,then increase sharply when n gets close to 1.0.
(iv) In contrast with the case of neglecting the porosity-moduli relation,the numerical results in the case of considering the porosity-moduli relation can be degenerated into the results of elastic solid and pure fluid,thereby verifying the rationality of this paper. The porosity-moduli relation cannot be neglected when the porosity effects on the wave propagation characteristics are studied.
(v) Poisson’s ratio ν has obvious effects on the propagation characteristics of the bulk waves in saturated porous media. Generally speaking,as ν increases,the velocities of the P1 wave, the P2 wave,and the S wave decrease all the way,while the attenuations vary gently at the beginning,and then grow rapidly when ν approaches 0.5.
| [1] | Yi, T. H., Li, H. N., and Gu, M. Effect of different construction materials on propagation of GPS monitoring signals. Measurement, 45, 1126-1139 (2012) |
| [2] | Yi, T. H., Li, H. N., and Zhao, X. Y. Noise smoothing for structural vibration test signals using an improved wavelet thresholding technique. Sensors, 12, 11205-11220 (2012) |
| [3] | De Boer, R. and Liu, Z. F. Propagation of acceleration waves in incompressible saturated porous solids. Transport in Porous Media, 21, 163-173 (1995) |
| [4] | Yang, J. A note on Rayleigh wave velocity in saturated soils with compressible constituents. Canadian Geotechnical Journal, 38, 1360-1365 (2001) |
| [5] | Kumar, R. and Hundal, B. S. Symmetric wave propagation in a fluid-saturated incompressible porous medium. Journal of Sound and Vibration, 288, 363-373 (2005) |
| [6] | Kumar, R. and Hundal, B. S. Surface wave propagation in a fluid-saturated incompressible porous medium. Sadhana, 32, 155-166 (2007) |
| [7] | Zhou, F. X., Lai, Y. M., and Song, R. X. Propagation of plane wave in non-homogeneously saturated soils. Science China Technological Sciences, 56, 430-440 (2013) |
| [8] | Liu, Z. F. and de Boer, R. Dispersion and attenuation of surface waves in a fluid-saturated porous medium. Transport in Porous Media, 29, 207-223 (1997) |
| [9] | Berryman, J. G. and Wang, H. F. Elastic wave propagation and attenuation in a double porosity dual-permeability medium. International Journal of Rock Mechanics and Mining Sciences, 37, 63-78 (2000) |
| [10] | Dai, Z. J., Kuang, Z. B., and Zhao, S. X. Rayleigh waves in a double porosity half-space. Journal of Sound and Vibration, 298, 319-332 (2006) |
| [11] | Lu, J. F., Hanyga, A., and Jeng, D. S. A linear dynamic model for a saturated porous medium. Transport in Porous Media, 68, 321-340 (2007) |
| [12] | Nenadic, I. Z., Urban, M. W., Bernal, M., and Greenleaf, J. F. Phase velocities and attenuations of shear, Lamb, and Rayleigh waves in plate-like tissues submerged in a fluid (L). Journal of the Acoustical Society of America, 130, 3549-3552 (2011) |
| [13] | Beskos, D. E., Vgenopoulou, I., and Providakis, C. P. Dynamics of saturated rocks, II: body waves. Journal of Engineering Mechanics, 115, 996-1016 (1989) |
| [14] | Kim, S. H., Kim, K. J., and Blouin, S. E. Analysis of wave propagation in saturated porous media, II: parametric studies. Computer Methods in Applied Mechanics and Engineering, 191, 4075-4091 (2002) |
| [15] | Sharma, M. D. Wave propagation in a dissipative poroelastic medium. IMA Journal of Applied Mathematics, 78, 59-69 (2013) |
| [16] | Zhang, Y., Xu, Y. X., and Xia, J. H. Analysis of dispersion and attenuation of surface waves in poroelastic media in the exploration-seismic frequency band. Geophysical Journal International, 187, 871-888 (2011) |
| [17] | Chen, W. Y., Xia, T. D., and Hu,W. T. A mixture theory analysis for the surface wave propagation in an unsaturated porous medium. International Journal of Solids and Structures, 48, 2402-2412 (2011) |
| [18] | Yang, J., Wu, S. M., and Cai, Y. Q. Characteristics of propagation of elastic waves in saturated soils (in Chinese). Journal of Vibration Engineering, 9, 128-137 (1996) |
| [19] | Biot, M. A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Journal of the Acoustical Society of America, 28, 168-191 (1956) |
| [20] | Depollier, C., Allard, J. F., and Lauriks, W. Biot theory and stress-strain equations in porous sound-absorbing materials. Journal of the Acoustical Society of America, 84, 2277-2279 (1988) |
| [21] | Smeulders, D. M. J., de la Rosette, J. P. M., and van Dongen, M. E. H. Waves in partially saturated porous media. Transport in Porous Media, 9, 25-37 (1992) |
| [22] | Lin, C. H., Lee, V. W., and Trifunac, M. D. The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid. Soil Dynamics and Earthquake Engineering, 25, 205-223 (2005) |
| [23] | Luo, J. and Stevens, R. Porosity-dependence of elastic moduli and hardness of 3Y-TZP ceramics. Ceramics International, 25, 281-286 (1999) |
| [24] | Tajuddin, M. Rayleigh waves in a poroelastic half-space. Journal of the Acoustical Society of America, 75, 682-684 (1984) |
| [25] | Yang, J. Rayleigh surface waves in an idealised partially saturated. Géotechnique, 55, 409-414 (2005) |
| [26] | Zhang, Y., Xu, Y. X., Xia, J. H., Zhang, S. X., and Ping, P. On effective characteristic of Rayleigh surface wave propagation. Soil Dynamics and Earthquake Engineering, 57, 94-103 (2014) |
| [27] | Singh, B. Reflection of plane waves from a free surface of a porothermoelastic solid half-space. Journal of Porous Media, 16, 945-957 (2013) |
 2015, Vol. 36
2015, Vol. 36































