1 Introduction

Due to the wide use of piezoelectric ceramics in smart structures,the study of the fracture of this type of materials becomes extremely important. Piezoelectric materials are composed of passive elastic materials and active piezoelectric materials. The high performance structures of piezoelectric materials have attracted wide attention in recent years^{[1, 2]}. The electromechanical properties of functionally graded piezoelectric (FGP) materials continuously vary in certain directions to compensate the sharp change in the electromechanical fields causing catastrophic failures. The promising properties of FGP materials make them suitable in many high-tech applications in electromechanical and electronic devices such as spacecraft,active noise and vibration suppression of aircraft wings,control of satellites,position control of flexible robot arms,smart skin systems for submarines,and shape control of advanced structures. However,it is generally well-known that piezoelectric ceramics are very brittle with low toughness. Therefore,the demand for lower failure rates during manufacturing and the promising applications of them require a better understanding of the fracture mechanism.

Although studying the effects of the crack propagation speed on the mechanical intensity factors of conventional materials is a well-known subject in the classical elastodynamics,with the increasing usage of piezoelectric materials and composites as actuating and sensing devices in smart structures,where the dynamic loading is dominant,much attention has been paid to the dynamic fracture behaviors. The mechanism of crack propagation and the effects of the crack propagation speed on the field intensity factors for FGP materials have not yet been discovered. Currently,the moving crack problems in piezoelectric materials under mechanical and electrical loads are attracting more and more attention of researchers. Yoffe^[3] considered the problem of a crack with fixed length at a constant speed through a body subjected to the uniform far field tensile loading for the first time. Chen and Yu^[4] first investigated the Yoffe crack problem in a piezoelectric material. The result implied that the moving speed of the crack had no influence on the intensities of the stress and electric displacement. Chen et al.^[5] studied the problem of a finite Griffith crack moving along the interface of two dissimilar piezoelectric half planes,and showed that the stress and electric displacement intensity factors depended on the crack speed under the impermeable condition at the crack surface. Kwon and Lee^[6] studied the dynamic crack propagation along the interface of a two-layered strip composed of a piezoelectric ceramic and an elastic layer. Li et al.^[7] investigated a moving interfacial crack between two bonded dissimilar piezoelectric materials. Gao et al.^[8] considered the problem of a moving interfacial crack between two dissimilar piezoelectric media,and discussed the effects of the crack speed on the fields’ singularities. Kwon and Lee^[9] investigated the propagating problem of a finite crack in a rectangular piezoelectric ceramic block under the combined anti-plane shear and in-plane electrical loadings. Li and Weng^[10] studied the dynamic behavior of a moving crack in an FGP material. They observed that the magnitudes of the stress and electric displacement intensity factors decreased when the gradient of the material properties increased. Lee et al.^[11] solved the dynamic problem of an interfacial crack moving along the interface between a piezoelectric and two orthotropic materials under electromechanical longitudinal shear loadings. Jin and Zhong^[12] investigated a moving crack in the FGP materials,and studied the effects of the crack propagation velocity and the gradient parameter of the FGP materials on the stress intensity factor. Li^[13] solved the dynamic problem of an impermeable crack of the length 2a propagating in a piezoelectric strip. Kwon^[14] studied the problem for the crack propagating at a constant speed in an FGP ceramic strip under combined anti-plane shear and in-plane electrical loadings. Ma et al.^[15] investigated a finite crack with constant length propagating in the functionally graded orthotropic strip under in-plane loading,and studied the effects of the material properties,the thickness of the functionally graded orthotropic strip,and the speed of the crack propagating upon the dynamic fracture behaviors. Yan and Jiang^[16] investigated the problem of a propagating finite crack in FGP materials. Lapusta et al.^[17] analyzed the plane problem for a crack moving with a subsonic speed along the interface of two piezoelectric semi-infinite spaces,and studied the effects of the crack speed on the stress intensity factors and energy release rate. Rokne et al.^[18] studied the dynamic behaviors of a moving Griffith crack under the anti-plane shear in a piezoelectric layer bounded by two elastic infinite spaces, and obtained the stress intensity factors and electric intensity displacement factors at the crack tips and energy release rate.

The solution procedures devised in all the above studies are neither capable of handling multiple cracks nor arbitrary arrangement. Using the dislocation solutions as a Green function provides the capability of the analysis of multiple cracks with arbitrary arrangement. In this technique,the dislocations are distributed along the crack configurations to model the fracture problem. Recently,this method has been successfully applied to the analysis of piezoelectric materials. Asadi^[19] determined the field intensity factors for a system of interacting annular and/or penny-shaped cracks. He defined the solution of annular electric dislocation,and solved it together with the annular climb and glide edge dislocations in an infinite transversely isotropic piezoelectric medium. Mousavi and Paavola^[20] used the distributed dislocation technique to the static analysis of cracked FGP layers,and studied the interaction of multiple cracks. Furthermore,Mousavi and Paavola^[21] extended this technique for a more general case to the static analysis of a magneto-electro-elastic layer with multiple cracks.

The objective of the present study is to provide closed form relations for the electromechanical fields at an FGP strip weakened by multiple moving cracks under anti-plane mechanical and in-plane electrical loadings. The elastic stiffness constants and mass density of materials are assumed to vary exponentially,perpendicular to the direction of the crack propagation. In this paper,a distributed dislocation technique is used to analyze the dynamic stress intensity factors of multiple moving cracks with arbitrary patterns located at the FGP strip. The complex Fourier transform is used to obtain the transformed displacement and stress fields. The dislocation solutions are then used to formulate the integral equations for an FGP layer weakened by several moving cracks. Numerical results are provided to show the effects of the crack propagation speed and the electromechanical material properties on the resulting field intensity factors.

2 Problem formulation

Consider an FGP strip,which is thick enough in the poling axis Z-direction so as to allow a state of anti-plane shear. The principal axes of the FGP material are taken to coincide with the reference axes X,Y ,and Z. The Volterra-type screw dislocation is used,where the cut itself lies parallel to the edges of the strip. It moves along the X-axis with the constant velocity V (see Fig. 1). Under such anti-plane mechanical and in-plane electrical loadings,only the out-of plane displacement and the in-plane electric fields are non-vanishing. The governing equations can be simplified under the condition of anti-plane strain. Therefore,we have

The relations between the electric fields and the electrical potential φ are

In this case,the constitutive equations for the piezoelectric material can be written as follows: where c₄₄(Y) is the elastic stiffness measured in a constant electric field,e₁₅(Y) is the piezoelectric constant,and ε₁₁(Y) is the dielectric which is measured at a constant strain. In the absence of body forces and free charges,the mechanical equilibrium equation and Maxwell equation for the piezoelectric material under anti-plane mechanical and in-plane electrical loadings can be expressed by where ρ(Y ) is the density of the FGP layer.

Combining Eq. (3) and Eq. (4),we can show that the governing equations can be expressed in terms of the displacement and electric potential components as follows:

where ∇² is the two dimensional Laplacian operator defined by

We focus on the special class of FGP materials,where the variations of the material properties are assumed to be exponential forms so as to obtain the analytical solutions for the equilibrium equations. Therefore,we assume that FGP materials have the following inhomogeneous properties:

where λ is constant,and c₄₄₀,e₁₅₀,ε₁₁₀,and ρ₀ are the values at the plane Y = 0. Substituting Eq. (6) into Eq. (5) yields The appropriate function is given by Bleustein^[20],which is where

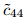Then,Eq. (7) can be rewritten as follows: where is the piezoelectric stiffened elastic constant expressed by

For the analysis of the moving crack with the constant velocity V along the X-direction, since the problem is in a steady state,it is convenient to introduce a Galilean transformation such as

where (x,y,t) is the moving coordinate system attached to the moving dislocation. In the transformed coordinate system,Eq. (9) becomes independent of the time variable t,and can be written as follows: where C_T is the speed of the transverse shear wave. The constitutive equations for piezoelectric materials can be written as follows:

In the theoretical studies of cracked piezoelectric materials,the modeling of the electric boundary conditions along the crack faces is still an open problem. Generally,there are two well-accepted electric boundary conditions,i.e.,the permeable boundary condition and the impermeable boundary condition. From the physical viewpoint,these two electric boundary conditions are two extreme cases. The permeable boundary condition represents the case where the crack faces are in complete contact,and the impermeable boundary condition represents the case where the crack is open and filled with vacuum. In the present study,the impermeable boundary condition is examined. For the impermeable case,the conditions for the screw dislocation are as follows:

where b_mz and b_p designate the dislocation Burgers vectors. Although the jump in the electric potential is not a type of dislocation,it is referred here as electric dislocation for convenience. Substituting Eq. (8) to Eq. (14),we have The Fourier transform is defined as where Applying the Fourier transform to Eq. (11),we have where

With Eq. (15),we can determine the unknown functions A_i and C_i (i = 1,2,3,4). The results are shown in Appendix A. With the aid of the constitutive equations,it is not difficult to obtain the expressions for the components of the stress and the electric displacement. For instance, we can obtain In the particular case of screw dislocation in the FGP layer,let V = 0 in the above equations. Then,we can obtain the stress and electric displacement fields as follows: where

The above solutions are identical to those reported by Mousavi and Paavola^[20]. The integrals in Eq. (19) can be evaluated with the aid of the contour integration and the residue theorem. To carry out the contour integration,we need that the integrands vanish when |ω| → ∞. Consequently,for ξ ≤ x,the contour of the integration consists of the first quadrant and the second quadrant of the complex ω-plane,while for x ≤ ξ,the contour engulfs the third quadrant and the fourth quadrant. From the above integral solution (19),the stress and electric displacement can be expressed as follows:

3 Solution of multiple moving crack problem

The distributed dislocation technique has been used by several investigators for the analyses of cracked bodies under mechanical loading^[22]. We use the solution of dislocation in the FGP strip for the analysis of strip with multiple moving cracks. Let N be the number of the moving cracks in the FGP strip. The parameter −1 ≤ s ≤ 1 is chosen. The following change of variables is employed for a crack with the length 2l. The crack configuration with respect to the coordinate system (x,y) may be described in the parametric form as follows:

where

We distribute the dislocations with unknown densities along the crack surface. The principle of superposition is invoked to obtain the traction on a given crack surface. The anti-plane traction and electric potential on the face of the ith crack due to the presence of distribution of the above mentioned dislocations on all the N cracks are obtained. The system of singular integral equations can be written as follows:

where B_mzj(t) and B_pj(t) are the dislocation densities on the non-dimensionless length of the boundary of the jth crack. With Eq. (21),we can obtain the kernels of the integral equations as follows:

By virtue of Bueckner’s principle^[23],the functions of the left-hand side of Eq. (23) are the stress components and the electric displacement at the presumed location of the cracks with negative sign. This implies impermeable crack boundary conditions. Since the stress component and the electric displacement in Eq. (19) are Cauchy singular at the dislocation location,Eq. (23) for the density functions is Cauchy singular for i = j as s → t. Employing the definition of the density function,the equations for the crack opening displacement and the electric potential across the jth crack become

The displacement field is single-valued out of the crack surfaces. Thus,the dislocation density for the jth crack is subjected to the following closure requirement:

The stress fields in the neighborhood of the crack tips behave like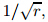 where r is the distance from the crack tip. Therefore,the dislocation densities are The parameter g_kj(t) is obtained by solving the system of Eqs. (23) and (26). The stress factor and the electric intensity factor for the ith crack in terms of the crack opening displacement and the electrical potential can be expressed as follows: where L and R designate the left tip and the right tip of a crack,respectively,and The stress and electric intensity factors for a moving crack can be defined as follows:

For brevity,the details of the derivation of the field intensity factors are not given here.

4 Numerical results and discussion

The validity of the analysis is examined by considering stationary cracks. Once the moving dislocation is simplified to the stationary case,the stress and electric displacement components (see Eq. (20)) can be simplified to those reported by Mousavi and Paavola^{[20, 21]} for the static analysis of FGP layers.

All the field variables are dependent on the crack moving velocity. In order to investigate the effects of the material properties gradient and the crack moving velocity on the field intensity factors,we carry out some numerical calculations. In the computational procedure,we consider the PZT-4 piezoelectric ceramic,whose material properties are given as follows:

The electromechanical coupling factor that we have used is defined by

As the first example (see Fig. 2),an FGP layer is considered,which is weakened by a moving straight crack on the center-line of the layer. The FGP layer is under the constant anti-plane mechanical loading

and the in-plane electrical loading

on the edges,while

Figure 2 depicts the variations of the normalized dynamic stress intensity factor versus the crack velocity for different λL. As shown in the figure,when λL increases,the dynamic stress intensity factor increases. Figure 2 also shows that the dynamic stress intensity factor increases with an increase in the crack speed. In this case,an excellent agreement is observed with the results presented by Mousavi and Paavola^[20] by letting V be zero.

Figures 3 and 4 show the normalized dynamic field intensity factors K_M/K_0M and K_D/K_0D as functions of the normalized crack location d/L. The stress intensity factor is normalized by

and the electric intensity factor is normalized by

In Fig. 3,

while the dimensionless crack velocity is taken to be

The result depicts the effects of the edge velocity and the crack velocity on the dynamic stress intensity factors. The results show that when the crack velocity increases,the stress intensity factors increase. The maximum stress intensity factor for the crack tips occurs when the distance between the crack and the edge is minimal. In Fig. 4,

while

The variation trend of the electric intensity factor remains the same when λL changes.

The variations of the normalized stress intensity factor of the crack tips K_M/K_0M versus V/CT are depicted in Fig. 5,where

is the crack length. The results show that the dynamic stress intensity factors increase with the increase in V/C_T and tend to the solutions for the stationary crack in an FGP strip as V/C_T → 0,which is also reported by Mousavi and Paavola^[20]. The maximum stress intensity factor for the crack tips R₁ and L₂ occurs when the distance between them is minimal.

In the next example (see Fig. 6),the strip contains two parallel identical moving cracks when

which are located on the center-line of the strip. Figure 6 shows the variations of the normalized dynamic stress intensity factor K_M/K_0M versus the dimensionless parameter a/h for various λL when

The results show that the crack lengths remain fixed while the centers of the cracks change with the same rate. It is readily seen from Fig. 6 that the stress intensity factor for the crack tips reduces rapidly when a/h increases.

Figure 7 shows the variations of K_D/K_0D versus the dimensionless parameter a/h. The propagation of the two cracks is parallel to the strip edges,and

The electromechanical coupling factor E_cf is taken to be 0.5. It is readily seen from Fig. 7 that, when a/h increases,the electric intensity factor for the crack tips reduces rapidly.

In the last example,two equal-length cracks which are parallel to the strip edges are shown in Fig. 8. The distance between the crack centers remains fixed,while the crack velocity changes. Figure 8 depicts the dimensionless electric stress intensity factor versus the dimensionless crack velocity when

The results show that the maximum stress intensity factor for the crack tips occurs when the crack velocity increases. Moreover,when the crack velocity is lower,the difference is significant when the crack velocity increases.

5 Conclusions

The present work deals with the dynamic behavior of an FGP layer containing multiple moving cracks subjected to electro-mechanical loadings. The analytical approach is based on the use of the dislocation method. Numerical calculations are carried out to study the effects of the geometry of the moving cracks and the material properties on the resulting dynamic stress intensity factor and the electric displacement intensity factor. The obtained results agree with the previous solutions. In summary,the dynamic stress intensity factor and the electric displacement intensity factor depend on the critical factors such as the crack velocity,the distance of the crack tip from the boundaries of the FGP layer,and the material properties. Furthermore,in all examples,it is observed that the stress fields in the FGP layer increase when the crack velocity increases.