Shanghai University
Article Information
- Jiayu WU, Hong YUAN, Renhuai LIU. 2015.
- Theory and calculation of stress transfer between fiber and matrix
- Appl. Math. Mech. -Engl. Ed., 36(6): 815-826
- http://dx.doi.org/10.1007/s10483-015-1947-6
Article History
- Received 2014-6-23;
- in final form 2014-11-17
During the past decades,fiber reinforced polymers (FRPs) have been widely used to reinforce or strengthen structures. Among all the failure patterns of FRPs,fiber-matrix interface debonding is the most common one. The shear-lag model (SLM) was first presented by Cox in 1952[1] to predict the interfacial mechanical behavior of two-phase composites. In the earlier models,Kelly and Street[2] assumed that the shear strain matrix rate increased because of the presence of fibers,and this increase was inversely proportional to the fiber spacing. Lagoudas et al.[3] and Beyerlein and Phoenix[4] used the SLM for the composite case with visco-elastic matrix,elastic fiber,and bond interface. Outwater[5] and Nardone and Prewo[6] assumed that a perfectly visco-plastic matrix and linear shear forces were used to the fiber-matrix interface. Many scientists and researchers have paid much attention to the fracture problem of fiber-matrix pullout tests in recent years,and have obtained lots of significant conclusions. A highly recommendable review of fiber-matrix pullout test analyses was proposed by Shah and Ouyang[7]. Bazant and Desmorat[8] theoretically studied the fiber-matrix pullout test affected by the size. Yuan et al.[9] analyzed the varieties of nonlinear FRP-concrete interfacial properties,and described the pre-cracking and post-cracking (elastic,softening,debonding) behaviors. In this paper,we will discuss the fiber-matrix pullout test problem with the method proposed by Yuan et al.[9].
2 Fundamental equationsConsider a fiber pullout test from the surrounding matrix (see Fig. 1). The cylindrical fiber radius rf is assumed to be embedded in an outer cylinder radius rm. Young’s moduli of the fiber and matrix are Ef and Em,respectively. The shear modulus of the matrix is Gm,and the bond length of the adherent is L.
 |
| Fig. 1. Pull-push fiber-matrix pullout test |
Before the theoretical derivations,some assumptions are made as follows:
(i) The adherents (fiber and matrix) are linearly elastic and homogeneous.
(ii) The interface is only exposed to the shear stress.
(iii) The shear deformation does not occur in the fiber,and the normal stress in the fiber is distributed over the cross section uniformly.
According to the above assumptions,the equilibrium equations of the infinitesimal element (see Fig. 2) can be expressed as follows:
where τ is the interfacial shear stress,and Tm and Tf are the axial force in the matrix and fiber, respectively. The shear deformation will occur in the matrix (see Fig. 2). A parabolic shear stress distribution along the thickness of the matrix is assumed. Therefore,the normal stress of the fiber σf and the shear stress of the matrix τm can be written as follows: where uf represents the displacement of the fiber,t = r − rf,and tm = rm − rf. Equation (4) is derived from zero shear stress at r = rm,and the maximum shear stress locates at r = rf in the matrix where the shear stress is continuous. Then,with Hooke’s law,we can obtain the matrix shear strain γm and its axial displacement um as follows: where umi represents the displacement at r = rf in the matrix. The axial forces Tf and Tm for the fiber and matrix are The constitutive equation for the interface is The interfacial slip δ is defined as the relative displacement between the fiber and the matrix, i.e., Substituting Eqs.(2)-(10) into Eq.(1) and introducing the parameters of the interfacial fracture energy Gf and the local bond strength τf yield where A similar governing differential equation can be derived if the shear stress distribution along the thickness of the matrix is assumed to be linear. Equations (11) and (12) remain valid if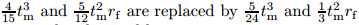 ,respectively. The shear stress in the matrix
τm
can be obtained by
Therefore,only the parabolic shear stress distributions along the thickness of the matrix are
discussed in the following.
,respectively. The shear stress in the matrix
τm
can be obtained by
Therefore,only the parabolic shear stress distributions along the thickness of the matrix are
discussed in the following.
 |
| Fig. 2. Deformation and equilibrium in infinitesimal body |
In the current study,the bilinear local bond-slip model,which consists of a linear ascending branch and a linear descending branch,is applied to the theoretical derivation of the interface fracture (see Fig. 3). Based on the model,when the value of the interfacial slip is less than δ1, the shear stress increases linearly until it reaches τf. When

 |
| Fig. 3. Local bond-slip model |
4.1 Elastic stage
There is no interfacial microcrack or macrocrack along the fiber-matrix interface under small loads. Therefore,the entire length of the interface is in an elastic state. Substituting Eq. (15) for the case when 0 ≤ δ ≤ δ1 into Eq. (11) yields
where The boundary conditions are The expressions for the slip,the interfacial shear stress,and the normal stress in the fiber can be obtained from Eq. (16) as follows: The slip at z = L is defined as the displacement of the interface,and it is denoted by Δ. According to the definition,the load-displacement relationship given by Eq. (20) is When the slip reaches δ1 at z = L,the elastic stage of the interface ends. Substituting Δ = δ1 into Eq. (20) yields the load at the beginning of the softening stage as follows: For large values of the bond length L,Eq. (24) converges to 4.2 Elastic-softening stageSoftening occurs at z = L of the interface once the interfacial slip reaches δ1. Therefore,a part of the adhesive enters the softening state,while the rest is in the elastic state. Then,the load P will increase with the increase in the length of the softening region. The ultimate load Pu first attains the end of this stage. Substituting Eq. (15) into Eq. (11) yields
where The boundary conditions and the continuity conditions are The solutions for the elastic zone of the adhesive (0 ≤ z ≤ L − a,i.e.,0 ≤ δ ≤ δ1) are and the solutions for the softening zone of the adhesive (L − a < z ≤ L,i.e.,δ1 < δ ≤ δf) are Substituting Eq. (32) into Eq. (38) yields Substituting z = L into Eq. (36) yields Obviously,the interface reaches its ultimate load at the end of this stage. P reaches its maximum when
When δ = δf at z = L,macrocracking (debonding or fracture) occurs,and then propagates along the interface. At the beginning of the macrocracking Δ = δf,the corresponding value of a,denoted by ad,can be given by Eq. (40) as follows:
For large values of L,Eq. (44) yields the following simplified form: Obviously,the debond length of the interface starting at z = L is d,and Eqs. (33)-(39) are still valid if L is replaced by (L − d). Therefore,the load-displacement relationship can be written as follows: The displacement at z = L can be obtained by solving Eq. (11) for the case when δ > δf,or, directly and more simply,by the displacement superposition along the interface. Therefore,we can obtain the following load-displacement relationship: Since τ = 0 at z = L − d,the equation relating a to d can be found from Eq. (37) as follows: Substituting Eq. (48) into Eq. (46) yields When L − d = au,the interface enters into the softening-debonding stage. Substituting au = L − d into Eq. (48) yields Moreover,Eq. (49) can be rewritten as follows: 4.4 Softening-debonding stageDuring this stage,the interface is governed by Eq. (27) with the boundary conditions
Therefore,the solution can be derived as follows: Equation (54) indicates that the length of the softening zone remains unchanged during this stage. The maximum shear stress at z=0 decreases with the load. The displacement at z = L can be derived by solving Eq. (11) for the case when δ > δf along the interface,giving the following load-displacement relationship: Next,two cases,i.e.,with and without shear deformation in the matrix,will be discussed in the next section. 5 Comparison between two casesTäljsten[11],Brosens and van Gemert[12],Wu et al.[13],Teng et al.[14],and Yuan et al.[15] analyzed the FRPs by available shear-lag methods. However,in these studies,no shear deformation in the adherents was assumed,and the normal stress within the adherents was uniformly distributed over the cross section. Subsequently,Yuan[16] improved the theoretical solutions with shear deformation in the adherents. From the analytical solution for the above fibermatrix without shear deformation,we can conclude that letting Gm equal infinity gives normal solutions without shear deformation along the thickness of the matrix. The comparison of the numerical values between the debonding process with and without shear deformation in the matrix will be discussed in the following.
In the numerical examples,the bond length L = 3 mm,the material properties and the geometry parameters are


According to the full-range behavior of the fiber-matrix debonding process discussed above, it can be clearly seen that the case without shear deformation in the matrix is a special case with shear deformation in the matrix,i.e.,Gm equals infinity.
As shown in Fig. 4,Eq. (23) implies that the displacement increases linearly with the load during the elastic stage (see the segment OA). During the elastic-softening stage,the loaddisplacement response is plotted from Eqs. (39)-(40),which is shown as the segment AB. The load-displacement curve in the elastic-softening-debonding stage is described as the segment BCD,which is obtained from Eqs. (46)-(48). Equation (56) depicts the linear load-displacement response during the softening-debonding stage of unloading as shown by the segment DE.
 |
| Fig. 4. Load-displacement response of two cases |
Based on Figs. 4 and 5,good agreements between two cases on the load-displacement curve and the shear stress value along the interface in every stage are obtained. Therefore,it can be concluded that no shear deformation in the matrix is reasonable when the full-range of shear stress propagation is analyzed and fracture processes the fiber-matrix pullout test.
Thus,only the case without shear deformation in the matrix will be discussed in the following.
 |
| Fig. 5. Interfacial shear stresses at different stages |
The effects of the bond length and Young’s modulus of fiber (matrix) on the ultimate load and the load-displacement relationship are shown in Figs. 6-9. In these figures,except for the parameter being varied,the values of all other parameters are the same as those given in the preceding section.
From Fig. 6,we can see that the load-displacement response is greatly affected by the bond length. As shown in Fig. 6,a longer bond length improves the ductility of the interface failure, and the displacement of the fiber at z = L increases rapidly,while the load remains constant at the ultimate load.
 |
| Fig. 6. Load-displacement response of three different bond lengths |
Figure 7 illustrates the relationship between the bond length and the ultimate load. From the figure,we can see that the ultimate load increases with the bond length until a certain length is reached,beyond which the ultimate load is maintained.
 |
| Fig. 7. Ultimate load with different bond lengths |
Figure 8 shows that the ultimate load increases with Young’s modulus of the fiber,while the ductility of the interface failure decreases with Young’s modulus of the fiber. Based on Eq. (13), this conclusion can also be applied to Young’s modulus of the matrix (see Fig. 9).
 |
| Fig. 8. Load-displacement response of different Young’s moduli of fiber |
 |
| Fig. 9. Load-displacement response of different Young’s moduli of matrix |
To get a deep understanding of the crack propagation and load-displacement curve along the fiber-matrix interface,ANSYS FEA simulations are implemented to simulate the behaviors of the fiber-matrix pullout test (see Fig. 10). The fiber and matrix are modeled with the linear bar element LINK8 and the solid element SOLID65,respectively. They are connected by the nonlinear combined element COMBIN39,and the simulations are performed by the displacement control method. The good agreements at the elastic stage,elastic-softening stage, and elastic-softening-debonding stage between the analytical results and the numerical results validate the model developed in the current study.
 |
| Fig. 10. Comparison of load-displacement curve between analytical results and FEA results |
In this paper,a theoretical solution of the closed form is presented to predict the fracture process of the fiber-matrix pullout test. The assumed bilinear local bond-slip model is used. The load-displacement relationship and the interfacial shear stress are obtained for four loading stages. The obtained results from the theoretical solution are convenient for a better understanding of the full-range load-displacement behavior in the fiber-matrix pullout test. While the emphasis of this paper is on the fiber-matrix pullout test,the theoretical solution can also be applied to similar tests between concrete and spindly bars of other materials. According to the results and discussion presented in the paper,the following conclusions can be drawn:
(i) The load-displacement behavior in the fiber-matrix pullout test features a linear elastic stage,a softening stage,a debonding propagation stage,and a linear unloading stage.
(ii) A longer bond length improves the ductility of the interface failure,and the displacement of the fiber at z = L increases rapidly,while the load remains constant at the ultimate load.
(iii) The ultimate load in the fiber-matrix pullout test increases with the bond length until a certain bond length is reached,and it is maintained afterwards.
(iv) The ultimate load increases with Young’s modulus of the fiber,while the ductility of the interface failure decreases with Young’s modulus of the fiber.
| [1] | Cox, H. L. The elasticity and strength of paper and other fibrous materials. British Journal of Applied Physics, 3, 72-79 (1952) |
| [2] | Kelly, A. and Street, K. N. Creep of discontinuous fibre composites, II: theory for the steady-state. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 328, 283-293 (1972) |
| [3] | Lagoudas, D. C., Phoenix, S. L., and Hui, C. Y. Time evolution of over-stress profiles near broken fibers in a composite with a viscoelastic matrix. International Journal of Solids and Structures, 25, 45-66 (1989) |
| [4] | Beyerlein, I. J. and Phoenix, S. L. Time evolution of stress redistribution around multiple fiber breaks in a composite with viscous and viscoelastic matrices. International Journal of Solids and Structures, 35, 3177-3211 (1998) |
| [5] | Outwater, J. O. The mechanics of plastics reinforced in tension. Modern Plastics, 33, 56-65 (1956) |
| [6] | Nardone, V. C. and Prewo, K. M. On the strength of discontinuous silicon carbide reinforced aluminum composites. Scripta Metallugica et Materialia, 20, 43-48 (1986) |
| [7] | Shah, S. P. and Ouyang, C. Mechanical behavior of fiber-reinforced cement-based composites. Journal of the American Ceramic Society, 74, 2947-1953 (1991) |
| [8] | Bazant, Z. P. and Desmorat, R. Size effect in fiber or bar pullout with interfacial crack in slip. Journal of Engineering Mechanics, 120, 1945-1962 (1994) |
| [9] | Yuan, H., Wu, Z. S., and Yoshizawa, H. Theoretical solutions on interfacial stress transfer of externally bonded steel/composite laminates. Journal of Structural Mechanics and Earthquake Engineering, 18, 27-39 (2001) |
| [10] | Yuan, H., Teng, J. G., Seracino, R., Wu, Z. S., and Yao, J. Full-range behavior of FRP-to-concrete bonded joints. Engineering Structures, 26, 553-565 (2004) |
| [11] | Täljsten, B. Strengthening of concrete prisms using the plate-bonding technique. International Journal of Fracture, 82, 253-266 (1996) |
| [12] | Brosens, K. and van Gemert, D. Plate end shear design for external CFRP laminates. Proceedings of FRAMCOS-3, Aedificatio Publishers, Freiburg, 1793-1804 (1998) |
| [13] | Wu, Z. S., Yuan, H., and Niu, H. Stress transfer and fracture propagation in different kinds of adhesive joints. Journal of Engineering Mechanics, 128, 562-573 (2002) |
| [14] | Teng, J. G., Chen, J. F., Smith, S. T., and Lam, L. FRP Strengthened RC Structures, Wiley, Chichester (2002) |
| [15] | Yuan, H., Lu, X. S., Hui, D., and Feo, L. Studies on FRP-concrete interface with hardening and softening bond-slip law. Composite Structures, 94, 3781-3792 (2012) |
| [16] | Yuan, H. Improved theoretical solutions of FRP-to-concrete interfaces. Proceedings of International Symposium on Bond Behaviour of FRP in Structures (BBFS 2005), The Hong Kong Polytechnic University, Hong Kong, 97-102 (2005) |
| [17] | Wang, H. W. Experimental and Theoretical Study on the Interfacial Bonding Strength of the Glass-Fiber/Polymer Matrix Composites (in Chinese), M. Sc. dissertation, Wuhan University of Technology, 42 (2003) |
 2015, Vol. 36
2015, Vol. 36








































