Shanghai University
Article Information
- A. M. SIDDIQUI, H. ASHRAF, A. WALAIT, T. HAROON. 2015.
- On study of horizontal thin film flow of Sisko fluid due to surface tension gradient
- Appl. Math. Mech. -Engl. Ed., 36(7): 847-862
- http://dx.doi.org/10.1007/s10483-015-1952-9
Article History
- Received 2014-10-25;
- in final form 2014-12-13
2. Department of Mathematics, COMSATS Institute of Information Technology, Islamabad 56180, Pakistan
The thin film flow of liquids due to the surface tension gradient on a moving solid object is of fundamental importance in many industrial and engineering problems. Surface tension gradient driven flow occurs in coating,levelling of paint films,mold filling,soldering,gluing, lubricating,film cooling,and boiling heat transfer[1, 2, 3, 4]. In all these examples,the repetitive feature is that when a fluid is disposed to a moving solid object (a moving horizontal plate), the fluid film moves along the plate with the velocity of the plate. Typically,such a fluid film consists of an extent of liquid bounded by the plate and the liquid-air (non-isothermal gas) interface. The fluid film flowing along the moving plate is opposed by the surface tension gradient (as a result of non-isothermal gas at the interface),which at a certain point called “stationary point” overcomes the flow of film. Once the stationary points are reached,the fluid film begins to flow on the plate in the opposite direction under the action of surface tension gradient. The film thickness δ is much shorter so that the flow takes place mainly in the longer dimension,and the component of velocity perpendicular to the plate is much smaller than that of the main flow velocity along the plate. Therefore,flow is considered to be one-dimensional. We shall consider the particular example of the motion of the thin Sisko fluid film on an infinity long horizontal moving plate,which can be extended to any frame of coatings and lubrication process[5].
In recent years,the flow of non-Newtonian fluids has gained considerable attention because of its promising applications in various fields of engineering,technology,biosciences,particu- larly in material processing,geophysics,chemical,nuclear industry,food industry,and polymer processing. Drilling mud,tooth paste,greases,polymer melts,cement slurries,paints,blood, clay coatings,etc.,are some examples of non-Newtonian fluids. It is difficult to construct a model for such a broad and complex class of fluids that can singly handily describe all the properties of non-Newtonian fluids. Therefore,several constitutive equations have been pro- posed to characterize and predict the physical structure and behavior of such fluids for different materials[6].
The flow characteristics of the above mentioned fluids include shear-thinning,shear- thickening,viscoplasticity,viscoelasticity,etc.,which are usually analyzed with the help of a power law model. Some of these flow characteristics were not fully described by the power law model. In view of this situation,Sisko proposed a constitutive equation (named after him “Sisko fluid model”) which includes Newtonian and power law fluids as a special case to char- acterize these types of flows. The Sisko fluid model is capable of describing shear thinning and shear thickening phenomena and have many important and well known industrial applications. The flow of greases at low shear rates having high viscosities and at high shear rates having low viscosities can be appropriately described by this model. Waterborne coatings and metallic automotive basecoat where polymeric suspensions are used,cement slurries,lubricating greases, most psueodoplastic fluids,and drilling fluids are some of its applications in industry[7, 8, 9, 10].
Over the years,analytical techniques have proven to be valuable tools to understand the complexity of non-Newtonian fluids. Numerous techniques such as the perturbation method (PM),the Adomian decomposition method (ADM),the variational iteration method (VIM),the homotopy analysis method (HAM),the optimal homotopy analysis method (OHAM),the ho- motopy perturbation method (HPM),and the optimal homotopy perturbation method (OHPM) have been developed to find the approximate solutions of the problems involving non-Newtonian fluids. These techniques have found profuse applications in industry and technology. Recently, the ADM[11] has proven to be a valuable alternative analytic tool for solving linear,nonlinear ordinary as well as partial differential equations,which occur in engineering and applied sci- ences. This method does not require any small parameter,linearization,perturbation,or other similar restrictions. Rather,it provides a direct scheme. An advantage of this method is that it provides infinite convergent series solutions. Each component of the series solution can easily be determined by the recursion. Hosseini and Nasabzadeh[12] discussed the fast convergence of the ADM solution. Good approximation from the first few computed terms of the series solution is obtained with high degree of accuracy as compared with other techniques[13, 14, 15, 16]. As in our case,for the horizontal thin film flow of Sisko fluid due to the surface tension gradient, the exact solution of the problem seems to be difficult. For the solution purpose,we use the truncated number of terms.
The aim of the present theoretical analysis is to find the analytic solution of the steady thin film flow of the Sisko fluid due to the surface tension gradient on a horizontally moving plate. We extend the work from Papanastasiou[1] for the Sisko fluid model and present its analytic solution using the ADM. We shall find important physical quantities including the pressure profile,the velocity profile,the maximum residue time,the locations of the stationary points, the volume flow rate,the average film velocity,the uniform film thickness,the shear stress, the surface tension profile,and the vorticity vector. We shall also observe the influence of the fluid behavior index n,the inverse capillary number C,and the Sisko fluid parameter β on the velocity of the Sisko fluid film and the surface tension profile via graphs and the influence on the velocity of the Sisko fluid film,the locations of the stationary points,the shear stress,and the vorticity vector via tables.
The remaining paper is organized in six sections. The basic governing equations and the constitutive equation for the incompressible Sisko fluid model are given in Section 2. The formulation of the problem is provided in Section 3. Section 4 includes the solution of the problem using the ADM and physical quantities such as the pressure profile,the velocity profile, the maximum residue time,the stationary points,the volume flow rate,the average film velocity, the uniform film thickness,the shear stress,the surface tension profile,and the vorticity vector. The influence of various available parameters is discussed via graphs and tables in Section 5. Concluding remarks are presented in Section 6. 2 Fundamental equations
The basic equations that govern the motion of an incompressible fluid neglecting the thermal effects are
where V is the velocity vector,ρ is the constant fluid density,f is the body force per unit mass, p is the dynamic pressure,S is the extra stress tensor,and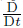 is the material time derivative.
The constitutive equation for the incompressible Sisko fluid[7, 8, 9, 10] is given by
where a and b are the material constants,and n is the fluid behavior index. If a = 0,the
equations reduce to the power law fluid model. If b = 0,the equations for the Newtonian fluid
are obtained,and A1 is the Rivlin-Ericksen tensor,
in which the superscript T denotes the transpose,and ∇V is the velocity gradient.
3 Problem formulation
is the material time derivative.
The constitutive equation for the incompressible Sisko fluid[7, 8, 9, 10] is given by
where a and b are the material constants,and n is the fluid behavior index. If a = 0,the
equations reduce to the power law fluid model. If b = 0,the equations for the Newtonian fluid
are obtained,and A1 is the Rivlin-Ericksen tensor,
in which the superscript T denotes the transpose,and ∇V is the velocity gradient.
3 Problem formulation
We consider the steady,parallel,and laminar flow of an incompressible Sisko fluid film on
a horizontally moving plate at the velocity U to the left. We choose a xOy-coordinate system
in the schematic diagram of the problem (see Fig. 1). In the diagram,we take the x-axis along
the plate and the y-axis normal to the plate. On the top,a shear stress gradient σ′ =  is applied on the interface due to the non-isothermal gas. The surface tension σ(x) increases from
left to right as shown in Fig. 1. We assume that the fluid completely wets the plate,there is
no applied (force) pressure driving the flow,and fluid flow is only due to the surface tension
gradient. Therefore,the only velocity component is in the y-direction. Accordingly,we assume
that
is applied on the interface due to the non-isothermal gas. The surface tension σ(x) increases from
left to right as shown in Fig. 1. We assume that the fluid completely wets the plate,there is
no applied (force) pressure driving the flow,and fluid flow is only due to the surface tension
gradient. Therefore,the only velocity component is in the y-direction. Accordingly,we assume
that
 |
| Fig. 1. Horizontal film flow of Sisko fluid induced by nonuniform surface tension |
The momentum balance (2) with the help of Eq. (5) and assumptions we made results in
and For the horizontal flow gx = 0,we have Integrating Eq. (8),between the interface of Sisko fluid film and non-isothermal gas at y = δ (where the pressure is pair) and an arbitrary location y (where the pressure is p),we get which leads to where f(x) is an arbitrary function. By invoking the boundary condition p = pair at y = δ in Eq. (11),we can easily show that ∀x,f(x) = 0. Hence,the pressure distribution along the Sisko fluid film in contact with air is which shows that p ≠ p(x). In view of this result,we may substitute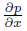 = 0 in Eq. (9) and can conclude that p = p(y) only. We have
along with the associated boundary conditions
= 0 in Eq. (9) and can conclude that p = p(y) only. We have
along with the associated boundary conditions
Integrating Eq. (13) with respect to y and then using the boundary condition (15),we get
Equation (16) with the help of Eq. (6) leads to Introduce the following dimensionless parameters:

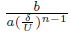 is the Sisko fluid parameter,and C =
is the Sisko fluid parameter,and C = 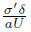 is the inverse capillary number (i.e.,the ratio of surface tension to viscous forces).
is the inverse capillary number (i.e.,the ratio of surface tension to viscous forces).
Equation (18) is a first-order nonlinear ordinary differential equation whose exact solution seems to be obtained difficultly. In the next section,we apply the ADM to solve Eq. (18) subject to the boundary condition (19). 4 Solution using ADM
We rewrite Eq. (18) in the operator form as suggested by Adomian[11],
where Ly =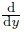 is a linear operator,which is easily invertible. N(u) represents the nonlinear term
is a linear operator,which is easily invertible. N(u) represents the nonlinear term 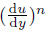 . Since Ly is invertible,we define the inverse operator Ly−1 by
. Since Ly is invertible,we define the inverse operator Ly−1 by


Putting the components u0(y),u1(y),u2(y),and u3(y) from Eqs. (25) and (30)-(32) into the decomposition series (22),we get the ADM solution of Eq. (18) in the form of
which represents the velocity profile for the thin film flow of the Sisko fluid due to the surface tension gradient on a horizontally moving plate. Using the perturbation method,we obtain the first three terms of the series solution (33).Remark 1 If we put β = 0 in Eq. (33),we retrieve the Newtonian solution[1]. Back substituting

Case 1 When σ = σ0 (where σ0 is taken as the reference surface tension at the y-axis) and U ≠ 0,Eq. (33) becomes
Equation (35) shows the plug flow of the Sisko fluid film (a solid body translation with the velocity U only).Case 2 When σ ≠ σ0 and U = 0,Eq. (33) leads to
which shows the drag flow of the Sisko fluid film due to the surface tension gradient σ′.Case 3 When σ = σ0 and U = 0,Eq. (33) results in
which corresponds to the condition of static equilibrium. Suppose that a chemical reaction, reactant A to product B,takes place in the Sisko fluid film during the flow due to surface tension gradient σ′. The maximum conversion of reactant A to product B occurs for the maximum residue time t, Using the velocity profile (34) into Eq. (38),we get which represents the maximum residue time at which the maximum conversion during a chemi- cal reaction occurs (i.e.,more reactant A reacts to give the maximum product B). In this case, reaction will be in the forward direction.The velocity profile (33) is composed of two parts,i.e.,one part is due to the motion of the plate,whereas the other part is due to the non-isothermal gas which at the interface exerts the surface tension gradient on the Sisko fluid film. Mathematically,
where up(y) and us(y) represent the velocities of the Sisko fluid film due to the motion of the plate and due to the surface tension gradient,respectively. There must exist a point y0 named as the stationary point,where which with the help of Eqs. (40) and (41) yields which provides the location where stationary points for the Sisko fluid film lie in the domain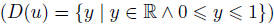 . Putting β = 0 in Eq. (43),one gets the location of stationary
points for the Newtonian fluid film,
Equation (44) infers that the stationary points lie in the domain only if C ≥ 1. If C = 1,then
the stationary points lie at the interface of non-isothermal gas (which exerts the surface tension
gradient) and the Sisko fluid film. In the dimensionless form,the flow rate Q and the average
film velocity u are defined by
which in turn,upon using Eq. (33) yields
. Putting β = 0 in Eq. (43),one gets the location of stationary
points for the Newtonian fluid film,
Equation (44) infers that the stationary points lie in the domain only if C ≥ 1. If C = 1,then
the stationary points lie at the interface of non-isothermal gas (which exerts the surface tension
gradient) and the Sisko fluid film. In the dimensionless form,the flow rate Q and the average
film velocity u are defined by
which in turn,upon using Eq. (33) yields
Putting β = 0 in Eq. (46),we retrieve the Newtonian case[1]. Now,we shall use the situation in which there is no net flow of fluid,i.e.,as much fluid is being carried by the plate to the left as is flowing due to the surface tension gradient to the right. By investigating this situation, we will be able to calculate the uniform film thickness of the Sisko fluid. By making use of the zero net flow condition,one gets
Equation (47) can be written in the dimensional form as follows: Equation (48) upon solving for the uniform film thickness δ leads to For b = 0,Eq. (49) provides the uniform film thickness of the Newtonian fluid.In the dimensionless form,the shear stress (6) exerted by the moving plate on the fluid film is given by
where


This section presents the effects of the inverse capillary number C,the Sisko fluid parameter β,and the fluid behavior index n on the results obtained in the previous section. We display some of the important results through graphs and tables.
Table 1 represents the velocity distribution of the horizontal thin film flow of the Sisko fluid due to the surface tension gradient for the inverse capillary number C,the fluid behavior index n,and the Sisko fluid parameter β. It is depicted from this table that the velocity of the Sisko fluid film due to the motion of the plate decreases until the stationary points are reached. Once the stationary points are reached,the film flow due to the surface tension gradient begins,which increases within the domain,∀y ∈ [0, 1]. It is evident from this table that,the velocity of the horizontal thin film is composed of two parts. One part of the velocity is due to the motion of the plate,whereas the other part is due to the non-isothermal gas which at the interface exerts the surface tension gradient on the Sisko fluid film. The shear thickening fluid film has a greater velocity in magnitude than the shear thinning fluid film near the plate,whereas a vice versa behavior can easily be seen near the interface. Moreover,this table discloses that the velocity of the Sisko fluid film is smaller in magnitude compared with the Newtonian fluid film. This is because of the fact that the surface tension gradient has notably more influence on the Newtonian fluid film.
 |
Figures 2-4 are drawn to show the effects of the fluid behavior index n,the inverse capillary number C,and the Sisko fluid parameter β,respectively,on the velocity profile of the horizontal thin film flow of the Sisko fluid. From Fig. 2,we depict a decrease in the horizontal film flow velocity with an increase in n. It is also seen that the shear thinning fluid film (when n = 0.4 and n = 0.7) moves faster than the shear thickening fluid film (when n = 1.3 and n = 1.6) under the influence of the surface tension gradient. This indicates that the rheology of the fluid has significant effects on the thin film flow. Figure 3 infers an increase in the horizontal film flow velocity with an increase in C. The increase in the velocity with an increase in C is due to an increase in the surface tension (with increasing C),which in turn results in an increase in the surface tension gradient on the Sisko fluid film. The horizontal film flow velocity increases with an increase in the surface tension gradient. Moreover,it is also seen that the inverse capillary number C has more impact on the shear thinning fluid film (when n=0.7) than on the shear thickening fluid film (when n=1.3). A decrease in the horizontal film flow velocity with increasing β is delineated from Fig. 4. The decrease in the velocity with an increase in β is due to the reducing effect of the surface tension gradient on the fluid film. Furthermore, the comparison of the Newtonian fluid film (β = 0) and the Sisko fluid film (β > 0) shows a notable increase in magnitude of the velocity from the Sisko fluid film to the Newtonian fluid film. A notable increase in magnitude of the velocity is the clear evidence of the influence of surface tension gradient,which shows that the Newtonian fluid film bears more than the Sisko fluid film.
 |
| Fig. 2 Effect of various values of fluid behavior index n on velocity profile when C = 3.4 and β = 0.1 |
 |
| Fig. 3 Effect of various values of inverse capillary number C on velocity profile when β = 0.1 |
 |
| Fig. 4 Effect of various values of Sisko fluid parameter β on velocity profile when C = 3.4 |
The effect of the inverse capillary number C on the horizontal thin film flow of the Newtonian fluid is shown in Fig. 5. An increase in the velocity with an increase in C is inferred.
 |
| Fig. 5 Effect of various values of inverse capillary number C on velocity profile when β = 0 |
The effects of the fluid behavior index n,the inverse capillary number C,and the Sisko fluid parameter β are observed on the surface tension profile of the horizontal thin film flow of the Sisko fluid in Figs. 6-8,respectively. From Fig. 6,it is evident that the surface tension decreases with an increase in n. The shear thinning fluid film (when n = 0.4 and n = 0.7) bears more surface tension than the shear thickening fluid film (when n = 1.3 and n = 1.6),which is again the evidence of the rheological effects of the Sisko fluid.
 |
| Fig. 6 Effect of various values of fluid behavior index n on surface tension profile when C = 3.4 and β = 0.1 |
In Fig. 7,we observe that when the value of C increases,the surface tension also increases, which indicates that the surface tension dominates over the viscous forces.
 |
| Fig. 7 Effect of various values of inverse capillary number C on surface tension profile when β = 0.1 |
From Fig. 8,we note the decrease in the surface tension with an increase in β,which is the indication of viscous forces dominance over the surface tension. We depict the inverse behavior of surface tension,i.e.,in the case of the shear thinning fluid film (when n = 0.7),we observe the increase in the surface tension with an increase in β,whereas the vice versa behavior is shown by the shear thickening fluid film (when n = 1.3). The vice versa behavior is the clear indication of shear thinning and shear thickening fluids characteristics of the Sisko fluid. We also depict that the shear thinning fluid film bears greater amount of surface tensions than the Newtonian fluid film. However,the Newtonian fluid film bears more surface tensions than the shear thickening fluid film. Evidence of the greater influence of the surface tension on the Newtonian fluid film than on the Sisko fluid film is seen.
 |
| Fig. 8 Effect of various values of Sisko fluid parameter β on surface tension profile when C = 3.4 |
Tables 2 and 3 provide the locations of the stationary points for the horizontal thin film flow of the Sisko fluid. Table 2 is tabulated to demonstrate the effect of the inverse capillary number C on the locations of the stationary points. It is noted that with the increase in C,the stationary points are shifted towards the moving plate. Table 3,which is tabulated to observe the effect of the Sisko fluid parameter β renders that,the increase in β results in shifting of the stationary points towards the interface of the Sisko fluid film and non-isothermal gas. On closer observation (Tables 2 and 3),we disclose that the stationary points of the shear thinning fluid film are located within the moving plate as compared with the shear thickening fluid film. It is also observed that the stationary points of the Newtonian fluid film lie closer to the moving plate as compared with the stationary points of the Sisko fluid film. Physics behind the shifting of stationary points towards the moving plate is the increasing effect of the surface tension gradient on the fluid film with an increase in C. Shifting of the stationary points towards the interface with increasing β is due to the decreasing effect of the surface tension gradient on the fluid film. The Newtonian fluid film bears more surface tension gradients,which is the reason why the stationary points of the Newtonian fluid film lie near the moving plate.
We tabulate Table 4 to observe the effect of the inverse capillary number C on the shear stress exerted by the moving plate on the Sisko fluid film. It is evident from this table that the shear stress increases with an increase in C. The increase in the shear stress on the fluid film is due to the increasing effect of the surface tension gradient with an increase in C. We also note that the moving plate exerts more shear stresses on the shear thinning fluid film as compared with that on the thickening fluid film. The Newtonian fluid film experiences greater amounts of shear stresses as compared with the Sisko fluid film.
Table 5 shows the distribution of the vorticity vector. In this table,we observe the effect of the inverse capillary number C. It is observed that the increase in C results in an increase in the vorticity vector in a similar way as the velocity of the fluid film. Negative sign indicates that the Sisko fluid film has clockwise rotational effects. The comparison between the shear thinning fluid film and the shear thickening fluid film discloses that the shear thinning fluid film has more rotational effects. The vorticity effect for the Newtonian fluid film is found much greater than that for the Sisko fluid film.
The present research analytically solves the steady thin film flow of the Sisko fluid on a horizontal moving plate due to the surface tension gradient. Physical expressions,such as the pressure profile,the velocity profile,the residue time,the stationary points,the volume flow rate,the average film velocity,the uniform film thickness,the shear stress,the surface tension profile,and the vorticity vector,are derived. We specify the conditions for the stationary points and the uniform film thickness and discuss three cases for the velocity profile (i) when σ = σ0 and U ≠ 0,(ii) when σ ≠ σ0 and U = 0,and (iii) when σ = σ0 and U = 0. The influence of the fluid behavior index n,the inverse capillary number C,and the Sisko fluid parameter β on the velocity profile and the surface tension profile is discussed through graphs. Tabular representations of velocity profile,stationary points,shear stress,and vorticity vector are also presented. From the interpretation of graphs and tables,we conclude
(i) The velocity of the Sisko fluid film due to the motion of the plate decreases until the stationary points are reached. Once the stationary points are reached,the film flow due to the surface tension gradient begins,which increases within the domain,∀y ∈ [0, 1]. The velocity increases with an increase in the surface tension gradient.
(ii) The velocity of the Sisko fluid film increases with an increase in the inverse capillary number C.
(iii) A decrease in the surface tension with the increasing Sisko fluid parameter β causes reduction in the surface tension gradient,which in turn reduces the velocity of the Sisko fluid film.
(iv) Stationary points lie within the domain 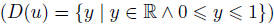 only if C ≥ 1.
At C = 1,the stationary points lie at the interface. With the increase in the inverse capillary
number C,the stationary points are shifted towards the moving plate,and vice versa locations
for the stationary points with the increasing Sisko fluid parameter β are found.
only if C ≥ 1.
At C = 1,the stationary points lie at the interface. With the increase in the inverse capillary
number C,the stationary points are shifted towards the moving plate,and vice versa locations
for the stationary points with the increasing Sisko fluid parameter β are found.
(v) The shear stress increases with the increasing inverse capillary number C.
(vi) The increase in the clockwise rotational effects for the Sisko fluid film with the increase in the inverse capillary number C is observed.
(vii) Comparison of the physical quantities discussed for the Sisko fluid film is also made with the Newtonian fluid film.
Acknowledgements The authors thank the reviewers for their valuable suggestions and comments.
| [1] | Papanastasiou, T. C. Applied Fluid Mechanics, PTR Prentice Hall, Inc., Englewood Cliffs, 309-310 (1994) |
| [2] | Howell, P. D. Surface tension driven flow on a moving curved surface. Journal of Engineering Mathematics, 45, 283-308 (2003) |
| [3] | Zhang, N. Surface tension-driven convection flow in evaporating liquid layers. Research Signpost, Trivandrum, Kerala, 147-170 (2006) |
| [4] | Levich, V. G. and Krylov, V. S. Surface tension driven phenomena. Annu. Rev. Fluid Mech., 1, 293-316 (1969) |
| [5] | O' Brien, S. B. G. and Schwartz, L. W. Theory and modeling of thin film flows. Encyclopedia of Surface and Colloid Science, Marcel Dekker, New York (2002) |
| [6] | Myers, T. G. Application of non-Newtonian models to thin film flow. Physical Review E, 72, 066302 (2005) |
| [7] | Sisko, A. W. The flow of lubricating greases. Industrial and Engineering Chemistry Research, 50(12), 1789-1792 (1958) |
| [8] | Siddiqui, A. M., Ansari, A. R., Ahmad, A., and Ahmad, N. On Taylor's scraping problem and flow of a Sisko fluid. Mathematical Modeling and Analysis, 14(4), 515-529 (2009) |
| [9] | Mekheimer, K. S. and El-Kot, M. A. Mathematical modelling of unsteady flow of a Sisko fluid through an anisotropically tapered elastic arteries with time-variant overlapping stenosis. Applied Mathematical Modelling, 36, 5393-5407 (2012) |
| [10] | Siddiqui, A. M., Hameed, A., Haroon, T., and Walait, A. Analytic solution for the drainage of Sisko fluid film down a vertical belt. Applications and Applied Mathematics, 8(2), 465-480 (2013) |
| [11] | Adomian, G. Analytical Solutions for Ordinary and Partial Differential Equations, Center for Applied Mathematics, University of Georgia, Georgia (1987) |
| [12] | Hosseini, M. M. and Nasabzadeh, H. On the convergence of Adomian decomposition method. Applied Mathematics and Computation, 182(1), 536-543 (2006) |
| [13] | Kamran, A. M., Rahim, M. T., Haroon, T., Islam, S., and Siddiqui, A. M. Solution of steady thin film flow of Johnson egalman fluid on a vertical moving belt for lifting and drainage problems using Adomian decomposition method. Applied Mathematics and Computation, 218(21), 10413-10428 (2012) |
| [14] | Wazwaz, A. M. Partial Differential Equations and Solitary Wave Theory, Nonlinear Physical Science, e-ISSN, Springer-Verlag, Berlin, 1867-8459 (2009) |
| [15] | Helal, M. A. and Mehanna, M. S. The tanh method and Adomian decomposition method for solving the foam drainage equation. Applied Mathematics and Computation, 190(1), 599-609 (2007) |
| [16] | Siddiqui, A. M., Hameed, M., Siddiqui, B. M., and Babcock, B. S. Adomian decomposition method applied to study nonlinear equations arising in non-Newtonian flows. Applied Mathematical Sci- ences, 6(98), 4889-4909 (2012) |
 2015, Vol. 36
2015, Vol. 36





















































