Shanghai University
Article Information
- Guodong ZHANG, Xiaojing DONG, Yongzheng AN, Hong LIU. 2015.
- New conditions of stability and convergence of Stokes and Newton iterations for Navier-Stokes equations
- Appl. Math. Mech. -Engl. Ed., 36(7): 863-872
- http://dx.doi.org/10.1007/s10483-015-1953-9
Article History
- Received 2014-05-13;
- in final form 2014-09-05
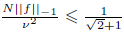 , the Stokes iteration is stable and convergent, where N is defined in the paper. When 0 < σ ≤
, the Stokes iteration is stable and convergent, where N is defined in the paper. When 0 < σ ≤ 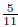 , the Newton iteration is stable and convergent. This work gives a more accurate admissible range of data for stability and convergence of the two schemes, which improves the previous results. A numerical test is given to verify the theory.
, the Newton iteration is stable and convergent. This work gives a more accurate admissible range of data for stability and convergence of the two schemes, which improves the previous results. A numerical test is given to verify the theory.
Let Ω be a bounded domain in  ,which is assumed to have the C2 boundary or be a convex polygon. We consider the stationary Navier-Stokes problem as follows:
,which is assumed to have the C2 boundary or be a convex polygon. We consider the stationary Navier-Stokes problem as follows:
For convenience,we first introduce some notations as follows:

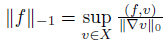 . In addition,we define two
continuous bilinear forms and a trilinear form which are
. In addition,we define two
continuous bilinear forms and a trilinear form which are
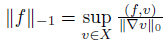
As for the above comments,the variational formulation of Problem (1) reads as follows: find (u,p) ∈ X ×M such that
Denote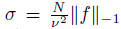 . Then,the existence and uniqueness result for Problem (4) is pretty
classical (see Refs. [6] and [14]).
. Then,the existence and uniqueness result for Problem (4) is pretty
classical (see Refs. [6] and [14]).
Theorem 1 Suppose that f ∈ X′ and υ satisfy 0 < σ < 1. Then,Problem (4) admits a unique solution pair (u,p) ∈ X ×M such that

The iterative methods are efficient for solving the stationary Navier-Stokes equations under some strong uniqueness conditions[9, 10, 25]. As we know,there are three efficient iterative schemes for solving Problem (1) as follows:
(i) Stokes iteration,
or(ii) Newton iteration,
or(Ⅲ) Oseen iteration,


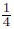 and 0 < σ ≤
and 0 < σ ≤ 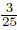 ,respectively. Besides,the Oseen scheme is unconditionally stable and convergent under 0 < σ < 1[9, 25]. Recently,
the stability and convergence condition of the Newton iteration was improved[10, 15],and the improved condition is 0 < σ ≤
,respectively. Besides,the Oseen scheme is unconditionally stable and convergent under 0 < σ < 1[9, 25]. Recently,
the stability and convergence condition of the Newton iteration was improved[10, 15],and the improved condition is 0 < σ ≤ 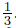 . In the present paper,using a new proof technique,we obtain
the more accurate conditions of stability and convergence of the Stokes and Newton schemes,
and the new results are 0 < σ ≤
. In the present paper,using a new proof technique,we obtain
the more accurate conditions of stability and convergence of the Stokes and Newton schemes,
and the new results are 0 < σ ≤ 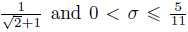 ,respectively. According to our new
theory,when
,respectively. According to our new
theory,when 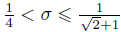 ,the Stokes iteration is still an efficient way to solve the stationary
Navier-Stokes equations. When
,the Stokes iteration is still an efficient way to solve the stationary
Navier-Stokes equations. When 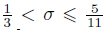 ,the Newton scheme still works. In addition,a
numerical experiment,the double-driven cavity flow problem,is presented to validate that the
Newton iteration has a larger admissible range of data than the Stokes iteration.
,the Newton scheme still works. In addition,a
numerical experiment,the double-driven cavity flow problem,is presented to validate that the
Newton iteration has a larger admissible range of data than the Stokes iteration.
The rest of this paper is organized as follows. In Section 2,we show some preliminaries playing an important role in the work. In Section 3,we present our main results of stability and convergence for the Stokes and Newton iterations. Finally,a numerical test is carried out to test our established theoretical results. 2 Preliminary
Let us consider h as a real positive parameter and Xh ×Mh characterized by Th as a finite element subspace pair of X × M ,while Th is a uniform partition of Ω into triangles K or quadrilaterals K with the diameters bounded by h. Readers can refer to Ref. [6] for details. We define


(i) There exist approximations πhv ∈ Xh and ρhq ∈ Mh for all v ∈ H2(Ω)2 ∩ X and q ∈ H1(Ω) ∩M such that
(ii) Xh ×Mh satisfies the so-called inf-sup condition as follows: for each qh ∈ Mh,there exists a positive constant β only relying on Ω and satisfying
There are several finite element spaces pairs satisfying (9) and (10)[6, 14].Define the discrete Stokes operator Ah = −PhΔh by
Throughout this paper,we denote by c and C two general positive constants only depending on Ω and (f,Ω),which may stand for different values under different circumstances. In order to obtain some estimates of the trilinear form b(·,·,·) presented in the following lemma,we bring in[17, 23] Using (12) and the Hölder inequality,we have some estimates for the trilinear form b.Lemma 1 The trilinear form b satisfies the following estimates:
The finite element Galerkin approximation of Problem (4) based on Xh ×Mh is to find (uh,ph) ∈ Xh ×Mh such that
We also learn the following stability and error estimate from Ref. [9]: 3 Main resultsIn this section,we show our main results of stability and convergence for the Stokes and Newton iterations. Denoting (en,ηn) = (uh−uhn,ph−phn),the error equations about the Stokes iteration and the Newton iteration are
respectively. First,we give the new sufficient condition of stability and convergence for the Stokes iteration in the following.
Theorem 2 Under the condition 0 < σ ≤  ,the Stokes iteration is stable and convergent,namely,for n ≥ 0,
,the Stokes iteration is stable and convergent,namely,for n ≥ 0,
Proof We first prove (19) by the method of induction. It is obvious that 
 . Setting vh = uh1,q = ph1 in (6) as n = 1 gives
. Setting vh = uh1,q = ph1 in (6) as n = 1 gives


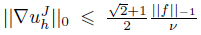 (J = 0,1,· · · ,n − 1) for n ≥ 2 and prove
(J = 0,1,· · · ,n − 1) for n ≥ 2 and prove 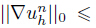
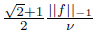 . Setting vh = uhn and q = phn in (6) gives
By the above equation,we have
Combining (25) with (27),we have
. Setting vh = uhn and q = phn in (6) gives
By the above equation,we have
Combining (25) with (27),we have

Taking vh = Ahuhn,qh = 0 in (5),using (13) and Young’s inequality,we derive

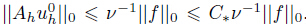 . Therefore,we suppose
. Therefore,we suppose 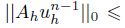
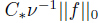 . Then,by (28),we obtain
. Then,by (28),we obtain

Taking vh=uh−uhn,qh=ph−phn in the error equation (17),using (3),(16),and (19),we have


Next,we provide the new results of stability and convergence for the Newton iteration.
Theorem 3 Under the condition 0 < σ ≤  ,the Newton iteration is stable and convergent,namely,for n ≥ 0,
,the Newton iteration is stable and convergent,namely,for n ≥ 0,
Proof We first prove (29) using the method of induction. It is evident that 
 ,and uh1 − uh0 satisfies
,and uh1 − uh0 satisfies


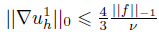 . We suppose
. We suppose 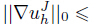
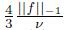 (J = 0,1,· · · ,n−1) for n ≥ 2 and prove
(J = 0,1,· · · ,n−1) for n ≥ 2 and prove 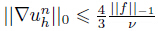 . By taking vh = uhn,qh = phn in (8) and using (3),we derive that
We know that uhn − uhn-1 satisfies
. By taking vh = uhn,qh = phn in (8) and using (3),we derive that
We know that uhn − uhn-1 satisfies



Choosing vh = Ahuhn,qh = 0 in (7),and using (13) and (14),we get

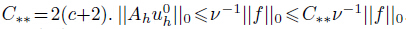 .We suppose
.We suppose 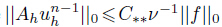 .Then,via (36),we obtain
.Then,via (36),we obtain

Taking vh = uh−uhn,qh=ph−phn in the error equation (18),by simple calculation,we have


Remark 1 From the above two theorems,we can see that the Stokes iteration is the simplest scheme among the three schemes. However,it has the least admissible range of data. The Newton iteration has a moderate admissible range of data,and it has a second-order convergent rate with respect to the iterative step. 4 Numerical example
In this section,a numerical experiment is shown. We consider the double-driven cavity flow problem presented in Fig. 1. The mini mixed finite element spaces[6] are used on grids whose mesh size is h = 1/64. The iterative schemes are designed by L2-norm of difference in successive iterations with the tolerance of 1.0×10−6. All the linear equations are solved by UMFPACK routine.
 |
| Fig. 1 Double-driven cavity flow |
Figures 2-3 describe the velocity vectors and the pressure contours with υ = 1/50 and υ = 1/100,respectively,by the usage of the Stokes iteration and the Newton iteration. We can see from Fig. 2 that the two schemes can both converge under the large viscosity υ and obtain the same numerical results. The Newton iteration consumes less time than the Stokes scheme,because the former has a second-order convergence rate with respect to the iterative step. However,when υ = 1/100,the Stokes iterative method cannot work. The Newton scheme can still solve this model (see Fig. 3). Figure 4 depicts the relationship of the iterative error with the iterative step m. We can see that,when the two scheme are both effective (υ = 1/50), the Newton iteration converges faster than the Stokes iteration. As the viscosity υ decreases (υ = 1/100),the Stokes diverges,and the Newton iteration still converges.
 |
| Fig. 2 Velocity vectors and pressure contours with υ = 1/50 |
 |
| Fig. 3 Velocity vectors and pressure contours with υ = 1/100 |
 |
| Fig. 4 Error vs. m by log-log plot |
In this paper,we obtain some more accurate conditions of stability and convergence for the Stokes and Newton iterations. For solving the stationary Navier-Stokes equations,when 0 < σ
=  ,the Stokes scheme is efficient. When 0 < σ ≤
,the Stokes scheme is efficient. When 0 < σ ≤  ,the Newton scheme is an efficient approach. In our numerical experiment,we find that the Newton scheme has a larger
admissible range of data and converges faster than the Stokes iteration,which is consistent
with our theoretical results. Unfortunately,because the values of N and
,the Newton scheme is an efficient approach. In our numerical experiment,we find that the Newton scheme has a larger
admissible range of data and converges faster than the Stokes iteration,which is consistent
with our theoretical results. Unfortunately,because the values of N and  are hard to
determine,we cannot give a method to verify the new conditions of stability and convergence
accurately. How to verify the new conditions precisely will be our future work direction in this
field.
are hard to
determine,we cannot give a method to verify the new conditions of stability and convergence
accurately. How to verify the new conditions precisely will be our future work direction in this
field.
| [1] | Ma, F. Y., Ma, Y. C., and Wo, W. F. Local and parallel finite element algorithms based on two-grid discretization for steady Navier-Stokes equations. Appl. Math. Mech. -Engl. Ed., 28(1), 27-35 (2007) DOI 10.1007/s10483-007-0104-x |
| [2] | Shang, Y. Q. and Luo, Z. D. A parallel two-level finite element method for the Navier-Stokes equations. Appl. Math. Mech. -Engl. Ed., 31(11), 1429-1438 (2010) DOI 10.1007/s10483-010- 1373-7 |
| [3] | Huang, P. Z., He, Y. N., and Feng, X. L. Two-level stabilized finite element method for Stokes eigenvalue problem. Appl. Math. Mech. -Engl. Ed., 33(5), 621-630 (2012) DOI 10.1007/s10483- 012-1575-7 |
| [4] | Chen, G., Feng, M. F., and He, Y. N. Unified analysis for stabilized methods of low-order mixed finite elements for stationary Navier-Stokes equations. Appl. Math. Mech. -Engl. Ed., 34(8), 953- 970 (2013) DOI 10.1007/s10483-013-1720-9 |
| [5] | Girault, V. and Lions, J. L. Two-grid finite element scheme for the steady Navier-Stokes equations in polyhedra. Portugal. Math., 58(1), 25-57 (2001) |
| [6] | Girault, V. and Raviart, P. A. Finite Element Methods for the Navier-Stokes Equations, Spinger- Verlag, Berlin, 278-288 (1986) |
| [7] | He, Y. N. Euler implicit/explicit iterative scheme for the stationary Navier-Stokes equations. Numer. Math., 123(1), 67-96 (2013) |
| [8] | He, Y. N. and Li, K. T. Two-level stabilized finite element methods for the steady Navier-Stokes equations. Computing, 74(4), 337-351 (2005) |
| [9] | He, Y. N. and Li, J. Convergence of three iterative methods based on the finite element discretization for the stationary Navier-Stokes equations. Comput. Methods Appl. Mech. Engrg., 198(15), 1351-1359 (2009) |
| [10] | He, Y. N. and Li, J. Numerical comparisons of time-space iterative method and spatial iterative methods for the stationary Navier-Stokes equations. J. Comput. Phys., 231(20), 6790-6800 (2012) |
| [11] | He, Y. N., Wang, A. W., Chen, Z. X., and Li, K. T. An optimal nonlinear Galerkin method with mixed finite elements for the steady Navier-Stokes equations. Numer. Methods PDEs, 19(6), 762-775 (2003) |
| [12] | Layton, W. J. A two-level discretization method for the Navier-Stokes equations. Comput. Math. Appl., 26(2), 33-38 (1993) |
| [13] | Layton, W. J., Lee, H. K., and Peterson, J. Numerical solution of the stationary Navier-Stokes equations using a multilevel finite element method. SIAM J. Sci. Comput., 20(1), 1-12 (1998) |
| [14] | Temam, R. Navier-Stokes Equations, North-Holland, Amsterdam, 158-168 (1984) |
| [15] | Xu, H. and He, Y. N. Some iterative finite element methods for steady Navier-Stokes equations with different viscosities. J. Comput. Phys., 232(1), 136-152 (2013) |
| [16] | Girault, V. and Lions, J. L. Two-grid finite element scheme for the transient Navier-Stokes problem. Math. Model. Numer. Anal., 35(5), 945-980 (2001) |
| [17] | He, Y. N. Two-level method based on finite element and Crank-Nicolson extrapolation for the time-dependent Navier-Stokes equations. SIAM J. Numer. Anal., 41(4), 1263-1285 (2004) |
| [18] | He, Y. N. and Li, K. T. Asymptotic behavior and time discretization analysis for the nonstationary Navier-Stokes problem. Numer. Math., 98(4), 647-673 (2004) |
| [19] | He, Y. N. and Sun, W. W. Stability and convergence of the Crank-Nicolson/ Adams-Bashforth scheme for the time-dependent Navier-Stokes equations. SIAM J. Numer. Anal., 45(2), 837-869 (2007) |
| [20] | Heywood, J. G. and Rannacher, R. Finite element approximation of the nonstationary Navier- Stokes problem, Ⅰ: regularity of solutions and second-order error estimates for spatial discretization. SIAM J. Numer. Anal., 19(2), 275-311 (1982) |
| [21] | Heywood, J. G. and Rannacher, R. Finite element approximations of the nonstationary Navier- Stokes problem, Ⅱ: stability of the solution and error estimates uniform in time. SIAM J. Numer. Anal., 23(4), 750-777 (1986) |
| [22] | Heywood, J. G. and Rannacher, R. Finite element approximations of the nonstationary Navier- Stokes problem, Ⅲ: smoothing property and higher order error estimates for spatial discretization. SIAM J. Numer. Anal., 25(3), 489-512 (1988) |
| [23] | Hill, A. T. and Süli, E. Approximation of the global attractor for the incompressible Navier-Stokes equations. IMA J. Numer. Anal., 20(4), 633-667 (2000) |
| [24] | Labovsky, A., Layton, W. J., Manica, C. C., Neda, M., and Rebholz, L. G. The stabilized extrapolated trapezoidal finite element method for the Navier-Stokes equations. Comput. Methods Appl. Mech. Engrg., 198(9), 958-974 (2009) |
| [25] | Li, K. T., Huang, A. X., and Huang, Q. H. Finite Element Methods and Their Applications (in Chinese), Academic Press, Beijing, 344-347 (2006) |
 2015, Vol. 36
2015, Vol. 36





























