1 Introduction

Gradient and skew-gradient systems are important for studying the integration andstability^{[1, 2]}. If a constrained mechanical system can be transformed into a gradient/skewgradientsystem,the integration and stability of the system can be discussed by the property ofthe gradient/skew-gradient system. Some results have been obtained^{[3, 4, 5, 6, 7, 8, 9, 10, 11]}. The aim of this paperis to investigate the skew-gradient representations of holonomic system,Birkhoffian system,generalized Birkhoffian system,and generalized Hamiltonian system,and to give the conditionunder which different types of systems can be represented in terms of the skew-gradient system.After transforming a dynamical system into a skew-gradient system under certain condition,the integration and stability of the system can be discussed by the property of the skew-gradientsystem. 2 Skew-gradient systems

The differential equations of motion of skew-gradient systems are^[2]

where b_ij(x) = −b_ji(x),and V = V (x). Here and hereinafter,the repeated index follows the summation convention. By generalizing the system (1) to the situation of V depending explicitly on time,we obtain the more general form In order to simplify our statement,we shall call Eq. (1) the skew-gradient system I,which is a stationary system. Equation (2) is called the skew-gradient system II,which is a non-stationary system.

The skew-gradient system I has the properties as follows^[2]:

(i) The function V = V (x) is an integration of the system (1).

(ii) If V can be a Lyapunov function,then the solution of the system (1) is stable.

The skew-gradient system II has the following properties:

(i) The function V = V (x,t) is not an integration of the system (2).

(ii) If V can be a Lyapunov function and satisfies < 0,then the solution of the system (2) is stable,because we have

3 Skew-gradient representations of holonomic systems

3.1 Differential equations of motion

The equations of motion of a general holonomic system are

where L = L(t,q,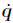) is the Lagrangian of the system,and Qs = Qs(t,q,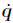) are the generalized non-potential forces. In this paper,we restrict our attention on the non-singular system,which requires the Lagrangian satisfying the regularity condition

Introducing the generalized momentum p_s and defining the Hamiltonian H as

Eq. (3) can be written as where and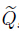 _s is the form of Q_s with the canonical variables.

If Q_s = 0,then Eq. (5) degenerates to

and then,if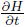 = 0,we have If 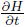= = 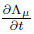0,then Eq.(5) is given by 3.2 Skew-gradient representation

The system (8) is obviously a skew-gradient system I when we take

Similarly,the system (7) is a skew-gradient system II when we select If there exists an anti-symmetric matrix (b_μυ ) and a function V = V (a) which satisfy the conditions then the system (9) can be transformed into the skew-gradient system I. In addition,if there exists an anti-symmetric matrix (b_μυ ) and a function V = V (t,a) satisfying the conditions then the system (5) can be transformed into the skew-gradient system II. 3.3 Examples of application

Example 1 Consider a two-degree-of-freedom system

where each quantity in Eq. (14) has been nondimensionalized,and we try to transform it into a skew-gradient system.

The differential equations of motion are

Let

Thus,we have

and the matrix form is

where the matrix is antisymmtric,and V is

which is an integration and a Lyapunov function of the system. Obviously,the type of this system is a skew-gradient system I. Therefore,the zero solution a¹ = a² = a³ = a⁴ = 0 is stable.

Example 2 Consider a single-degree-of-freedom system with Lagrangain

Try to transform it into a skew-gradient system.

The differential equation of motion is

Let

Thus,the first-order equations of the system are

which is a skew-gradient system II,and V is

which is positive definite in a neighborhood of a¹ = a² = 0 and satisfies

Thus,the solution a¹ = a² = 0 is stable. 4 Skew-gradient representation of Birkhoffian systems

4.1 Equations of motion

Birkhoff’s equations are^{[12, 13]}

Here,

Assume that the system (16) is nonsingular,i.e.,

Thus,all ˙aμ can be solved from (16), where 4.2 Skew-gradient representation

For the stationary Birkhoffian system,R_μ and B do not depend explicitly on time,i.e.,R_μ = R_μ(a),B = B(a). If there is an anti-symmetric matrix (b_μυ ) and a function V = V (a) which satisfy the condition

then this stationary Birkhoffian system can be transformed into the skew-gradient system I. Equation (20) is clearly satisfied. For the nonautonomous Birkhoffian system,if there exists an anti-symmetric matrix (b_μυ) and a function V = V (a) such that then this nonautonomous Birkhoffian system can be transformed into the skew-gradient system II. 4.3 Examples of application

Example 1 Consider a Birkhoffian system

which expresses Duffing’s equation. Try to transform it into a skew-gradient system.

The equations of motion according to Eq. (22) are

which is a skew-gradient system I. The function V = B is an integration and a Lyapunov function of the system. Therefore,the zero solution a¹ = a² = 0 is stable.

Example 2 The Birkhoffian functions are

Try to transform this Birkhoffian system into a skew-gradient system.

By the functions (23),Birkhoff’s equations can be obtained,

This system is a skew gradient system II. The function

is positive definite and satisfies

Thus,the solution a¹ = a² = 0 is stable. 5 Skew-gradient representations of generalized Birkhoffian systems

5.1 Differential equations of motion

The generalized Birkhoffian equations are^[14]

Here,∧_μ = ∧_μ (t,a) is an additive term. If Eq. (24) is a non-singular system,all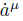 can be solved in the form of 5.2 Skew-gradient representation

For the stationary system,we have . If there exists an anti-symmetric matrix (b_μυ) and a function V = V (a) such that

then the stationary system can be transformed into the skew-gradient system I. For the nonstationary systems,if there exists an anti-symmetric matrix (b_μυ ) and a function V = V (t,a) such that then the non-stationary system can be transformed into the skew-gradient system II.

When a generalized Birkhoffian system is transformed into a skew-gradient system,the integration,especially the stability of solutions,can be studied using the properties of the skew-gradient system. 5.3 Examples of application

Example 1 A generalized Birkhoffian system is

Try to transform it into a skew-gradient system.

The generalized Birkhoff’s equations are

which can be written as

where the matrix is anti-symmetric. This system is a skew-gradient system I.

which is an integration of the system (28) and positive definite in a neighborhood of a¹ = a² = 0. Therefore,the zero solution a¹ = a² = 0 is stable.

Example 2 A generalized Birkhoffian system is

Transform it into a skew-gradient system.

The generalized Birkhoff’s equations are

which can be written as

where the matrix is anti-symmetric. This is a skew-gradient system II. V is given by

which is positive definite in a neighborhood of a¹ = a² = 0 and satisfies

Therefore,the zero solution a¹ = a² = 0 is stable. 6 Skew-gradient representation of generalized Hamiltonian system

6.1 Differential equations of motion

The generalized Hamiltonian equations are^[15]

Here,J_ij (a) = −J_ji(a),H = H (a),and ∧i = ∧i(a). By adding an addition item on the right side of Eq. (28),we obtain 6.2 Skew-gradient representation

Observably,the system (30) is a skew-gradient system I. For the system (31),if there exists an anti-symmetric matrix (b_μυ) and a function V = V (a) such that

then the system (31) is a skew-gradient system I.

For the non-stationary system,we mean that H and ∧_i depend on time t. If there exists an anti-symmetric matrix (b_μυ) and a function V = V (a) such that

then the non-stationary system can be transformed into the skew-gradient system II under the conditions. 6.3 Examples of application

Example 1 Consider the skew-gradient representation of the Euler case of the motion of rigid-body around a fixed point.

The equations of motion are in the forms of

where ω₁,ω₂,and ω₃ are the projections of the angular velocity on the inertial principal axis which is fixed together with the rigid body,and A₁,A₂,and A₃ are the principal moments of inertia of the rigid body.

Let

Then,

This is a skew-gradient system I. The function H is an integration and a positive definite function in a neighborhood of x1 = x2 = x3 = 0. Therefore,the zero solution x₁ = x₂ = x₃ = 0 is stable.

Example 2 A generalized Hamiltonian system is

Try to transform it into a skew-gradient system.

Substituting Eq. (36) into Eq. (31) yields

and the matrix form is

where the matrix is anti-symmetric. V is in the form of

which is an integration of the system. Thus,the system (36) is a skew-gradient system I. Therefore,the zero solution a¹ = a² = a³ = 0 is stable.

Example 3 A generalized Hamiltonian system is

Try to transform it into a skew-gradient system.

The differential equations of motion are

which can be written as

where the matrix is anti-symmetric,and V is in the form of

This is a skew-gradient system II. The function V is a positive definite function in a neighborhood of a¹ = a² = a³ = 0 and satisfies

Therefore,the zero solution a¹ = a² = a³ = 0 is stable. 7 Conclusions

It should be stressed here that the skew-gradient system is a kind of mathematical system.It is very effective for studying the integration of system and the stability of solution. Somedynamical systems are naturally skew-gradient systems,such as stationary Lagrangian systems,stationary Hamiltonian systems,autonomous Birkhoffian systems,and stationary generalizedHamiltonian systems. For general constrained systems,they can be skew-gradient systemsonly under certain conditions. The skew-gradient representations of four types of constrainedsystems are discussed in this paper,especially the case of non-stationary systems. Similarresearch can also be expanded to other mechanical systems.