Shanghai University
Article Information
- Lidan YU, Tianfu JIN, Zhengnan YIN, Heng XIAO. 2015.
- Multi-axial strain-stiffening elastic potentials with energy bounds: explicit approach based on uniaxial data
- Appl. Math. Mech. -Engl. Ed., 36(7): 883-894
- http://dx.doi.org/10.1007/s10483-015-1955-9
Article History
- Received 2014-07-20;
- in final form 2014-12-31
Hyper-elastic stress-strain relations of highly elastic materials such as elastomers are deriv-able from scalar functions,known as elastic potentials or elastic strain energy functions,etc.Accordingly,elastic strain energy functions represent highly elastic behaviors of rubberlike ma-terials. The forms of elastic potentials are determined based on the adequate test data. Gener-ally,such functions should be given for all possible finite deformation modes. Toward this goal,strong nonlinearities with marked dependence on deformation modes need to be treated. Fromeither the statistical or the phenomenological approach,various forms of elastic potentials havebeen derived since the 1940s. In the respect of the statistical mechanics treatment,reviewsof earlier results may be found in the monograph by Treloar[1],and some recent results werepresented by Arruda and Boyce[2],Boyce[3],Boyce and Arruda[4],Fried[5],Miehe et al.[6],Dianiand Gilormini[7],Drozdov and Gottlieb[8],Ogden et al.[9],and many others. In the respectof the phenomenological treatment,references may be made to the monographs by Ogden[10]and Saccomandi and Ogden[11] as well as the review article by Vahapoglu and Karadenitz[12].Further references will be given later on.
Most recent results from both the approaches have shown considerable progresses in furtherrepresenting the strain-stiffening effect. It is known from the experimental tests (see,e.g.,Treloar[1] and Arruda and Boyce[2]) that the stress may rapidly grow to infinity,whenever thestretch is approaching certain limits. This effect arises from the limited extensibility of longchain-like macromolecules and represents an essential feature of the nonlinear complexity ofrubberlike elasticity. Two-term elastic potentials with the strain-stiffening effect were presentedby Arruda and Boyce[2] and Gent[13] from the statistical and phenomenological approaches,separately,and shown to be in good accord with the test data at very large stretch close to 800%.Developments have been made based on these pioneering studies,and further results havebeen derived by Boyce[3],Boyce and Arruda[4],Ogden et al.[9],Horgan and Saccomandi[14, 15, 16],Beatty[17, 18],Zuniga and Beatty[19],Gent[20],Murphy[21],Zuniga[22],Horgan and Murphy[23], Zhang et al.[24, 25],and many others.
Such strain-stiffening potentials proposed in recent studies compare well with the uniaxialtension data with the stretch approaching nearly 800% and also display good correlations withthe biaxial data and others. However,there is an issue that needs to be examined. In fact,itmay be noted that,as the stretch is approaching certain limits,the elastic strain energy wouldgrow to infinity. This would imply the following consequence at variance with physical reality,namely,unbounded energy might be generated in deforming a rubberlike material.
Toward a solution to the above issue,new elastic potentials should be found to meet tworequirements in sharp contrast,namely,whenever the stretch is approaching certain limits,thestress should become unbounded,whereas,in the mean time,the strain energy should be alwaysbounded. At first sight,it does not seem that the two requirements just indicated could be metfor an elastic potential,since the strain energy,i.e.,the deformation work done by the stress,should be finite as the stress grows to infinity.
In this study,we will show that the strain-stiffening elastic potentials with energy bounds,as indicated above,may be found. Toward this objective,the new explicit approach suggestedin a most recent study[26] is first developed to obtain the multi-axial elastic potentials fromthe single-variable potentials for the uniaxial case. Then,bounded elastic potentials with thestrain-stiffening effect are presented by choosing suitable forms of uniaxial potentials. Here,themulti-axial potential is determinable solely from the uniaxial data and will be compared withthe data for other benchmark tests.
This article is organized as follows. In Section 2,a new approach is proposed to obtain themulti-axial potentials directly from the one-dimensional potentials by means of certain directexplicit procedures. In Section 3,the simple forms of uniaxial potentials are presented for thepurpose of obtaining the multi-axial strain-stiffening potentials with energy bounds based onthe results in Section 3. In Section 4,numerical examples are given in fitting a number of testdata and compared with a few representative models. Finally,relevant remarks are given inSection 5. 2 Explicit approach from uniaxial to multi-axial potentials
In this section,we will propose a new approach to obtaining multi-axial potentials directlyfrom uniaxial potentials by means of explicit procedures. This represents a development ofthe approach suggested in a recent study[26]. The main results will be derived from the proce-dures of multi-axial extension and multi-axial matching based on suitable invariants of Henckyslogarithmic strain,as shown below,separately. 2.1 Hyperelastic potential with Hencky strain
Our starting point is the hyper-elastic relation formulated in terms of Henckys logarithmic strain or Hencky strain for short. The usefulness of the Hencky strain was indicated earlier by Hill[27],and recent results for applications of the Hencky strain in finite elasticity may be found in Refs. [7],[28]-[36],and many others. Reference may also be made to a review article[37].
Let F be the deformation gradient and B = F · FT be the left Cauchy-Green tensor. The three eigenvalues and the corresponding orthonormal eigenvectors of B are designated by λr2 and nr with r = 1,2,3. Then,the Hencky strain of Eulerian type,denoted by h,is given by
In terms of an elastic potential W based on the Hencky strain h,i.e.,
the stress-strain relation for incompressible isotropic hyper-elastic materials may be given by the following direct potential relation (see e.g.,Hill[27],Fitzjerald[30],Xiao and Chen[33],and Xiao et al.[34]): with the incompressibility condition The latter means that,for incompressible deformations,the Hencky strain is traceless and coincident with its deviatoric part. The elastic potential W is an isotropic function of the Hencky strain h and hence expressible as a function of any two irreducible invariants of the Hencky strain. Each invariant of h may be given in terms of the two basic invariants In the subsequent development,the following two invariants play an essential role: The invariant ψ specifies the magnitude of Hencky strain h,whereas the invariant γ prescribes the mode of deformation. For all possible deformation modes,the value γ of falls within theinterval [−1,1]. Details may be found in Ref. [26]. In particular,the following properties may be derived: where λ is the axial stretch in the uniaxial deformation of a cylindrical bar.In terms of the two Hencky invariants given by Eqs. (6)-(7),the elastic potential as shown by Eq. (2) may be reduced to the following form:
for isotropic incompressible hyperelastic solids. Equation (10) suggests that the problem of determining the elastic potential W may be reduced to that of determining a two-variable function. In what follows,we will explain how the latter can be determined directly from the uniaxial data by means of explicit procedures. This will be done in three steps shown below. 2.2 Uniaxial potentialAt the first step,we take the uniaxial deformation mode into account. Let σ and h = ln λ be the axial true stress and the axial Hencky strain (true strain),respectively. Given sufficient data for σ and h,a one-dimensional stress-strain relation may be determined in fitting these data as follows:
Then,the elastic potential for the uniaxial case may be given as follows: It may be evident that the following relation holds true: Here,the prime stands for differentiation with respect to h. 2.3 Multi-axial extension of uniaxial potentialThe uniaxial potential given by Eqs. (11)-(12) applies to the uniaxial case only. The second step is to obtain two multi-axial potentials from this uniaxial potential. This may be done by means of a direct procedure,namely,by simply replacing the one-dimensional variable,i.e.,the axial Hencky strain h in Eq. (6),with a suitable multi-axial invariant of the Hencky strain,so that,in the uniaxial case,the multi-axial potential obtained exactly gives rise to the uniaxial potential given by Eqs. (11)-(12). The invariant ψ given by Eq. (6) is introduced just for this purpose. Hence,by replacing h in Eq. (12) by ψ and − ψ,we obtain two multi-axial potentials,
Note here that,in the uniaxial case,the latter two reduce to the uniaxial potential for uniaxial extension and compression,respectively. This fact may be deduced from the property indicated by Eq. (8). 2.4 Unified potential via multi-axial matchingAs suggested by Xiao[26],the two multi-axial potentials given by Eqs. (14)-(15) may be combined to yield a unified potential by a multi-axial matching procedure,namely,
Such a multi-axial potential in the unified form exactly produces the uniaxial potential (12) for both extension and compression. In fact,from Eqs. (8)-(9),it may be deduced that This means that,in the uniaxial case with γ = ±1,the unified potential (16) exactly yields the uniaxial potential and the derivative with respect to the invariant . However,the derivative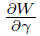 at γ = ±1 is restricted and given by (w(|h|) + w(−|h|))/2.
at γ = ±1 is restricted and given by (w(|h|) + w(−|h|))/2.
As a new development,here at the third step,we remove the above restriction for the twoderivatives 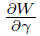 at = γ ± 1 by allowing them to be two functions,Γ+ and Γ−,for the purpose of obtaining a new multi-axial elastic potential in a broader sense. The new result is
at = γ ± 1 by allowing them to be two functions,Γ+ and Γ−,for the purpose of obtaining a new multi-axial elastic potential in a broader sense. The new result is
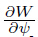 and
and 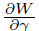 at γ = ±1. The following simple forms of the two derivatives will be taken into consideration:
where b1 and b2 are two parameters. In this case,Eq. (18) yields
2.5 Multi-axial stress-strain relation
at γ = ±1. The following simple forms of the two derivatives will be taken into consideration:
where b1 and b2 are two parameters. In this case,Eq. (18) yields
2.5 Multi-axial stress-strain relation Now with the multi-axial potential W given by Eq. (20),the multi-axial stress-strain relation is obtainable from Eq. (3). The result is given as follows:
where the deviatoric tensor k is in the form of and the coefficients ξ and η are given byIt may be clear that the results in this section reduce the problem of determining multi-axial elastic potentials to that of determining a one-dimensional elastic potential,in conjunction with two functions Γ+ and γ− specifying the two derivatives 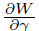 at γ = ±1. The multi-axial potential derived above can automatically match any given test data for the uniaxial case by suitably choosing the uniaxial function as shown in Eq. (11). Then,its predictions for other deformation modes may be compared with the test data for other cases. This will be done in the next section.
3 Multi-axial strain-stiffening potential with energy bounds
at γ = ±1. The multi-axial potential derived above can automatically match any given test data for the uniaxial case by suitably choosing the uniaxial function as shown in Eq. (11). Then,its predictions for other deformation modes may be compared with the test data for other cases. This will be done in the next section.
3 Multi-axial strain-stiffening potential with energy bounds
As evidenced from the test data (see,e.g.,Treloar[1] and Arruda and Boyce[2]),rubber-like materials display strain-stiffening effects. Namely,the stress tends to grow indefinitely as the stretch is approaching certain limits. A uniaxial stress-strain curve with such effects is schematically shown in Fig. 1. he and −hc in Fig. 1 are referred to as the extension limit and the compression limit,respectively. As the stretch is approaching either of the two limits,the stress grows very rapidly and goes to infinity,whereas the stress changes normally over an intermediate interval between the two limits. Although the stress becomes unbounded at either of the two limits,the strain energy does not need to be unbounded,considering the fact that the latter is given by the integration as shown by Eq. (12). Indeed,a bounded strain energy may be derived with an unlimitedly growing stress. Toward this goal,the following simple form of the uniaxial stress-strain relation is taken into account:
In the above equation,the parameter E is just Young’s modulus and characterizes the elastic behavior at the infinitesimal strain. Moreover,the dimensionless parameter α represents the growth rate of the stress at the two limits he and hc. |
| Fig. 1 Uniaxial stress-strain curve with strain-stiffening effects prior to strain limits |
It may readily be shown that the extension and compression limits he and hc are just two limiting points of the function given by Eq. (25). Now we show that the strain energy with this function is bounded. In fact,from Eqs. (12) and (25),we obtain the uniaxial strain energy as follows:
It follows from the above that the strain energy is indeed always bounded. Thus,from the uniaxial potential given by Eqs. (26) and (18),in particular,Eq. (20),we obtain a multi-axial strain-stiffening elastic potential with energy bounds. 4 Numerical examples and comparisonsIn this section,the multi-axial strain-stiffening elastic potential with energy bounds sug-gested in the last section will be compared with the test data available from the literature. 4.1 Model predictions for three deformation modes
Three simple deformation modes,including the uniaxial extension,the equi-biaxial exten-sion,and the plane-strain extension,as well as a case of general biaxial stretch are taken into consideration. The stresses and the deformation gradients for these cases are assembled below.
(i) Uniaxial extension
Here,λ and σ are the axial stretch and the axial true stress,respectively.(ii) Equi-biaxial extension
Here,λ and σ are the stretch and the true stress in the loading direction,respectively.(iii) Plane-strain extension
Here,σ1 and λ are the true stress and the stretch in the loading direction,respectively,and σ2 is the true stress in the un-deformed direction. The coefficients ξ and η are evaluated from Eqs. (23)-(24).(iv) General biaxial extension
where the coefficients ξ and η are evaluated from Eqs. (23)-(24). Moreover, In the biaxial stretch at issue,the stresses σ1 and σ2 are applied in the e1- and e2-directions,respectively,and there is no stress in the e3-direction.It should be pointed out that the test data are usually provided in terms of nominal stresses. In fitting such data,the true stresses as given in the above should be converted to their corre- sponding nominal stresses,as is the case in what follows. 4.2 Treloar’s classical data
We first consider the classical data of Treloar[1] for the uniaxial,biaxial,and plan-strain extensions. The results are shown in Fig. 2 and 3 with the following values of the parameters:

 |
| Fig. 2 Comparisons of three potentials in fitting Treloar’s classical data for uniaxial extension |
 |
| Fig. 3 Comparisons of three potentials in fitting Treloar’s classical data for equi-biaxial extension and plane-strain extension |
The four parameters E,he,hc,and α are determined in fitting the data for the uniaxial extension and the equi-biaxial extension (uniaxial compression),while the two parameters b1 and b2 are prescribed by fitting the plane-strain (shear) data. The results of the well-known Gent model[13] and the two-term potential suggested recently by Lopez-Pamies[38] are included in Figs. 2 and 3 for comparison purposes. 4.3 Nonlinear data at small stretches
Next,we turn attention to nonlinear data at small stretches. It is known that usual rubberymaterials display weakly nonlinearly elastic behavior at small stretches. However,strong non-linearity may be expected at small stretches,as evidenced from the most recent data reportedby Lahellec et al.[39] for a commercial elastomer synthesized by the tire company Michelin. Ina recent study,Lopez-Pamies[38] demonstrated that the well-known two-term models fail in fit-ting such strongly nonlinear data. As indicated by Lopez-Pamies[38],Gent’s two-term potentialmay be too restrictive to characterize the strongly nonlinear behavior of the elastomer at issue,whereas the Lopez-Pamies two-term potential[38] achieves good accord with the data. That isalso the case for the proposed potential with the following parameter values:

 |
| Fig. 4 Fitting strongly nonlinear data at small stretches in uniaxial extension |
 |
| Fig. 5 Fitting strongly nonlinear data at small stretches in plane-strain extension |
With the above study of the nonlinear data at issue,it may be worthwhile to point out a relevant fact. As seen from the study of Treloar’s data,usually the compression limit hc is much greater than the extension limit he. However,here the nonlinear data at small stretches supply an unusual example in sharp contrast,namely,the extension limit he may be greaterthan the compression limit hc. 4.4 Data for case of general biaxial stretch
Finally,we consider a case of general biaxial stretch. The data in this respect were reportedby Jones and Treloar[40]. In a rectangular sample undergone stretches in two perpendiculardirections,the stretch in one direction is set to be a fixed value given by 2.29,while the stretchin the other direction is changing. Of the six parameters,E,he,hc,and α are determined infitting the data for the uniaxial extension and the equi-biaxial extension (uniaxial compression),while b1 and b2 are prescribed by fitting the plane-strain (shear) data for the stresses in theloading direction and in the un-deformed direction,separately. The results are shown in Fig. 6 with the following parameter values:

 |
| Fig. 6 Fitting Jones and Treloar’s data for uniaxial,equi-biaxial,plane-strain,and general biaxial stretches |
In the preceding sections,the approach suggested in a newest study[26] is developed to obtainthe multi-axial strain-stiffening elastic potentials with energy bounds. With the new approach,multi-axial elastic potential may be obtained directly from uniaxial potentials by means ofexplicit procedures. It has been demonstrated that a simple form of the uniaxial potentialmay give rise to a multi-axial potential that can characterize the strain-stiffening effect and,in the meantime,ensure bounded energy,thus bypassing the issue of unbounded strain energy.Numerical examples show good accord with the test data over the whole stretch range tested. Ascompared with the other models,the new model proposed may be more suitable and convenientfor applications,in the sense that it is in better agreement with the test data and providesparameters directly related to the deformation features.
The results are derived for the incompressibility case. However,the incompressibility con- straint is merely an idealization of the deformation behavior of realistic rubberlike materials. Volumetric deformation,albeit very small,may be expected. A further study will be needed for general compressible deformations.
| [1] | Treloar, L. R. G.The Physics of Rubber Elasticity, Oxford University Press, Oxford (1975) |
| [2] | Arruda, E. M. and Boyce, M. C. A three-dimensional constitutive model for the large stretch behaviour of rubber elastic materials. J. Mech. Phys. Solids, 41, 389-412 (1993) |
| [3] | Boyce, M. C. Direct comparison of the Gent and the Arruda-Boyce constitutive models of rubber elasticity. Rubber Chem. Technol., 69, 781-785 (1996) |
| [4] | Boyce, M. C. and Arruda, E. M. Constitutive models of rubber elasticity: a review. Rubber Chem. Technol., 73, 504-523 (2003) |
| [5] | Fried, E. An elementary molecular-statistical basis for the Mooney and Rivlin-Saunders theories of rubber elasticity. J. Mech. Phys. Solids, 50, 571-582 (2002) |
| [6] | Miehe, C., Göktepe, S., and Lulei, F. A micro-macro approach to rubberlike materials-part I: the non-affine microsphere model of rubber elasticity. J. Mech. Phys. Solids, 52, 2617-2660 (2004) |
| [7] | Diani, J. and Gilormini, P. Combining the logarithmic strain and the full-network model for a better understanding of the hyperelastic behaviour of rubber-like materials. J. Mech. Phys. Solids, 53, 2579-2596 (2005) |
| [8] | Drozdov, A. D. and Gottlieb, M. Ogden-type constitutive equations in finite elasticity of elastomers. Acta Mechanica, 183, 231-252 (2006) |
| [9] | Ogden, R. W., Saccomandi, G., and Sgura, I. On worm-like chain models within the threedimensional continuum mechanics framework. Proc. R. Soc. Lond. A, 462, 749-768 (2006) |
| [10] | Ogden, R. W. Non-Linear Elastic Deformations, Ellis Horwood, Chichester (1984) |
| [11] | Saccomandi, G. and Ogden, R. W. Mechanics and Thermomechanics of Rubberlike Solids. CISM Couses and Lectures No. 452, Springer, Vienna (2004) |
| [12] | Vahapoglu, V. and Karadenitz, S. Constitutive equations for isotropic rubber-like materials using phenomenological approach: a bibliography (1930-2003). Rubber Chem. Technol., 79, 489-499 (2005) |
| [13] | Gent, A. N. A new constitutive relation for rubber. Rubber Chem. Technol., 69, 59-61 (1996) |
| [14] | Horgan, C. O. and Saccomandi, G. A molecular-statistical basis for the Gent constitutive model of rubber elasticity. J. Elasticity, 68, 167-176 (2002) |
| [15] | Horgan, C. O. and Saccomandi, G. Finite thermoelasticity with limiting chain extensibility. J. Mech. Phys. Solids, 51, 1127-1146 (2003) |
| [16] | Horgan, C. O. and Saccomandi, G. Phenomenological hyperelastic strain-stiffening constitutive models for rubber. Rubber Chem. Technol., 79, 1-18 (2006) |
| [17] | Beatty, M. F. An average-stretch full-network model for rubber elasticity. J. Elasticity, 70, 65-86 (2003) |
| [18] | Beatty, M. F. On constitutive models for limited elastic, molecular based materials. Math. Mech. Solids, 13, 375-387 (2008) |
| [19] | Zuniga, A. E. and Beatty, M. F. Constitutive equations for amended non-Gaussian network models of rubber elasticity. Int. J. Engng. Sci., 40, 2265-2294 (2003) |
| [20] | Gent, A. N. Extensibility of rubber under different types of deformation. J. Rheol., 49, 271-275 (2005) |
| [21] | Murphy, J. G. Some remarks on kinematic modeling of limiting chain extensibility. Math. Mech. Solids, 11, 629-641 (2006) |
| [22] | Zuniga, A. E. A non-Gaussian network model for rubber elasticity. Polymer, 47, 907-914 (2006) |
| [23] | Horgan, C. O. and Murphy, J. G. Limiting chain extensibility constitutive models of Valanis- Landel type. J. Elasticity, 86, 101-111 (2007) |
| [24] | Zhang, Y. Y., Li, H., Wang, X. M., Yin, Z. N., and Xiao, H. Direct determination of multi-axial elastic potentials for incompressible elastomeric solids: an accurate, explicit approach based on rational interpolation. Continuum Mech. Thermodyn., 26, 207-220 (2014) |
| [25] | Zhang, Y. Y., Li, H., and Xiao, H. A further study of rubberlike elasticity: elastic potentials matching biaxial data. Appl. Math. Mech. -Engl. Ed., 35(1), 13-24 (2014) DOI 10.1007/s10483- 014-1768-x |
| [26] | Xiao, H. An explicit, direct approach to obtaining multi-axial elastic potentials that exactly match data of four benchmark tests for rubberlike materials-part 1: incompressible deformations. Acta Mechanica, 223, 2039-2063 (2012) |
| [27] | Hill, R. Constitutive inequalities for isotropic elastic solids under finite strain. Proc. Roy. Soc. London A, 326, 131-147 (1970) |
| [28] | Anand, L. On H. Hencky's approximate strain-energy function for moderate deformations. J. Appl. Mech., 46, 78-82 (1979) |
| [29] | Anand, L.Moderate deformations in extension-torsion of incompressible isotropic elastic materials. J. Mech. Phys. Solids, 34, 293-304 (1986) |
| [30] | Fitzjerald, S. A tensorial Hencky measure of strain and strain rate for finite deformation. J. Appl. Phys., 51, 5111-5115 (1980) |
| [31] | Criscione, J. C., Humphrey, J. D., Douglas, A. S., and Hunter, W. C. An invariant basis for natural strain which yields orthogonal stress response terms in isotropic hyperelasticity. J. Mech. Phys. Solids, 48, 2445-2465 (2000) |
| [32] | Kakavas, P. A. A new development of the strain energy function for hyper-elastic materials using a logarithmic strain approach. J. Appl. Polym. Sci., 77, 660-672 (2000) |
| [33] | Xiao, H. and Chen, L. S. Hencky's logarithmic strain measure and dual stress-strain and strainstress relations in isotropic finite hyperelasticity. Int. J. Solids Struct., 40, 1455-1463 (2003) |
| [34] | Xiao, H., Bruhns, O. T., and Meyers, A. Explicit dual stress-strain and strain-stress relations of incompressible isotropic hyperelastic solids via deviatoric Hencky strain and Cauchy stress. Acta Mech., 168, 21-33 (2004) |
| [35] | Aron, M. On certain deformation classes of compressible Hencky materials. Math. Mech. Solids, 19, 467-478 (2006) |
| [36] | Horgan, C. O. and Murphy, J. G. A generalization of Hencky's strain-energy density to model the large deformation of slightly compressible solid rubber. Mech. Mater., 41, 943-950 (2009) |
| [37] | Xiao, H. Hencky strain and Hencky model: extending history and ongoing tradition. Multidiscipline Modeling in Materials and Structures, 1, 1-52 (2005) |
| [38] | Lopez-Pamies, O. A new I1-based hyperelastic model for rubber elastic materials. Comptes Rendus Mecanique, 338, 3-11 (2010) |
| [39] | Lahellec, N., Mazerolle, F., and Michel, J. C. Second-order estimate of the macro-scopic behavior of periodic hyperelastic composites: theory and experimental validation. J. Mech. Phys. Solids, 52, 27-49 (2004) |
| [40] | Jones, D. F. and Treloar, L. R. G. The properties of rubber in pure homogeneous strain. J. Phys. D, 8, 1285-1304 (1975) |
 2015, Vol. 36
2015, Vol. 36













































