1 Introduction

In 1880,the Curie brothers discovered the piezoelectric effect,that is,the ability of somecrystalline material to produce an electrical voltage proportional to the mechanical stress whichdeforms it. The deformation resulting from the application of an electric potential is thereversible effect. It was suggested by Lippman in 1881 and confirmed experimentally by theCurie. The two effects are the basis for an extensive use of piezoelectric materials in manyengineering applications such as sensors,actuators,and intelligent structures.

The electro-elastic characteristics of piezoelectric materials have been studied extensively,and their dependence on temperature is well established^{[1, 2, 3, 4, 5]}. Currently,it is interesting toincorporate the thermal effects in addition to the piezoelectric effects. This thermo-piezoelectricmodel was first proposed by Mindlin^[6] and Mig´orski^[7],and the physical laws for the thermo-piezoelectric materials were investigated by Nowacki^{[8, 9]}. Chandrasekharaiah^[10] generalizedMindlin’s theory of thermo-piezoelectricity to some special model,and Tiersten^[11] developedthe general nonlinear theory of thermo-piezoelasticity.

In the literature,there are few mathematical results dealing with contact problems involvingcoupling between mechanical and electrical properties^{[1, 2, 4, 6, 7, 12, 13, 14]} and the references therein.Up to date,no work has dealt with coupling between thermal effects and piezoelectrical proper-ties. Therefore,there is a need to extend mathematical analysis to this kind of model problems.

This work deals with a new mathematical model which describes the frictional contactbetween a thermo-piezoelectric body and a conductive foundation. The novelty of this modellies in the chosen thermo-electro-elastic behavior for the body and in the electrical and thermalconditions describing the contact. The motivation of this approach is that the thermal effects,such as thermal deformation and pyroelectric effects,are especially important for many smartceramic materials. Thus,it may be impossible to predict the electromechanical behavior withouttaking account of these thermal effects.

Here,we study a static problem of frictional contact under small deformation hypothesis,wherein the behavior of the material is modeled by a nonlinear thermo-electro-elastic consti-tutive law,and the contact is described by Signorini’s condition,Tresca’s friction law,and aregularized electrical and thermal conductivity condition. The variational formulation of thisproblem is derived,and its unique weak solvability is established.

The paper is structured as follows. In Section 2,we state the model of equilibrium processof the thermo-elctro-elastic body in frictional contact with a conductive rigid foundation. InSection 3,we introduce the notation and the assumptions on the problem data. We alsoderive the variational formulation of the problem,and the main result is stated in Theorem3.1. In Section 4,we prove the existence of a weak solution to the model and its uniquenessunder additional assumptions. The proof is based on an abstract result on elliptic variationalinequalities and fixed point arguments. 2 Mathematical model

We consider a piezoelectric body that occupies an open bounded subset Ω in 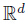(d = 2,3)with a sufficiently smooth boundary Γ = ∂Ω. This boundary is divided into three open disjointparts Γ_D,Γ_N,and Γ_C on one hand and a partition of Γ_D∪Γ_N into two open parts Γ_a and Γ_b onthe other hand,such that the two parts Γ_D and Γ_a have a nonnegative measure. The body issubjected to the action of body forces of density f₀,a volume electric charges of density q₀,anda heat source of constant strength q_t. It is also subjected to mechanical,electrical,and thermalconstraints on the boundary. Indeed,the body is assumed to be clamped in Γ_D,and thereforethe displacement field vanishes there. Moreover,we assume that a density of traction forces,denoted by f_N,acts on the boundary part Γ_N. We also assume that the electrical potentialvanishes on Γ_a,and a surface electrical charge of density q_b is prescribed on Γ_b. Finally,weassume that the temperature θ₀ is prescribed on the surface Γ_N ∪ Γ_D.

In the reference configuration,the body may come in contact over Γ_C with an electrically-thermally conductive foundation. We assume that its potential and temperature are maintainedat φ_F and θ_F. The contact is frictional,and there may be electrical charges and heat transferon the contact surface. The normalized gap between Γ_C and the rigid foundation is denotedby g.

Here and below,we do not indicate the dependence of various functions on the spatialvariable x ∈ Ω,the summation convention over repeated indices is used,and the index thatfollows a comma indicates a partial derivative with respect to the corresponding component ofthe spatial variable.

We use S^d for the linear space of second-order symmetric tensors on 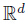and use “ · ” and 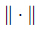to represent the inner products and the Euclidean norms on 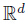and S^d,

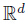We denote by u : Ω → the displacement field,σ : Ω → S^d and σ = (σ_ij ) the stress tensor,θ : Ω → 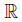the temperature,q : Ω → 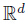and q = (q_i) the heat flux vector,and by D : Ω → Rdand D = (D_i) the electric displacement field. We also denote E(φ) = (E_i(φ)) the electricvector field,where φ : → 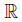is the electric potential. Moreover,let ε(u) = (ε_ij (u)) denotethe linearized strain tensor given by ε_ij(u) = 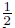(u_i,j + u_j,i),and “Div ” and “ div ” denote thedivergence operators for tensor and vector valued functions,respectively,i.e.,Div σ = (σ_ij,j )and div ξ = (ξ_j,j ). We shall adopt the usual notations for normal and tangential componentsof displacement vector and stress: v_n = v · n,v_τ = v − v_nn,σ_n = (σn) · n,and σ_τ = σn − σ_nn,where n denotes the outward normal vector on Γ.

We suppose that the process is static. The equations of stress equilibrium,the equation ofquasi-stationary electric field,and the heat conduction equation are,respectively,given by

For the linear piezoelectric material including the thermal expansion effect,we have the following constitutive relations: where ξ = (f_ijkl),ε = (e_ijk),M = (m_ij ),β = (β_ij ),and P = (p_i) are,respectively,elastic,piezoelectric,thermal expansion,electric permittivity,and pyroelectric tensors,and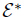 is the transpose of ε given by

where

and The Fourier law of heat conduction is given by where K = (k_ij ) denotes the thermal conductivity tensor. Next,to complete the mathematical model according to the description of the physical setting,we have the following boundary conditions: We model the frictional contact on ΓC with Signorini’s conditions and Tresca’s law and with the following regularized electrical and thermal conditions^{[13, 15]}: such that

where L is a large positive constant,δ > 0 is a small parameter,and k_e > 0 is the electrical conductivity coefficient such that the thermal conductance function k_c : r → k_c(r) is supposed to be zero for r < 0 and positive otherwise,nondecreasing and Lipschitz continuous. We note that when ψ ≡ 0,the equality (15) leads to the condition

which models the case when the foundation is a perfect electric insulator.

Similarly,we describe the case of a perfect thermally insulating foundation with

We collect the above equations and conditions to obtain the following mathematical problem.

Problem (P) Find a displacement field u : Ω → 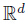,an electric potential φ : Ω → 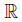,anda temperature field θ : Ω → 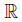such that (1)-(16) hold.

Note that if the displacement field u,the electric potential φ,and the temperature θ whichsolve Problem (P) are known,then the stress tensor σ,the electric displacement field D,andthe heat flux q can be obtained from (4)-(7). 3 Variational formulation and main result

In this section,we derive a weak formulation of Problem (P) and investigate its solvability. Everywhere in what follows we use the standard notation for the L^p spaces associated with Ω and Γ. We also use the Hilbert spaces

endowed with the inner products

Keeping in mind the boundary condition (8),we introduce the closed subspace of H₁

and the set of admissible displacements

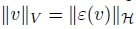Here and below,we write w for the trace γw of the function w ∈ H₁ on Γ. Since meas(Γ_D) > 0,Korn’s inequality holds where ck is a nonnegative constant depending only on and Γ_D. Therefore,the space V endowed with the inner product (u,v)_V = (ε(u),ε(v))_H is a real Hilbert space,and its associated norm is equivalent on V to the usual norm 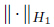. By Sobolev’s trace theorem,thereexists a constant c₀ > 0 which depends only on Ω,ΓC,and ΓD such that We also introduce the function spaces

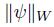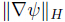Similarly,we write ζ for the trace γζ of the function ζ ∈ H¹(Ω) on Γ. Since meas(Γ_a) > 0and meas(Γ_D) > 0,it is known that W and Q are real Hilbert spaces with the inner products.(φ,ψ)W = (∇φ,∇ψ)H,and (θ,ξ)Q = (∇θ,∇ξ)H. Moreover,the associated norms = and 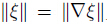are equivalent on W and Q,respectively,with the usual norms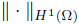. By Sobolev’s trace theorem,there exists a constant c₁ > 0 which depends only on Ω,Γ_a,and Γ_C such that and a constant c₂ > 0 which depends only on Ω,Γ_D,Γ_N,and Γ_C such that In the study of the mechanical problem (P),we need the following assumptions.

(h₁) The elasticity operator ξ : Ω × S^d → S^d,the electric permittivity tensor β = (β_ij ) : Ω × 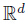→ 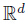,and the thermal conductivity tensor K = (k_ij ) : Ω × 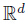→ 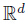satisfy the usualproperties of symmetry,boundedness,and ellipticity,

and there exists that m_ξ,m_β,m_K > 0 such that

(h₂) The piezoelectric tensor E = (e_ijk) : Ω × S_d → 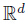,the thermal expansion tensor M= (m_ij ) : Ω × 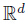→ 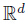,and the pyroelectric tensor P = (p_i) : Ω → 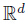satisfy

(h₃) The surface electrical conductivity ψ : Γ₃ × 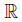→ 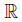⁺ and the thermal conductance k_c :Γ₃× 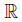→ 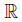⁺ satisfy the following hypothesis for π = ψ,k_c: ∃M_π > 0 such that |π(x,u)| ≤ M_π,∀u ∈ 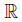,a.e. x ∈ Γ_C,and x → π(x,u) is mesurable on Γ_C for all u ∈ 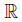and is zero for all u ≤ 0.

(h₄) The function u → π(x,u) (π = ψ,k_c) is a Lipschitz function on 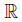for all x ∈ Γ_C.|π(x,u₁) − π(x,u₂)| ≤ L_π|u₁ − u₂|,∀u₁,u₂ ∈ 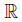,where L_π is a positive constant.

(h₅) The forces,the traction,the volume,the surface charge densities,and the strength of the heat source satisfy

(h₆) The potential and temperature of the contact surface satisfy

(h₇) The friction bound function satisfies

Next,using Riesz’s representation theorem,we define the elements f ∈ V ,q ∈ W,andq_th ∈ Q by

and we define the mappings j : V →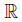 ,ℓ : V ×W² → 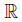,and χ : V × Q² → 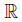by respectively.

It follows from the assumptions (h₃) and (h₆)-(h₇) that the integrals below are well-defined.

Now,by a standard variational technique,it is straightforward to see that if (u,φ,θ) satisfies the conditions (1)-(16),then

We plug (4) in (27),(5) in (28),and (7) in (29) and use E = −∇_φ to obtain the variational formulation of P in terms of displacement,electric potential,and temperature.

Problem (PV) Find a displacement field u ∈ K,an electric potential φ ∈ W,and a temperature field θ : Ω → 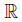such that

Now,we are able to state the following main result of existence and uniqueness.

Theorem 3.1 Assume that the assumptions (h₁)-(h₃) and (h₅)-(h₇) hold. Then,(1) Problem (PV) has at least one solution (u,φ,θ) ∈ K ×W ×Q; (2) under the assumption (h₄),there exists L^∗ > 0 such that if

then Problem (PV) has a unique solution with

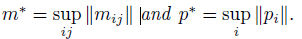
The proof of our main result will be presented in the next section. 4 Proof of main result

The proof of Theorem 3.1 will be carried out in several steps,and it is based on arguments of variational inequalities and Schauder’s fixed point theorem. To this end,we assume in the following that (h₁)-(h₃) and (h₅)-(h₇) hold.

Let K₁ and K₁ denote two closed convex sets of L²(Γ_C) as follows:

with k₁ and k₂ to be specified later,and let z = (z₁,z₂) ∈ L²(Γ_C)² be given. We define the functions

In the first step,we consider the following variational problem.

Problem (PV_z) Find a displacement field u_z ∈ K,an electric potential φ_z ∈ W,and a temperature field θ_z ∈ Q such that

The coupling system leads to considerable difficulties in the analysis of the problem. Therefore,we first solve the following thermic problem with the unknown θ_z:

To this end,using Riesz’s representation theorem,we find the element q_z ∈ Q and the operator T : Q → Q defined by Thus,Problem (PV_z^θ) can be also written in the following form: From (38),(34),(23),and (h5),it is easy to see that the linear form η → (q_z,η)Q is continuous on Q. We note that,under the assumption (h₁) on K,the operator T is linear symmetric and positive definite on Q. Moreover,T is a linear continuous invertible operator on Q,and let C = T ⁻¹. Thus,by the Lax-Milgram theorem,we conclude that (39) has a unique solution Now,we substitute θ_z = Cq_z in (35) and (36) and get where

In order to solve (41)-(42),we consider the product spaces X = V ×W and Y = (L²(Γ_C))²endowed with the inner products

and the associated norms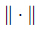 _X and 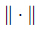_Y ,respectively. Let U = K×W be a non-empty closed convex subset of X. We also introduce the operator A : X → X and the function J : U → defined by

Keeping in mind the proprieties of the operators T ,M,and P,it follows that MC and PC are linear continuous operators. Hence,by Riesz’s representation theorem and (49),we deduce that f_z ∈ V and q_z ∈ W,then we conclude that f_z^e ∈ X.

We start by the following equivalence result.

Lemma 4.1 The pair x_z = (u_z,φ_z) ∈ U is a solution to (41)-(42) if and only if

Proof We use (ξ − φ_z) in (42) and add the corresponding inequality to (41). Then,we deduce (50). Conversely,let x_z = (u_z,φ_z) ∈ U be a solution of the elliptic variational inequality (50). By taking y = (v,φ_z) in (50),where v is an arbitrary element of K,we obtain (41). Moreover,if we take successively y = (v,φ_z + ξ) and y = (v,φ_z − ξ) in (50),where ξ is an arbitrary element of W,we will obtain (42),which finishes the proof.

We now use Lemma 4.1 to obtain the following existence and uniqueness result.

Lemma 4.2 For any z ∈ K₁ × K₂ assumed to be known,we have

(i) under the assumptions (h₁)-(h₂) and (h₅)-(h₇),(50) has a unique solution x_z = (u_z,φ_z) ∈ K ×W,and there exists c > 0 such that ;

(ii) the solution x_z of (50) depends on z ∈ Y Lipschitz continuously.

Proof We first remark that J is proper and convex on U. Moreover,by (h₇),we find thatJ is Lipschitz continuous. Therefore,it is a fortiori lower semicontinuous function. Now,weuse (h₁),(6),(47),and (45) to see that A is a strongly monotone Lipschitz continuous operatoron X,i.e.,there exists that mA,M_A > 0 such that (Ax − Ay,x − y)X > and . Since U is a non-empty closed convex set of X,by a standardresult on elliptic variational inequalities (see ^[16]),it follows that there exists a unique element(u_z,φ_z) ∈ U which satisfies (50).

Moreover,if we take y = 0 in (50),we get

As the friction coefficient S ≥ 0,we have J(x_z) ≥ 0 and thus

Taking in mind the strong monotony of A,we deduce that there exists c > 0 such that For the second part of Lemma 4.2,let us consider two given elements z = (z₁,z₂),z′ = (z′₁,z′₂ ) of Y and the associate solutions x_z ,x_z′ of (50). For all y ∈ U,we have

If we take y = x_z′ in the first inequality and y = x_z in the second one,we obtain

Hence, Furthermore,we have the following inequality:

and then Combining (52),(53),(19),and (20) yields The strong monotonicity of A,combined with (54) and (46),implies that there exists a positive constant c₃ depending on the constants c₁,c₂,m_A,m_K,m^∗,and p^∗ such that Hence,the second part of this lemma is established.

Now,we have the following result.

Lemma 4.3 For any z ∈ K₁ × K₂ assumed to be known and under the assumptions (h₁)- (h₂) and (h₅)-(h₇),the solution ∈ K ×W × Q of Problem (PV_z) depends on z ∈ Y Lipschitz continuously.

Proof We consider the product space X = X × Q endowed with the inner product

and the associated norm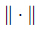 X . Now,let z = (z₁,z₂) and z′ = (z′₁ ,z′₂) be two given elements of Y and θ_z,and let θ_z′ be the corresponding solution of (39). Using the linearity of T ,we find that

It follows from (20) and (38) that

Then,

We combine the previous inequalities to see that

Lemma 4.3 is now a consequence of (58),(55),and (56).

We now use the properties (h₃) and (h₄) of the constitutive functions ψ and kc to define an operator ∧ : Y → L²(Γ_C)² by the formula

In the second step,we prove that the operator ∧ has a fixed point. To this end,we will need the following result.

Lemma 4.4 The mapping is z → = (u_z,φ_z,θ_z),where is the solution of Problem (PV_z),which is weakly continuous from Y to V ×W × Q.

Proof Let z_n = (z_1n,z_2n) be a sequence of Y which converges weakly to z = (z₁,z₂),and we denote _n = (x_zn,θ_zn) ∈ U × Q with x_zn = (u_zn,φ_zn),the solution of Problem (PV_z) corresponding to z_n. Using (38),(40),(20),and (46),we have

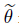Thus,the sequence (θ_zn) is bounded in Q. Then,there exists ∈ Q and a subsequence (θ_znk ) such that θ_znk ¬ 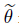. Using (39),we get Taking η = 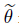± η^∗ in the previous inequality,we find According to (39) and (61),we conclude that 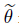is a solution of Problem (PV_z^θ). By the unique- ness of the solution of this variational equality,we deduce that 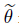= θ_z. Since θ_z is the unique limit of any subsequence (θ_znk ),we deduce that the whole sequence (θ_zn) is weakly convergent to θ_z in Q,which ensures the weak continuity of the mapping z → θ_z . Moreover,x_zn is a solution of (50) implying Now,we take y = 0 in (62) to obtain Keeping in mind (49),(43),and (44),we have

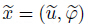Then, We also have and The strong monotonicity of A combined with (64)-(66) implies that there exists a positive constant c₄ which depends on the constants c₀,c₁,c₂,m_A,m_K,S,m^∗,and p^∗ of the problem such that Thus,the sequence (x_zn ) is bounded in the Hilbert space X. There exists ∈ X and a subsequence (x_znk) such that 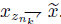. Since U ⊂ X is a closed convex subset,it is weakly closed and 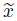∈ U. Moreover,using the compactness of the trace map γ : X → L₂(Γ_C)d × L²(Γ_C),it follows from the weak convergence of (x_znk) that Next,let us prove that 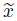is the solution of (50). We have

From (34),(38),and (z_n) ¬ z,we get and from

we get The two previous results (69) and (70) give Furthermore,the inequality

gives

It follows from (62) that

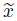Now,we combine (62),(71),and (72) with the pseudo-monotonicity of A to deduce Thus,we find that is a solution of Problem (PV_z),and from the uniqueness of the solution for this variational inequality,we deduce that 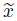= x_z. Moreover,since x_z is the unique weak limit of any subsequence of (x_zn),we obtain that the whole sequence (x_zn) is weakly convergent in X to x_z. Consequently,the mapping z → x_z is weakly continuous.

We end this proof with the remark that the mappings z → x_z and z → θ_z are weakly continuous implying that the mapping z → 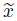_z is weakly continuous.

Lemma 4.5 For specified values of k₁ and k₂,the operator ∧ has at least one fixed point.

Proof Let us consider z = (z₁,z₂) ∈ K₁ × K₂,i.e.,

Then,

Since z₁ = ψ(u_zυ −g) φ_L(φ_z −φ_F) and z₂ = k_c(u_zυ −g) φ_L(θ_z −θ_F),it follows from the bounds |ψ(u_zυ − g)| ≤ M ,|kc(u_zυ − g)| ≤ M_kc ,and |φ_L(ζ_z − ζ_F)| ≤ L that and From the definition of the operator ∧,we have

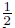Hence,if we select k₁ = M_ψLmeas(ΓC) and k₂ = M_kc L meas(ΓC) 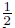,we obtain

Thus,∧ is an operator from the non-empty,convex,and closed subset K₁ × K₂ of L²(Γ_C)² into itself. Since the space L²(Γ_C)² is reflexive,K₁ × K₂ is weakly compact. The assumptions (h₃)-(h₄) and the continuity of the operators φ_L and k_c,combined with Lemma 4.4,lead to the weak continuity of ∧. Hence,by Schauder’s fixed point theorem,the operator ∧ has at least one fixed point.

Now,we have all the ingredients to provide the proof of Theorem 3.1.

(i) Let z^∗ be the fixed point of the operator ∧ and denote by x^∗ = (u^∗,φ^∗,θ^∗) the solution of the variational problem (PV_z) for z = z^∗. The definition of ∧ and Problem (PVz) proves hat x^∗ is a solution of Problem (PV),which leads to the existence part of Theorem 3.1.

(ii) We introduce the operators A : X → X and B : X → X defined by

where A is given by (47). We also introduce the functions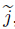 ,,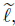and 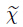on X and the element 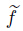∈ X by the following equalities:

Using (76),(77),(78),(79),(80),(81),and (56),it is easy to see that 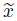= (u,φ,θ) is a solution of Problem (PV) if and only if

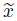Now,let ₁ = (u₁,φ₁,θ₁) and 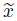₂ = (u₂,φ₂,θ₂) be the solutions of (82). Then,

Take = ₂ in the first inequality, = ₁ in the second one,and add the two inequalities to get such that

By (79) and (80),we have

and

Using the proprieties of φ_L,ψ,and k_c,we deduce Moreover,it follows from (77) and (h₂) that

Using (56),we find Using the properties of truncation operators A and K,it is easy to see that the operator A is a strongly monotone Lipschitz continuous operator on X.

Finally,we combine (83) and (84)-(85) to prove that there exists a constant c^∗ > 0 such that

Let L^∗ = . If

then we obtain ₁ = ₂,which ensures the uniqueness.