Shanghai University
Article Information
- Yanmei YUE, Xiaofen YE, Kaiyu XU. 2015.
- Analytical solutions for plane problem of functionally graded magnetoelectric cantilever beam
- Appl. Math. Mech. -Engl. Ed., 36(7): 955-970
- http://dx.doi.org/10.1007/s10483-015-1980-9
Article History
- Received 2014-10-24;
- in final form 2015-03-11
The development of magnetic and electronic material has been penetrated in every fieldof modern technology. Owing to the trend of device miniaturization,multifunctional materi-als with the properties of electricity and magnetism have attracted more and more interests.Magnetoelectric (ME) structures have the magneto-electro-elastic coupling property,with theability to convert energy from one form (among magnetic,electric,and mechanical energies)to another. Many references[1, 2, 3, 4, 5] show us the recent research of ME materials. Because ofthe coupling effects,ME materials have significant application prospects in sensor technology,memory devices,and smart structures[6, 7, 8, 9].
For ME materials,the ME effect is one of the most important research topics. Recently,it is confirmed that the ME effect can be enhanced in the functionally graded multiferroicmaterials[10, 11]. The functionally graded material (FGM) is a kind of material with mate-rial composition and properties varying continuously along certain directions. The intelligentdevices made of FGMs have no discernible internal boundaries and do not produce stress con-centration while they are loaded. The concept of FGMs was first proposed in 1984 by mate-rial scientists as a means of preparing thermal barrier materials[12]. Since then,FGMs havebeen applied to various fields such as electronic,chemical,optical,acoustic,and biomedicaltechnologies[13, 14, 15, 16]. For practical problems in multifunctional materials,the direct solution[17]and various effective numerical methods (such as the finite element method[18] and the bound-ary element method[19, 20]) are generally adopted to study the transformation between force,electricity,and magnetism. However,in order to verify the correctness of numerical calculationmethod and check the precision of numerical results,it is still necessary and meaningful to seekanalytical solutions.
Shi[21] and Shi and Chen[22] studied the response of functionally graded piezoelectric beamsand presented the analytical solutions. However,in their analysis,only one or two materialparameters were assumed to vary in the form of finite power series along the thickness directionwith other parameters being kept constant. Zhong and Yu[23] provided the analytical solutionfor the problem of a cantilever functionally graded elastic beam subjected to different loadsby assuming that all the elastic moduli of the material have the same variations along thebeam-thickness direction. Pan and Han[24] presented an exact solution for functionally gradedlayered magneto-electro-elastic plates with all material constants varying in the same expo-nential way along the thickness direction by the pseudo-Stroh formalism and the propagatormatrix method. Ding et al.[25] obtained elasticity solutions for plane anisotropic functionallygraded beams by considering the elastic compliance parameters being arbitrary functions of thethickness coordinate. Huang et al.[26] investigated the bending problem of anisotropic function-ally graded magneto-electro-elastic (FGMEE) plane beams subjected to polynomial loads ontheir upper/lower surface with various boundary conditions being applied at the two ends ofthe beams. Li et al.[27] presented a three-dimensional analytical solution for FGMEE circularplates subjected to a uniform load. By introducing stress,electric displacement,and magneticinduction functions,Huang et al.[28] obtained an analytical solution and a semi-analytical solu-tion for the anisotropic FGMEE beam subjected to distributed sinusoidal loadings. However,their analytical solution is only suitable for FGMEE beams with exponential variation or powerfunction variation along the thickness. To the authors’ knowledge,no general solution has beenfound to be adaptive to arbitrary material property variation for FGMEE beams until now.
In this paper,we present a general solution of a cantilever FGMEE with arbitrary gradedvariations of material property distribution based on the two-dimensional theory of multiferroicmaterial. In Section 2,the basic equations and boundary conditions are described. In Section 3,the stress,the electric displacement,and the magnetic induction are expressed,respectively,ina particular form involving certain unknown functions of the thickness coordinate. Then,an an-alytical solution of a plane problem is formulated. In Section 4,the numerical results and dis-cussion are given for specific examples. Finally,some conclusions are summarized in Section 5. 2 Basic equations
As shown in Fig. 1,a magneto-electro-elastic cantilever with a rectangular cross-section ofthe height h and the width b is subjected to a uniform load q on the upper surface and aconcentrated force P and moment M at the end of the beam. When the width b is muchsmaller than the height and the length,this problem can be treated as a plane stress problem.
 |
| Fig. 1 Geometric model of magneto-electro-elastic cantilever beam |
The constitutive equations for this plane stress problem can be written as
where σx,σz,and τzx denote the stress components,"x,"z,and zx are the strain components,and Ek,Dk,Hk,and Bk (k = x,y) are,respectively,the components of electric field,electricdisplacement,magnetic field,and magnetic flux. sij ,dij ,qij ,λij ,μij ,and μij denote thecoefficients of elastic compliance,piezoelectricity,piezomagnetism,dielectric impermeability,magnetic permeability,and magneto-electricity,respectively.Assume an FGM with the function variation in the z-direction. The material coefficients in Eq. (1) can be described as
where sij0 ,dij0 ,qij0 ,μij0 ,μij0 ,and αij0 are the material coefficients for z = z0 and F (z0) = 1.The equilibrium equations without the body force and the electric charge can be written as
The geometrical equations are
The equation of strain compatibility for the plane stress problem is expressed as
For the cantilever beam,the boundary conditions are given as follows:(i) The boundary conditions for the external force are
At x = 0 and z =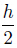 While at x = 0 and z = −
While at x = 0 and z = −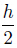
(ii) The boundary conditions for electric and magnetic fields are
at the ends of the beam (i.e.,x = 0 and x = l),and at the upper surface and under the surface (i.e.,z = ±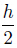 ).
).
(iii) The displacement boundary conditions at the clamped end (z = 0 and x = l) are
3 Stress,electric displacement,and magnetic induction functions and analyticalsolution of FGMEE plane problemFirstly,we introduce the Airy stress function U(x,z) which satisfies the following equations:
Substituting Eqs. (5),(6),and (14) into Eq. (1) and based on the compatibility equation (7) and the last two equations of equilibrium equations (3),we obtain
Then,we assume By substituting the assumptions into Eq. (15),we can get the following relations: where

Firstly,we introduce some new symbols


Since the expressions of f(z) and f1 (z) ,f2(z),· · · ,f8(z) are obtained,the Airy stress func-tion U(x,z),the electric potential φ,and the magnetic potential all can be determined. Therefore,the stress,electric field,and the magnetic field can be expressed asφ
Substituting Eqs. (20)-(26) into Eq. (1),we can obtain the expressions of the strains,the electric displacements,and the magnetic fluxes as follows:
where

Similarly,the displacement in the z-direction can be obtained by integrating Eq. (28) withrespect to z as follows:
Notice that there are two unknown functions g1(z) and g2 (x) in the expressions of displace-ments u and w. Using the shear strain-displacement relations in Eqs. (4),(31),(34),and (35),the forms of g1(z) and g2 (x) are expressed as
The determinations of all the unknown coefficients included in Eqs. (20)-(37) are given in Appendix A. 4 Examples and discussion
In the following numerical example,the dimensions ofME cantilever beam shown in Fig. 1 areset as l = 0.3m,h = 0.02m,and b = 0.02m. The loads are as follows: q = 1N/m2,P = 10N,and M = 1N·m. Two kinds of gradient function of material parameters are considered: theexponential function F(z) = ek  (k = 0,1,2) and the linear function F(z) = 1 + k
(k = 0,1,2) and the linear function F(z) = 1 + k  (k = 0,1,1.9),where k is the gradient factor characterizing the degree of the material gradient inthe z-direction. It is obvious that k = 0 corresponds to the homogeneous material case. Thephysical parameters of the magneto-electro-elastic material at z = 0 are recorded in Table 1.
(k = 0,1,1.9),where k is the gradient factor characterizing the degree of the material gradient inthe z-direction. It is obvious that k = 0 corresponds to the homogeneous material case. Thephysical parameters of the magneto-electro-elastic material at z = 0 are recorded in Table 1.
In Table 1,the units are the elastic stiffness sij ,10−12 m2/N,the piezoelectric constant dij ,10−13 C/(N·m),the piezomagnetic constant qij ,10−9 N/(A·m),the dielectric constant λij ,10−8 F/m,the magnetic permeability mij ,10−6 N·s2/C2,and the electromagnetic contant αij ,10−8 N·s/(V·C).
Figures 2 and 3 show the z-dependent variation of all physical quantities (stresses,electricdisplacements,magnetic fluxes,and displacements in the x- and z-directions) at the locationof x = l/6. In all the figures,we compare five kinds of ME materials: (i) the homogeneousmaterial (i.e.,k = 0); (ii) the exponential gradient function with k = 1; (iii) the linear gradientfunction with k = 1; (iv) the exponential gradient function with k = 2; (v) the linear gradientfunction with k = 1.9.
 |
| Fig. 2 Variation of physical quantities along z-direction for FGMEE beam at cross section x = l/6 |
Observing Figs. 2(a)−2(g),it can be seen that when k = 1,the curves of physical quantities of material parameters withexponential variation and linear variation are essentially coincident,which indicates that the two kinds of gradient function have the same effect.
Figure 2(a) shows the z-dependent variation of σx. It gives the information that for theFGM,the stress σx is a nonlinear distribution with respect to z,and the location of centralaxis is upward with the increase of gradient factor k. In particular,the absolute value of thestress σx on the upper surface of the beam is larger than that on the lower surface. For the caseof homogeneous material,σx changes linearly with respect to z and is also antisymmetric withrespect to the central axis. These coincide with the results of classical solution of elasticity.
Figure 2(b) shows the z-dependent variation of stress σz. It is a nonlinear distribution andincreasing along the z-direction. For the material with the same gradient distribution,theabsolute value of σz decreases with the increase of k.
Figure 2(c) gives the distribution of shear stress τzx along the z-direction. It is obvious thatthe distribution of τzx is parabolic. For the homogeneous material (i.e.,k = 0),τzx takes themaximum value in the neutral axis which is also consistent with the classical solution. However,for the FGM,although τzx also has the maximum value in the neutral axis,it is no longer asymmetric distribution on the cross section. It is noteworthy that the maximum absolute valueof τzx on the cross section increases with k when the beam is subjected to the same externalforce and has the same type of gradient distribution.
Figure 2(d) shows that the electric displacement Dx is also a parabolic distribution alongthe z-direction. For the homogeneous material,the electric displacement has a symmetricdistribution with respect to z = 0. The values of Dx on the lower and upper surfaces are equalto each other,and they are all nonzero. It indicates that the beam achieves electro-mechanicalconversion under the effect of external forces. For the FGM,Dx on the lower surface is larger than that on the upper surface. At the same time,the differential of electric displacement on the upper and lower surfaces enlarges when k increases.
Figure 2(e) shows that Dz has a nonlinear distribution with respect to z,and it reaches thepeak value at the location of h/4 and 3h/4,respectively. For a given gradient distribution,thelarger the gradient factor k is,the more Dz increases.
The distributions of magnetic fluxes Bx and Bz in Figs. 2(f) and 2(g) have the similar trendsas those of Dx and Dz. Regardless of the gradient variation and the value of k,Bx (or Bz) is twomagnitudes larger than Dx (or Dz). This phenomenon tells us that the magneto-mechanicalconversion is more remarkable than the electro-mechanical conversion.
Figures 3(a)-3(b) show the x-dependency of displacements u and w at the section centroid.Figure 3(a) expresses that with the increase of k in the gradient function,the displacement uincreases. However,in Fig. 3(b),for the FGM with exponential variation,the deflection w isnot affected by the gradient factor k. For the FGM with linear variation,w decreases with theincrease of k.
 |
| Fig. 3 Displacements of FGMEE beam at section centroid (z =0) |
We derive an analytic solution of the two-dimensional plane problem for a functionallygraded ME cantilever beam by the semi-inverse method. This solution can be used to solvethe problems of the beam with any gradient distribution under different boundary conditions(such as the uniform load on the surface,the concentrated force,and the moment at the freeend of the beam). This solution can also be used as a validation of numerical solutions of thefunctionally graded ME composite. Our main conclusions are as follows:
(i) If the gradient factor k is 1,the exponential and linear gradients have the same effect onall the physical quantities.
(ii) The central axis moves up with the increase of the gradient factor k. The shear stressreaches its maximum at the central axis,and its absolute value increases with the increase ofk.
(iii) The components of electric displacement and magnetic flux in the same direction havethe similar distribution,but the value of the magnetic flux is two magnitudes larger than thatof the electric displacement.
(iv) If the gradient factor k increases,the difference of electric displacements Dx (or themagnetic flux Bx) on the upper and lower surfaces enlarges,and Dx (or Bz) increases too.
(v) No matter the material parameters are exponential or linear variation,the displacementu increases with the increase of k,while the deflection w has very different results. For the FGMwith exponential variation,the changes of gradient factor have no effect on the deflection w. For the FGM with linear variation,the deflection w decreases with the increase of the gradient factor k. Appendix A
The expressions of undetermined coefficients contained in Eqs. (20)-(37) are given as follows. By virtue of Eq. (9),Eq. (10),and the first expression of Eq. (8),we can obtain


Using the boundary conditions (11) and (12),we can determine the following parameters:


By the force boundary conditions in Eq. (8),C13 and C14 can be determined.




| [1] | Liu, L. P. An energy formulation of continuum magneto-electro-elasticity with applications. Journal of the Mechanics and Physics of Solids, 28, 560-568 (2009) |
| [2] | Luo, X. B., Wu, D., and Zhang, N. Room temperature magneto-birefringence in composites of stress-birefringence and magnetostriction. Journal of Applied Physics, 113, 173903 (2013) |
| [3] | Zhong, X. C. and Lee, K. Y. Dielectric crack problem for a magnetoelectroelastic strip with functionally graded properties. Archive of Applied Mechanics, 82, 791-807 (2012) |
| [4] | Hadjiloizi, D. A., Georgiades, A. V., Kalamkarov, A. L., and Jothi, S. Micromechanical modeling of piezo-magneto-thermo-elastic composite structures: part I—theory. European Journal of Mechanics-A/Solids, 39, 298-312 (2013) |
| [5] | Fang, F., Shan, S. C., and Yang, W. Magnetoelectric coupling of Terfenol-D/P (VDF-TrFe) /Terfenol-D laminates mediated by crystallite size of electroactive polymer. Acta Mechanics, 224, 1169-1174 (2013) |
| [6] | Dong, S. X., Li, J. F., and Viehland, D. Vortex magnetic field sensor based on ring-type magnetoelectric laminate. Applied Physics Letters, 85, 2307-2309 (2004) |
| [7] | Spaldin, N. A. and Fiebig, M. The renaissance of magnetoelectric multiferroics. Science, 309, 391-392 (2005) |
| [8] | Eerenstein, W., Mathur, N. D., and Scott, F. Multiferroic and magnetoelectric materials. nature, 442, 759-765 (2006) |
| [9] | Srinivasan, G., Zavislyak, I. V., and Tatarenko, A. S. Millimeter-wave magnetoelectric effects in bilayers of barium hexaferrite and lead zirconate titanate. Applied Physics Letters, 89, 152508 (2006) |
| [10] | Wang, X., Pan, E., Albrecht, J. D., and Feng, W. J. Effective properties of multilayered functionally graded multiferroic composites. Composite Structures, 87, 206-214 (2009) |
| [11] | Sladek, J., Sladek, V., Krahulec, S., and Pan, E. Enhancement of the magnetoelectric conefficient in functionally graded multiferroic composites. Journal of Intelligent Material Systems and Structures, 23, 1649-1658 (2012) |
| [12] | Ichikawa, K. Functionally Graded Materials in 21st Century: a Workshop on Trends and Forecasts, Springer, New York, 18-20 (2000) |
| [13] | Hirai, T. and Chen, L. Recent and prospective development of functionally graded materials. Japanese Material Science Forum, 509, 308-311 (1999) |
| [14] | Wang, Y. S., Huang, G. Y., and Dross, D. On the mechanical modeling of functionally graded interfacial zone with a Griffith crack: anti-plane deformation. Journal of Applied Mechanics, 70, 676-680 (2003) |
| [15] | Hart, N. T., Brandon, N. P., Day, M. J., and Lapeña-Rey, N. Functionally graded composite cathodes for solid oxide fuel cells. Journal of Power Sources, 106, 42-50 (2002) |
| [16] | Pompe, W., Worch, H., Epple, M., Friness, W., Gelinsky, M., Greil, P., and Hempel, D. Functionally graded materials for biomedical applications. Material Science and Engineering A, 362, 40-60 (2003) |
| [17] | Petrov, V. M. and Srinivasan, G. Enhancement of magnetoelectric coupling in functionally graded ferroelectric and ferromagnetic bilayers. Physical Review B, 78, 184421 (2008) |
| [18] | Wang, R. F. and Pan, E. Three-dimensional modeling of functionally graded multiferroic composites. Mechanies of Advanced Material Structures, 18, 68-76 (2011) |
| [19] | Ding, H. J., Wang, G. Q., and Chen, W. Q. A boundary integral formulation and 2D fundamental solution for piezoelectric media. Computure Methods in Applied Mechanics and Engineering, 158, 65-80 (1998) |
| [20] | Ashrafi, H., Asemi, K., and Shariyat, M. A three-dimensional boundary element stress and bending analysis of transversely/longitudinally graded plates with circular cutouts under biaxial loading. European Journal of Mechanics-A/Solids, 42, 344-357 (2013) |
| [21] | Shi, Z. F. General solution of a density functionally gradient piezoelectric cantilever and its applications. Smart Material and Structures, 11, 122-129 (2002) |
| [22] | Shi, Z. F. and Chen, Y. Functionally graded piezoelectric cantilever beam under load. Archive of Applied Mechanics, 74, 237-247 (2004) |
| [23] | Zhong, Z. and Yu, T. Analytical solution of a cantilever functionally graded beam. Composites Science and Technology, 67, 481-488 (2007) |
| [24] | Pan, E. and Han, F. Exact solution for functionally graded and layered magneto-electro-elastic plates. International Journal of Engineering Science, 43, 321-339 (2005) |
| [25] | Ding, H. J., Huang, D. J., and Chen, W. Q. Elasticity solutions for plane anisotropic functionally graded beams. International Journal of Solids and Structures, 44, 176-196 (2007) |
| [26] | Huang, D. J., Ding, H. J., and Chen, W. Q. Analytical solution for functionally graded magnetoelectro- elastic plane beams. International Journal of Engineering Science, 45, 467-485 (2007) |
| [27] | Li, X. Y., Ding, H. J., and Chen, W. Q. Three-dimensional analytical solution for functionally graded magneto-electro-elastic circular plates subjected to uniform load. Composite Structures, 83, 381-390 (2008) |
| [28] | Huang, D. J., Ding, H. J., and Chen, W. Q. Static analysis of anisotropic functionally graded magneto-electro-elastic beams subjected to arbitrary loading. European Journal of Mechanics- A/Solids, 29, 356-369 (2010)" |
 2015, Vol. 36
2015, Vol. 36








































