Shanghai University
Article Information
- Xiaodong WANG, Yushu CHEN, Lei HOU. 2015.
- Nonlinear dynamic singularity analysis of two interconnected synchronous generator system with 1:3 internal resonance and parametric principal resonance
- Appl. Math. Mech. -Engl. Ed., 36(8): 985-1004
- http://dx.doi.org/10.1007/s10483-015-1965-7
Article History
- Received Dec. 23, 2014;
- in final form May 22, 2015
The stability of electric power systems is a well-established subject with a long history of research [1] . Actual power systems are forced to operate closer to their stability limits due to the increasing power demands and other factors such as environmental and economical constraints for building new power plants and transmission lines. Recently,electric power systems have become much huger and more complicated. Stability problems have become more complex as interconnections become more extensive. Therefore,the stability analysis of electric power systems is still a major issue and has been received significant attention in scientific studies.
Due to the high nonlinearity of the electric power system,its stability is closely related to a disturbance. If the disturbance is large,the system operating point varies significantly,and nonlinearities may have a considerable effect on the system performance. In this situation,the equations that describe the dynamics of the power system cannot be linearized. The tools of assessment for this type of stability belong to nonlinear system theory,which include geomet- ric methods,energy functions,bifurcation theories,normal forms of vector fields,and numerical simulations [1, 2, 3] . The stability analysis can be carried out by using nonlinear dynamic methods [4, 5] and perturbation techniques [6] ,which are widely used in nonlinear mechanics [7].
There has been great concern in the power system research field on dynamic characteris- tics relating to the stability of a power system. Some researchers focused their attention on an equivalent single-machine infinite-bus (SMIB) power system. A good example of using the perturbation method of multiple scales for stability analysis of a single machine power system was studied by Nayfeh et al. [8, 9] . Duan et al. [10] gave a bifurcation analysis for an SMIB power system with series capacitor compensation associated with sub-synchronous resonance. Chen et al. [11] showed the presence of chaos in an SMIB power system through a period-doubling bifurcation route,and they also investigated the chaotic control and chaotification problem of that system. Wang et al. [12] investigated dynamical behaviors and singularities in an SMIB power system formulation by using the geometric singular perturbation theory. Chen et al. [13] used Melnikov’s method to discuss hetero-clinic and sub-harmonic bifurcations and gave a con-dition of parameters for chaotic oscillation occurrence in an SMIB power system. Wei et al. [14] analyzed the effect of the Gaussian white noise on erosion of safe basin in the same model under different parameters.
The advantage of the SMIB representation is the simplicity of the model which facilitates sophisticated nonlinear analysis. However,such models are limited to study instability events involving many generators. For multi-machine power systems,many techniques have been de- veloped and applied to the stability analysis in terms of theoretical analysis [15, 16] ,numerical methods [17] ,and engineering applications [18, 19].
A power system is inherently a complex nonlinear system,which exhibits complex dynamic behavior when subjected to disturbances. For two or more machines infinite-bus power sys-tem,there exist coupled power angles in the motion equations (called swing equations) which describe the dynamic characteristics of the interconnected synchronous generators. It has been pointed out that the inter-area modal phenomenon may occur as a result of a nonlinear in-teraction of the natural oscillation modes of stressed power system. The conventional linear techniques [20] analyze the linear modal behavior and cannot account for many complex phe-nomena that occur when the system is stressed. Therefore,for a better understanding of the underlying cause of the complex behavior of a stressed power system,many researchers have turned to seek new methods. Many scientists have made great efforts on applying the method of normal forms to quantify nonlinear modal interaction in power systems [21, 22, 23, 24] and strong modal resonance analysis [25] ,as similar to the most widely considered ones for studying the normal mode bifurcation in nonlinear mechanical systems[26, 27, 28, 29] .
For a two-machine infinite-bus (TMIB) power system,Yuan and Sun [30] studied the occur- rence of chaotic phenomenon by using Melnikov’s method under some particular conditions. They proposed a two-generator electric power system model by considering that the infinite-bus maintains a voltage of fixed amplitude with a small periodic fluctuation in the phase angle. However,the internal resonance in the system subjected to disturbances has not been discussed.
The motivation of this paper is to investigate the internal resonance and its effect on the bi-furcation characteristics of a TMIB power system. Besides the fluctuation of changing phase [31] , the fluctuation of changing voltage is also considered to formulate the infinite-bus in our con-sidered model. The approximate solutions to normal modes of this system with or without the internal resonance are derived by using the method of multiple scales. For comparison,the bifurcation analysis for the case of no internal resonance is carried out by using the single-state-variable singularity method to show the basic bifurcation characteristics of the system. Then, the 1:3 internal resonances are proposed,and the bifurcation equations are studied successfully by employing the two-state-variable singularity method,which reveal the effects of the infinite-bus voltage amplitude and phase fluctuations on mode solution bifurcation characteristics of this system.
2 Mathematical model of TMIB power systemA simple interconnected power system model with two generators and three nodes in this paper is shown in Fig. 1,where the synchronous generators G1 and G2 are delivering power to the infinite-bus through transmission lines and main transformers XT1 ,XT2 . The number “3” represents the infinite-bus node. The motion equations of the two generators can be written as follows [30, 31] :
 |
| Fig. 1 Schematic diagram of two-machine power system |
Use an identical procedure,and let
where θ20 is the operating value of δ2around which the variation Δδ = δ2− θ20 takes place. Then,one can obtainExpanding (1) in a Taylor series around θ10,θ20,and retaining terms up to third order,we obtain the following modified swing equation:
where the corresponding coefficients are listed in Appendix A.3 Perturbation and singularity analysis
In this section,we use the method of multiple scales [7] to obtain a set of four averaged equations that determine the amplitudes and phases of the steady-state solutions on a slow scale. It is noted that this technique is applicable to the cases with or without an internal resonance. The investigation for the case of no internal resonance is first given for comparison. Then,we study the case of internal resonance. Assume that the solutions of (7) in the neighborhood of the trivial equilibrium are represented by an expansion of the form:
where ε is a small positive parameter,T0= t represents a fast scale,and T1= εt is a slow scale characterizing modulation of the amplitudes and phases of two modes. In terms of T0 and T1, the time derivatives transform according to where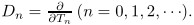
To obtain a system which is suitable for the application of the method of multiple scales, the scales transformations may be introduced as follows:
Substituting (8)-(10) into (7) and equating the coefficients of the same order of ε in both sides,one obtains the following sets of differential equations:Order ε0:
Order ε1:
From the left-hand side of (11),it can be seen that there exist coupled interaction terms of x0 and y0,and supposing that its solution has the following form: where “Cc ” stands for the complex conjugate of the preceding terms. The quantities A1and A2are unknown at this stage of the analysis,they are determined by eliminating the secular terms at the next approximation,and jω1,and jω2are two different pure imaginary roots of the following characteristic equation about λ:Supposing0< ω1< ω2,it is worth pointing out that ω1,and ω2are also called the first-order and the second-order natural frequencies of the normal modes,respectively. For the case of the parametric principal resonance,the disturbance frequency ω is assumed to be almost equal to the second-order natural frequency ω2 according to
where σ1is an external detuning parameter to express the nearness of Ω to ω2
The 1:3 internal resonances may occur under the condition that two natural frequencies of
the system satisfy such relationship ω1/ω2 = 1/3. For comparison,the bifurcation analyses
of the system for both of the non-internal resonance and the 1:3 internal resonance cases are
discussed,respectively.
3.1 Case of no internal resonance
In this case,the physical parameters are chosen such that the natural frequencies of the two modes are not of the ratio of 1:3,that is,
Substitute (13) into (12). In order to eliminate the terms that lead to secular terms from (12),suppose that its particular solution can be written as
Substituting (13) and (16) into (12) and equating the harmonic coefficients of the frequencies ω1and ω2 for both sides leads to
whereIn (17),the harmonic term whose frequency is ω1(or ω2 ) relies on both the left and the right sides to balance each other,with the following solvability condition:
The solvability condition can be written as Introducing the polar representation for A1(T1) = a1(T1)ejθ1(T1) and A2(T1) = a2(T1)ejθ2(T1) into (19) and then separating real and imaginary parts give rise to where for notation purpose,four functions a1(T1),a2(T1),θ1(T1),and θ2(T1) have been ex- pressed by a1,a2,θ1,and θ2,respectively.By letting φ= σ1T0+φV−θ2 ,the steady solution can be obtained by finding the solutions to the four algebraic equations which can be obtained by letting D1θ1= D1θ 2 = D1a1= D1a2 = 0 in (20). Then,(20) becomes
According to the typical phenomenon of a multi-degree-of-freedom vibration system [32] , when the disturbance frequency is close to the second-order natural frequency,because of the presence of damping,only the second-order mode determines the long-term dynamic behavior of the system. Therefore,we can let a1=0in (21),which yields
(22) can be transformed into the following form: where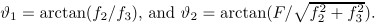
Considering the resonance condition,we can have 2ω2 ≈ 2ω,by letting
(23) can be written as Eliminating the trigonometric terms by using the relations between trigonometric functions in (24) gives rise to (25) is the so-called frequency-response equation,which can reflect the bifurcation characteris- tics of the second-order mode as the disturbance frequency ω changes. Actually,some system parameters of the TMIB power system may also change,which can lead to a sudden change in the mode amplitude. This has a significant effect on the power system’s stability and secure operation. Therefore,in order to discuss the bifurcation characteristics in a wider parameter space,the engineering unfolding analysis is carried out [33] . Let z = a22 . Then,(25) becomes where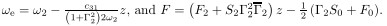
Choose ω as a bifurcation parameter and VB1and δB1as unfolding parameters. The tran-sition sets can be obtained by using the singularity theory with one variable as follows [34] :
where For a given TMIB power system,the values for the system parameters are [1] listed as follows: ω0= 100π,VB0= 1,H1= 2.37,Pm1= 1,V1= 1.27,H2= 2.37,Pm2= 1,V2= 1.27,B12= 0.1,B13= 1.2,B23= 1.0,ω = 8.1,D1= 0.008,D2= 0.008. Figure 2shows the transition sets in VB1-δB1symmetrical plane which is divided into four regions. The frequency-response curves in four regions are shown in Figs.3,4,5,6,respectively. It can be seen that every bifurcation dia-gram corresponding to different region possesses different topological structures. It should be noted that all of the frequency-response curves present softening nonlinearity and the jump phe-nomenon can occur at a lower frequency. As shown in Fig. 6(a),when the disturbance ratios of the infinite-bus voltage amplitude and phase angle are both less than 5%,the frequency-response curve in Region IV is nearly close to be a single-valued curve with small amplitude,and the jump and hysteresis phenomena do not appear. The frequency-response curves depicted in Fig. 6(b) also lie in Region IV,but in this case,the disturbance ratios of the infinite-bus voltage amplitude and phase angle are 5% and 25%,respectively. We can see that the jump and hys-teresis phenomena occur. Therefore,for an actual TMIB power system,it is better to choose the physical parameters lying in Region IV and guarantee the disturbance ratios of the infinite-bus voltage amplitude and phase angle are both less than 5%. For these chosen parameters,the generator rotors swing periodically with small amplitude,which can avoid losing synchronism. |
| Fig. 2 Transition sets with four regions |
 |
| Fig. 3 Bifurcation diagram in Region I |
 |
| Fig. 4 Bifurcation diagram in Region II |
 |
| Fig. 5 Bifurcation diagram in Region III |
 |
| Fig. 6Bifurcation diagram in Region IV (small disturbance) and bifurcation diagram in Region IV (big disturbance) |
When there exists a relationship ω2 ≈ 3ω1,the case of 1:3 internal resonance will occur. Introduce a detuning parameter σ2to express the nearness of the two natural frequencies
Suppose the solution of (11) has the following form: Substituting (28) into (12) and taking into consideration (17),we can obtain where ψ1= ω1T0+ β1(T1),ψ2= ω2 T0+ β2(T1),and θ = ωT0+ φθ.According to the solvability condition expressed by (19) and separating the same harmonic term leading to secular terms yields the governing equations for the amplitudes a1,a2and phases γ1,γ2as follows:
where γ1=3β1−σ2T1−β2,γ2=3β1−σ2T1−σ1T1−φV,and γ 3 = γ2−γ1,and the corresponding symbols are listed in Appendix B.The steady-state solutions correspond to a1,a2=0and ý1,ý2= 0. Eliminating the trigono-metric terms in (29) gives rise to
When 1:3 internal resonances take place,the singularity theory with single variable is not applicable for bifurcation characteristic analysis of (30) which has two mode amplitudes. Here, for two-machine power system,we first use the singularity method with two variables to discuss the bifurcation behaviors of the two normal mode solutions. In(30),letting x=a21 ,y=a22 as two state variables,supposing λ = σ1is the bifurcation parameter,VB1,and δB1are engineer-ing unfolding parameters. According to the singularity method with two variables [35−36] ,the transition sets are obtained by the following formulae (the corresponding symbols are listed in Appendix C):Consider a specific system with the system parameters: Rated MVA=160,Rated PF=0.85, Rated KV=15,ω0= 100π,H1= 2.37,Pm1= 1.0,B13= 1.2,B12= 1.0,V1= 1.0,H2= 0.6,Pm2= 0.6 B23 = 1,V2= 1.0,VB0= 1.0,D1= 0.008,and D2= 0.005. Fig. 7 shows the transition sets in VB1-δB1plane which is divided into seven regions. The frequency-response curves of the two modes in every region are shown in Fig. 8. As the infinite-bus voltage ampli-tude and phase fluctuate periodically,the frequency-response curves of the two modes exhibit parametric vibration characteristics as shown in Fig. 8. Owing to occurrence of 1:3 internal resonances,the first-order mode amplitude is considerably larger than that of the second-order mode. We can see that when the infinite-bus voltage amplitude or phase fluctuates,both of the two mode solutions exhibit rich bifurcation patterns leading to a change in the number of the possible normal mode solutions,for example,three to two,three to one,or two to three.
 |
| Fig. 7 Transition sets with seven regions |
 |
| Fig. 8 (a)Bifurcation diagrams in Region I; (b)bifurcation diagrams in Region II; (c)bifurcation diagrams in Region III; (d)bifurcation diagrams in Region IV; (e)bifurcation diagrams in Region V; (f)bifurcation diagrams in Region VI; (g)bifurcation diagrams in Region VII |
In comparison with no internal resonance,it can be found that the bifurcation behavior and stability of the system are significantly influenced by the infinite-bus voltage amplitude and phase. The coupled modes of the TMIB power system have more critical bifurcation points and quite rich bifurcation patterns,which is greatly different from that of no internal resonance case.
Such work is obviously preliminary to a closer understanding of the complex bifurcation behavior of the TMIB power system. When making parameter design for the system stability, it is better to avoid choosing these parameters corresponding to the critical points,where the state of motion may change suddenly. We can adjust the system parameters to achieve a required working pattern in practical engineering applications. Therefore,the above discussion can provide a theoretical direction for the dynamic analysis,bifurcation control,and engineering optimization design for an actual TMIB power system with different working and structural parameters.
4 ConclusionsIn this paper,the bifurcation analysis of a simple electric power system involving two syn-chronous generators connected by a transmission network to an infinite-bus has been carried out. In this system,the infinite-bus voltage are considered to maintain two fluctuations in the amplitude and phase angle. By using the method of multiple scales,the bifurcation equations of this system have been obtained. Then,the singularity methods for single state variable and for two state variables have been respectively used to analyze the bifurcation characteristics of the system without and with 1:3 internal resonance. The transition sets determining different bifurcation patterns of the system are obtained and analyzed,which reveal the effects of the infinite-bus voltage amplitude and phase fluctuations on bifurcation patterns of this system. The results show that the bifurcation behavior and stability of the system are significantly influenced by the infinite-bus voltage amplitude and phase. In comparison with the non in- ternal resonance case,the 1:3 internal resonance makes the bifurcation characteristics more complicated and induces more numbers of bifurcation patterns. Owing to occurrence of 1:3 in- ternal resonance,the energy transfer makes that the first-order mode amplitude is considerably larger than that of the second-order mode. The results obtained in this paper will contribute to a better understanding of the complex nonlinear dynamic behaviors in a TMIB power system.
| [1] | Anderson, P. M. and Fouad, A. A. Power System Control and Stability, Wiley-IEEE Press, New York (2002) |
| [2] | Chiang, H. D. Direct Methods for Stability Analysis of Electric Power Systems:Theoretical Foundation, BCU Methodologies, and Applications, John Wiley, New York (2011) |
| [3] | Zhang, J., Wen, J. Y., and Cheng, S. J. Power system nonlinearity modal interaction by the normal forms of vector fields. Journal of Electrical Engineering & Technology, 3(1), 8-13(2008) |
| [4] | Guckenheimer, J. and Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations Vector Fields, Springer-Verlag, New York (1983) |
| [5] | Moon, F. C. Chaos Vibrations, an Introduction for Applied Scientists and Engineers, Wiley-InterScience, New York (1987) |
| [6] | Nayfeh, A. H. Introduction to Perturbation Techniques, Wiley-Interscience, New York (1981) |
| [7] | Nayfeh, A. H. and Mook, D. T. Nonlinear Oscillations, Wiley-InterScience, New York (1979) |
| [8] | Nayfeh, M. A., Hamdan, A. M. A., and Nayfeh, A. H. Chaos and instability in a power system:subharmonic-resonant case. Nonlinear Dynamics, 2, 53-72(1991) |
| [9] | Nayfeh, M. A., Hamdan, A. M. A., and Nayfeh, A. H. Chaos and instability in a power system:primary resonant case. Nonlinear Dynamics, 1, 313-339(1990) |
| [10] | Duan, X. Z., Wen, J. Y., and Cheng, S. J. Bifurcation analysis for an SMIB power system with series capacitor compensation associated with sub-synchronous resonance. Science in China Series E-Technological Sciences, 52(2), 436-441(2009) |
| [11] | Chen, H. K., Lin, T. N., and Chen, J. H. Dynamic analysis, controlling chaos and chaotification of an SMIB power system. Chaos Solitons & Fractals, 24, 1307-1315(2005) |
| [12] | Wang, J. L., Mei, S. W., Lu, Q., and Teo, K. L. Dynamical behavior and singularities of a singlemachine infinite-bus power system. Acta Mathematicae Applicatae Sinica (English Series), 20(3), 457-476(2004) |
| [13] | Chen, X. W., Zhang, W. N., and Zhang, W. D. Chaotic and sub-harmonic oscillations of a nonlinear power system. IEEE Transactions on Circuits and Systems-Ⅱ, 52(12), 811-815(2005) |
| [14] | Wei, D. Q., Zhang, B., Qiu, D. Y., and Luo, X. S. Effect of noise on erosion of safe basin in power system. Nonlinear Dynamics, 61, 477-482(2010) |
| [15] | Zhang, J., Wen, J. Y., and Cheng, S. J. Power system nonlinearity modal interaction by the normal forms of vector fields. Journal of Electrical Engineering & Technology, 3(1), 8-13(2008) |
| [16] | Revel, G., Leon, A. E., Alonso, D. M., and Moiola, J. L. Bifurcation analysis on a multimachine power system model. IEEE Transcations on Circuits and Systems-I:Regular Papers, 57(4), 937-949(2010) |
| [17] | Jiang, N. Q. and Chiang, H. D. Damping torques of multi-machine power systems during transient behaviors. IEEE Transactions on Power Systems, 29(3), 1186-1193(2014) |
| [18] | Amano, H., Kumano T., Inoue, T., and Taniguchi, H. Proposal of nonlinear stability indices of power swing oscillation in a multi-machine power system. Electrical Enginerring in Japan, 151(4), 215-221(2005) |
| [19] | Senjyu, T., Morishima, Y., Arakaki, T., and Uezato, K. Improvement of multi-machine power system stability using sdaptive PSS. Electric Power Components and Systems, 30, 361-375(2002) |
| [20] | Yu, Y. P., Min, Y., and Chen, L. Analysis of forced power oscillation steady-state response properties in multi-machine power systems (in Chinese). Automation of Electric Power Systems, 33(22), 5-9(2009) |
| [21] | Lin, C. M., Vittal, V., Kliemann, W., and Fouad, A. A. Investigation of modal interaction and its effects on control performance in stressed power systems using normal forms of vector fields. IEEE Transactions on Power Systems, 11(2), 781-787(1996) |
| [22] | Saha, S., Fouad, A. A., Kliemann, W. H., and Vittal, V. Stability boundary approximation of a power system using the real normal form of vector fields. IEEE Transactions on Power Systems, 12(2), 797-802(1997) |
| [23] | Thapar, J., Vittal, V., Kliemann, W., and Fouad, A. A. Application of normal form of vector fields to predict inter-area separation in power systems. IEEE Transactions on Power Systems, 12(2), 844-850(1997) |
| [24] | Deng, J. X. and Zhao, L. L. Study on the second order non-linear interaction of the critical inertial modes (in Chinese). Proceeding of the CSEE, 25(7), 75-80(2005) |
| [25] | Dobson, I., Zhang, J. F., Greene, S., Engdahl, H., and Sauer, P. W. Is strong modal resonance a precursor to power system oscillation. IEEE Transactions on Circuits and Systems-I:Fundamental Theory and Applications, 48(3), 340-349(2001) |
| [26] | Li, X. Y., Chen, Y. S., and Wu, Z. Q. Singular analysis of bifurcation of nonlinear normal modes for a class of systems with dual internal resonances. Applied Mathematics and Mechanics (English Edition), 23(10), 1122-1133(2002) DOI 10.1007/BF02437660 |
| [27] | Li, X. Y., Ji, J. C., and Hansen, C. H. Non-linear normal modes and their bifurcation of a two DOF system with quadratic and cubic non-linearity. International Journal of Non-Linear Mechanics, 41, 1028-1038(2006) |
| [28] | Li, X. Y., Chen, Y. S., and Wu, Z. Q. Non-linear normal modes and their bifurcation of a class of systems with three double of pure imaginary roots and dual internal resonances. International Journal of Non-Linear Mechanics, 39, 189-199(2004) |
| [29] | Nayfeh, A. H., Lacarbonara, W., and Chin, C. Nonlinear normal modes of buckled beams:three-to-one and one-to-one internal resonance. Nonlinear Dynamics, 18, 253-273(1999) |
| [30] | Yuan, B. and Sun, Q. H. Chaos in the multi-machine power system (in Chinese). Automation of Electric Power System, 19(2), 26-31(1995) |
| [31] | Ueda, Y. and Ueda, Y. Nonlinear resonance in basin portraits of two coupled swings under periodic forcing. International Journal of Bifurcation and Chaos, 8(6), 1183-1197(1998) |
| [32] | Chen, Y. S. Nonlinear Vibration (in Chinese), Higher Education Press, Beijing (2002) |
| [33] | Chen, Y. S. and Leung, A. Y. T. Bifurcation and Chaos in Engineering, Springer-Verlag, London (1998) |
| [34] | Golubitsky, M. and Schaeffer, D. G. Singluarities and Groups in Bifurcation Theory-I, Springer-Verlag, New York (1984) |
| [35] | Qin, Z. H., Chen, Y. S., and Li, J. Singularity analysis of a two-dimensional elastic cable with 1:1 internal resonance. Applied Mathematics and Mechanics (English Edition), 31(2), 143-150(2010) DOI 10.1007/s10483-010-0202-z |
| [36] | Qin, Z. H. and Chen, Y. S. Singular analysis of bifurcation systems with two parameters. Acta Mechanica Sinica, 26(3) 501-507(2010) |
 2015, Vol. 36
2015, Vol. 36








































