Shanghai University
Article Information
- Ruirui LIU, Haibo WANG, Jialing YANG, Hua LIU, Yuxin SUN. 2015.
- Theoretical analysis on quasi-static lateral compression of elliptical tube between two rigid plates
- Appl. Math. Mech. -Engl. Ed., 36(8): 1005-1016
- http://dx.doi.org/10.1007/s10483-015-1962-7
Article History
- Received Sept. 5, 2014;
- in final form May 13, 2015
2. Jiuquan Satellite Launch Center, Jiuquan 732750, Gansu Province, China
There has been a considerable interest in the behavior of energy absorption components under impact in recent years,especially with the rapid development of various transport vehi- cles such as aircrafts and automobiles in nowadays. Researchers have studied various energy absorption components for efficiently dissipating the impact energy transmitted to the people or structures being protected. The preferred energy absorbers generally exhibit the following characteristics [1] ,for instance,irreversible energy transformation,limited reactive force,stable deformation mode,long collapse stroke,low cost,and easy installation. The circular rings or short circular tubes,as the most widely applied energy absorption elements,have been ex- tensively investigated by many researchers. For example,DeRuntz and Hodge [2] ,Burton and Craig [3] ,respectively,proposed a four-hinge mechanism and a six-hinge mechanism to study the quasi-static lateral compression of a circular tube between two parallel rigid plates. Due to the absence of strain hardening effect,the predicted force-deformation response is under-estimated in comparison with the corresponding experimental results. Later,Redwood [4] employed a rigid linear strain hardening material model to account for the effect of strain hardening,and the obtained force-deformation response was improved but still under-estimated. Further,Reid and Reddy [5] proposed a hinge line theory,wherein the localized hinges were replaced by an arc whose length could change during a compression,which were in good agreement with the experimental results.
Compared with circular tubes,elliptical tubes have particular characteristics as energy ab- sorbers on account of their different semi-axes. Wu and Carney [6, 7] investigated the initial collapse behavior of braced elliptical tubes by the equivalent structure technique and experi- ments. They verified that elliptical tubes possessed longer collapse stroke and larger energy dissipation potential per unit mass when loaded along their major axes,in comparison with their circular counterparts. Olabi and coauthors [8, 9, 10, 11]] analyzed the lateral crushing of nested circular and elliptical tubes with various constraints both experimentally and numerically. They also revealed that the elliptical tubes exhibited greater crush efficiency than the circular ones.
By reviewing the existing literatures,however,no attempt has been made to investigate the unbraced elliptical tube under quasi-static lateral compression theoretically. In this paper,we will try to develop an analytical model to study the crushing behavior and energy absorption capability of a single elliptical tube,with and without considering the effect of strain hardening. The characteristics of the force-deflection curves of the elliptical tube under quasi-static lateral compression will be explained from a more general point of view.
2 Theoretical model for elliptical tubes without considering strain hard-ening effectConsider an elliptical tube under lateral compression by two parallel rigid plates,with an initial vertical semi-axis b,horizontal semi-axis a,and thickness t,as shown in Fig. 1(a). In the present model,the following assumptions are made: (i) A rigid-perfectly plastic idealization of the material is considered here. (ii) The elliptical tube is inextensible. (iii) The ovality,h = b/a, is below a certain value to prevent the global Euler buckling. Therefore,similar to the circular tube,there are four plastic rings needed to form a collapse mechanism for an elliptical tube under lateral compression,as shown in Fig. 1(b). The plastic deformation appears at the plastic hinges H and C,while the arc HC always remains rigid during the compression process.
 |
| Fig. 1 Collapse mechanism of elliptical tube compressed by two parallel rigid plates |
The free body diagram of a quarter of the elliptical tube is shown in Fig. 2. Rotating the original Cartesian coordinate system x − y counterclockwise around the origin by an angle θ, one can obtain the elliptical equation in terms of the new Cartesian coordinate system x0−y0 as follows:
The rotation matrix relating the two coordinate systems is Then, The equation for the rotated elliptical tube in terms of the original Cartesian coordinate system is By using the definition h= b/a,(4) can be rewritten as Due to the fact that y>0 in Fig. 2,the solution to (5) is |
| Fig. 2 Forces applied on quarter of elliptical tube without strain hardening effect |
From the force analysis of the quarter of the elliptical tube,we have
where P denotes the lateral load applied on the tube and L is the arm of force,i.e. The fully plastic bending moment is M0 = σ0t2l/4,where l and σ0 are the sectional breadth and material yield stress of the elliptical tube,respectively. The initial collapse load P0 can be expressed as Then,the non-dimensional load λ= P/P0 should be and the non-dimensional displacement is As the vertical coordinate of the top hinge C becomes zero,the four-hinge mechanism in Fig. 2 will disappear. At that instant,bcosθ −asinθ=0. Therefore,the maximum angle of rotation is given by 3 Theoretical model for elliptical tube with considering strain hardening effectAn elastic linear hardening material model for the elliptical tube is adopted,as illustrated in Fig. 3,where E is the initial elastic modulus,and EP the linear hardening modulus. When considering the effect of strain hardening,the localized plastic hinge H in Fig. 2 is replaced by an arc HB whose length is changeable during the compression process,as shown in Fig. 4. The magnification of arc HB in Fig. 4(a) is shown in Fig. 4(b). The end C is a localized hinge. The plastic moments at the hinges B and H are M0 and MH,respectively.
 |
| Fig. 3 Elastic linear hardening material model for the elliptical tube |
 |
| Fig. 4 Forces applied on quarter of elliptical tube with strain hardening effect |
Similar to the analysis of a circular arc [12] ,the differential equation for the deflection of arc HB in Fig. 4(b) can be written as
where I = t3l/12 is the second moment of the cross-section. Denote k2=P/(2EPI),then (18) can be changed into which may be integrated to get where the integration constant can be determined by the continuity condition at point B,i.e., as ϕ=γ*. where γ*= γ+θ and Rγ is the radius of curvature of arc BC at point B,which can be expressed as Substitution of (21) and (22) into (20) gives As ϕ=0,i.e.,for the point H,one has MH=M0+P2n,where n is shown in Fig. 4,then and Substitution of (25) into (23) results in Similarly,introducing λ*=P/P0 and using k2=P/(2EPI),one obtains By denoting the non-dimensional parameter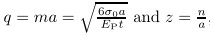 ,the non-dimensional
form of (26) becomes
For z=n/a>0,the positive root of (28) is
3.2 Force analysis of arc BC
,the non-dimensional
form of (26) becomes
For z=n/a>0,the positive root of (28) is
3.2 Force analysis of arc BCConsidering the moment equilibrium of arc BC in Fig. 4(a),one has
where L*=L−n is the arm of force. Then where λ is the non-dimensional load without considering the effect of strain hardening,which is defined in (15). Substituting (29) and (15) into (31) yields (32) can be rewritten as The solution to the above equation is where The non-dimensional displacement δ/a is the same as (16). Similarly,the collapse mode will end as the vertical coordinate of the top hinge C equals zero,and the maximum angle of rotation is the same as (17).4 Numerical examples and discussion 4.1 Finite element model
The simulation of the quasi-static lateral compression on the elliptical tube is performed using the explicit code LS-DYNA. As shown in Fig. 5,the finite element (FE) model consists of a rigid hammer,an elliptical tube and a rigid base. The hammer just moves downwards with a translational displacement in the y-direction,and all the other translations and rotations are fixed. All the degrees of freedom of the rigid base are fixed. The elliptical tube is modeled with solid elements,and the parameters for the elastic linear hardening constitutive relations are listed in Table 1.
 |
| Fig. 5 Finite element model of elliptical tube subjected to quasi-static compression by two parallel rigid plates |
Because the explicit code is adopted to simulate the static problems in this study,the loading
method and the loading time should be carefully selected [13, 14] ,and a loading as smooth as
possible is preferred here to avoid oscillations or incorrect results.
4.2 Comparisons between analytical and FE predictions
The theoretical prediction and FE analysis are conducted for the elliptical tubes with h=1.2, 1.4,and 1.6,as shown in Fig. 6 to Fig. 8. a,t,and l are specified as 40 mm,1.5 mm,and 5 mm,respectively. The strain hardening modulus is set as EP =1500 MPa and 0,respectively, to introduce and neglect the effect of strain hardening,namely,‘the elastic linear hardening model’ and ‘the elastic perfectly plastic model’ in the FE simulations. When introducing the effect of strain hardening in the analytical calculations,γ = 0.6θ,as illustrated in Fig. 4,where γ reflects the size of the plastic zone HB. From Fig. 6 to Fig. 8,it is clear that good agreement is found between the analytical model and the FE analysis.
 |
| Fig. 6 Numerical and theoretical compari-sonofnon-dimensional‘load-displace-ment’ relations non-dimensional ‘load-displacement’ relations for elliptical tube (a=40 mm,h=1.2 |
 |
| Fig. 7 Numerical and theoretical compari-son of non-dimensional ‘load-displace- ment’ relations non-dimensional ‘load-displace-ment’ relations for elliptical tube (a=40 mm,h=1.4) |
 |
| Fig. 8 Numerical and theoretical compari-son of non-dimensional ‘load-displace-ment’ relations non-dimensional ‘load-displace-ment’ relations for elliptical tube (a=40 mm,h=1.6) |
The deformations of an elliptical tube with a=40 mm and h=1.4 are plotted in Fig. 10,the strain hardening modulus is set as EP =1 500 MPa. The deformation process for the elliptical tube under quasi-static lateral compression can be clearly observed.
 |
| Fig. 9 Numerical and theoretical compari-son of non-dimensional ‘load-displace-ment’ relations non-dimensional ‘load-displacement’ relations for elliptical tube (a=40 mm,h=1/1.4) |
 |
| Fig. 10 Deformations predicted by FE simu-lation for elliptical tube (a=40 mm, h=1.4,Ep =1 500 MPa) |
 |
| Fig. 11 Deformations predicted by FE simu-lation for elliptical tube (a=40 mm, h=1/1.4,E p =1 500 MPa) |
 |
| Fig. 12 Numerical and theoretical com-parison of non-dimensional ‘load-displacement’ curve for elliptical tube with a=30 mm,h=1.2 |
Similarly,the FE analysis for an elliptical tube with a=40 mm and h < 1 can be conducted and compared with the analytical predictions. For brevity,only the comparisons and deforma- tions for h=1/1.4 are given in Figs.9 and 11,respectively. The simulation results are in good agreement with those predicted by the analytical model.
4.3 Discussion on γ of arc HBIn the above numerical examples,the horizontal semi-axis a is fixed at 40 mm and only the vertical semi-axis b varies. The parameter γ is always set as 0.6θ. Lots of calculations indicate that γ/θ only depends on a. To verify the conclusion,the non-dimensional load-displacement relations are plotted for a=30 mm and a=20 mm in Figs.12−15,respectively. After lots of tests, γ/θ is found to be 0.7 for a=30 mm and 1.2 for a=20 mm,respectively. From Figs.12−15,it is clear that as γ/θ is specified,the analytical findings are in good agreement with those of the FE analysis for a given value of a.
 |
| Fig. 13 Numerical and theoretical comparison of non-dimensional ‘load-displacement’ curve for elliptical tube with a=30 mm, h=1.4 |
 |
| Fig. 14 Numerical and theoretical com-parison of non-dimensional ‘load-displacement’ curve for elliptical tube with a=20 mm,h=1.2 |
 |
| Fig. 15 Numerical and theoretical comparison of non-dimensional ‘load-displacement’ curve for elliptical tube with a=20 mm, h=1.4 |
 |
| Fig. 16 Numerical results of non-dimen-sional ‘load-displacement’ curves for elliptical tubes with identical horizontal semi-axis (a=40 mm) |
The non-dimensional load-displacement curves in the presence of strain hardening effect obtained from the FE simulations and analytical predictions are plotted in Figs.16 and 17, respectively. It can be seen that as h=1,the elliptical tube degenerates to a circular tube,and the analytical results degenerates to the results of Ref.[5]. For all the elliptical tubes having the same horizontal semi-axis a,their initial collapse loads are identical. From Figs.16 and 17,it is found that for a given δ,the load increases as h decreases,and as a result,the stroke decreases. As h is approximately in the range of 1.2 to 1.4,a relative even and long plateau region is achieved,which is rather good for the design of energy absorbers.
 |
| Fig. 17 Theoretical results of non-dimensional ‘load-displacement’ curves for elliptical tubes with identical horizontal semi-axis (a=40 mm) |
The analytical and FE predictions for the loads of elliptical tubes of the same mass and different semi-axes are plotted in Figs.18 and 19,respectively. A circular tube with R=40 mm is set as the reference tube,the semi-major axis and semi-minor axis of the other two elliptical tubes are 45 and 35 mm,respectively. Their semi-major axis is either parallel or normal to the compression direction. Since the initial collapse load of an elliptical tube is P0 = σ0 t2l/a,the initial collapse loads of the three tubes are different. Obviously,for the reference circular tube, P0c= σ0t2l/R. For contrast,the collapse load and the displacement of the other two elliptical tubes are normalized by P0c and R,respectively. In Figs.18 and 19,γ = 0.5θ for a=45 mm and γ=0.65θ for a=35 mm,respectively. From Figs.18 and 19,one can also find that for the elliptical tubes of the same mass,a relatively even and long plateau region of the load-deflection curves can be obtained when loaded along the major axis of an elliptical tube.
 |
| Fig. 18 Theoretical results of non-dimens-ional ‘load-displacement’ curves for tubes of same mass |
 |
| Fig. 19 Theoretical results of non-dimensional ‘load-displacement’ curves for tubes of same mas |
It is necessary to obtain the load-deflection curves of the tubes under lateral compression for the design of energy absorbers. In this paper,the quasi-static compression of an elliptical tube compressed by two parallel rigid plates is investigated theoretically. A four-hinge mechanism of the elliptical tube is proposed and a hinge line theory is further applied when considering the effect of strain hardening. From both the finite element analysis and the rigid plastic analytical models,it is found that the slightly ovalized tubes with their major semi-axis parallel to the lateral compression direction exhibit fairly good energy absorption behavior. Although only the quasi-static compression of the elliptical tubes is investigated in this paper,the theoretical model is still effective to predict the energy absorption behavior of the elliptical tubes under low-velocity impact.
| [1] | Yu, T. X. and Lu, G. X. Energy Absorption of Structures and Materials (in Chinese), Chemical Industry Press, Beijing (2006) |
| [2] | DeRuntz, J. A. and Hodge, P. G. Crushing of a tube between rigid plates. Journal of Applied Mechanics, 30, 391-395(1963) |
| [3] | Burton, R. H. and Craig, J. M. An Investigation into the Energy Absorbing Properties of Metal Tubes Loaded in the Transverse Direction, Thesis, University of Bristol, England (1963) |
| [4] | Redwood, R. G. Discussion of "Crushing of a Tube Between Rigid Plates". Journal of Applied Mechanics, 31, 357-358(1964) |
| [5] | Reid, S. R., and Reddy, T. Y. Effect of strain hardening on the lateral compression of tubes between rigid plates. International Journal of Solids and Structures, 14(3), 213-225(1978) |
| [6] | Wu, L. and Carney, J. F. Initial collapse of braced elliptical tubes under lateral compression. International Journal of Mechanical Sciences, 39(9), 1023-1036(1997) |
| [7] | Wu, L. and Carney, J. F. Experimental analyses of collapse behaviors of braced elliptical tubes under lateral compression. International Journal of Mechanical Sciences, 40(8), 761-777(1998) |
| [8] | Olabi, A. G., Morrisa, E., Hashmi, M. S. J., and Gilchristb, M. D. Optimised design of nested oblong tube energy absorbers under lateral impact loading. International Journal of Impact Engineering, 35, 10-26(2008) |
| [9] | Morris, E., Olabi, A. G., and Hashmi, M. S. J. Lateral crushing of circular and non-circular tube systems under quasi-static conditions. Journal of Materials Processing Technology, 191, 132-135(2007) |
| [10] | Olabi, A. G., Morris, E., and Hashmi, M. S. J. Analysis of nested tube type energy absorbers with different indenters and exterior constraints. Thin Walled Structures, 44, 872-885(2006) |
| [11] | Baroutaji, A., Morris, E., and Olabi, A. G. Quasi-static response and multi-objective crashworthiness optimization of oblong tube under lateral loading. Thin Walled Structures, 82, 262-277(2014) |
| [12] | Frisch-Fay, R. Flexible Bars, Butterworths, London (1962) |
| [13] | Huang, Z. H., Chen, S. Z., and Bai, Y. Y. Discussion of explicit quasi-static loading methods (in Chinese). Journal of Wuhan University of Technology, 33(6), 122-125(2011) |
| [14] | Wang, Q. C., and Fan, Z. J. Improvement in analysis of quasi-static collapse with LS-DYNA (in Chinese). Mechanics in Engineering, 25(3), 20-23(2003) |
 2015, Vol. 36
2015, Vol. 36






































