Shanghai University
Article Information
- M.CHATTERJEE,A.CHATTOPADHYAY.2015.
- Propagation,reflection,and transmission of SH-waves in slightly compressible,finitely deformed elastic media
- Appl.Math.Mech.-Engl.Ed.,36(8): 1045-1056
- http://dx.doi.org/10.1007/s10483-015-1961-7
Article History
- Received Nov. 16, 2014;
- in final form May 22, 2015
1 Introduction
As a research object,incompressible and slightly compressible anisotropic materials draw attention only recently,which are mostly motivated by interest in the effects of large primary static deformations on dynamical material response.Motivated by the desire to explicate such response,there have been a number of recent papers aiming at explaining the effect of pre-stress on wave propagation in elastic plates,laminates,half-spaces,and other layered structures [1,2,3,4,5,6,7,8,9] . Although stress is often induced in the formation of layers of material by industrial manufacturing processes such as fabrication,a far greater concern within many structures is the stress arising from external loads.However,modern material technology is now capable of producing material able to withstand high loads and suffer large deformation prior to failure.In particular,it is noted that the use of rubber-like components as vibration insulators in bridges and tall buildings has direct relevance to modern methods of earthquake protection [10] .The industrial application of such components is widely spread,including engine mounts,off-shore structure flex-joints and vibration insulators.A particular application,which to some extent motivated theses recent studies,is the increasing use of rubber-like components(slightly compressible). Rogerson[11] emphasized that although surface waves are perhaps most readily associated with earthquakes,they are often observed as a significant contribution to the transient response of plates and laminates to impulsive loads.
It is with such motivations in mind,particularly applied to slightly compressible rubber-like plates and laminatesthat we embark on the present study.Some recent works on this topic have been done by Dhua et al. [12] ,Chattopadhyay and Sahu [13] ,Rogerson et al. [14] ,Sandiford and Rogerson [15] ,and Rogerson and Murphy [16] .
Seismic waves can occur as a result of an earthquake,and mathematical study of seismic waves consists mainly of the study of propagation,reflection,and refraction of elastic waves from discontinuities present inside the Earth.When the waves propagate in an unbounded composite medium consisting of two joined half-spaces of different material properties,one can find an incident wave in conjunction with reflection and refraction at the interface separating the two media.The wave which emanates from infinite depth in one of the media is called the incident wave.In order that the stresses and the displacements are continuous at the interface,a new combination of waves occur which are called the reflected and refracted waves.Without going into details,some of the remarkable research works which may be cited are Knott [17] ,Gutenberg [18] ,Ogden and Sotiropoulos [19,20] ,Chattopadhyay and Rogerson [21] , Chattopadhyay [22,23,24] ,and Chatterjee et al. [25] .
The crust region of our planet is composed of various heterogeneous layers with different geological parameters.Different authors have taken different forms of variation,like harmonic, linear,quadratic,etc.,for simulating the variation in density and other geological parameters inside the Earth.In this problem,heterogeneity has been considered in Case II.
The mathematical study of seismic waves mainly consists of the study of propagation,reflection,refraction of elastic waves from discontinuities present inside the Earth.In this paper, all the phenomena are discussed for SH waves in slightly compressible,finitely deformed elastic media.Since the nature avoids any extremes,the slight compressibility seems to be a more realistic assumption than ideal incompressibility.The complete study of SH wave in slightly compressible,finitely deformed media discussed in this paper is very important in case of geophysical and civil engineering aspects.
2 Governing equations
Consider an elastic solid possessing a natural unstressed isotropic state B0 in a configuration for which the position vector of a representative particle is denoted by XA.An initial primary deformation is imposed on the unstressed state to arrive at a finitely deformed equilibrium configuration,denoted by Be.This particle has a position vector xi(XA).Finally,an infinitesimal time-dependent motion is super-imposed upon the finite deformation B0→Be with the associated position vector of a representative particle in the current configuration Bt denoted by xi(XA,t).The position vector xi(XA,t)can therefore be expressed as
where u is the small time-dependent displacement associated with the secondary deformation Be→Bt.The deformation gradients associated with the deformations B0→Bt and B0→Be are defined through the component relationship respectively.With(1)and(2),it can be shown that the above two deformation gradients are related by with δij being the Kronecker delta,a comma denoting an indication of differentiation with respect to the implied spatial coordinate in Be and an overbar denoting evaluation in Be.It will be assumed that the pre-stress arises from a pure homogeneous strain and therefore F is a constant tensor field.In the absence of body forces,the equations of motion can be written as
with πiA(F,p)denoting the first components of the Piola-Kirchhoff stress tensor,ρ denoting the material density,a superimposed dot differentiation with respect to time,and W(F)isthe strain energy function per unit volume.Throughout this paper,our concern is nearly incompressible elastic materials.It can be shown for materials subject to the internal constraint of incompressibility that J=1,where J=det F(see e.g.Chadwick [26] ).This constraint is relaxed slightly to model cases such that J≈1.Accordingly,an appropriate form of the strain energy function can now be obtained by introducing a Taylor series expansion of the strain energy function around the small order parameter(J−1),namely
Such a form of strain function has been previously employed to elucidate anomalies on the slowness surface of incompressible and nearly incompressible elastic material [27] .Itisnoted that there is no linear term in the expansion of(5).This is because k~O(J−1) −1 ,and therefore,nothing is gained by including a linear term [27] .In the above expansion(4),κis the bulk modulus,which is evaluated at J= 1.Strictly speaking,the bulk modulus is a function of the deformation; however,for rubber-like materials it is found adequate to take the bulk modulus as a constant[28] .In the absence of body forces,the linearised equations governing small-amplitude motion in an elastic material are given by
where J=det F,and B is the fourth-order elasticity tensor defined in component form as The elasticity tensor associated with a strain energy function of the form in(4)is derivable from(3),taking the component form On inserting the form of strain energy indicated in(5)into(6)and(7),we obtain the equation governing small-amplitude motions in a nearly incompressible material as where(B0jilk)is the elasticity tensor associated with the leading-order term W0(F,1)of the strain energy function in(5).A measure scaled incremental surface traction at a point with outward unit normal n in Be is now defined by [3]
Expanding πiA as a Taylor series around the basic state in Be and making use of(3)and(5), a linearized measure of incremental surface traction in a component form is given by 3 Constitutive relationshipsBefore we begin the discussion of this specific problem it is noted that the components of the strain function W0(F,1)appearing in(5)is the form of strain energy function generally associated with the corresponding incompressible elastic material,therefore
where I1 and I2 denote the first two principal invariants of the modified right Cauchy-Green strain tensor C=FTF and trdenotes its trace.Case I Slightly compressible homogeneous layer overlying slightly compressible homogeneous half-space
Here,we consider the problem of SH wave propagation in slightly compressible layer of thickness h overlying a slightly compressible half-space as shown in Fig.1.A Cartesian coordinate system is chosen with axes coincident with the principal axes of deformation in Be,oriented such thatOx1 is horizontal and Ox2 is vertically downwards,where O is the origin.For SH wave,
and u3 is independent of x3. |
| Fig.1 Geometry of problem |
The form of displacement shown in(13)may now be utilized in(9)upon which use of the fact that all non-zero components of the elasticity tensor take one of the three forms B0iijj,B0ijji or B0ijij ,enables the two non-trivial equations of motion for the layer and the half-space to be expressed in the forms of
andSimilarly,the two non-zero components of the incremental tractions for the layer and the half-space are obtained from(11)in the forms of
and4 Solution of problem
The solutions of the equations of motion(14)and(15)can be written in explicit forms of
and Substituting(18)and(19)in(14)and(15),we have and5 Boundary Conditions
(i)The upper surface is stress free,i.e.,
(ii)the stresses are continuous at the interface,i.e.,
(iii)the displacement components are continuous at the interface,i.e.,
Satisfying the boundary conditions(22),(23)and(24),a homogeneous system of three equations in three unknowns is obtained.Eliminating the unknowns,we obtain the Dispersion relationship as
whereIf in the isotropic case,μ1 and μ2 be the rigidities of the upper layer and the half-space respectively,then
Putting the above values in(25),the dispersion relationship for SH wave in isotropic medium can be obtained as

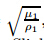 ,and v2=
,and v2=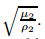
Case-II Slightly compressible inhomogeneous layer overlying slightly compressible homogeneous half-space
The equations of motion for the inhomogeneous layer and the homogeneous half-space are
where γ is the inhomogeneity parameter having a dimension of inverse of length.In a similar manner,the two non-zero components of the incremental tractions for the layer and the half-space are
and Substituting(18)and(19)into(28)and(29),we obtain and The solutions have been written in the forms of Substitution from(32)to(34)in(22)to(24)gives6 Reflection and refraction of SH wave at interface
In this section,the reflection and transmission of SH waves at the interface of two half-spaces of slightly compressible,finitely deformed elastic media are studied(see Fig.2).Let the two half-spaces be in contact along the plane x2=0 and x2-axis be positive downwards in the lower half-space.The SH wave incident at the interface from the lower half-space H will give rise to a reflected SH wave in the same half-space H and a transmitted SH wave in the upper half-space H' .Let the angles at the interface made by the incident,reflected and transmitted waves be θ0,θ1 and θ2 respectively.The reflected and transmitted waves are denoted by superscripts α=1,2 with α= 0 corresponding to incident wave.The displacement and the non-zero component of incremental traction associatedwith these three waves may be represented in the forms of
and in which Aα denote the amplitudes of waves travelling with speed Cα,wave number kα in a direction specified by the unit vector p (α). For incident plane SH wave, For reflected SH waves, For transmitted SH waves, |
| Fig.2 Geometry of reflection and refraction |
7 Boundary Conditions
For the physically most significant case of perfect contact,the displacements and stresses are continuous at the interface,i.e.,at x2=0.
The boundary conditions are
andUsing the boundary conditions(41)and(42),we have
(43)and(44)must hold for all x1 and t.Therefore it is deduced that andUsing(45)and(46),(43)and(44)become
andThe reflection and refraction coefficients can be obtained by solving(47)and(48)to yield
and8 Slowness sections
To determine the precise nature of the reflected and refracted waves,we need to consider the slowness section associated with the(x1,x2)-plane.To this end,we take solution of(14)in the form
in which the slowness vector s is defined by sm=pmv −1 (m=1,2).If the solution of the form(51)is inserted into(14)the condition that the homogeneous system admits a non-trivial solution yields the equation of the associated slowness section,i.e., We shall now specify the strain energy function W0(F,1)to the Neo-Hookean strain-energy function within which λ1,λ2,λ3 are principal stretches,k'=k −2/3μ,where μ and k'(often denoted by λ) are the Lame moduli and k is the bulk modulus of the material in the un-stressed configuration (see Ogden [28] ).For this strain-energy function,we have [14]In Fig.3,the plots of the slowness section(52)are presented with respect to the two states of pre-stress.The first pre-stresses state associated with curve 1 illustrates an example,for which the slowness section is essentially elliptic in nature with its major axis along the s2-axis. Curve 2 is associated with the second pre-stresses state and illustrates an example for which the slowness section is also elliptic in nature,but its major axis is along the s1-axis.From the two sets of values,it is also seen that,as the values of λi(i=1,2,3)andμdecrease,the area of the ellipse representing the slowness section also decreases.
 |
| Fig.3 Plots of slowness sections associated with(52)for Neo-Hookean material[14] with(1)λ1 = 1.7,λ2=2.0,λ3=1.6,μ=1.0;(2)λ1=1.1,λ2=0.91,λ3=1.0,μ=0.7 |
9 Numerical results and discussion
(35)gives the dispersion equation for SH waves propagating in a slightly compressible nonhomogeneous layer overlying a slightly compressible homogeneous half-space.This equation is very helpful in order to study the effects of inhomogeneity and wave number on the phase velocity of SH waves.For the layer and the half-space(as in Fig.1),the following data are taken from Ref.[14]:
In Fig.4,the dimensionless phase velocity v/v1 has been plotted against the dimensionless wave number kh for different values of inhomogeneity parameter of the layer.From the figure, it is observed that the phase velocity v/v1 decreases monotonically with the increase in kh1. Also in the presence of the inhomogeneity the phase velocity decreases and the effect is very prominent.In this figure,curve 1 represents the case I,i.e.,the upper layer is homogeneous.
 |
| Fig.4 Dimensionless phase velocity against dimensionless wave number when v1/v2=1.1 |
The variations of reflection and refraction coefficients against incident angle for Neo-Hookean strain-energy function are shown in Figs 5 and 6 using the two sets of data in(55).
 |
| Fig.5 Amplitude ratios of reflected SH waves against incident angle θ0 |
In Fig.5,curve I corresponds to reflection coefficient of SH wave in slightly compressible media.All the values of curve I are positive except from 87◦ to 90◦.In the isotropic case (denoted by curve II),the values of A1/A0 are all positive except from 76◦ to 90◦.The differences of values in slightly compressible case compared with those of the isotropic case decreases monotonically from θ=0◦ to θ=90◦ .
In Fig.6,the refraction coefficients of SH waves for a slightly compressible medium(curve I)at different angles of incidence have been plotted along with the curve for isotropic medium (curve II).The values of A2/A0 are all positive for curves I and II within the whole range θ◦∈[0◦,90◦].The difference in values of the curves decreases continuously for 0 ◦≤θ◦≤90◦ i.e.the difference is seen maximum at θ=0◦ and minimum at θ=90◦ .
 |
| Fig.6 Amplitude ratios of refracted SH waves against incident angle θ0 |
10 Conclusions
We have considered both homogeneous and inhomogeneous slightly compressible,finitely deformed media for SH wave propagation.The dispersion relationships have been obtained in a closed form.The dimensionless phase velocity has been plotted against dimensionless wave number.It has been observed that the dimensionless phase velocity decreases with both the increase of dimensionless wave number and the dimensionless inhomogeneity parameter. The reflection and refraction coefficients are shown graphically for both slightly compressible medium and isotropic medium.Comparing the two cases,it is observed that the values of the reflection and refraction coefficients in slightly compressible medium are higher than the same in isotropic medium.However,the difference in values decreases continuously within the range θ◦∈[0◦,90◦].
Acknowledgements The authors convey their sincere thanks to Indian School of Mines,Dhanbad, for providing fellowship to Miss M.CHATTERJEE and also facilitating us with best facilities.The valuable suggestions made by the reviewers are highly appreciated and thankfully acknowledged.| [1] | Dowaikh,M.A.and Ogden,R.W.On surface waves and deformations in a pre-stressed incompressible elastic solid. IMA Journal of Applied Mathematics,44,261-284(1990) |
| [2] | Rogerson,G.A.and Fu,Y.B.An asymptotic analysis of the dispersion relation of a pre-stressed incompressible elastic plate. Acta Mechanica,111,59-77(1995) |
| [3] | Rogerson,G.A.and Sandiford,K.J.On small amplitude vibrations of pre-stressed laminates. International Journal of Engineering Science,34(8),853-872(1996) |
| [4] | Ogden,R.W.and Sotirropoulos,D.A.On interfacial waves in pre-stressed layered incompressible solids. Proceedings of the Royal Society A,450,319-341(1995) |
| [5] | Qian,Z.H.,Jin,F.,Lu,T.J.,Kishimoto,K.,and Hirose,S.Effect of initial stress on Love waves in a piezoelectric structure carrying a functionally graded material layer. Ultrasonics,50(1),84-90(2010) |
| [6] | Qian,Z.H.,Jin,F.,Lu,T.J.,and Kishimoto,K.Transverse surface waves in a 6 mm piezoelectric material carrying a prestressed metal layer of finite thickness. Applied Physics Letters,94(9),093513(2009) |
| [7] | Qian,Z.H.,Jin,F.,Kishimoto,K.,and Lu,T.J.Propagation behavior of Love waves in a functionally graded half-space with initial stress. International Journal of Solids and Structures,46(6),1354-1361(2009) |
| [8] | Jin,F.,Qian,Z.H.,Wang,Z.,and Kishimoto,K.Propagation behavior of Love waves in a piezoelectric layered structure with inhomogeneous initial stress. Smart Materials and Structures,14(4),515-523(2005) |
| [9] | Qian,Z.H.,Jin,F.,Kishimoto,K.,and Wang,Z.Effect of initial stress on the propagation behavior of SH-waves in multilayered piezoelectric composite structures. Sensors and Actuators A:Physical,112(2-3),368-375(2004) |
| [10] | Sheridan,P.M.,James,F.O.,and Miller,T.S.Design of Components,Engineering with Rubber,Hanser,Munich,209-235(1992) |
| [11] | Rogerson,G.A.Penetration of impact waves in a six-ply fibre composite laminate. Journal of Sound and Vibration,158,105-120(1992) |
| [12] | Dhua,S.,Chattopadhyay,A.,and Sahu,S.A.Propagation of surface wave in a fluid layer overlying a slightly compressible,finitely deformed elastic medium.Journal of Vibration and Control(2014)DOI:10.1177/1077546314520836 |
| [13] | Chattopadhyay,A.and Sahu,S.A.Stresses produced in slightly compressible,finitely deformed elastic media due to a normal moving load. Archive of Applied Mechanics,82,699-708(2012) |
| [14] | Rogerson,G.A.,Sandiford,K.J.,and Prikazchikova,L.A.Abnormal long wave dispersion phenomena in a slightly compressible elastic plate with non-classical boundary conditions. International Journal of Non-Linear Mechanics,42,298-309(2007) |
| [15] | Sandiford,K.J.and Rogerson,G.A.Some dynamic properties of a pre-stressed,nearly incompressible(rubber-like)elastic layer. International Journal of Non-Linear Mechanics,35,849-868(2000) |
| [16] | Rogerson,G.A.and Murphy,J.G.Surface waves in slightly compressible,finitely deformed elastic media. Mechanics Research Communications,25(5),493-502(1998) |
| [17] | Knott,C.G.Reflection and refraction of elastic waves with seismological applications. Philosophical Magazine,48,64-97(1899) |
| [18] | Gutenberg,B.Energy ratio of reflected and refracted seismic waves.Bulletin of the Seismological Society of America,34,85-102(1944) |
| [19] | Ogden,R.W.and Sotiropoulos,D.A.The effect of pre-stress on the propagation and reflection of plane waves in incompressible elastic solids. IMA Journal of Applied Mathematics,59,95-121(1997) |
| [20] | Ogden,R.W.and Sotiropoulos,D.A.Reflection of plane waves from the boundary of a prestressed compressible elastic half-space. IMA Journal of Applied Mathematics,61,61-90(1998) |
| [21] | Chattopadhyay,A.and Rogerson,G.A.Wave reflection in slightly compressible finitely deformed elastic media. Archive of Applied Mechanics,71,307-316(2001) |
| [22] | Chattopadhyay,A.Wave reflection and transmission in triclinic crystalline medium. Archive of Applied Mechanics,73,568-579(2004) |
| [23] | Chattopadhyay,A.Wave reflection in triclinic medium. Archive of Applied Mechanics,76,65-74(2006) |
| [24] | Chattopadhyay,A.Reflection for three dimensional plane waves in triclinic crystalline medium.Applied Mathematics and Mechanics(English Edition),28,1573-2754(2007)DOI:10.1007/s10483-007-1004-y |
| [25] | Chatterjee,M.,Dhua,S.,Sahu,S.A.,and Chattopadhyay,A.Reflection in a highly anisotropic medium for three-dimensional plane waves under initial stresses. International Journal of Engineering Science,85,136-149(2014) |
| [26] | Chadwick,P.Continuum Mechanics:Concise Theory and Problems,Allen and Unwin,London(1976) |
| [27] | Scott,N.H.The slowness surface of incompressible and nearly incompressible elastic materials. Journal of Elasticity,16,239-250(1986) |
| [28] | Ogden,R.W.Non-linear Elastic Deformations,Ellis Horwood,New York(1984) |
 2015,Vol.36
2015,Vol.36

























































