Shanghai University
Article Information
- Yang SONG,Chunxiao XU,Weixi HUANG,Guixiang CUI.2015.
- Optimal transient growth in turbulent pipe flow
- Appl.Math.Mech.-Engl.Ed.,36(8): 1057-1072
- http://dx.doi.org/10.1007/s10483-015-1963-7
Article History
- Received Sept. 14, 2014;
- in final form Dec. 5, 2014
1 Introduction
Coherent structures play a key role in wall turbulence.Since the experimental work of Kline et al. [1] ,there have been many meaningful results achieved on the turbulent coherent structures in the past several decades.With a large amount of experiments and numerical simulations,it is well recognized that there are two main and distinguished coherent structures which dominate the flow in the buffer layer [2] .They are low speed streaks and streamwise rolls with a statistical spacing of 100 wall units.Nagata [3] and Waleffe [4,5] obtained the exact solutions in channel flow which suggested a traveling wave in the near wall region and led to a self sustained process (SSP) [6] .In this view,streamwise rolls generate and strengthen the streaks with the lift-up mechanism[7] .Then,the streaks form the streamwise waves through an instability effect.At last,with the nonlinear interaction,the streamwise waves induce the streamwise rolls.This SSP was discussed in detail by Farrell and Ioannou [8] .
Although flow physics in the buffer layer seems to be already clear,the situation becomes much more complex in the logarithmic region[9] .Recently the so-called very large scale motions (VLSMs)and superstructures observed in experiments at high Reynolds numbers were found to contribute half of the total turbulent kinetic energy in the logarithmic region [10] .These structures are quite different from streaks in the buffer layer for their different spacings and dependence on flow geometries.Marusic et al. [11] proposed that the VLSMs affect the structures in the buffer layer through superposition and modulation mechanisms.However,it is still a question where the VLSMs come from.
An alternative view to this question is the unstable or slightly damped modes of the turbulent velocity profile which cause the production of streaks.This process can be modeled by the linearized Navier-Stokes equaions with the linear stability theory.But the linear stability analysis is not enough,since even stable perturbations can undergo a transient amplification before decaying [12] .The main reason for this phenomenon is the non-orthogonality of the eigenvectors of the linear system as pointed out by Schmid and Henningson [13] .The interaction of modes yields the transient growth process.
The optimal transient growth processes in different flow geometries have been widely studied. In the previous studies,the optimal transient growth structures gave an explanation of the origin of the structures in fully developed turbulence or transition scene.The optimal streaks in turbulent channel flow were computed by Butler and Farrell [14] using the Reynolds and Tiederman’s turbulent mean velocity profile [15] with molecular viscosity,and they found the streaks spacing λz ≈3h,where h is the channel half width.In the later context,del Alamo and Jimenez [16] and Puials et al. [17] computed the problem using the same model as Butler and Farrell’s with eddy viscosity suggested by Cess [18] .In their analysis,besides the main optimal streaks,there is a secondary peak which scales 100 wall units.This structure represents the streaks in the buffer layer observed in the previous experiments and numerical simulations. After that,Willis et al.[19] also computed the optimal transient growth of perturbations in a turbulent pipe flow using original variables(velocities and pressure).Their method has a simple expression but the computational cost is relatively high. In this paper,the optimal transient growth process of perturbations with an eddy viscosity model in a turbulent pipe flow is considered using a different numerical method from that of Willis et al.[19] .This method is derived by projecting the Reynolds averaged Navier-Stokes (RANS)equations onto the subspace of radial vorticity and radial velocity in a cylindrical coordinate system.Then,we derive the linearized perturbation equations and analyze the optimal transient growth process of perturbations.Relations of the optimal structures with the structures obtained from experiments and other analysis are discussed.This paper is organized as follows.In Section 2,a linear stability model of turbulent pipe flow is formulated together with the numerical method.Then,in Section 3,we test our model and numerical method using a laminar case.The results are compared with the previous studies.We focus on the optimal transient growth process in turbulent pipe flow in Section 4.Finally,conclusions are drawn in Section 5.
2 Model formulation and numerical method
2.1 Model formulation
In the following,we consider turbulent motion of an incompressible viscous fluid with kinematic viscosity ν and density ρ in a pipe.The geometry of the flow is shown in Fig.1.Naturally, the cylindrical coordinate system(r,θ,z)is used,which denotes the radial,azimuthal,and axial directions,respectively,and the corresponding velocity components are u,v and w.The base flow denoted by(U,P)obeys the RANS equations with an eddy viscosity model as follows:
where the total viscosity is νT =ν+νt with the molecular viscosity ν and the eddy viscosity coefficient νt.The Reynolds number is defined as Re=UcR/ν,where Uc is the centre-line velocity,and R is the radius of pipe.Considering a small perturbation denoted by(u',p'),the dimensionless linearized perturbation equations can be derived from(1)with a non-constant viscosity coefficient, |
| Fig.1 Geometrical model of pipe flow |
The linearized perturbation equations together with the continuity equation are complete. Instead of solving the system of original variables(velocities and pressure),we project the linearized perturbation equations onto the subspace of radial vorticity and radial velocity by using the projection operators Pωr and Pu,which are defined as follows[4]:
Then,the perturbation equations of ω'r and u'are obtained,Terms in the above equations can be simplified by using the definition of ω'r and continuity equation,
Thus,this fourth-order differential equation system is complete for ω'r and u'.2.2 Numerical method
A modified Chebyshev-Fourier method is used to solve the fourth-order differential equation system(see(4)).Firstly,the perturbations ω'r and u' are expanded by the Fourier spectral approximation.A periodic boundary condition is considered in the streamwise and azimuthal directions as follows:
Here and in the following,the prime is omitted for simplicity.K and N are the truncated wave numbers.This approximation leads to the linear ordinary differential equations of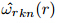 and
and 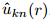 ,
where the linear differential operators Aij and Bij
are defined as follows:
Here,Di(i=0,1,2,3,4)is the ith-order differential operator,and W represents the streamwise
velocity of the base flow,which is a function ofr(W=W(r)).These operators are based on the RANS equations.When considering the molecular viscosity only,the above equations can
be simplified and become a linear combination of those suggested by Burridge and Drazin
[20],which are expressed by the variables,
,
where the linear differential operators Aij and Bij
are defined as follows:
Here,Di(i=0,1,2,3,4)is the ith-order differential operator,and W represents the streamwise
velocity of the base flow,which is a function ofr(W=W(r)).These operators are based on the RANS equations.When considering the molecular viscosity only,the above equations can
be simplified and become a linear combination of those suggested by Burridge and Drazin
[20],which are expressed by the variables,
The boundary conditions for the fourth-order differential system can be divided into two
parts.One is the wall condition and the other is the centre condition.At wall,the no-slip
condition,i.e.,v= 0,is applied.Considering the incompressibility of fluid,we get u=0, =0,and ωr = 0 at wall.The centre condition can be derived from
=0,and ωr = 0 at wall.The centre condition can be derived from  = 0.However,
the symmetry of perturbations is involved in the derivation,so the expressions of the centre
condition are different for the perturbations with a different wave number n,i.e.,
= 0.However,
the symmetry of perturbations is involved in the derivation,so the expressions of the centre
condition are different for the perturbations with a different wave number n,i.e.,
The ordinary differential equation(7)is solved by a modified Chebyshev method in which
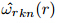 and
and 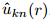 can be expanded by
can be expanded by


The turbulent base flow profile is always linearly stable in pipe.In other words,all the perturbations decay exponentially when the time is large enough.However,there is a transient growth process because of the nonorthogonality of the modes.This process allows that a small perturbation of a specific scale can be amplified so that the nonlinear effect becomes significant. To quantify such a process,the transient growth amplification G(t;k,n)is defined as
where E(t;k,n)is the kinetic energy of the perturbations at a given timet.Then,the maximum transient growth amplification is defined as Gmax(k,n)=supt G(t;k,n).According to the spectral decomposition of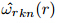 and
and 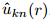 ,the energy E can be computed as(the symbol *
denotes complex conjugate in the following expression)
,the energy E can be computed as(the symbol *
denotes complex conjugate in the following expression)
We rewrite the eigenvalue problem by σmAxm=Bxm.Here,(σm)and X=(xm)are the sets of eigenvalues and eigenvectors sorted by the real part of eigenvalues.The general solution of the eigenvalue problem can be written as
Then,the general solution q(t) is put into the definition of energy function E(t;k,n)in(13), Here,the Hermite matrix M is associated with the modified Chebyshev method.We rewrite F* F =X*MX and Q=FeΣtF−1.The transient growth amplification in(12)is then expressed as Here,the vector β is defined by 
3 Laminar base flow
In this section,we test our numerical method by considering the linear stability and the optimal transient growth of perturbations in a laminar pipe flow.The results are compared with the previous studies.
3.1 Linear stability of laminar base flow
For a laminar flow in pipe,the total viscosity coefficient is constant,since only the molecular viscosity is present.Thus,the linearized perturbation equations derived in Section 2 become simpler by ignoring



 |
| Fig.2 Relative error of first 200 eigenvalues sorted by their real part with different grid numbers at Re= 3 000,n=0,and k=1 |
 |
To give more details,we study the spectrum distribution of eigenvalues(see Fig.3)and their associated eigenvectors(see Fig.4).Figure 3 shows clearly three distinguished branches which represent different modes(wall mode,centre mode(CM),and mean mode(MM)).All the three modes have their own properties.For the wall mode,it decays slowly with a relative smaller phase velocity.The centre mode has also a slow decay rate but its phase velocity is the largest.For the mean mode,it has a moderate phase velocity and decays rapidly.The eigenvectors shown in Fig.4 are typical fields ofthe three modes.These results are consistant with the previous results of Meseguer and Mellibovsky [23] .
 |
| Fig.3 Transient energy amplification curves at Re= 3 000,k=0,and n=1,2,3,4((S)represents results of Schmid Henningson [22] ,and(M)represents our results) |
 |
| Fig.4 Spectrum of eigenvalues for Re= 3 000,k=1,and n= 1,where three dots represent typical modes,WM,CM,and MM |
3.2 Optimal transient growth process of laminar base flow
The computational method for the transient growth of perturbations with a laminar base flow described in Subsection 2.3 is tested.We compute the time histories of the transient growth amplification,i.e.,G(k,n;k)~t,at Re= 3 000,k=0,and n=1,2,3,4,which were also presented by Schmid and Henningson [22] who used the equations suggested by Burridge and Drazin [20] .As shown in Fig.5,our results show excellent agreement with those of Schmid and Henningson,thus validating the present method.
 |
| Fig.5 Eigenvectors of three typical modes,(a)CM,(b)WM,and(c)MM(fields on left column are velocity vectors projected onto cross section,and right column are contours of streamwise velocity) |
4 Turbulent base flow
The results of the optimal transient growth analysis for the turbulent pipe flow with an eddy viscosity model are presented in this section.Firstly,we give a detailed description of the parameters setup in computation,as suggested by Willis et al. [19] .Then,the transient growth amplifications of perturbations at different Reynolds numbers are computed and discussed.At last,we focus on the relation between the obtained optimal structures and coherent structures observed in experiments,and the self-similar properties in the transient growth process.
4.1 Turbulent mean velocity profile
In the following,we consider the linearized perturbation equations based on the RANS equations(see Subsection 2.1).Here,the eddy viscosity in the viscosity term can be modeled as follows(originally suggested by Cess [18] ):
Here,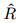 =Re/2,
=Re/2,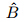 =−2∂zP,and the von Karman constant k=0.42.Using the RANS
equations(1),the base flow(U,P)can be computed.The parameter A+
is adjusted to fit
the turbulent mean velocity profiles from experiments or DNS data.In our computation,we
choose the superpipe experimental data to adjust the parameter A+
in the Cess model.Five
sets of superpipe data
[24]
at different Reynolds numbers are picked out.The corresponding
mean velocity profiles computed by the Cess model are shown in Fig.6 and compared with the
experimental data.
=−2∂zP,and the von Karman constant k=0.42.Using the RANS
equations(1),the base flow(U,P)can be computed.The parameter A+
is adjusted to fit
the turbulent mean velocity profiles from experiments or DNS data.In our computation,we
choose the superpipe experimental data to adjust the parameter A+
in the Cess model.Five
sets of superpipe data
[24]
at different Reynolds numbers are picked out.The corresponding
mean velocity profiles computed by the Cess model are shown in Fig.6 and compared with the
experimental data.
 |
| Fig.6 Turbulent mean velocity obtained by integrating momentum equation with Cess model and its comparison with superpipe data at different Reynolds numbers(lines represent computed results(M),and symbols denote superpipe data(S)) |
4.2 Optimal transient growth process of turbulent base flow
To begin with,we test the grid convergence for the computation of eigenvalues of the high Reynolds number turbulent base flow.Figure 7 shows that the convergence of the eigenvalues can be satisfied,although the error increasing occurs at a smaller index j ≈120 compared with the laminar base flow case of Re= 3 000.After that,the maximum transient growth amplification Gmax in the transient growth process at four typical Reynolds numbers ranging from 20 000 to 250 000,corresponding to the superpipe data,is shown in Fig.8.This figure, shows the dependence of Gmax on the streamwise wave number k and the azimuthal wave numbern.There are two peaks of Gmax with varying n,which represent two optimal structures in the transient growth process.They are quite similar with the results obtained in channel flow [17] .The maximum transient growth amplifications at different Reynolds numbers exist in the region defined by k<n.The peak around n= 1 represents a large scale flow structure which is known as the outer peak structure.The outer peak is fixed on n= 1 with the varying Reynolds number.A similar phenomenon is that the outer peak of Gmax in turbulent channel flow is also a constant(λz≈3h,see Pujals et al. [17] )scaled by the channel half-width h.These phenomena in channel and pipe flows show that the outer peak is dependent on the specific flow geometry.Besidesthe outer peak at n= 1,a weak but distinguishable peak appears at high wave numbers.This peak stands for a relatively small scale motion and itstypical scale becomes smaller as the Reynolds number increases.The appearance of this inner peak indicates that some perturbations of specific large wave numbers can undergo a significant transient growth process.
 |
| Fig.7 Error of first 200 eigenvalues sorted by their real part with different grid numbers M at Re= 240 582,k=0,and n=1 |
 |
| Fig.8 Contours of Gmax at different Reynolds numbers |
In Fig.9,the velocity fields corresponding to the outer peak at Re= 110555 are shown.The two fields in the figure stand for the optimal initial velocity field and the amplified velocity field (when the transient growth amplification of the initial perturbations attains its maximum).It is shown clearly that streamwise rolls and coherent streaks dominate the velocity fields in the pipe.In the initial velocity field,there is a pair of strong streamwise rolls with opposite rotation, leading to a pair of weak streaks.The streaks in the amplified velocity field become much stronger,indicating that a transient growth process causes energy transfer from streamwise rolls to streaks.In other words,it is an alternative mechanism to strengthen streaks.A similar mechanism was also found in turbulent channel flow by Deng et al.[25] .It is worth noting that the outer peak gives a kind of large scale structures but these structures are still different from the VLSMs observed in experiments of internal flow.In pipe flow,the outer peak appears at n= 1,but the experimental research of Bailey and Smits [26] showed that the large scale streaks have a typical scale of about n= 3.This difference indicates that the model of the optimal transient growth process may miss some necessary symmetry limit of perturbations.
 |
| Fig.9 Optimal initial field(a)and amplified velocity field(b)of k=0,n=1 at Re= 110 555 (contours represent streamwise velocities,and vectors are velocities projected to cross section) |
Next,the velocity fields at the inner peak are shown in Fig.10.Similar to the outer peak,the transient growth process causes energy transfer from streamwise rolls to streaks in the buffer layer.In other words,the flow dominated by streamwise rolls becomes the streaky flow in the buffer layer.This process is known as a part of SSP proposed by Hamilton et al. [6] .When measured by the viscosity length δv,the spacing of the steaks in the buffer layer at Re= 110555 is about 100δv(see Fig.10).It is consistent with the results observed in experiments and DNS. In channel flow,almost the same flow structures are found [25] .A reasonable explanation is that the curvature of pipe does not influence the flow in the buffer layer sufficiently,so the amplified velocity field in the buffer layer seems to be independent of geometry.The property of the inner peak is quite different from the outer peak.
 |
| Fig.10 Optimal initial field(a)and amplified velocity field(b)of k=0 and n= 280 at Re= 110 555 (contours represent streamwise velocity,and vectors are velocity projected to cross section, l+θ=θR/δv) |
Another question is the Reynolds number effect on the maximum transient growth amplifications(Gmax)of perturbations.The dependences on the Reynolds number of the inner peak and the outer peak are not the same at different Reynolds numbers,as shown in Fig.11.The outer peak always appears at n= 1,indicating that the corresponding optimal velocity fields are always a pair of streamwise rolls and streaks in the pipe.Moreover,the magnitude of Gmax becomes larger as the Reynolds number increases.It implies that the perturbations become less stable when the Reynolds number increases.The optimal azimuthal wave number n of the inner peak increases with the Reynolds number.However,when measured by the inner length scale(δv),the spacing of streaks corresponding to the inner peak becomes a constant about 100δv(see Fig.11(b)).This phenomenon indicates that the optimal transient growth process at the inner peak in the buffer layer can exist at relatively high Reynolds numbers,and so does the SSP.
 |
| Fig.11 Distribution of maximum transient growth amplifications for k= 0 at different Reynolds numbers(curves are plotted with(a)outer length scale δ and(b)inner length scale δv) |
The streaky flow in the buffer layer can be regarded as a result of the optimal transient growth process of perturbations.However,this process cannot explain the appearance of large scale motions observed in experiments.Actually,in the model we hare computed,the eddy viscosity coefficient represents the dissipation of nonlinear interaction influence on the mean flow.When considering the perturbation of a specific wave number,the dissipation effect is quite different from that denoted by the eddy viscosity coefficient.Therefore,it seems that the errors at low wave numbers are larger.In addition,the magnitude of Gmax at the inner peak is much smaller than that at the outer peak.However,it does not assure that the transient growth of the inner peak structures is weaker than the outer ones.
Finally,the optimal time of the transient growth process is considered,which denotes the time when Gmax is reached.In Fig.12,the transient growth amplification G is shown as a function of t+ and n at different Reynolds numbers(axial wave number k is set to be 0).We can see that the optimal times for the inner peak and the outer peak are quite different,and the difference becomes larger when the Reynoldsnumber increases.It shows that the optimal time of the inner peak is constant about t+≈12.Although the optimal time of the outer peak measured by inner variables becomes larger,it is also independent of the Reynolds number if measured by the outer variables(Uc,R)and is about 40~50.When considering the transient growth process of perturbations of a different wave numbern,the small scale perturbations grow faster than the large ones,and their transient growth amplifications quickly reach the maximum.
 |
| Fig.12 Transient energy amplification G at different n and t+ (streamwise wave number k is fixed at 0) |
After that,small scale perturbations decay while the large ones still grow for longer time. If the energy amplifications of small scale perturbations are large enough,the nonlinear interactions between the small scale fluctuations and the large scale ones become so important that the eddy viscosity cannot exactly represent the nonlinear effect.It is a possible reason why the outer peak cannot explain the appearance of thelarge scale motions observed in experiments.
Furthermore,the optimal time t+ of different scales has a roughly inversely proportional relationship with the wave number n,
where C is a function of the Reynolds number only.This is an interesting finding,as also observed in channel flow [16] .Infact,n represents the wave number,and t+ is inversely proportional to the circular frequency.So the constant C can be regarded as a characteristic velocity of the growth process.It is found that this velocity is constant for different scales,i.e.,the transient growth processes of different scales are selfsimilar.It leads us to relate the present result with the energy transfer cascade of turbulence,where the energy transport rate is constant in the inertial sublayer.5 Conclusions
In this paper,we proposed a new numerical method,which is based on the projected linear stability equations with an eddy viscosity coefficient,to compute the optimal transient growth process of the turbulent pipe flow.A couple of laminar flow cases were computed to test the present method,and the results agreed well with the previous studies.
The transient growth analysis based on the turbulent mean velocity profile was given and compared with the experimental results.Two peaks of the maximum transient growth amplification Gmax with different azimuthal wave numbers were found.The outer peak occurs always at the azimuthal wave number n= 1,while the location of the inner peak is independent of the Reynolds number when measured by the inner variables.The spacing of the velocity streaks corresponding to the inner peak is about 100δv in the buffer layer,consistent with the experimental observations.Thus,the optimal transient growth of perturbations can be an alternative mechanism of the generation of streaks and also an important part of SSP in the buffer layer. Moreover,the scale of the optimal streaks corresponding to the outer peak are different from the VLSMs.This difference may be attributed to the nonlinear interaction between small scales and large scales which cannot be included in the eddy viscosity model.Finally,the optimal time of perturbations of different azimuthal wave numbers was found to be in proportion to the azimuthal wave length.It indicates that the characteristic velocity of different scales is only dependent on the Reynolds number,implying a self-similarity of different scales in the transient growth process.
| [1] | Kline,S.J.,Reynolds,W.C.,Schraub,F.A.,and Runstadler,P.W.The structure of turbulent boundary layers. Journal of Fluid Mechanics,30(4),741-773(1967) |
| [2] | Jimenez,J.and Moser,R.What are we learning from simulating wall turbulence. Philosophical Transactions of the Royal Society A,365,715-732(2007) |
| [3] | Nagata,M.Three-dimensional finite-amplitude solutions in plane Couette flow:bifurcation from infinity. Journal of Fluid Mechanics,217,519-527(1990) |
| [4] | Waleffe,F.Homotopy of exact coherent structures in plane shear flows. Physics of Fluids,15(6),1517-1534(2003) |
| [5] | Waleffe,F.Exact coherent structures in channel flow. Journal of Fluid Mechanics,435,93-102(2001) |
| [6] | Hamilton,J.M.,Kim,J.,and Waleffe,F.Regeneration mechanisms of near-wall turbulence structures. Journal of Fluid Mechanics,287,317-348(1995) |
| [7] | Moffatt,H.K.The interaction of turbulence with strong wind shear. Proceedings of the URSⅡUGG Colloquium on Atoms,Turbulence and Radio Wave Propation,Nauka,Moscow(1967) |
| [8] | Farrell,B.F.and Ioannou,P.J.Dynamics of streamwise rolls and streaks in turbulent wallbounded shear flow. Jounal of Fluid Mechanics,708,149-196(2012) |
| [9] | Jimenez,J.and Hoyas,S.Turbulent fluctuations above the buffer layer of wall-bounded flow,Journal of Fluid Mechanics,611,215-236(2008) |
| [10] | Marusic,I.,McKeon,B.J.,and Monkewitz,P.A.Wall-bounded turbulent flows at high Reynolds numbers:recent advances and key issues. Physics of Fluids,22(6),065103(2010) |
| [11] | Mathis,R.,Hutchins,N.,and Marusic,I.Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. Jounal of Fluid Mechanics,628,311-337(2009) |
| [12] | O'Sullivan,P.L.and Breuer,K.S.Transient growth in circular pipe flow,linear disturbances.Physics of Fluids,6(11),3643-3651(1994) |
| [13] | Schmid,P.J.and Henningson,D.S.Stability and Transition in Shear Flows,Springer,New York(2001) |
| [14] | Butler,K.M.and Farrell,B.F.Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Physics of Fluids,5(3),774-777(1993) |
| [15] | Reynolds,W.C.and Tiederman,W.G.Stability of turbulent channel flow,with application to Malkuss theory. Jounal of Fluid Mechanics,27(2),253-272(1967) |
| [16] | del Alamo,J.C.and Jimenez,J.Linear energy amplification in turbulent channels.Jounal of Fluid Mechanics,559,205-213(2006) |
| [17] | Pujals,G.,Villalba,M.G.,Cossu,C.,and Depardon,S.A note on optimal transient growth in turbulent channel flows. Physics of Fluids,21(1),015109(2009) |
| [18] | Cess,R.D.A Survey of the Literature on Heat Transfer in Turbulent Tube Flow,Westinghouse Research,Resarch Report No. 8-0529-R24(1958) |
| [19] | Willis,P.A.,Hwang,Y.Y.,and Cossu,C.Optimally amplified large-scale streaks and drag reduction in turbulent pipe flow. Physical Review E,8(23),336-354(2010) |
| [20] | Burridge,D.M.and Drazin,P.G.Comments on 'Stability of Pipe Poiseuille Flow'. Physics of Fluids,12,264-265(1969) |
| [21] | Trefethen,L.Spectral Methods in Matlab,Tsinghua University Press,Beijing(2011) |
| [22] | Schmid,P.J.and Henningson,D.S.Optimal energy density growth in Hagen-Poiseuille flow. Journal of Fluid Mechanics,277,197-225(1994) |
| [23] | Meseguer,A.and Mellibovsky,F.On a solenoidal Fourier-Chebyshev spectral method for stability analysis of the Hagen-Poiseuille flow. Applied Numerical Mathematics,57,920-938(2007) |
| [24] | Zagarola,M.V.and Smits,A.J.Mean-flow scaling of turbulent pipe flow. Journal of Fluid Mechanics,373,33-79(1998) |
| [25] | Deng,B.Q.,Xu,C.X.,Huang,W.X.,and Cui,G.X.,Effect of active control on optimal structures in wall turbulence.Science China Physics,Mechanics and Astronomy,56,290-297(2013) |
| [26] | Bailey,S.C.C.and Smits,A.J.Experimental investigation of the structure of large- and verylarge- scale motions in turbulent pipe flow.Journal of Fluid Mechanics,651,339-356(2010) |
 2015,Vol.36
2015,Vol.36




















