Shanghai University
Article Information
- R. TRÎMBIŢAŞ, T. GROSAN, I. POP. 2015.
- Mixed convection boundary layer flow past vertical flat plate in nanofluid: case of prescribed wall heat flux
- Appl. Math. Mech. -Engl. Ed., 36(8): 1091-1104
- http://dx.doi.org/10.1007/s10483-015-1967-7
Article History
- Received Jan. 12, 2015;
- in final form May 22, 2015
1 Introduction
Convective flow occurs in nature,science,and engineering which is important from theoretical as well as practical points of view because of its wide applications in polymer technology and metallurgy. Fluid heating and cooling are important in many industrial and engineering applications,such as aerodynamic extrusion of plastic sheet,the cooling of metallic plate in a cooling bath,and in thin film solar energy collector device,solar receivers exposed to wind currents,electronic devices cooled by fans,nuclear reactors cooled during emergency shutdown, heat exchanges placed in a low-velocity environment,flows in the ocean and in the atmosphere, etc. A comprehensive review of buoyancy induced flows is given in the books of Gebhart et al. [1] ,Schlichting and Gersten [2],Pop and Ingham [3] ,andBejan [4] .
The free and mixed convection boundary layer flow past a vertical flat plate is a classical problem and has been studied by many investigators. Wilks [5] studied the uniform stream over a semi-infinite vertical flat plate with uniform surface heat flux. Merkin [6] considered the solution of the free convection on a heated vertical plate for a small Prandtl number. Also, Merkin and Mahmood[7] considered the free convection boundary layer on a vertical plate with a prescribed surface heat flux proportional to (1 +x2)μ (μ is a constant),while Merkin and Mahmood[8] ,and Ghosh and Yao [9] analyzed the mixed convection along a semi-infinite vertical flat plate with uniform surface heat flux.
Most of the studies on convective flow of Newtonian fluids have used the base fluid with a low thermal conductivity,which,in turn,limits the heat transfer enhancement. An innovative technique to enhance heat transfer is by using nano-scale particles in the base fluid. Nanotechnology has been widely used in industry since materials with sizes of nanometers possess unique physical and chemical properties. Nano-scale particle added fluids are called nanofluids (see Choi [10] ) and show promise in significantly increasing heat transfer rates in a variety of applications. Nanotechnology has been widely used in industry since materials with sizes of nanometers possess unique physical and chemical properties. It represents the most relevant technological cutting edge currently being explored. Some numerical and experimental studies on nanofluids include thermal conductivity (see Khanafer et al. [11] ,Ding et al. [12] ,Tiwariand Das[13] ,Oztop and Abu-Nada [14] ,etc.). A very interesting critical synthesis of the variants within the thermophysical properties of nanofluids has been recently presented by Khanafer and Vafai [15] . This study shows that it is not clear which analytical model should be used to describe the thermal conductivity of nanofluids. Additional theoretical and experimental research studies are required to clarify the mechanisms responsible for heat transfer enhancement in nanofluids. In recent years,many researchers have investigated the effects of nanofluids on the enhancement of heat transfer in thermal engineering devices,both experimentally and theoretically and the number of publications related to nanofluids increases in an exponential manner. A series of papers [16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27] have considered the boundary layer flow and heat transfer past different kinds of geometries in a water based nanofluid. The broad range of current and future applications of nanofluids is discussed in the book of Das et al. [28] and in the review papers of Kaka¸cand Pramuanjaroenkij [29] ,Wong and Leon [30] ,Saidur et al. [31] ,Mahian et al. [32] ,etc. The paper by Wong and Leon[30] included automotive,electronics,biomedical,and heat transfer applications besides other applications such as nanofluid detergent. Saidur et al. [31] presented some applications of nanofluids in industrial,commercial,residential,and transportation sectors based on available literatures. The capability of nanofluids to enhance thermal conductivity has attracted the interest of fluid dynamics community to conduct further studies.
The principal aim of the present investigation is to extend the problem considered by Merkin and Mahmood [8] on the mixed convection boundary layer similarity solutions: prescribed wall heat flux to the case when the cylinder is placed in a water-based nanofluid. The study has been motivated by the need to determine the thermal performance of such a system. The problem is formulated for general types of nanoparticles water as a base fluid. By using a similarity transformation,these coupled and non-linear partial differential equations are transformed into coupled non-linear ordinary differential equations. Owing to the highly non-linear equations of state for nanofluids,the resulting governing equations are much complex in nature and therefore, numerical solutions are sought using the bvp4c function from MATLAB [36, 37] . For the case of regular fluid (φ= 0),the results are validated with previously published papers. Based on the above literature survey and to the best authors’ knowledge,no previous study on Merkin and Mahmood’s[8] problem in nanofluid has been studied yet.
2 Basicequations
We consider the mixed steady convection boundary layer flow past a vertical flat plate placed
in a nanofluid as shown in Fig. 1,where 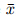 and
and 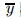 are the Cartesian coordinates measured along
and normal to the plate,respectively. It is assumed that the mainstream velocity is
are the Cartesian coordinates measured along
and normal to the plate,respectively. It is assumed that the mainstream velocity is  ,and
the temperature of the ambient nanofluid is T∞,while the prescribed wall heat flux is
,and
the temperature of the ambient nanofluid is T∞,while the prescribed wall heat flux is  ,
where
,
where 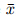 is the coordinate measured along the plate in the upward direction. Under these assumptions,using the model of the nanofluid proposed by Tiwari and Das
[13]
,the equations
governing this problem
[8]
are
is the coordinate measured along the plate in the upward direction. Under these assumptions,using the model of the nanofluid proposed by Tiwari and Das
[13]
,the equations
governing this problem
[8]
are
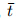 is the time,
is the time,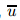 and
and 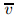 are the velocity components along the
are the velocity components along the 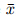 and
and 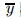 directions,
directions,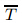 is the
temperature of the nanofluid,g is the acceleration due to gravity,φ is the nanoparticle volume
fraction,l is a characteristic length of the plate,q<0 is the constant characteristic of the heat
flux with q<0>0 for a heated plate(assisting flow)and q<0<0 for a cooled plate (opposing
flow),respectively,U<0 is a constant velocity characteristic,m< is a positive number and β is the
coefficient of volume expansion. Further,μnf is the dynamic viscosity of the nanofluid,αnf is
the thermal diffusivity of the nanofluid,and knf is the thermal conductivity of the nanofluid,whicharegivenby(OztopandAbuNada
[14]
),
is the
temperature of the nanofluid,g is the acceleration due to gravity,φ is the nanoparticle volume
fraction,l is a characteristic length of the plate,q<0 is the constant characteristic of the heat
flux with q<0>0 for a heated plate(assisting flow)and q<0<0 for a cooled plate (opposing
flow),respectively,U<0 is a constant velocity characteristic,m< is a positive number and β is the
coefficient of volume expansion. Further,μnf is the dynamic viscosity of the nanofluid,αnf is
the thermal diffusivity of the nanofluid,and knf is the thermal conductivity of the nanofluid,whicharegivenby(OztopandAbuNada
[14]
),
 |
| Fig. 1 Physical model and coordinate system |
where (ρCp)nf is the heat capacitance of the nanofluid. The dynamic viscosity of the nanofluid μnfcan be approximated as the viscosity of a base fluid μf containing dilute suspension of fine spherical particles and is given by Brinkman [33] . The subscripts f and s refer to the fluid and solid fractions,respectively. It is worth mentioning that the expressions (5) are restricted to spherical nanoparticles where it does not account for other shapes of nanoparticles.
We introduce now the following dimensionless variables:
where Re=U0l/νf is the Reynolds number. Substituting (6) into (1)-(3),we get and the initial and boundary conditions (4) become Here,Pr=νf/αf is the Prandtl number,and λ is the constant mixed convection parameter, which is defined as where Gr=gβf(q0/k)(vl/U0) 1/2(l3/ν2f) is the Grashof number. It should be noted that λ>0 corresponds to a heated plate (assisting flow),and λ<0 corresponds to a cooled plate (opposing flow),respectively.The physical quantities of interest are the skin friction coefficient Cf and the Nusselt number Nu,which are defined as
Using (6) and (12),we obtain3 Steadyflowcase
In this case = 0,following Merkin and Mahmood[8]
,we look for similarity solutions of
(7)-(9) subject to the boundary conditions (10) of the following form:
= 0,following Merkin and Mahmood[8]
,we look for similarity solutions of
(7)-(9) subject to the boundary conditions (10) of the following form:
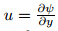 and
and 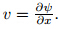 .
Substituting (6) into (2) and (3),we obtain the following ordinary differential equations:
and the boundary conditions (4) become
Here,primes denote differentiation with respect to η. Inthiscase,theskinfrictioncoefficient
Cf and the local Nusselt number Nux are given by,from (13),
where Rex=ue(x)x/νf is the local Reynolds number. It is worth mentioning to this end that
the present study reduces to that of Merkin and Mahmood
[8]
for a viscous fluid when φ=0
(regular fluid).
.
Substituting (6) into (2) and (3),we obtain the following ordinary differential equations:
and the boundary conditions (4) become
Here,primes denote differentiation with respect to η. Inthiscase,theskinfrictioncoefficient
Cf and the local Nusselt number Nux are given by,from (13),
where Rex=ue(x)x/νf is the local Reynolds number. It is worth mentioning to this end that
the present study reduces to that of Merkin and Mahmood
[8]
for a viscous fluid when φ=0
(regular fluid).Further,for λ>>1,we introduce the following new variables:
Thus,(15) and (16) become and the boundary conditions (4) become Thus,the values of f"(0) and θ(0) are given by For a viscous fluid (φ= 0),(20) and (21) reduce to with the boundary conditions which are (7) with the boundary conditions (8) from the paper of Merkin and Mahmood [8] .4 Stability analysis
Weidman et al.[34] and Ro¸sca and Pop [35] have shown for the forced convection boundary layer flow past a permeable flat plate,for the forced convection flow of a non-Newtonian fluid past a wedge and for the flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second-order slip,that the lower branch solutions are unstable (not realizable physically),while the upper branch solutions are stable (physically realizable). We test these features by considering the unsteady boundary layer equations (7) to (9) with the boundary conditions (10). Thus,we introduce the dimensionless variables:
The use of τ is associated with an initial value problem and is consistent with the question of which solution will be obtained in practice (physically realizable). Using the variables (27),(8) and (9) can be written as subject to the boundary conditions To test stability of the steady flow solution f(η)=f0(η) and θ(η)=θ0(η) satisfying the boundaryvalue problem (15) and (16),we write (see Weidman et al. [34] or Ro¸sca and Pop [35] ), where γ is an unknown eigenvalue parameter,and F(η,τ) and G(η,τ) are small relative to f0(η) and θ0(η). Substituting (1) into (28) and (29),we obtain the following linearized problem: along with the boundary conditions As suggested by Weidman et al.[34] ,we investigate the stability of the steady flow and heat transfer solution f0(η) and θ0(η) by setting τ= 0,and hence F=F0(η) and G= G0(η) in (32) and (33) to identify initial growth or order decay of the solution (31). Thus,we have to solve the corresponding linear eigenvalue problem along with the boundary conditions It should be mentioned that for particular values of λ,φ,m,and Pr the corresponding steady flow solution f0(η) and θ0(η)(either the physical or the dual solution),the stability of the steady flow solution is determined by the smallest eigenvalue γ. From (31) it follows that for γ>0 the flow is stable,while for γ<0 the perturbation is magnified and,therefore,the solution of the problem (15) to (17) is unstable. The range of possible eigenvalues can be investigated by discretizing the derivatives from (35) and (36) using MATLAB chebfun (see Driscoll et al. [38]) and solving the generalized eigenvalue problem.5 Results and discussion
Numerical solutions to the governing ordinary differential equations (15)-(16) and (20)- (21) with the boundary conditions (17) and (22) were obtained for several values of the mixed convection parameter λ and nanoparticle volume fraction φ with m= 1 (stagnation point flow) and m=3/5 (constant heat flux),respectively,using the bvp4c function from MATLAB [36, 37] . Because the physical domain is unbounded,whereas the computational domain has to be finite, we apply the far field boundary conditions for the similarity variable η at a finite value denoted here by η=ηmax. In order to achieve the asymptotic limit,we use in the computations different values of ηmax (in the range 20 to 50) which depend on the considered governing parameters. Following Khanafer et al. [11] and Oztop and Abu-Nada [14] the value of the Prandtl numberPr is taken as 6.2 (water),and the volume fraction of nanoparticles is from 0 to 0.2 (0≤φ≤0.2) in which φ= 0 corresponds to the regular (Newtonian) fluid. The thermophysical properties of the base fluid and the nanoparticles are listed in Table 1.
 |
Comparison of the reduced skin friction f"(0) and dimensionless wall temperature θ(0) for m= 1 (stagnation point flow),m=3/5 (constant heat flux) when Pr=1,φ= 0 (regular fluid) and λ≥1 (free convection) with those reported by Merkin and Mahmood [8] isgivenin Table 2. It is seen that these results are in very goodagreement,we are convinced that the present numerical results are correct and very accurate.
 |
Solving equations (15) and (16) with the boundary conditions (17) shows that dual solutions exist for the case of opposing flow (λ<0). The variations off"(0) and θ(0) with λ are shown in Figs. 2 to 4 for some values of the nanoparticle volume fraction φwith Cu-water working fluid. These figures show that there are regions of unique solutions for λ≥0,dual (upper and lower branches) solutions for λc ≤λ<0 and no solutions for λ<λc<0,where λc is the critical value of λ(<0). However,for λ<λc<0 the problem has to be studied using the full Navier-Stokes and energy equations. Based on the present computation,it is found that for m=1 and Pr= 1 the value of λc is −1.193 61 which is in agreement with those reported by Merkin and Mahmood [8] for a regular fluid (φ= 0) (see Table 3). In addition, the behaviour of the first and second solution for m=1 and 3/5 and Pr= 1 is similar with that reported in Ref. [8] (see Fig. 4). Further,it should be mentioned that the stability analysis results demonstrate that the upper branch solutions are stable and physically realizable,while the lower branch solutions are unstable and,therefore,not physically realizable. The smallest eigenvaluesγrelated to the stability problem (35) to (37) at several values of λ(<0,opposing flow) for Pr=6.2,m=3/5 and 1,and different values of φare presented in Table 4.
 |
| Fig. 2 Variation of f"(0) and θ(0) with λ for Pr=6.2,m= 1,and several values of φ |
 |
| Fig. 3 Variation of f"(0) and θ(0) with λ for Pr=6.2,m=3/5 and several values of φ(see Merkin and Mahmood [8] ) |
 |
| Fig. 4 Variation of f"(0) and θ(0) with λ for Pr=1,m=1,and m=3/5 when φ=0(see Merkin and Mahmood [8] ) |
 |
The velocity and temperature profiles are presented in Figs. 5 to 8 for some values of the governing parameters. Figures 5 and 6 illustrate the stable and unstable velocity and temperature profiles for several values of φand m=1 and 3/5,when λ=−2 and λ=−1,respectively (opposing flow). The thicknesses of the boundary layers are higher for the second (unstable) than for the first (stable) solution. In addition,for the stable solution,temperature and velocity boundary layer thicknesses decrease with the increase of nanoparticles volume fraction parameter φ. Further,a reverse flow is noticed from Figs. 5a and 6a in the case of unstable solution. It should be noted that for the unstable solution temperature and velocity boundary layer thicknesses increase with the increase of nanoparticles volume fraction parameter φ. Moreover,the thicknesses of the boundary layer for both velocity and temperature profiles are higher for the lower branch solution which is in agreement with the results obtained by stability analysis. Finally,Figs. 7 and 8 present the velocity and temperature profiles for m=1 and m=3/5,and several values of φ when λ= 50 (assisting flow). Due to the large value of λ an overshoot of the velocity profile is observed (see Fig. 7(a) and 8(a)). This is in agreement with the physical phenomenon that for large values of λ the convective heat transfer dominates the conductive heat transfer. In addition it is seen that the dimensionless wall temperature decreases with the increasing of nanoparticle volume fraction parameter φ.
 |
| Fig. 5 Stable and unstable velocity f' (η) and temperature θ(η)profilesfor m= 1 and several values of φ when λ=−2 |
 |
| Fig. 6 Stable and unstable velocity f' (η) and temperature θ(η)profilesfor m=3/5 and several values of φ when λ=−1 |
 |
| Fig. 7 Velocity f'(η) and temperature θ(η)profiles for λ= 50 and several values of φ when m=1 |
 |
| Fig. 8 Velocityf'(η) and temperature θ(η) profiles for λ= 50 and several values of φ when m=3/5 |
6 Conclusions
We present an analysis for the mixed convection boundary layer flow and heat transfer characteristics of a Cu-water nanofluid over a semi-infinite vertical flat plate considering a given heat flux on the wall. The study reveals that the range of the mixed convection parameter λ, where the similarity solution exists,is larger for an assisting flow compared with the opposing flow case. Different from the assisting flow case,it is found that the solutions for an opposing flow are non-unique. The inclusion of nanoparticles into the water based fluid produces an increase in the skin friction and heat transfer coefficients.
Acknowledgement The authors would like to express their thanks to the very competent reviewers for the very good comments and suggestions.
| [1] | Gebhart, B., Jaluria, Y., Mahajan, R. L., and Sammakia, B. Buoyancy-Induced Flows and Transport, Hemisphere, New York (1988) |
| [2] | Schlichting, H. and Gersten, K. Boundary Layer Theory, Springer, New York (2003) |
| [3] | Pop, I. and Ingham, D. B. Convective Heat Transfer:Mathematical and Computational Viscous Fluids and Porous Media, Pergamon, Oxford (2001) |
| [4] | Bejan, A. Convection Heat Transfer, Wiley, New Jersey (2013) |
| [5] | Wilks, G. The flow of a uniform stream over a semi-infinite vertical flat plate with uniform surface heat flux. International Journal of Heat and Mass Transfer, 17, 743-753(1974) |
| [6] | Merkin, J. H. Free convection on a heated vertical plate:the solution for small Prandtl number. Journal of Engineering Mathematics, 23, 273-282(1989) |
| [7] | Merkin, J. H. and Mahmood, T. On the free convection boundary layer on a vertical plate with prescribed surface heat flux. Journal of Engineering Mathematics, 24, 95-107(1990) |
| [8] | Merkin, J. H. and Mahmood, T. Mixed convection boundary layer similarity solutions:prescribed wall heat flux. Journal of Applied Mathematics and Physics (ZAMP), 40, 51-68(1989) |
| [9] | Ghosh, M. S. and Yao, L. S. Mixed convection along a semi-infinite vertical flat plate with uniform surface heat flux. ASME Journal of Heat Transfer, 131, 022502-1-022502-8(2009) |
| [10] | Choi, S. U. S. Enhancing thermal conductivity of fluids with nanoparticles. ASME Fluids Engineering Division, 231, 99-105(1995) |
| [11] | Khanafer, K., Vafai, K., and Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. International Journal of Heat and Mass Transfer, 46, 3639-3653(2003) |
| [12] | Ding, Y., Chen, H., Wang, L., Yang, C. Y., He, Y., Yang, W., Lee, W. P., Zhang, L., and Huo, R. Heat transfer intensification using nanofluids. Kona, 25, 23-38(2007) |
| [13] | Tiwari, R. K. and Das, M. K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. International Journal of Heat and Mass Transfer, 50, 2002-2018(2007) |
| [14] | Oztop, H. F. and Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. International Journal of Heat and Fluid Flow, 29, 1326-1336(2008) |
| [15] | Khanafer, K. and Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. International Journal of Heat and Mass Transfer, 54, 4410-4428(2011) |
| [16] | Ahmad, S. and Pop, I. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids. International Communications in Heat and Mass Transfer, 37, 987-991(2010) |
| [17] | Ahmad, S., Rohni, A. M., and Pop, I. Blasius and Sakiadis problems in nanofluids. Acta Mechanica, 218, 195-204(2011) |
| [18] | Rohni, A. M., Ahmad, S., and Pop, I. Boundary layer flow over a moving surface in a nanofluid beneath a uniform free stream. International Journal of Numerical Methods for Heat & Fluid Flow, 21, 828-846(2011) |
| [19] | Rohni, A. M., Ahmad, S., and Pop, I. Flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids. International Journal of Heat and Mass Transfer, 55, 1888-1895(2012) |
| [20] | Rohni, A. M., Ahmad, S., Merkin, J. H., and Pop, I. Mixed convection boundary layer flow along a vertical cylinder embedded in a porous medium filled by a nanofluid. Transport Porous Media, 96, 237-253(2013) |
| [21] | Jashim, U. M., Pop, I., and Ismail, M. A. I. Free convection boundary layer flow of a nanofluid from a convectively heated vertical plate with linear momentum slip boundary condition. Sains Malaysiana, 41, 1475-1482(2012) |
| [22] | Rosca, A. V., Rosca, N. C., Grosan, T., and Pop, I. Non-Darcy mixed convection from a horizontal plate embedded in a nanofluid saturated porous media. International Communications in Heat and Mass Transfer, 39, 1080-1085(2012) |
| [23] | Natalia, C., Rosca, T. G. and Pop, I. Stagnation-point flow and mass transfer with chemical reaction past a permeable stretching/shrinking sheet in a nanofluid. Sains Malaysiana, 41, 1271-1279(2012) |
| [24] | Bachok, N., Ishak, A., Nazar, R., and Pop, I. Flow and heat transfer at a general three-dimensional stagnation point in a nanofluid. Physica B, 405, 4914-4918(2010) |
| [25] | Bachok, N., Ishak, A., and Pop, I. Flow and heat transfer characteristics on a moving plate in a nanofluid. International Journal of Heat and Mass Transfer, 55, 642-648(2012) |
| [26] | Trimbitas, R., Grosan, T., and Pop, I. Mixed convection boundary layer flow along vertical thin needles in nanofluids. International Journal of Numerical Methods for Heat & Fluid Flow, 24, 579-594(2014) |
| [27] | Patrulescu, F. O., Grosan, T., and Pop, I. Mixed convection boundary layer flow from a vertical truncated cone in a nanofluid. International Journal of Numerical Methods for Heat & Fluid Flow, 24, 1175-1190(2014) |
| [28] | Das, S. K., Choi, S. U. S., Yu, W., and Pradet, T. Nanofluids:Science and Technology, Wiley, New Jersey (2007) |
| [29] | Kakaç, S. and Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. International Journal of Heat and Mass Transfer, 52, 3187-3196(2009) |
| [30] | Wong, K. F. V. and Leon, O. D. Applications of nanofluids:current and future. Advances in Mechanical Engineering, 519659(2010) |
| [31] | Saidur, R., Kazi, S. N., Hossain, M. S., Rahman, M. M., and Mohammed, H. A. A review on the performance of nanoparticles suspended with refrigerants and lubricating oils in refrigeration systems. Renewable and Sustainable Energy Reviews, 15, 310-323(2011) |
| [32] | Mahian, O., Kianifar, A., Kalogirou, S. A., Pop, I., and Wongwises, S. A review of the applications of nanofluids in solar energy. International Journal of Heat and Mass Transfer, 57, 582-594(2013) |
| [33] | Brinkman, H. C. The viscosity of concentrated suspensions and solutions. Journal of Chemical Physics, 20, 571-581(1952) |
| [34] | Weidman, P. D., Kubitschek, D. G., and Davis, A. M. J. The effect of transpiration on selfsimilar boundary layer flow over moving surface. International Journal of Engineering Science, 44, 730-737(2006) |
| [35] | Rosca, A. V. and Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. International Journal of Heat and Mass Transfer, 60, 355-364(2013) |
| [36] | Shampine, L. F., Gladwell, I., and Thompson, S. Solving ODEs with MATLAB, Cambridge University Press, Cambridge (2003) |
| [37] | Shampine, L. F., Reichelt, M. W., and Kierzenka, J. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. http://www.mathworks.com/bvp_tutorial |
| [38] | Driscoll, T. A., Hale, N., and Trefethen, L. N. Chebfun Guide, Pafnuty Publications, Oxford (2014) |
 2015, Vol. 36
2015, Vol. 36








































