Shanghai University
Article Information
- Benwen LI,Shangshang CHEN.2015.
- Direct spectral domain decomposition method for 2D incompressible Navier-Stokes equations
- Appl.Math.Mech.-Engl.Ed.,36(8): 1073-1090
- http://dx.doi.org/10.1007/s10483-015-1964-7
Article History
- Received Dec. 24, 2014;
- in final form May 22, 2015
2.Key Laboratory of Electromagnetic Processing of Materials(Ministry of Education),Northeastern University,Shenyang 110819,China
1 Introduction
In the past decades,spectral methods have been sufficiently developed and used in computational fluid dynamics(CFD)due to the exponential convergence.Traditionally,the computational domains are usually defined in rectangular or circular regions in which cases Chebyshev or Fourier expansions,respectively,are appropriate.However,the application of spectral methods to solve the fluid flow in complex geometries is difficult.In order to extend the scope of the spectral methods’ application,the domain decomposition concept is adopted to help the methods to handle the complex geometry problems where the computational domain can be decomposed into several rectangular sub-domains.Canuto et al.[1] and Peyret[2] have given a comprehensive review about the spectral domain decomposition methods(multi-domain spectral method),including the patching methods [3] ,overlapping methods [4] ,and spectral element methods[5,6,7] .
Early in 1987,Zanolli [8] proposed an iterative multi-domain method which can reduce the given problem to a sequence of mixed boundary value problem in each sub-domain by importing the relaxation parameter.Funaro et al. [9] used the method to study the second-order elliptic problems.Furthermore,Louchart et al. [10,11] extended the method to solve the 2D incompressible Navier-Stokes equations in primitive variable formulation.Instead of solving Dirichlet and Neumann boundary conditions alternatively on sub-domains during the same internal,the continuity of variables were first satisfied by the relaxation parameter and followed by the Neumann condition for the normal derivatives.In addition,Pinelli and Vacca [12] used the iterative method and pseudo-spectral Chebyshev expansion method to investigate the 2D flow in an asymmetric channel after the application of the projection algorithm.Without any doubt,compared with the iterative algorithm,the direct domain decomposition methods always have more attraction.For this purpose,a direct spectral domain decomposition method based on the influence matrix technique[12,13] was developed for the 2D incompressible flows by using the vorticity-streamfunction formulation [14,15,16,17,18] .Also,the influence matrix technique was used to treat the lack of vorticity boundary conditions on no-slip walls as well as to enforce the continuity conditions at theinterfaces between adjacent sub-domains.For instance,Raspo [18] investigated the Navier-Stokes equations in vorticity-streamfunction formulation with the direct multi-domain technique for the rotating flows in T-shape geometry,and accurate numerical results wereobtained.But in theory,the extension of the method based on vorticity-streamfunction formulation to 3D flows seems difficult to be carried out and the pressure fields are usually unknown.Therefore,the direct domain decomposition methods for the Navier-Stokes equations in velocity-pressure variables were emerged as the required.Danabasoglu et al. [19] studied channel flows using a mixed collocation spectral/finite difference method. Sabbah and Pasquetti [20] developed another direct multi-domain method based on the influence matrix technique for the solution of the Navier-Stokes equations in velocity-pressure variables, and the Rayleigh-B´enard convection in 2D and 3D cavitiesof large aspect ratio was considered. The “extended influence matrix” method was implemented for computation of the pressure and correction term at the physical boundary and the correction term were introduced into the solution to the Poisson equation for pressure in order to recover the divergence-free velocity field at the boundary of the computational domain.Furthermore,Droll and Sch¨ afer [21] presented an implicit pseudospectral method allowing an efficient prediction of incompressible flows in moderately complex geometries.The method based on a Chebyshev collocation discretization in a multi-domain setting with an iterative solver,whose efficiency was based on a precondition employing ideas from a direct Helmholtz solver.In addition,we have reviewed some more recent studies of spectral domain decomposition as well,these studies include radiation transfer problem [22],the electromagnetic plasma problem [23] ,the biological flow [24] ,theseismicwave propagation [25] ,Burger’s-Fisher [26] and Schr¨odinger equations [27] ,etc.According to our knowledge,it is still a very meaningful task to develop a new accurate and simple spectral domain decomposition algorithm to deal with the fluid flows in the complex geometries.And it can be foreseen that the spectral domain decomposition method will play a more important role to accurate and efficiently simulate the fluid flows in complex geometries,especially to solve the multi-physical coupling problems,like the magnetohydrodynamics(MHD) [28,29,30,31] and the radiation magnetohydrodynamics(RMHD) [32] ,in the future works.
In the present work,we present a direct spectral domain decomposition method for the
solution of the incompressible Navier-Stokes equations in primitive variable formulation.The
coupling of the velocity and the pressure is solved by an efficient improved projection scheme
[33]
,which makes sure of a divergence-free velocityfield at each time step.The Chebyshev collocation spectral method(CSM)is used for spatial approximation,and a combination of AdamsBashforth and the backward difference formula(AB/BDF)scheme,which has the second order
accuracy,is adopted for the time integration.Thus at each time step,we just have to solve
Helmholtz equations(u and v)with Dirichlet boundary conditions and Poisson equations(p
and )with Neumann boundary conditions,respectively.The influence matrix technique is
used to enforce the continuities of both variables and their normal derivative between adjacent
sub-domains.The aim of this method is to obtain the accurate values of velocity and pressure
at each time step in a direct way.
)with Neumann boundary conditions,respectively.The influence matrix technique is
used to enforce the continuities of both variables and their normal derivative between adjacent
sub-domains.The aim of this method is to obtain the accurate values of velocity and pressure
at each time step in a direct way.
Three test cases are considered to validate effectiveness and applicability of the present method.Firstly,the analytical solutions defined in the inverted L-shape domain are considered to assess the accuracy and stability of the method.Secondly,the Lid-driven cavity flow in a square cavity is discussed,and the results are compared with available solutions in the literature. Finally,the regularized driven cavity flow in the inverted L-shape geometry is solved,and the flow streamlines are given against the Reynolds number.
2 Formulation
2.1 Governing equations
We consider the unsteady incompressible Navier-Stokes equations in a dimensionless form,
where Re is the Reynolds number,V andpare the dimensionless velocity vector and pressure, Fis the body force.These equations are solved with the given boundary and initial conditions below 3 Solution procedure3.1 Temporal scheme
A combination of the Adams-Bashforth and backward difference formula(AB/BDF)schemes, which can ensure the good stability,is used for the time integration.The resulting scheme is semi-implicit,and for(1),
whereN(V)represents the nonlinear term.For the initial step,we take V −1=V0. 3.2 Improved projection scheme(IPS)The improved projection scheme is used to deal with the coupling of the velocity and pressure.The detailed process can be found in Ref.[33].
(1)Solve the preliminary pressure 
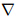 ×(
×(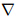 ×V).
×V).(2)Solve the prediction velocity V*
with the actual Dirichlet boundary condition(3)Solve intermediate variable
with the consistent Neumann boundary condition(4)The correct velocity and pressure in
 =Ω∪Γ are
=Ω∪Γ are
For the spatial approximation,the Chebyshev-Gauss-Lobatto(CGL)collocation points are implemented.
To meet the requirement of the CGL collocation points,the arbitrary intervals [x1,x2]× [y1,y2] should be mapped into the standard intervals [−1,1]×[−1,1].For the domain decomposition method,the coordinate transformation is carried out locally in each sub-domain in both x- and y-directions,respectively.The coordinate transformations are
Using the Lagrange interpolation polynomial,the variable of Navier-Stokes equations f (stands for u,v,and p)can be approximated on collocation points,like
Substituting(15)into(6),the discretization of Poisson equation can be written in a matrix form,
where the element expressions of matrices A,B,and C are with 
The discretizations of the momentum equation(8)and the intermediate variable equation (10)are similar to that of the pressure equation(6).
3.4 Direct domain decomposition method
In the former studies,the applications of the direct spectral domain decomposition method
based on the influence matrix technique to the Poisson equations of preliminary pressure ¯ p
n+1
and intermediate variable  have shown limitations of satisfying the continuity of the first-order
normal derivative on the interface.The problem comes from the introduction of the Neumann
boundary conditions to Poisson equations,and this can lead to indeterminate solution.We
successfully overcome this obstacle by assuming the Dirichlet boundary conditions on interface,
and using the first-order normal derivatives as transmission conditions to keep the continuities
of variables.We describe the domain decomposition approach for(6)in the inverted L-shape
geometry(see Fig.1),which is decomposed into three sub-domains with interfaces γ12and γ23.
have shown limitations of satisfying the continuity of the first-order
normal derivative on the interface.The problem comes from the introduction of the Neumann
boundary conditions to Poisson equations,and this can lead to indeterminate solution.We
successfully overcome this obstacle by assuming the Dirichlet boundary conditions on interface,
and using the first-order normal derivatives as transmission conditions to keep the continuities
of variables.We describe the domain decomposition approach for(6)in the inverted L-shape
geometry(see Fig.1),which is decomposed into three sub-domains with interfaces γ12and γ23.
 |
| Fig.1 Domain decomposition for inverted L-shape geometry |
Along the interfaces γ12and γ23,we enforce the continuity of the solution and its first normal derivative.We apply
Mathematically,by using the principle of superposition,the solution  in each sub-domain
is written as
in each sub-domain
is written as
For the reason of simplification,we just restrict our consideration to  in the sub-domain
Ω2.More precisely,the elementary solutions
in the sub-domain
Ω2.More precisely,the elementary solutions  satisfy the following discrete
problems in a matrix form:
satisfy the following discrete
problems in a matrix form:
Once all the algebraic systems in three sub-domains such as(22)-(24)are solved,they will be substituted into(20)-(21)to make the solution continuous
In a matrix form,
where ξ=(ξ12,ξ23) T ,and M is the influence matrix.However,the matrix M is found to have one null eigenvalue.For incompressible flows,this null eigenvalue has the physical meaning, which is associated with a constant pressure field.Thus,we can replace the matrix M with a matrix M0 in which the null eigenvalue is replaced by any nonzero value σ [34].In the present study,we set σ= 1.Then,M0 can be inverted,and the values ξ can be determined byAfter the determination of ξ,the solutions of  in three sub-domains can be calculated
independently by(22)-(24).
in three sub-domains can be calculated
independently by(22)-(24).
In summary,the  is replaced by the three algebraic problems
is replaced by the three algebraic problems  with
mixed boundary conditions.For the unsteady Navier-Stokes equations,
with
mixed boundary conditions.For the unsteady Navier-Stokes equations, is solved at each
time step,but the
is solved at each
time step,but the  and
and  only need to be solved once before the time integration.Hence,
the influence matrix M0 and its inverse also only need to be calculated once for all.
only need to be solved once before the time integration.Hence,
the influence matrix M0 and its inverse also only need to be calculated once for all.
3.5 Solution procedure
The implementation of the spectral domain decomposition for solving the Navier-Stokes equations in the inverted L-shape geometry can be carried out through the following routines:
(i)Decompose the computational domain into three rectangular sub-domains.Set the number of collocation points Nx and Ny in each sub-domain.
(ii)Choose the time step to satisfy the Courant-Friedrichs-Lewy(CFL)condition.Compute the coefficient matrices A,B and the influence matrices of the preliminary pressure,prediction velocity,and intermediate variable.
(iii)Give the initial velocity field and start to the time integration.
(iv)Calculate the right-hand side matrix C of the preliminary pressure in each sub-domain.
Impose the boundary condition(7),then solve the algebraic problems  and calculate E.
and calculate E.
(v)Calculate the true interface values of the preliminary pressure ξ by(28).Then get the
solution of  in each sub-domain.
in each sub-domain.
(vi)Do the similar process as in Step 4 and Step 5 for prediction velocity and intermediate
variable in each sub-domain.Then get the solutions of um,vm,and  in each sub-domain.
in each sub-domain.
(vii)Correct velocity and pressure fields by(12).
(viii)If up to finial time,then terminate the time integration and go to step 9.Otherwise, go back to Step 4 using new velocity and pressure instead of the previous velocity and pressure.
(ix)Output the result.
In the above procedure,all the matrix equations are solved efficiently by the two-step direct solver [35] .The computations of eigenvectors,eigenvalues,and their inverses of corresponding matrices are finished once in all in the preprocessing step before starting the time integration. Thereafter,at each time step the solutions are obtained from simple matrix products.Moreover, the solution procedures of the Navier-Stokes equations in more complex geometries are similar to those of the inverted L-shape geometry.
4 Results and discussion
4.1 Analytical solutions of transient Navier-Stokes equations
The analytical solutions [34] which are defined in the inverted L-shape domain(see Fig.1)are used for the spatial accuracy checking and temporal convergence studying.The exact solutions are
with an analytical source term F where α= 10,β=5,and Re= 100.We use the L2and L∞ errors [36] to evaluate the accuracy of present method.Their expres-sions are as follows:
wheref(xi,yj,t)is the exact solutions,and fNx,Ny (xi,yj,t) is the computed one.Because the pressure appears only in the way of gradient,the errors of the first-order derivative along the x direction are taken as the measurement of the accuracy of pressure field.
The computational domain is decomposed into three rectangular sub-domains with two
interface lines γ12 and γ23.The spatial resolutions of Nx×Ny =8×8 to 36×36 with the
increment of 4×4ineachsub-domainareusedandthetimestepisfixedatΔt=10−4
,which
meets the CFL condition[36]
and the finial time is T= 2.As shown in Fig.2,the convergence
rate of the CSM is very fast and approximately follows an exponential law.However,the
spatial errors will not decrease continuously with the collocation points and they are frozen at
some level,because the temporal scheme used here is just second-order accurate.For the time
accuracy,the results are given in Fig.3,it canbe seen that a full second-order accuracy can be
achieved for u,v,and ∂xp in each sub-domain.The time histories of the divergence errors are
shown in Fig.4,and they depict the ability of the method to accurately enforce  ·V=0in
long time simulations.
·V=0in
long time simulations.
 |
| Fig.2 L2 errors at T=2 for u,v,and ∂xp against spatial resolution in three sub-domains(Re=100,Δt=10−4 ) |
 |
| Fig.3 L2 errors at T =2 for u,v,and ∂xp against time step in three sub-domains(Re=100, Nx×Ny=36×36) |
 |
| Fig.4 L∞< errors for divergence against time in three sub-domains(Re=100,Nx×Ny=36×36, and Δt=10−3 ) |
4.2 Lid-driven cavity flow in square cavity
Lid-driven cavity flow in a square cavity is one of the most classic problems in the field of CFD.Beginning from Burggraf [37] ,many researchers [38,39,40] have investigated this problem and given the classical numerical solutions.The computational domain is(0,1)×(0,1).The driven speed of top wall is V|y=1=(1,0),and the zero-slip condition is imposed to the other walls. With time going,the flow can be regarded as steady state when the convergence criteria of |V n+1 −V n|≤10 −8 and |pn+1−pn|≤10−8 are satisfied.
The computational domain is decomposed into two rectangular sub-domains with an interface line γ12 at x=0.5.In order to assess the grid independent of this problem,four different spatial resolutions are used for the flow at Re= 1 000.The results of the velocity u profile along the vertical centerline and velocity v profile along the horizontal centerline are given in Fig.5.One can see that the present results are in good agreement with those of Ghia et al. [38] , Wahba[39] and Erturk et al. [40] ,and when the grid number is up to 32×32,the results will change no longer.Considering the computational efficiency,32×32 grid is used in the following. The velocity u profile along the vertical centerline and the velocity v profile along the horizontal centerline of the cavity are provided for different Reynolds numbers ranging from 100 to 7 500 in Fig.6.It can be seen that the present velocity profiles are in good agreement with the documented results.In addition,the evolution of the flow streamlines as the Reynolds number increases is shown in Fig.7.The main vortex is offset towards the top right corner and it moves toward the center of the cavity with the increasing of Reynolds number.Furthermore,just as demonstrated by Moffat [41] ,an infinite sequence of eddies of increasing size and strength should be observed at the corner of the cavity.As the Reynolds number increases,the driven force of the top wall against the fluid enhances.The additional small eddies first appear on the bottom corners and start to grow in size,gradually another small eddy starts to appear on the left top corner.This situation agrees with that of Ghia et al. [38] .However,some small eddies on the corner are not smooth enough.This is because of the inaccuracy producedby the singularities on the top corners of the cavity,and the global argument property of CSM,in another words, the computation at any given point depends not only on information at neighboring points,but on information from the entire domain.
 |
| Fig.5 Velocity u profile along vertical centerline and velocity v profile along horizontal centerline of cavity |
 |
| Fig.6 Velocity u profile and velocity u profile at different Reynolds numbers |
 |
| Fig.7 Streamline for cavity flow at different Reynolds numbers |
4.3 Regularized driven cavity flow in inverted L-shape geometry
The last test case is the regularized driven cavity in the inverted L-shape geometry.The top lid moves with a horizontal velocity component u(x,1)=−(1−x 2)2,and other walls keep stationary.Hugues and Randriamampianina [33] and Ehrenstein and Peyret [42] have studied the same problem,but with a square cavity.
The streamlines are shown in Fig.8 as the Reynolds number increases from 50 to 2 500.A small eddy appears on the bottom right corner of Domain I when Re= 50.As the Reynolds number increases,the influence of the driventop wall against the fluid enhances and the flow intensity in DomainⅠand Domain III is strengthened.The small eddy on the corner starts to appear and grow in size,and another two secondary eddies appear in the bottom right corners of DomainⅠand Domain III.Compared with the square cavity,the inverted L-shape geometry has more corners,so in the end,five eddies are formed.
 |
| Fig.8 Streamline for cavity flow at different Reynolds numbers |
5 Conclusions
In this paper,an efficient direct spectral domain decomposition method is developed for the solution of 2D,unsteady,and incompressible Navier-Stokes equations in irregular geometries.The computational domains are decomposed into several non-overlapping rectangular sub-domains.In each sub-domain,an improved projection scheme with second-order accuracy is used to deal with the coupling of the velocity and the pressure,and the CSM is adopted for the space discretization.The present method is direct and efficient by using the influence matrix technique to ensure the continuities of variables and their normal derivatives between adjacent sub-domains.
One problem in the solving process is that,the imposing of the Neumann boundary conditions to the Poisson equations of pressure and intermediate variable will result in the indeterminate solution.We successfully overcome this obstacle by assuming the Dirichlet boundary conditions on interface,and using the first-order normal derivatives as transmission conditions to keep the continuities of variables.Doing this,one null eigenvalue of relevant influence matrices of each variable is replaced by a nonzero value,and this action will ensure the correct solutions of gradients of pressure and intermediate variable.
The direct spectral domain decomposition method is applied to the studies of three test cases.The numerical results show that the present method can be used to efficiently study the complex fluid dynamic phenomena with spectral accuracy and without any iteration.An extension of present method to the fully 3D Navier-Stokes equations in the primitive variable formulation is in progress.
| [1] | Canuto, C., Hussaini, M. Y., Quarteroni, A., and Zang, T. A. Spectral Methods in Fluid Dynamics, Springer, New York (1988) |
| [2] | Peyret, R. Spectral Methods for Incompressible Viscous Flow, Springer, New York (2002) |
| [3] | Orszag, S. A. Spectral methods for problems in complex geometries. Journal of Computational Physics, 37(1), 70-92(1980) |
| [4] | Canuto, C. and Funaro, D. The Schwarz algorithm for spectral methods. SIAM Journal on Numerical Analysis, 25(1), 24-40(1988) |
| [5] | Pateraa, A. T. A spectral element method for fluid dynamics:laminar flow in a channel expansion. Journal of Computational Physics, 54(3), 468-488(1984) |
| [6] | Phillips, T. N. and Karageorghis, A. Efficient direct method for solving the spectral collocation equations for stokes flow in rectangularly decomposable domains. SIAM Journal on Scientific and Statistical Computing, 10(1), 89-103(1989) |
| [7] | Macaraeg, M. G. and Streett, C. L. Improvement in spectral collocation discretization through a multiple domain technique. Applied Numerical Mathematics, 2(2), 95-108(1986) |
| [8] | Zanolli, P. Domain decomposition algorithms for spectral methods. Calcolo, 24, 201-240(1987) |
| [9] | Funaro, D., Quarteroni, A., and Zanolli, P. An iterative procedure with interface relaxation for domain decomposition methods. SIAM Journal on Numerical Analysis, 25(6), 1213-1236(1988) |
| [10] | Louchart, O., Randriamampianina, A., and Leonardi, E. Spectral domain decomposition technique for the incompressible Navier-Stokes equations. Numerical Heat Transfer, Part A, 34(5), 495-518(1998) |
| [11] | Louchart, O. and Randriamampianina, A. A spectral iterative domain decomposition technique for the incompressible Navier-Stokes equations. Applied Numerical Mathematics, 33(1), 233-240(2000) |
| [12] | Pulicani, J. P. A spectral multi-domain method for the solution of 1-D-Helmholtz and Stokes-type equations. Computers & Fluids, 16(2), 207-215(1988) |
| [13] | Lacroix, J. M., Peyret, R., and Pulicani, J. P. A pseudospectral multi-domain method for the Navier-Stokes equations with application to double-diffusive convection. GAMM Conference on Numerical Methods in Fluid Mechanics, 167-174(1988) |
| [14] | Raspo, I. and Bontoux, P. Direct multidomain spectral method for the computation of various fluid dynamic problems. Journal of Applied Mathematics and Mechanics, 79(1), 33-36(1999) |
| [15] | Raspo, I., Ouazzani, J., and Peyret, R. A spectral multidomain technique for the computation of the Czochralskimelt configuration. International Journal of Numerical Methods for Heat & Fluid Flow, 6(1), 31-58(1996) |
| [16] | Bwemba, R. and Pasquetti, R. On the influence matrix used in the spectral solution of the 2D Stokes problem (vorticity-stream function formulation). Applied Numerical Mathematics, 16(3), 299-315(1995) |
| [17] | Boguslawski, A. and Kubacki, S. An influence matrix technique for multi-domain solution of the Navier-Stokes equations in a vorticity-streamfunction formulation. Journal of Theoretical and Applied Mechanics, 47(1), 17-40(2009) |
| [18] | Raspo, I. A direct spectral domain decomposition method for the computation of rotating flows in a T-shape geometry. Computers & Fluids, 32, 431-456(2003) |
| [19] | Danabasoglu, G., Biringen, S., and Streett, C. L. Application of the spectral multidomain method to the Navier-Stokes equations. Journal of Computational Physics, 113(2), 155-164(1994) |
| [20] | Sabbah, C. and Pasquetti, R. A divergence-free multidomain spectral solver of the Navier-Stokes equations in geometries of high aspect ratio. Journal of Computational Physic, 139(2), 359-379(1998) |
| [21] | Droll, P. and Schäfer, M. A pseudospectral multi-domain method for the incompressible Navier-Stokes equations. Journal of Scientific Computing, 17, 365-374(2002) |
| [22] | Chen, S. S. and Li, B. W. Application of collocation spectral domain decomposition method to solve radiative heat transfer in 2D partitioned domains. Journal of Quantitative Spectroscopy & Radiative Transfer, 149, 275-284(2014) |
| [23] | Vay, J. L., Haber, I., and Godfrey, B. B. A domain decomposition method for pseudo-spectral electromagnetic simulations of plasmas. Journal of Computational Physic, 243, 260-268(2013) |
| [24] | Grinberg, L. and Karniadakis, G. E. A new domain decomposition method with overlapping patches for ultrascale simulations:application to biological flows. Journal of Computational Physic, 229(15), 5541-5563(2010) |
| [25] | Sidler, R., Carcione, J. M., and Holliger, K. A pseudo-spectral method for the simulation of poroelastic seismic wave propagation in 2D polar coordinates using domain decomposition. Journal of Computational Physic, 235, 846-864(2013) |
| [26] | Golbabai, A. and Javidi, M. A spectral domain decomposition approach for the generalized Burger's-Fisher equation. Chaos, Solitons and Fractals, 39(1), 385-392(2009) |
| [27] | Taleei, A. and Dehghan, M. Time-splitting pseudo-spectral domain decomposition method for the soliton solutions of the one- and multi-dimensional nonlinear Schrödinger equations. Computer Physics Communications, 185(6), 1515-1528(2014) |
| [28] | Hameed, M. and Ellahi, R. Numerical and analytical solutions of an Oldroyd 8-constant MHD fluid with nonlinear slip conditions. International Journal for Numerical Methods in Fluids, 67(10), 1234-1246(2011) |
| [29] | Hameed, M. and Ellahi, R. Thin film flow of non-Newtonian MHD fluid on a vertically moving belt. International Journal for Numerical Methods in Fluids, 66(11), 1409-1419(2011) |
| [30] | Ellahi, R. Numerical analysis of steady non-Newtonian flows with heat transfer analysis, MHD and nonlinear slip effects. International Journal of Numerical Methods for Heat & Fluid Flow, 22(1), 24-28(2012) |
| [31] | Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe:analytical solutions. Applied Mathematical Modelling, 37(3), 1451-1467(2013) |
| [32] | Luo, X. H., Li, B. W., Zhang, J. K., and Hu, Z. M. Simulation of thermal radiation effects on MHD free convection in a square cavity using Chebyshev collocation spectral method. Numerical Heat Transfer, Part A, 66(7), 792-815(2014) |
| [33] | Hugues, S. and Randriamampianina, A. An improved projection scheme applied to pseudospectral methods for the incompressible Navier-Stokes equations. International Journal for Numerical Methods in Fluids, 28(3), 501-521(1998) |
| [34] | Tuckerman, L. S. Divergence-free velocity fields in nonperiodic geometries. Journal of Computational Physics, 80(2), 403-441(1989) |
| [35] | Chen, H. L., Su, Y. H., and Shizgal, B. D. A direct spectral collocation Poisson solver in polar and cylindrical coordinates. Journal of Computational Physics, 160(2), 453-469(2000) |
| [36] | Johnston, H. and Liu, J. G. Accurate, stable and efficient Navier-Stokes solvers based on explicit treatment of the pressure term. Journal of Computational Physics, 199(1), 221-259(2004) |
| [37] | Burggraf, O. R. Analytical and numerical studies of the structure of steady separated flows. Journal of Fluid Mechanics, 24(1), 113-151(1966) |
| [38] | Ghia, U., Ghia, K. N., and Shin, C. T. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. Journal of Computational Physics, 48(3), 387-411(1982) |
| [39] | Wahba, E. M. Steady flow simulations inside a driven cavity up to Reynolds number 35000. Computers & Fluids, 66, 85-97(2012) |
| [40] | Erturk, E., Corke, T. C., and Gokcol, C. Numerical solutions of 2D steady incompressible driven cavity flow at high Reynolds numbers. International Journal for Numerical Methods in Fluids, 48(7), 747-774(2005) |
| [41] | Moffat, H. K. Viscous and resistive eddies near a sharp corner. Journal of Fluid Mechanics, 18(1), 1-18(1964) |
| [42] | Ehrenstein, U. and Peyret, R. A Chebyshev collocation method for the Navier-Stokes equations with application to double-diffusive convection. International Journal for Numerical Methods in Fluids, 9(4), 427-452(1989) |
 2015,Vol.36
2015,Vol.36




































