Shanghai University
Article Information
- Wentang WU, Yanji HONG, Baochun FAN. 2015.
- Numerical investigation of turbulent channel flow controlled by spatially oscillating spanwise Lorentz force
- Appl. Math. Mech. -Engl. Ed., 36(9): 1113-1120
- http://dx.doi.org/10.1007/s10483-015-1972-6
Article History
- Received Jun. 3, 2014;
- in final form Jan. 27, 2015
2. National Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China;
3. National Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China
The nature and significance of organized large-scale structures,e.g.,streaky structures and vortical structures,in turbulent boundary layers have been extensively studied for over six decades[1, 2, 3, 4, 5]. It has been recognized that most high skin-friction drags are attributed to the existence of the near-wall vortical structures,e.g.,quasi-streamwise vortices (QSVs),hairpin vortices,and soliton-like coherent structures (SCSs)[6, 7],and the associated ejection/sweep events.
Kim and Bewley[8] and Kim[9] proposed that the near-wall streamwise vortices were the most important turbulent structure in drag manipulation. Various methods have been proposed, focusing on the suppression of the near-wall coherent structures,e.g.,wall oscillation[10, 11, 12], deformed wall[13, 14, 15],blowing and suction wall[16, 17],and turbulent flows around cylinders[18, 19].
In this paper,the spatially oscillating spanwise Lorentz force is used to control the near- wall turbulence. A statistically steady flow field with well-organized streamwise vortices is maintained via the Lorentz force. The drag decreases considerably due to the suppression of the near-wall coherent structures. A formulation expressing the relation between the Reynolds shear stress and the skin-friction drag is derived for the further discussion of the drag reduction.
2 Numerical calculations 2.1 Governing equation
The discussed problem is the control of the Lorentz force for a fully developed turbulent flow in a weakly conductive fluid in a channel mounted with electromagnetic actuators on both the upper and lower walls. The flow is governed by the incompressible Navier-Stokes (N-S) equations with the externally imposed Lorentz force term written as follows:
where all variables are nondimensionalized with respect to the channel half width h and the center line velocity Uc. u is the velocity vector. p is the pressure. Re is the Reynolds number. f is the Lorentz force per unit mass,and it is given by where in which A is the non-dimensional amplitude of excitation (or interaction parameter),δ is the effective penetration of the Lorentz force,and Lx is the streamwise length of the computational domain.kxis the streamwise wave number,and it is defined by where λx is the wavelength along the streamwise direction.The numerical method adopted here is based on the standard Fourier-Chebyshev spectral method. The usual no-slip and no-penetration conditions are applied at the wall,and the periodic conditions are imposed along the homogeneous directions[20, 21]. The time advance- ment is carried out by a semi-implicit back-differentiation formula method with the third-order accuracy.
Figure 1 shows a schematic diagram of the computational domain. The computational domain size is (4φ/3)× 2 × (2φ/3) (approximately 754×360×377 wall units),corresponding to the streamwise,normal,and spanwise directions,respectively. The grid spacing is uniform in the homogeneous directions. More details are referred to Refs. [18] and [19].
 |
| Fig. 1 Schematic diagram of computational domain |
The flow control by the Lorentz force begins at t = 200 when the initial disturbance in- duced for generating the fully developed turbulence has been essentially eliminated. Then,the turbulence statistics is performed from t = 500 to t = 1 000.
2.2 Skin frictional drag in turbulent channel flow
The skin frictional drag of a wall-bounded turbulent flow is attributed to the existence of the near-wall vortical structure and the associated ejection/sweep events. For the channel flow with a constant flux,a relation between the skin friction coefficient and the Reynolds stress distribution is derived as follows.
If the Reynolds decomposition is applied in Eq.(1) in the x-direction,based on the base- fluctuation decomposition with the base flow U(y) = 1 − (1 − y)2,we have
whereBased on the assumption of the periodic flow structures in the homogeneous directions and the no-slip boundary conditions,which are the basic features of the turbulent wall-bounded flow,we average Eq.(5) by the integration in both the x-direction and the z-direction,i.e.,the homogeneous directions,and obtain
where the overbar “-” denotes an average over a plane with a constant y.Integrating Eq.(6) over y gives
where Cf is the skin friction coefficient defined by in which Uc is the center line velocity.Substituting Eq.(7) into Eq.(6) yields
Substituting the triple integration,i.e.,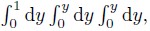 into Eq.(8),we have
For the stationary turbulence,
Therefore,
where all variables are normalized by the channel half width and the center line velocity. u′v′
is the Reynolds shear stress produced directly by the ejection (v′ > 0) and sweep (v′ < 0)
activities. This equation shows that the skin-friction drag in a turbulent channel flow consists
of the laminar drag and the y-weighted integration of u′v′,which is regarded as a streamwise
momentum transform in the wall-normal direction. The sweep activities are more significant
than the ejection activities in the vicinity of the wall due to the effects of the bursting events,
which can create the regions of the high skin-friction and cause the y-weighted integration of
u′v′ to be always positive.
into Eq.(8),we have
For the stationary turbulence,
Therefore,
where all variables are normalized by the channel half width and the center line velocity. u′v′
is the Reynolds shear stress produced directly by the ejection (v′ > 0) and sweep (v′ < 0)
activities. This equation shows that the skin-friction drag in a turbulent channel flow consists
of the laminar drag and the y-weighted integration of u′v′,which is regarded as a streamwise
momentum transform in the wall-normal direction. The sweep activities are more significant
than the ejection activities in the vicinity of the wall due to the effects of the bursting events,
which can create the regions of the high skin-friction and cause the y-weighted integration of
u′v′ to be always positive.
2.3 Flow induced by spatially oscillating spanwise Lorentz force
The spatially oscillating Lorentz force fz defined by Eqs. (3) and (4) is independent of time. The amplitude of the Lorentz force oscillates sinusoidally in the x-direction,and decays exponen- tially along the y-direction (see Fig. 2(a)). When this force is introduced into a static flow field, a generalized Stokes-layer is then created. The distributions of the induced spanwise velocity are shown in Fig. 2(b),where the red areas (deep-colored areas at the front tips) refer to the positive velocity,and the blue areas (deep-colored areas at the back tips) refer to the negative velocity. The distributions of the induced spanwise velocity,when a laminar flow is introduced,are shown in Fig. 2(c). Due to the main flow,the red and blue areas (the deep-colored areas) are overlaid at nλx/2 (n ∈ N) to form the inclined shear layers (see Fig. 2(d)). From Fig. 2,we can see that there is no vortex in the induced Stokes-layer.
 |
| Fig. 2 Lorentz force distribution and induced flow field |
Within the viscous sublayer (y+ < 5),assume that the mean velocity profile is linear. Then, the wall shear stress is
Therefore,the skin-friction drag can be obtained from the measured mean streamwise velocity for a position in the viscous sublayer.The percentage of the drag reduction rate is simply given by
where (τw)i denotes the average wall shear stress with the Lorentz force control,and (τwn)ni denotes the average wall shear stress without control.The calculated drag reduction,as a result of the Lorentz force control,is presented in Fig. 3, where Fig. 3(a) shows the drag reduction variation with the wave numberkxwhen δ = 0.02 and A = 1.0,and Fig. 3(b) shows the drag reduction variation with the amplitude A when δ = 0.02 andkx= 3. The results indicate that the largest drag reduction is about 62%,occurring at kx = 3 (see Fig. 3(a)) and about 62% at A = 1.0 (see Fig. 3(b)). Therefore,the skin-friction drag can be reduced significantly by an appropriate combination of the amplitude and the wave number.
 |
| Fig. 3 Drag reduction under spanwise Lorentz force control |
Due to the spatially oscillating spanwise Lorentz force when A = 1.0,kx= 3,and δ = 0.02, the near-wall turbulent flow is modified by an additional induced flow. The evolutions of the streaks and the vortex structures in the near-wall region in the controlling process are illustrated in Fig. 4,where the blue areas (deep-colored areas in the right-side subfigures of Figs. 4(a),4(b), and 4(c),the middle part of the left-side subfigure of Fig. 4(a),and the left-side subfigure of Fig. 4(c)) represent the low-speed streaks,and the red areas (deep-colored areas in the upper and lower parts of the left-side subfigure of Figs. 4(a) and the left-side subfigure of Fig. 4(b)) represent the high-speed streaks. The left column shows the streaky structures. The right column shows the vortex structures when 0 < y+ < 100. At t = 200,before actuating,the meandering and irregular streaky structures and the characteristic structures of the longitudinal vortices (e.g.,quasi-streamwise vortices and horseshoes vortices) are exhibited. Subsequently, these intrinsic coherent structures become more and more well-organized. Finally,the flow is maintained at a statistically steady state via the oscillating Lorentz force (see Fig. 4 at t = 340), where the vortex shape is very similar to each other,and all vortices are well organized.
 |
| Fig. 4 Evolutions of streaks and vortex structures near wall |
The typical streamwise vortex structures are shown in Fig. 5,where the red area (the lower deep-colored area) and the blue area (the upper deep-colored area) represent,respectively,the positive and negative values of the vorticity,which are denoted by SP and SN,respectively. It is shown that the positive vortex is tilted with the negative tilting angle of about −32®,while the negative vortex is titled with the positive tilting angle of about 32®. Each vortex has an averaged streamwise length of 0.5λx (about 200 wall units). The intervals of 0.5λx and 0.3λx in the streamwise and spanwise directions,respectively,overlay with each other with opposite signs at nλx/2 (n ∈ N).
 |
| Fig.5 Isosurface of SP and SN in controlled turbulent channel flow |
The profiles of the Reynolds shear stress are shown in Fig. 6. It is shown that the Reynolds shear stress u′v′ is weakened considerably by the control,especially in the near-wall area.
 |
| Fig. 6 Distribution of u′v′ in controlled and uncontrolled turbulent channel flows |
A formulation of the skin-friction drag in the turbulent channel flow related to the Reynolds shear stress is derived. It shows that the turbulent drag consists of the laminar drag and the y-weighted integration of u′v′,which are directly related to the turbulent coherent structures.
The spatially oscillating spanwise Lorentz force with several proper control parameters can control the near-wall turbulence well. The controlled flow is finally stabilized at a statisti- cally steady state via the Lorentz force so that the streamwise vortices can be well organized, whereas few hairpin vortices are found. Consequently,the Reynolds shear stress is weakened considerably in all controlled flow fields,resulting in the drag reduction.
| [1] | Theodorsen, T. Mechanism of turbulence. Proceedings of the 2nd Midwestern Conference on Fluid Mechanics, Ohio State University, Ohio, 1-18(1952) |
| [2] | Kline, S. J., Reynolds, W. C., Schraub, F. A., and Runstadler, P. W. The structure of turbulent boundary layers. Journal of Fluid Mechanics, 30, 741-773(1967) |
| [3] | Cantwell, B. J. Organized motion in turbulent flow. Annual Review of Fluid Mechanics, 13, 457-515(1981) |
| [4] | Kim, J., Moin, P., and Moser, R. D. Turbulence statistics in fully developed channel flow at low Reynolds number. Journal of Fluid Mechanics, 177, 133-166(1987) |
| [5] | Blackwelder, R. F. and Kaplan, R. E. On the wall structure of the turbulent boundary layer. Journal of Fluid Mechanics, 76, 89-112(1976) |
| [6] | Lee, C. B. and Wu, J. Z. Transition in wall-bounded flows. Applied Mechanics Reviews, 61, 030802(2008) |
| [7] | Lee, C. B. and Lee, R. Q. Dominant structure for turbulent production in a transitional boundary layer. Journal of Turbulence, 8, 1-34(2007) |
| [8] | Kim, J. and Bewley, T. R. A linear systems approach to flow control. Annual Review of Fluid Mechanics, 39, 383-417(2007) |
| [9] | Kim, J. Physics and control of wall turbulence for drag reduction. Philosophical Transactions of the Royal Society, A:Mathematical, Physical and Engineering Sciences, 369, 1396-1411(2011) |
| [10] | Choi, K. Near-wall structure of turbulent boundary layer with spanwise-wall oscillation. Physics of Fluids, 14, 2530-2542(2002) |
| [11] | Ricco, P. and Wu, S. On the effects of later wall oscillation on a turbulent boundary layer. Experimental Thermal and Fluid Science, 29, 41-52(2004) |
| [12] | Quadrio, M., Ricco, P., and Viotti, C. Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction. Journal of Fluid Mechanics, 627, 161-178(2009) |
| [13] | Kang, S. and Choi, H. Active wall motions for skin-friction drag reduction. Physics of Fluids, 12, 3301-3304(2000) |
| [14] | Endo, T., Kasagi, N., and Suzukin, Y. Feedback control of wall turbulence with wall deformation. International Journal of Heat and Fluid Flow, 21, 568-575(2000) |
| [15] | Shen, L., Zhang, X., Yue, K. P., and Triantafyllou, M. S. Turbulent flow over a flexible wall undergoing a streamwise traveling wave motion. Journal of Fluid Mechanics, 484, 197-221(2003) |
| [16] | Min, T., Kang, S. M., Speyer, J. L., and Kim, J. Sustained sub-laminar drag in a fully developed channel flow. Journal of Fluid Mechanics, 558, 309-318(2006) |
| [17] | Lee, C., Min, T., and Kim, J. Stability of channel flow subject to wall blowing and suction in the form of a traveling wave. Physics of Fluids, 20, 10153(2008) |
| [18] | Zhang, H., Fan, B. C., Chen, Z. H., and Li, Y. L. Underlay mechanism in lift-drag phase diagrams for shear flow over cylinder. Applied Mathematics and Mechanics (English Edition), 35(2), 221-228(2014) DOI 10.1007/s10483-014-1785-8 |
| [19] | Zhu, Z. J., Niu, J. L., and Li, Y. L. Swirling-strength based large eddy simulation of turbulent flow around single square cylinder at low Reynolds numbers. Applied Mathematics and Mechanics (English Edition), 35(8), 959-978(2014) DOI 10.1007/s10483-014-1847-7 |
| [20] | Huang, L. P., Fan, B. C., and Dong, G. Turbulent drag reduction via a transverse wave travelling along streamwise direction induced by Lorentz force. Physics of Fluids, 22, 015103(2010) |
| [21] | Wu, W. T., Hong, Y. J., and Fan, B. C. Vortex structures in turbulent channel flow modulated by spanwise Lorentz force with steady distributions. Acta Physica Sinica, 63, 054702(2014) |
 2015, Vol. 36
2015, Vol. 36
















