Shanghai University
Article Information
- Haijue XU, Yuchuan BAI. 2015.
- Theoretical analyses on hydrodynamic instability in narrow deep river with variable curvature
- Appl. Math. Mech. -Engl. Ed., 36(9): 1147-1168
- http://dx.doi.org/10.1007/s10483-015-1971-6
Article History
- Received May 30, 2014;
- in final form Jan. 28, 2015
2. Institute for Sedimentation on River and Coastal Engineering, Tianjin University, Tianjin 300072, China
Because of the various geological and climatic conditions of different basins,river morphology is complex and diverse. According to the morphological characteristics,natural rivers can be approximately classified into four types,i.e.,straight,bending,braided,and wandering. Bending river is also known as meandering river,and it is the most common and healthy morphology in nature[1]. With the inner properties,bending river will continuously swing, migrate,and detour as time goes on,which forms a complex dynamic process[2]. The dynamic process of bending river is not only the core content of most theoretical river studies but also the focus of practical river engineering[3, 4]. In the middle and lower reaches of the Yellow River and the Yangtze River,the bending shapes not only can change the flow structures,but also can lead to the lateral scouring and creeping of the river[5].
River morphology is the consequence of the interaction between the flow and the sediment. Meanwhile,the change of river morphology can affect the flow structure. When the irregular boundaries of riparian or riverbed are contacted,the flow will generate a certain frequency of disturbance,which may be in the growing,decaying,or neutral state. When the disturbance is in its growing state,the laminar flow will become turbulent,and large scales of vortexes may appear,inducing the migration of the river. When it is in its neutral state,the original disturbance will keep its form,and evolve for a long time,shaping the configuration of the river continuously[6, 7]. Therefore,river is a dynamic system containing the interaction between the flow and the sediment. On one hand,the swing of the river bank and the evolution of the river morphology are macro performances of the mesoscopic movement of the sediment and flow[8]. On the other hand,the river morphology has great effects on the dynamic characteristics of the flow motion[9].
Compared with those of straight channels,the instability modes of bending rivers vary with the wavy characteristics of the bending rivers[10]. In straight channels,the flow instability occasionally happens,and the streamline may change from straight to bending[11]. In bending rivers,the change trend of the flow instability is more obvious,which can be induced not only by the flow properties but also by the wavy characters of the boundary. In mathematics,the traditional Lyapunov problem changes into a Floquet-Lyapunov problem. The generation of the hydrodynamic structure of the bending river changes the sediment transportation and river bank erosion,further enhancing the bending of the river[12, 13].
Therefore,based on the concept of the flow stability,the topic of the flow stability in bending rivers can be considered as a new issue of river dynamics as well as a traditional issue of fluid mechanics. It contains two aspects,i.e.,the disturbance and the effects of the bending channel on the flow instability. The disturbance,which is caused by the curvature-induced flow instability, will promote the evolution from straight to bending[14]. The effects of the bending channel on the flow instability exist in the process of the large-scale vortex structure evolution and the process of the suspension and sediment transportation in the turbulent flow[15, 16]. Monson et al.[17] and Jiang and Lakashminarayana[18] pointed out that the stability characteristics of the bending river were different from those of the straight river. Therefore,in river dynamics,the studies on the second side are of great significance,and it must be considered.
In this paper,a theoretical model of the dynamic stability of a bending channel is established. The transform characteristics from the laminar flow to the turbulent flow in a narrow deep channel with a variable curvature are studied. The variations of some parameters concerning the flow stability characteristics of the bending river,such as the curvature,the wave number, and the wave frequency,are obtained. This paper is divided into four sections. The first section is introduction. The second section is the theoretical model. The third section is the certification and discussion of the obtained results. And the last section is the conclusions.
2 Theoretical modelRivers in nature can be classified into four types,i.e.,straight,meandering,braided,and wandering,among which the meandering type is the most common and stable morphology.
The coordinate system is shown in Fig. 1,where the bending river with a small curvature is considered. The x-axis and the normal direction of the z-axis are parallel to the bottom,and the y-axis is perpendicular to the xOz-plane,where J is the bottom slop defined by J = sinθ.
 |
| Fig. 1 Schematic diagram of coordinate axis |
The morphology of the bending river with a small curvature is shown in Fig. 2.
 |
| Fig. 2 Morphology of bending river |
Since the configuration and the characteristics of a river are like those of a wave,the parameters of the river are defined like those of the wave. In mathematics,it is expressed as follows:
where in which A is the amplitude of the bending,b is one half of the river width,and εΨ represents the relative deviation amplitude of the bending river from the straight channel. αf is the wave number of the river. ωg is the wave frequency,which represents the propagating frequency of the river. C represents the propagating speed of the river,and it is defined by Since the spatial model is used in the text,αf is real and positive,and ωg may be positive, negative,or even complex. Therefore,whether the wave can propagate upward or downward is determined by the positive or negative sign of the real part of ωg. 2.1 Governing equationIn the xOz-plane,taking into account the morphology of the river with a small curvature (see Fig. 2(a)),we introduce the coordinate transform as follows[10]:
Transform the physical coordinate into the computational coordinate (see Fig. 2(b)),where s is the flow direction,n is the normal direction of the x-axis,and η is the upward direction perpendicular to the xOz-plane. Then,the Navier-Stokes equations under the coordinate system of (s,η,n) can be obtained as follows: The continuity equation is The momentum equations are where ∇2 is the dimensional Laplace operator defined by 2.2 Dimensionless
There are two spatial scales in the equations. One is the horizontal scale described by the
half river width b,and the other is the vertical scale described by the river depth H. Therefore,
a new parameter describing the ratio of the depth to the half of the river width,i.e., appears. Combining the maximum velocity of the laminar flow U with the time
appears. Combining the maximum velocity of the laminar flow U with the time  ,we have
,we have
As mentioned above,εΨ represents the relative deviation amplitude of the bending river from the straight channel. For a bending river with a very small deviation,εΨ is often smaller than 1. Therefore,the solution of the laminar flow of the bending river can be divided into two parts,i.e.,
where u,v,w,and p represent the solution of the laminar flow of the bending river. U,V , W,and P represent the solution of the laminar flow of the straight channel. uΨ,vΨ,wΨ,and pΨ represent the modification to the variables when bending occurs. The magnitude of these modifications is of the same order with εΨ . If only small deviations are considered,then εΨ < 1. 2.3.1 Basic flow equation and its solutionFrom the content mentioned above,we know that εΨ is the relative deviation amplitude of the bending river to the straight channels,and it is defined by
εΨ = 0 means A = 0,namely,there is no deviation between the straight river and the bending river. Then,the solution of the equations of the bending river can be taken as that of the straight channel.(i) Basic flow equations
Substituting εΨ = 0 into Eqs. (5)-(8) and rewriting u,v,w,and p of the original equations into U,V ,W, and P yield the equations of the straight river. The solution of U,V ,W, and P is the solution of the equation of the straight river.
where ∇2 is the dimensionless Laplace operator in the equations of the straight river defined by (ii) Solution of equation of basic flow
Consider the steady uniform laminar flow in the considered straight channel,i.e.,W = 0,
V = 0, and
and  We can simplify the equations as follows:
We can simplify the equations as follows:
(i) Modification equations ( εΨ )
Let Eqs. (5)-(8) subtract the corresponding equations of Eqs. (10)-(13). Then,the equations that satisfy the bending-induced modification can be obtained as follows:
The orders of Eqs. (20)-(23) are εΨ which means that the modifications due to the bending are of the same order with the relative deviation amplitude of the bending river from the straight channel.(ii) Solution of modification quantities
If the river is narrow and deep,then
The terms containing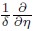 can be taken as the value far smaller than 1. Then,the original
equations can be simplified to a quasi-three-dimensional (3D) form. Moreover,let
Then,the solution can be written as follows:
where
Equations (20)-(23) can be rewritten as follows:
where D = d/dy is a differential operator.
can be taken as the value far smaller than 1. Then,the original
equations can be simplified to a quasi-three-dimensional (3D) form. Moreover,let
Then,the solution can be written as follows:
where
Equations (20)-(23) can be rewritten as follows:
where D = d/dy is a differential operator.
Correspondingly,the boundary conditions can be rewritten as follows:
Equations (25) and (26) can be solved separately. The latter gives vˆΨf = 0. Therefore,if no resonance,force motion,or variation of the velocity along the z-direction is considered,there is no secondary flow in that direction.Figures 3 and 4 show the variations of the modified velocities wΨ and uΨ along the river width,respectively. It can be seen that the magnitudes of the modified velocities uΨ and wΨ are not always equal to zero. In addition,the value of uΨ is almost two orders of magnitude higher than that of wΨ. Moreover,due to the effects of the bending,uΨ gets its maximal value near the convex and concave banks.
 |
| Fig. 3 Variations of modified velocity w along river width |
 |
| Fig. 4 Variations of modified velocity u along river width |
The solution of uΨ,ˆvΨf,wΨ,and pΨ can be considered as the modification to the basic quantities. Therefore,the solution of the laminar flow of the bending river is actually the sum of the velocity distribution of the straight channel and the bending modification. Figure 5 shows the velocity distribution and the dynamic axis of the laminar flow in the bending river. It can be seen that because of the bending,the velocity distribution of each section changes. In addition,the dynamic axis of the bending river deviates a little bit from that of the straight channel,which swings within the amplitude range of the river. For a bending river,such a velocity distribution seems to be more fit to the flow characteristics of the “great flow”,i.e., the great flow trends to be straight,whereas the small flow stays meandering[19]. While other characteristics of the “great flow” are the large discharge and the high water level,which are in accord with the characteristics of the narrow deep river.
 |
| Fig. 5 Velocity distribution and dynamic axis of flow in bending river |
We add some disturbed quantities into the basic solution of the laminar flow,i.e.,let
Compared with Eq. (9),some terms such as uT ,vT ,wT ,and pT are added in Eq. (31),which can be considered as the small disturbances acting on the flow of the channel. εTrepresents the scale of the small disturbances,which is not so closely associated with the bending scale εΨ and can be considered to be a small quantity.
(i) Equations of disturbed quantities (εT)
Substituting Eq. (31) into Eqs. (5)-(8) and subtracting the corresponding parts of Eqs. (10)- (13) and Eqs. (20)-(23) in succession,we can obtain the equations which can judge the stability of the laminar flow. The details are as follows:
(ii) Solution of disturbed quantitiesIn Eqs. (32)-(35),the known functions are the solutions of the laminar flow in the straight channel,and the unknown functions are uT ,vT ,wT ,and pT ,whose coefficients are all periodic with ζ and τ. Therefore,according to the Floquet theory[20, 21],the solution can be written as follows:
where αT is the wave number of the disturbance. ωT is the frequency of the disturbance,which is known as the Floquet exponent. If it is a temporal-mode question,then the wave number αT is a real number,whereas the frequency ωT is a complex number.Substituting Eq. (36) into Eqs. (32)-(35) gives the generalized Orr-Sommerfeld (O-S) equations expressed as follows:
The above equations are the O-S equations,which describe the hydrodynamic instability characteristics of the laminar flow in the bending channels. Different from the traditional O-S equations,some bending effects are added,which can be reflected through several parameters. The value of εΨ not only can reflect the relative deviation amplitude of the bending river to the straight channel,but also can determine the amplitude of the modification. The effects of this parameter are also brought into the final O-S equation,influencing the hydrodynamic instability characteristics of the bending river. The wave number αf and the wave frequency ωg can affect the global hydrodynamic instability,and reflect the characteristics of the river morphology and evolution,respectively. Therefore,in view of the relationship of the classical O-S equation f(Re,αT ,ωT ) = 0,we can express the O-S equation describing the hydrodynamic instability characteristics of the laminar flow in the bending channel as follows:
where Re,αT ,and ωT are the main variables,and εΨ αf ,and ωg are the parametric variables.The equations change a little due to the bending. It contains not only the unknown ûTn(η), but also other characteristic functions such as ûTn-1(η),ûTn+1(η),ŵTn(η),and &pcirc;Tn(η),which cannot be solved separately. According to the general method[21],truncation is applied at
In other words,when |n| > 1,all the functions of are set to be zero. Then,the 12 unknown functions are Let Then,there are 12 equations for these unknowns. Therefore,this problem is solvable. If ûΨi = 0 is considered,then Eq. (54) can be solved separately. The problem with 12 equations can be decomposed into a problem with 9 equations and a problem with 3 equations.Using the spectrum method to discretize the equations,we can obtain the hydrodynamic instability characteristics of the laminar flow in the bending river with the quick response (Q-R) method combined with the Muller method[22, 23, 24].
3 Results and analyses 3.1 Verification of computed resultsThe neutral curve subject to the condition of εΨ = 0 is the curve of the straight channel. For the issue in this paper,when εΨ = 0,we degrade the studied problem to a stability problem of the plane Poiseuille flow.
(i) Verification of characteristic frequency If
then we can obtain the eigenvalue of the equation as follows: which is the same as that obtained by Orszag[25] in the plane Poiseuille flow under the same condition (ii) Verification of critical Reynolds number If then we can obtain the critical Reynolds number Recr and the critical disturbance wave number αT as follows: These results are almost the same as those obtained by Orszag[25] in the plane Poiseuille flow under the same condition. Moreover,the computed characteristic frequency in this paper is ωT = 0.269 429 32. The characteristic frequency obtained by Orszag[25] is This also proves the validity of the model.(iii) Verification of neutral curves
Figure 6 shows the verification of the theoretical results on the neutral curves of the straight channel. As shown in Fig. 6,the theoretical results in this paper agree well with the numerical results of Reynolds and Potter[26] and the experimental results of Nishioka and Ichikawa[27].
 |
| Fig. 6 Verification of computed results on neutral curves of straight channel |
In the light of the analyses on the above three aspects,we have proved the validity of the model. Therefore,the results of this model can be adopted to discuss the hydrodynamic instability characteristics of the laminar flow in the narrow-deep bending channel.
3.2 Hydrodynamic instability characteristics of laminar flow in bending river 3.2.1 Variations of eigenvalues with relative deviation amplitude(i) Variations of characteristic frequency and characteristic growth rate with relative deviation amplitude
Curvature is an important parameter to characterize a river,which can be measured by the
deviation amplitude  b of the bending river from the straight channel. The occurrence of
the bending is equivalent to an added shape to the straight channel,which not only can change
the flow structure of the river,but also can affect the hydrodynamic instability characteristics
of the laminar flow. Table 1 shows the variations of the real parts and the imaginary parts of
the frequency when
b of the bending river from the straight channel. The occurrence of
the bending is equivalent to an added shape to the straight channel,which not only can change
the flow structure of the river,but also can affect the hydrodynamic instability characteristics
of the laminar flow. Table 1 shows the variations of the real parts and the imaginary parts of
the frequency when
The positive imaginary parts of the eigenvalues mean that the amplitude of the disturbance increases when time goes on,and vice versa. For example,if εΨ < 0.02,the amplitude of the disturbance will decrease when time goes on,while if εΨ > 0.02,the amplitude of the disturbance will increase as time goes on. Moreover,it can be seen from Table 1 that the imaginary part of the disturbance decreases at first,and then increases. Therefore,the growth rate of the disturbance amplitude decreases at first,and then increases.
The real part of the eigenvalue represents the frequency of the disturbance. As shown in Table 1,the characteristic frequency decreases slowly when the relative deviation amplitude increases. Therefore,it can be concluded that the period of the disturbance will slowly become longer.
Theoretical analyses on hydrodynamic instability in narrow deep river with variable curvature 1161
(ii) Variations of neutral curves with relative deviation amplitude
Neutral curve is very important in analyzing the hydrodynamic instability characteristics of the laminar flow,which can distinguish the stable region of the laminar flow from the unstable region that may transform to turbulence. It can be seen from Fig. 6 that the left sides of the neutral curves have smaller Reynolds numbers and belong to the stable region of the laminar flow,whereas the right sides have relatively larger Reynolds numbers and correspond to the unstable region of the laminar flow.
Figure 7 shows the comparison of the neutral curves under different deviation amplitudes. As shown in Fig. 7,the neutral curves move to the right at first,and then move to the left when the relative deviation amplitude εΨ increases. Moreover,the curves tend to be straight, and the critical wave number tends to decrease at first,and then increases rapidly. When εΨ = 0.05,the critical Reynolds number is 2 500,and the critical wave number is larger than 1.2.
 |
| Fig. 7 Comparison of neutral curves under different deviation amplitudes |
(iii) Variations of characteristic frequency contour with relative deviation amplitude
For a temporal mode,the characteristic wave number αT is real,and the characteristic frequency ωT is complex,whose imaginary part represents the increasing amplitude of the disturbance. When the imaginary part of the eigenvalue equals zero,the corresponding curve is called the neutral curve,whose amplitude will not change as time goes on.
The positive imaginary parts mean that the amplitude of the disturbance will increase continuously. The laminar flow will become unstable due to the disturbance. The corresponding region is known as the unstable region,whereas the negative imaginary parts mean that the amplitude of the disturbance will decrease slowly. The laminar flow will stay stable. Therefore, the corresponding region is stable.
Figures 8 and 9 show the contours of the imaginary parts of the characteristic frequency ωTi with the relative deviation amplitudes being 0.018 and 0.036,respectively. As shown in Figs. 8 and 9,the imaginary parts of the characteristic frequencies of both εΨ = 0.018 and εΨ = 0.036 show a slower decreasing tendency when the Reynolds number increases. That is to say,the distributions of the contours become scattering on the right-side of the figure. The comparison between the two figures also shows that the contour distribution of εΨ = 0.018 is even more scattered than that of εΨ = 0.036.
 |
| Fig. 8 Contours of imaginary part of charac- teristic frequency when εΨ = 0.018 |
 |
| Fig. 9 Contours of imaginary part of charac-teristic frequency when εΨ = 0.036 |
The real part of the characteristic frequency represents the frequency of the disturbance. The larger its value is,the higher the instability frequency is and the shorter the period of the disturbance is. Figures 10and 11 show the contours of the real parts of the characteristic frequency ωTr with the relative deviation amplitudes of 0.018 and 0.036,respectively. It can be seen from the figures that the real part of the characteristic frequency is closely related to the Reynolds number Re and the wave number αT . The real part of the frequency is larger when the contours are on the top left corner of the figure,and is smaller when the contours are on the bottom right corner of the figure. The results suggest that both the decrease in the Reynolds number and the increase in the wave number lead to the increase in the frequency.
 |
| Fig. 10 Contours of real part of characteristic frequency when εΨ = 0.018 |
 |
| Fig. 11 Contours of real part of characteristic frequency when εΨ = 0.036 |
Although the contours of the imaginary part of the frequency with the relative deviation amplitude of 0.018 are quite different from those of 0.036,the comparison between Figs. 10 and 11 shows that their real parts are quite similar,whose numerical difference is within 15% of the total value.
3.2.2 Variations of eigenvalues with wave number(i) Effects of wave number on frequency
As mentioned above,the wave number,i.e.,the curve number per unit length,is another important parameter that affects the hydrodynamic instability characteristics of the laminar flow. The increase in the wave number means the decrease in the wave length. Figures 12 and 13 show the variations of the imaginary part and the real part of the characteristic frequency with different deviation amplitudes and varying wave numbers.
 |
| Fig. 12 Variations of imaginary part of charac- teristic frequency with different εΨ and varying αf |
 |
| Fig. 13 Variations of real part of character- istic frequency with different εΨ and varying αf |
It can be seen from Figs. 12 and 13 that the imaginary part and the real part of the frequency of the straight river do not change when the wave number increases,which is in accord with the above discussion. While those of the bending river with the relative deviation amplitude being 0.018 and 0.036 tend to increase at first,and then decrease rapidly. The comparison between the curves of two different relative deviation amplitudes in Fig. 12 shows that more instability is brought into the laminar flow of the river when the relative deviation amplitude increases. That is to say,when the relative deviation amplitude is 0.036,most wave numbers are in the unstable region,while when the relative deviation amplitude is 0.018,only a few wave numbers are in the unstable region. It can be seen from Fig. 13 that the real part of the characteristic frequency decreases rapidly when the wave number increases,especially in the rivers with large relative deviation amplitudes.
There are many factors related to the river morphology,among which the hydrodynamic characteristics of the flow are the most important.
The variations of the characteristic frequency with different river wave numbers and varying deviation amplitudes are shown in Figs. 14 and 15,respectively. It can be seen from Fig. 14 that the river with different wave numbers corresponds to that with different stable relative deviation amplitudes (the minimum growth rate). The smaller the relative deviation amplitude is,the larger the wave number is,the longer the river wave length is,and the greater the flow inertia is,representing the characteristics of the “great flow”. Moreover,the larger the relative deviation amplitude is,the larger the wave number is,the shorter the river wave length is,and the smaller the flow inertia is,representing the characteristics of the “small flow”.
 |
| Fig. 14 Variations of imaginary part of char- acteristic frequency with different αf and varying " |
 |
| Fig. 15 Variations of real part of character- istic frequency with different αf and varying " |
It can be seen from Fig. 15 that,when αf = 0.03,the real part of the frequency increases continuously when the relative deviation amplitude increases; when αf = 0.2,it decreases continuously when the relative deviation amplitude increases; whereas when αf = 0.1,it increases at first,and then decreases.
(ii) Variations of neutral curve with wave number
The wave number cannot be set as αf = 0 due to the Floquet theory used in this paper. Therefore,the results when αf → 0 are taken as those when αf = 0. Figure 16 shows the neutral curves under different river wave numbers. It can be found that the variations of the neutral curves are not so regular. When the wave number increases,the neutral curve moves to the top left corner at first,then to the lower right corner,and finally arrives at the top right corner of the figure.
 |
| Fig. 16 Neutral curves with different αf |
(i) Variations of characteristic frequency of different wave numbers and wave frequencies
As mentioned above,ωg can be positive,negative,or even complex,whose sign of the real part determines the directions of the river migration.
The variations of the characteristic frequency with different river wave numbers and river wave frequencies are shown in Figs. 17 and 18,respectively. The condition of αf = 0.001 corresponds to that with a very large wave length,and the phase φ = αfx − ωgt changes little along the flow direction (the x-coordinate). Therefore,the variations of the characteristic frequency are symmetric along the ωg-axis when αf = 0.001.
 |
| Fig. 17 Variations of imaginary part of char-acteristic frequency with different αf and varying ωg |
 |
| Fig. 18 Variations of real part of character-istic frequency with different αf and varying ωg |
As shown in Figs. 7 and 8,both the imaginary parts of the characteristic frequency when αf = 0.1 and αf = 0.2 increase when the wave frequency increases,whereas the real part increases continuously when αf = 0.1,while decreases at first,and then increases when αf = 0.2.
(ii) Variations of characteristic frequency of different relative deviation amplitudes with wave frequency
The variations of the characteristic frequency with different relative deviation amplitudes and wave frequencies are shown in Figs. 19 and 20,respectively. It can be seen that the imaginary parts of the eigenvalues with different deviation amplitudes show different features. The imaginary parts of the eigenvalue with the relative deviation amplitude of 0.018 are mainly negative,and will increase when the wave frequency increases. The imaginary parts of the eigenvalue with the relative deviation amplitude of 0.036 are mainly positive,and will decrease when the wave frequency increases. In contrast,the variations of the real parts of the eigenvalues with both the relative deviation amplitude and the wave frequency are quite similar, which increase when either the wave frequency or the relative deviation amplitude increases. Moreover,the growth rate with the relative deviation amplitude of 0.036 is higher than that with the relative deviation amplitude of 0.018.
 |
| Fig. 19 Variations of imaginary part of char- acteristic frequency with different " and varying ωg |
 |
| Fig. 20 Variations of real part of character- istic frequency with different εΨ and varying ωg |
(iii) Variations of neutral curve with wave number
The self-adaptability of the river will be reflected not only in the relative deviation amplitude and the river wave length but also in the responses to the different wave frequencies. Or,we can say that the self-adaptability of the river is not just a steady process but a dynamic process. The evolutions of the relative deviation amplitude,the adaptive variation of the river wave length to the river discharge,the creeping of the river and so on all reflect the dynamic process of the self-adaptability of the river.
The comparison of the neutral curves with different river wave frequencies is shown in Fig. 21. It can be seen from the figure that,compared with the immovable river (ωg = 0.0),the rivers which can move a little (ωg = −0.01 and ωg = 0.02) are more stable. Moreover,the river, whose wave frequency ωg is −0.01,is even more stable than that whose wave frequency ωg is 0.02.
 |
| Fig. 21 Comparison of neutral curves with different ωg |
The hydrodynamic instability characteristics of the laminar flow in a narrow deep bending river are studied by use of the Floquet theory. The results are compared with those of the plane Poiseuille flow. For the convenience of calculation,a coordinate transformation is applied. To get more details from the flow near the bed,a spectral method is adopted to discretize the equation,which can give a denser distribution of the collocation points in the near bed region. The Muller method and the Q-R method are introduced to solve the equations. The obtained results are checked to ensure the validity and the accuracy of the eigenvalue. The following conclusions can be drawn:
(i) The velocity distribution of each section changes a little due to the bending. Moreover, the dynamic axis of the bending river deviates a little bit from that of the straight channel,but is within the amplitude range of the river.
(ii) The neutral curve moves to the right at first,and then moves to the left when the relative deviation amplitude εΨ increases. Moreover,the curve tends to be straight,and the critical wave number tends to decrease at first,and then increase rapidly.
(iii) The imaginary parts of the characteristic frequencies of both εΨ = 0.018 and εΨ = 0.036 show a slower decreasing tendency when the Reynolds number increases.
(iv) The real part of the characteristic frequency is closely related to both the Reynolds number and the characteristic wave number. When both the Reynolds number and the wave number increase,the frequency increases.
(v) Both the imaginary part and the real part of the frequency of the bending river with the relative deviation amplitude of 0.018 or 0.036 tend to increase at first,and then decrease rapidly.
(vi) The variations of the neutral curves are not so regular. When the wave number increases, the neutral curve moves to the top left corner at first,then moves to the lower right corner, and finally arrives at the top right corner of the figure.
(vii) The imaginary part of the eigenvalue with the relative deviation amplitude of 0.018 is mainly negative,and will increase when the wave frequency increases,whereas the imaginary part of the eigenvalue with the relative deviation amplitude of 0.036 is mainly positive,and will decrease when the wave frequency increases. In contrast,the variations of the real parts of the eigenvalues with the relative deviation amplitudes of 0.036 and 0.018 are quite similar, which increase when the wave frequency increases. Moreover,the growth rate with the relative deviation amplitude of 0.036 is higher than that with the relative deviation amplitude of 0.018.
(viii) Compared with the immovable river,the rivers which can move a little are more stable. Moreover,the river,whose wave frequency is −0.01,is even more stable than that with the wave frequency of 0.02.
The results in this paper not only can reveal the dynamic evolution characteristics of the bending river,but also can provide some references to the study of the flow drag reduction in flexible pipes.
| [1] | Frank, E. Flow and bed topography in channel bends. Journal of the Hydraulics Division, 100, 1631-1648(1974) |
| [2] | Parker, G. and Andrews, E. D. Sorting of bedload sediments by flow in meander bends. Water Resource Research, 21, 1361-1373(1985) |
| [3] | Zhao, Y. A. and Long, P. L. Channel Pattern Dynamics, Yellow River Institute of Hydraulic Research, Zhengzhou, 43-46(2005) |
| [4] | Hou, H. C. Basic Problem of River Dynamics, Water Resource Press, Beijing (1982) |
| [5] | Shao, X. J. and Wang, G. Q. The impact of upper yellow river hydropower development on downstream fluvial processes. Journal of Hydroelectric Engineering, 76, 128-138(2002) |
| [6] | Syunsuke, I., Gary, P., and Kenji, S. Bend theory of river meanders, part 1:linear development. Journal of Fluid Mechanics, 112, 363-377(1981) |
| [7] | Parker, G., Sawai, K., and Ikeda, S. Bend theory of river meanders, part 2:nonlinear deformation of finite-amplitude bends. Journal of Fluid Mechanics, 115, 303-314(1982) |
| [8] | Chang, H. H. Fluvial Processes in River Engineering, Krieger Publishing Company, New York (1988) |
| [9] | Bai, Y. C. and Luo, J. S. The loss of stability of laminar flow in open channel and the mechanism of sand ripple formation. Applied Mathematics and Mechanics (English Edition), 23(2), 276-293(2002) DOI 10.1007/BF02438335 |
| [10] | Bai, Y. C. and Xu, H. J. A study on the stability of laminar open-channel flow over a sandy rippled bed. Science in China, Series E:Engineering & Materials Science, 35, 53-73(2005) |
| [11] | Shi, X. G. Turbulence, Tianjin University Press, Tianjin (1994) |
| [12] | Bai, Y. C. and Andreas, M. A linear disturbance theory for coherent structure and mechanic sand waves in open-channel flow. International Journal of Sediment Research, 16, 234-243(2001) |
| [13] | Hou, H. C. Analysis on the dynamic process of the laminar boundary layer. Journal of Sun Yatsen University, 4, 35-52(1977) |
| [14] | Bai, Y. C. and Xu, D. Numerical simulation of the lateral migration of meandering rivers and floodplain development processes. Journal of Sediment Research, 4, 68-72(2010) |
| [15] | Yalin, M. S. River Mechanics, Pergamon Press, Oxford (1992) |
| [16] | Bai, Y. C. Nonlinear River Dynamics, Tianjin University, Tianjin (2009) |
| [17] | Monson, D. J., Seegmiller, H. L., and McConnaughey, P. K. Comparision of experiment with calculations using curvature-corrected zero and two equation turbulence models for a two-dimensional U-duct. AIAA 21st Fluid Dynamics, Plasma Dynamics and Lasers Conference, Seattle (1990) |
| [18] | Jiang, L. and Lakashminarayana, B. Prediction of strongly curved turbulent duct flows with Reynolds stress model. AIAA Journal, 35, 91-98(1997) |
| [19] | Zhang, R. J., Xie, J. H., and Chen, W. B. River Dynamics, Wuhan University Press, Wuhan (2007) |
| [20] | Zhao, G. F. Secondary instability of large scale structure in free turbulent shear layer. Applied Mathematics and Mechanics (English Edition), 16(4), 383-389(1995) DOI 10.1007/BF02456952 |
| [21] | Herbert, T. Secondary instability of boundary layers. Annual Review of Fluid Mechanics, 20, 487-526(1988) |
| [22] | Wang, F. M. Accurate solution of the Orr-Sommerfeld eigenvalue equation. Chinese Journal of Computational Physics, 2, 489-497(1985) |
| [23] | Wang, F. M. and Huang, Z. Y. An expansion solution of Orr-Sommerfeld eigenvalue problem for Poiseuille flow (in Chinese). Journal on Numerical Methods and Computer Application, 1, 37-51(1991) |
| [24] | Shen, Y. M., Wu, X. G., and Zheng, Y. H. Algebraic-stress turbulent model for 2-D plane flow in curvilinear coordinates. Journal of Hydraulic Engineering, 36, 383-390(2005) |
| [25] | Orszag, S. A. Accurate solution to the Orr-Sommerfeld stability equation. Journal of Fluid Mechanics, 50, 689-703(1971) |
| [26] | Reynolds, W. C. and Potter, M. C. Finite-amplitude instability of parallel shear flows. Journal of Fluid Mechanics, 27, 465-492(1967) |
| [27] | Nishioka, M. and Ichikawa, Y. An experimental investigation of the stability of plane Poiseuille flow. Journal of Fluid Mechanics, 72, 731-751(1975) |
 2015, Vol. 36
2015, Vol. 36















































