Shanghai University
Article Information
- Zhixin ZHAN, Weiping HU, Miao ZHANG, Qingchun MENG. 2015.
- Revised damage evolution equation for high cycle fatigue life prediction of aluminum alloy LC4 under uniaxial loading
- Appl. Math. Mech. -Engl. Ed., 36(9): 1185-1196
- http://dx.doi.org/10.1007/s10483-015-1970-6
Article History
- Received Apr. 16, 2014;
- in final form Jan. 16, 2015
2. China Academy of Space Technology, Beijing 100094, China
In the field of mechanical engineering,most structures are subject to the cyclic load,and fatigue failure is a common phenomenon,which has become an important factor related to the economy and security of structures in many engineering fields. Therefore,it is important to study the fatigue life prediction method. In engineering,considerable experimental data are needed to predict the fatigue life of components[1] . However,many problems exist in the application of this method. Thus,finding an easy method to predict the fatigue life of a structure is necessary.
In practice,many methods are adopted to predict the fatigue life of components. In the methods of stress equivalent[2] and stress invariants[3] ,the S-N curves are used to predict the fatigue life of the components. The local stress strain method[4, 5] is another method to predict the fatigue life,which is based on the stress strain course at the notch root,and is combined withthe material fatigue characteristic curve. Stanfield[6] and Stulen and Cummings[7] proposed the critical plane approach,in which the maximum value of the fatigue damage parameter was obtained among many different planes. However,this method is based on the physical observations that fatigue cracks initiate on some planes and employ some empirical equations. The mechanism of material fatigue is indefinite in the method.
For structures under variable amplitude loadings in high fatigue,the continuum damage mechanics theory is an important method for predicting the fatigue life[8, 9, 10] . When the S-N curve and external loads are known,the accuracy for the fatigue life prediction depends on the rationality of the fatigue cumulative damage criterion. Therefore,the most efficient method to predict the fatigue life is applying the continuum damage mechanics to fatigue problems and getting the reasonable damage evolution equation. In 1988,Chaboche and Lesne[11] first applied the continuum damage mechanics method to predict the fatigue life. Based on the continuum damagemechanics theory,Lemaitre and Desmorat[12] proposed several fatigue damage evolution equations.
However,there are still some problems in the applications of the prediction method based on the continuum damage mechanics theory. For example,the life prediction accuracy is related to the load values,and is not satisfactory in high cycle fatigue. Furthermore,many material parameters in the damage evolution equation are hard to be obtained. In this paper,based on the fatigue damage evolution equation of Lemaitre and Desmorat[12] ,a revised two-scale damage model is proposed according to the experimental phenomenon. Then,a method to obtain the material parameters of the revised equation from the present fatigue experimental data is proposed. Finally,a finite element model of smooth specimen is built in the ANSYS platform to calculate the fatigue life,in which the coupling effect between the fatigue damage of materials and the stress distribution in structures is taken into account. The outcome shows that the numerical prediction tallies with the experimental results,indicating that the revised damage evolution model can be applied for the fatigue life prediction in high cycle fatigue.
2 Revised two-scale fatigue damage model 2.1 Revised initial damage thresholdUnder the conditions of high cycle fatigue loading,materials generally will not enter the yield stage. Therefore,materials or structures will not produce plasticity on the macroscale,which means that no damage will appear. However,on the microscale,as long as the stress exceeds the fatigue limit,micro plasticity will be produced,resulting in the damage accumulation which can be measured by assessing whether the cumulative micro plastic von Mises strain reaches the threshold value or not. Lemaitre and Desmorat[12] gave two formulas as follows:
where p was the accumulated plastic strain,pD was the damage threshold accumulated plastic strain,εpD was the damage threshold plastic strain,σu was the ultimate stress,σf was the fatigue limit,σs was the yield stress,∆σΣ/2 was the stress amplitude,η was the hydrostatic sensitivity damage parameter,Cy was the kinematic hardening parameter,and m was the material parameter.However,some problems emerge in the application of Eq. (2). In high cycle fatigue,the stress amplitude ∆σΣ/2 is close to the fatigue limit σf . When the stress amplitude increases ordecreases slightly,the term (∆σΣ/2−σf) in Eq. (2) will change greatly,leading to a significant increase or decrease in pD. Consequently,the final predicted fatigue life will change remarkably,which obviously does not agree with the real situation. Therefore,according to the above equations,Yang et al. [13] proposed a formula as follows in order to be consistent with the experimental data:
The formula is perfectly applied to the fatigue life prediction of the aluminum alloy 2A12-T4. However,this damage evolution equation cannot be satisfactorily used to predict other high strength aluminum alloy materials such as the high strength aluminum alloy LC4.In this paper,based on the experimental data of the aluminum alloy LC4,the expression of the damage threshold accumulated plastic strain pD is revised as follows:
where m and α are material parameters. This expression reflects the following facts. First, when the stress ratio R does not change,the increase of the stress amplitude will lead to the decrease in pD. Accordingly,the fatigue life will decrease. Secondly,when the mean stress increases,the fatigue life σf with respect to the maximum stress will increase,leading to the decrease in pD. Therefore,the fatigue life will decrease.Damage will initiate after a number of cycles N0 when the damage threshold pD is reached on the microscale. There will be no micro damage as long as N < N0. Considering a periodic loading,we have
2.2 Damage extent and constitutive relationDuring the process of cyclic loading,the micro-defects in materials are generated along with the gradual degradation of the mechanical properties,followed by a failure. Based on the continuum damage theory[14, 15] ,the mechanical property deterioration can be well described.
The constitutive relation for the isotropic materials without damage on the microscale is
where σµ ij and ε µ ij stand for the stress components and the strain components on the microscale, respectively. δij and δkl are the Kronecker delta functions. λ and µ are the Lame constants defined by where E is the elastic modulus without damage,ν is the Poisson ratio,and G is the shear modulus.Assume an isotropic damage evolution for the material. Then,the stiffness deterioration can be represented by the damage variable D,which is defined by[16]
where ED is the elastic modulus with damage.Based on the isotropic damage theory,there is no relation between ν and the damage extent D. Based on Eqs. (7) and (8),the Lame constants with damages can be obtained as follows:
where λD and µD are the Lame constants with damages. According to Eqs. (6) and (9),the constitutive relation with damages on the microscale is obtained by substituting λD and µD into λ and µ,respectively[17, 18, 19] ,i.e., Under the condition of uniaxial loading,Eq. (10) is changed to 2.3 Energy release rate on microscaleFatigue failure is an irreversible thermodynamic process. According to Refs. [20]-[22],the damage strain energy release rate Y µ on the microscale can be defined by[23]
where ρ represents the medium mass density,and ψµ stands for the thermodynamic potential. During the isothermal process, where ρψµ is the free energy per unit volume,and Wµ is the strain energy density. Under the elastic loading condition,the strain energy density with damage can be expressed as follows: Then,Eq. (12) can be rewritten as follows: with where Rµ υ is the triaxiality function,σµ eq is the von Mises equivalent stress,σµ H is the hydrostatic stress,and σµD is the stress deviator. 2.4 Damage evolution equationAt the mesoscale,the proportional loading condition can be characterized by
where σij represents the stress tensor,σΣ is the signed von Mises stress,and 
In accordance with the principle of thermodynamics,the damage evolution equation can be obtained from the dissipation potential function
where λ is the plasticity multiplier,and FD represents the dissipative damage potential function expressed as where S and s are material parameters. From Eq. (21),the damage evolution law can be obtained as follows: where p represents the accumulated plastic strain rate. 2.5 Simplified damage evolution equationIn high cycle fatigue,the stress-strain curves at two scales (mesoscale and microscale) are shown in Fig. 1[12] .
 |
| Fig. 1 Stress-strain cycles at microscale and mesoscale[12] |
The thick line represents the stress-strain curve at mesoscale,which means that no macro plasticity is produced. The thin line represents the stress-strain curve at microscale. When the von Mises stress at mesoscale exceeds the value of the fatigue limit,the micro plasticity will be produced.
In the micro stress-strain cycle,when the damage is accumulated during the elastic-plastic period,Lemaitre and Desmorat[12] showed that
where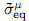 is the effective von Mises equivalent stress at microscale,and σf represents the fatigue
limit. Then,the expression of the damage evolution law can be simplified as follows:
In the upper branch of the cycle,the damage increment is
In the lower branch of the cycle,the damage increment is
Then,the damage increment over one cycle is
which can be approximated by the following equations:
where
is the effective von Mises equivalent stress at microscale,and σf represents the fatigue
limit. Then,the expression of the damage evolution law can be simplified as follows:
In the upper branch of the cycle,the damage increment is
In the lower branch of the cycle,the damage increment is
Then,the damage increment over one cycle is
which can be approximated by the following equations:
where

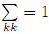 ,the damage evolution equation becomes
The number of cycles to failure ND under the cycle loading is obtained by integrating Eq. (30)
from D = 0 (the initial undamaged state) to Dc (the macrocrack initiation).
,the damage evolution equation becomes
The number of cycles to failure ND under the cycle loading is obtained by integrating Eq. (30)
from D = 0 (the initial undamaged state) to Dc (the macrocrack initiation).Therefore,the total life of the structure is the sum of life before the damage and the life during the damage,i.e.,
3 Experiments and material parameters for LC4This paper takes the high strength aluminum alloy LC4 plate as an example. The middle and high cycle fatigue experimental data of standard LC4 specimens used in this study come from the handbook[24] . The conventional properties such as E,G,εpD,and σu of LC4 can be obtained by consulting the literature. The chemical composition and the mechanics properties are presented in Tables 1 and 2[25] . Therefore,to calculate the fatigue life of structures,the four material parameters α,m,S,and s in the damage evolution equation must be determined. In the following part,the least square method is introduced to obtain the four material parameters.
Under the condition of the confirmed stress state,the smooth specimens are sustained by the uniaxial fatigue loading with the known mean stress σm and the Poisson ratio maximum nominal stress σmax,and the fatigue life nR can be obtained by consulting the S-N curve of the material. According to the damage evolution equation,the fatigue life is a function of α,m,S, and s,i.e.,
Then,we can get the optimum value via the following formula: where k is the number of the adopted data,standarding for the different stress states. We can determine the values of α,m,S,and s by setting k = 4. In theory,for the same kind of materials,the four parameters are constants. However,if different data of the S-N curve are adopted,then different values of parameters can be obtained. In the following,according to the 6 data of the S-N curve,15 groups of data are formed,and the approximate scope of the material parameters are determined. The 6 data are listed in Table 3. The optimum results of α,m,S,and s with different original data of the S-N curve are shown in Table 4. At the start of the optimization,the scopes of the parameters are set as follows:0 ≤ α ≤ 1,1 ≤ m ≤ 10,1 ≤ S ≤ 100,0.5 ≤ s ≤ 10.
According to the data listed in Table 4,we can get0.1 < α < 0.2,4.8 < m < 6.3,11.2 < S ≤ 14.3,0.9 < s < 1.4.
In practical applications,more data of the S-N curve are acquired to obtain more accurate results.According to the above optimum results,the material parameters for the LC4 alloy used in this paper are listed in Table 5.
To predict the fatigue life of components with the finite element on the ANSYS platform[26] , the ANSYS parametric design language (APDL) is applied,and the interaction effect of the damage field and the stress field is considered.
It is summarized as follows:
(i) First,all the parameters are initiated,and the calculation of the stress field is conducted.
(ii) Second,Young’s modulus E is modified to describe the material degradation according to the following equation:
(iii) By means of Eq. (31),∆ND is adopted to calculate the damage extent increment as follows:
(iv) Then,
(v) When the accumulation of damage extent at any element reaches Dc,the fatigue crack initiation life is
This is the damage mechanics finite element method to predict the fatigue life,which is also the validation method of the modified model. 4.2 Example verification of modified modelThe smooth specimen is modeled for the verification of the modified model,whose geometric profile is shown in Fig. 2.
 |
| Fig. 2 Geometric profile of model |
To eliminate the effects of the stress concentration,one half of the model is adopted along the direction of the width and thickness,and symmetry constraints are applied on the corresponding symmetry planes. The fatigue load and stress ratio are shown in Table 6. The mechanical properties of LC4 are presented in Table 1. The calculation results under different stress levels are shown in Table 6. The stress ratio is the ratio of the minimum stress and the maximum stress. Positive stress ratio means tensile stresses,while negative stress ratio means compressive stresses. Ea is the absolute value of the ratio of the difference between the numerical result and the experimental result.
Figures 3-6 compare the experimental data and the predicted S-N curves for smooth plate specimens when

 |
| Fig. 3 Experiment points and predicted S-N curve of smooth specimens when σm=0 MPa |
 |
| Fig. 4 Experiment points and predicted S-N curve of smooth specimens when σm=70 MPa |
 |
| Fig. 5 Experiment points and predicted S-N curve of smooth specimens when σm=140 MPa |
 |
| Fig. 6 Experiment points and predicted S-N curve of smooth specimens when σm=210 MPa |
From the comparisons between the experimental results and the numerical results,we can see that,within the wide range of the stress ratio [−1,0.5],the maximum error of the experimental results and the numerical results is about 36%,and the average error is about 17%. The computational accuracy is good for the fatigue calculation,which means that the revised damage evolution model can be applied for the prediction of the fatigue life in high cycle fatigue.
5 Conclusions(i) Based on the fatigue damage evolution equation of Lemaitre and Desmorat[12] ,considering practical applications,the expression of the initial damage threshold value is revised. According to the experimental data of the high strength aluminum alloy LC4,the fatigue damage evolution parameters are fitted,and the value ranges of the parameters are determined.
(ii) According to the characteristics of fatigue problems,the finite element method of damage mechanics is implemented by use of the APDL language to predict the fatigue life of standard smooth specimens. The coupling relation between the damage field and the stress field is considered in this method. The calculated fatigue lives of the smooth specimens are in good agreement with the experimental results,proving that the revised two-scale damage evolution equation can be successfully used for the high cycle fatigue life prediction of the aluminum alloy LC4 under uniaxial loading.
| [1] | Schijve, J. Fatigue of Structures and Materials, Kluwer Academic, Dordrecht, 1-5(2001) |
| [2] | Gonçalves, C. A., Araújo, J. A., and Mamiya, E. N. Multiaxial fatigue:a stress based criterion for hard metals. International Journal of Fatigue, 27, 177-187(2005) |
| [3] | Cristofori, A. and Tovo, R. An invariant-based approach for high-cycle fatigue calculation. Fatigue & Fracture of Engineering Materials & Structures, 32, 310-324(2009) |
| [4] | Socie, D. F. Fatigue-life prediction using local stress-strain concepts. Experimental Mechanics, 17, 50-56(1977) |
| [5] | Seshadri, R. The generalized local stress strain (GLOSS) analysis-theory and applications. Journal of Pressure Vessel Technology, 113, 219-227(1991) |
| [6] | Stanfield, G. Discussion on the strength of metals under combined alternating stresses. Proceedings of the Institution of Mechanical Engineers, 131, 93(1935) |
| [7] | Stulen, F. and Cummings, H. A failure criterion for multi-axial fatigue stresses. Proceedings of the American Society for Testing and Materials, 54, 822-835(1954) |
| [8] | Krajcinovic, D. Continuum damage mechanics. Applied Mechanics Reviews, 37, 1-6(1984) |
| [9] | Chaboche, J. L. Continuous damage mechanics-a tool to describe phenomena before crack initiation. Nuclear Engineering and Design, 64, 233-247(1981) |
| [10] | Lemaitre, J. and Chaboche, J. L. Mechanics of Solid Materials, Cambridge University Press, Cambridge, 442-449(1990) |
| [11] | Chaboche, J. and Lesne, P. A nonlinear continuous fatigue damage model. Fatigue & Fracture of Engineering Materials & Structures, 11, 1-17(1988) |
| [12] | Lemaitre, J. and Desmorat, R. Engineering Damage Mechanics:Ductile, Creep, Fatigue and Brittle Failures, Springer, Berlin, 283-288(2005) |
| [13] | Yang, F. P., Sun, Q., Luo, H. J., and Zhang, H. A corrected damage law for high cycle fatigue (in Chinese). Acta Mechanica Sinica, 44, 140-147(2012) |
| [14] | Kachanov, L. Introduction to Continuum Damage Mechanics, Springer, Berlin, 1-6(1986) |
| [15] | Bathias, C. and Pineau, A. Fatigue of Materials and Structures, Wiley Online Library, New York, 47-50(2010) |
| [16] | Murakami, S. Continuum Damage Mechanics:a Continuum Mechanics Approach to the Analysis of Damage and Fracture, Springer, Berlin, 19-22(2012) |
| [17] | Argente dos Santos, H. A. F., Auricchio, F., and Conti, M. Fatigue life assessment of cardiovascular balloon-expandable stents:a two-scale plasticity-damage model approach. Journal of the Mechanical Behavior of Biomedical Materials, 15, 78-92(2012) |
| [18] | Desmorat, R., Kane, A., Seyedi, M., and Sermage, J. P. Two scale damage model and related numerical issues for thermo-mechanical high cycle fatigue. European Journal of Mechanics, A:Solids, 26, 909-935(2007) |
| [19] | Lautrou, N., Thevenet, D., and Cognard, J. Y. Fatigue crack initiation life estimation in a steel welded joint by the use of a two-scale damage model. Fatigue & Fracture of Engineering Materials & Structures, 32, 403-417(2009) |
| [20] | Zhang, X. Fracture and Damage Mechanics (in Chinese), Beijing University of Aeronautics and Astronautics Press, Beijing, 327-331(2006) |
| [21] | Hansen, N. and Schreyer, H. A thermodynamically consistent framework for theories of elastoplasticity coupled with damage. International Journal of Solids and Structures, 31, 359-389(1994) |
| [22] | Chaboche, J. L. Thermodynamic formulation of constitutive equations and application to the viscoplasticity and viscoelasticity of metals and polymers. International Journal of Solids and Structures, 34, 2239-2254(1997) |
| [23] | Lemaitre, J., Sermage, J., and Desmorat, R. A two scale damage concept applied to fatigue. International Journal of Fracture, 97, 67-81(1999) |
| [24] | Wu, X. R. Handbook of Mechanical Properties of Aircraft Structural Metals (in Chinese), Aviation Industry Press, Beijing, 222-225(1998) |
| [25] | Gao, Z. T. The Fatigue Performance Experiments Design and Data Processing (in Chinese), Beijing University of Aeronautics and Astronautics Press, Beijing (1999) |
| [26] | Zhang, M., Meng, Q. C., Hu, W. P., Shi, S. D., Hu, M., and Zhang, X. Damage mechanics method for fatigue life prediction of pitch-change-link. International Journal of Fatigue, 32, 1683-1688(2010) |
 2015, Vol. 36
2015, Vol. 36















































