1 Introduction

It is well-known that the interface equations play an important role in material sciences and fluid dynamics when two or more distinct materials or fluids with different conductivities, densities,or diffusions are involved^{[1, 2, 3]} . Because of the irregular geometry of the interface and the low global regularity of the exact solutions,it is very diffcult to achieve the well- pleasing accuracy of the numerical methods. The immersed finite element method (IFEM)^{[4, 5, 6]} is one of the effcient methods to conquer the above diffculties caused by the interface,whose key component is to construct a proper immersed finite element (FE) space according to the interface jump conditions near the interface. In this case,much inconvenience during the scientific calculations will be brought out by the stiffness matrix of the immersed FE space, which is completely different from that of the noninterface FE space.

Recently,Chen and Zou^[7] proposed a simple P₁-conforming triangular FEM to solve the interface problems,and obtained the suboptimal order error estimates in the H₁-norm and the L²-norm when the interface was of the C²-smooth. Moreover,Chen and Zou^[7] pointed out that the error estimate in the H₁-norm could reach optimal if the exact solution belonged to W^1,∞ near the interface. Later,Sinha and Deka^[8] provided the detailed proof of the above statement,and Sinha and Deka^[9] extended this method to semi-linear cases.

However,the works mentioned above are mainly contributions to the conforming FEs. In fact,nonconforming FEs have many advantages comparing with conforming FEs^{[10, 11, 12, 13]} . The unknowns of the elements are associated with the element edges or faces,and each degree offreedom belongs to at most two elements. Therefore,the use of nonconforming elements facili- tates the exchange of information across each subdomain,and provides spectral radius estimates for the iterative domain decomposition operator^[14] . As an attempt,in this paper,we adopt the lowest order P₁-nonconforming triangular FE to deal with linearly elliptic and parabolic interface problems,and derive the optimal order error estimates with the same assumptions as those in Refs. ^[8] and ^[9] on the exact solution. Finally,we give some numerical results to verify the theoretical analysis.

2 Elliptic interface problem

Let Ω be a convex polygon in R²,Ω⁻ ⊂ Ω be an open domain with a C² curve bound Γ ⊂ Ω, Let Ω be a convex polygon in R²,Ω⁻ ⊂ Ω be an open domain with a C² curve bound Γ ⊂ Ω, Let Ω be a convex polygon in R²,Ω⁻ ⊂ Ω be an open domain with a C² curve bound Γ ⊂ Ω, and Ω⁺ = Ω \ Ω^- (see Fig. 1). We consider the following elliptic interface problem: find

such that where the jump conditions on the interface Γ are

In (2),we denote by [v]Γ the jump of a quantity v across the interface Γ,and denote by n the unit outward normal to Γ. The coeffcient β is a positive piecewise constant function defined by

where

Similar to Ref. ^[8],we assume that Ω₀ is some neighborhood of the interface Γ,and

To describe the triangulation T_h = {K} of the domain Ω,we first approximate the domain Ω^- by the domain Ω^- _h with a polygonal boundary Γ_h whose vertices all lie on the interface Γ. Then,

Each K ∈ T_h satisfies the following conditions:

(i) K is either in Ω^- _h or Ω⁺ _h .

(ii) If F is an edge of K,then F has either vertices or the whole edge lying on Γ when

K is called an interface element if it is intersected by Γ; otherwise,K is called a noninterface element. We denote the diameter of K by hK,satisfying

For convenience,we write the set of the interface elements as T * _h ,and let h be small enough such that

For each K ∈ T * _h ,let

Since the interface Γ is of the C²-smooth,we know either

or

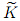Throughout this paper,we will use to denote one of the two subregions K⁻ and K⁺,which satisfies

where c is a generic positive constant independent of h,but may take different values at different appearances.

The lowest order P₁-nonconforming triangular FE space is defined by

where P₁(K) is the polynomial space of degree 1,and [v]F equals v itself while F ⊂ ∂Ω.

Let Π_h : H₁(Ω) → V_h be the associated interpolation operator on V_h,and Π_h|K = Π_K, satisfying

where F₁,F₂,and F₃ are the three edges of K. Then,the corresponding variational form of (1) can be written as follows: find u ∈ H¹₀ (Ω) such that and the jump conditions in (2) are satisfied,where

The corresponding P₁-nonconforming FE discrete form of (6) reads: find u_h ∈ V_h such that

where

and β_h = β^s if K ⊂ Ωs h.

Obviously,if we choose V_h = u_h in (7),then

where ||v_h||_h is a broken energy norm on V_h defined by

3 Error estimates for elliptic interface problem

In order to derive the error estimates for the problem (1),we need to prove the following lemmas.

Lemma 1 For all

we have where

Proof If K is a noninterface element,by the standard interpolation theory^[15] ,we have

Else,if K ∈ T * _h is an interface element,and without lose of generality,let

we have

Since

letting p → ∞ in (11) yields Combining (10) and (12) completes the proof.

Lemma 2 Let K be a general element with three edges F_i (i = 1,2,3),and

Then,for u ∈ X(K) and v_h ∈ V_h,we have

Proof If K is a noninterface element,then the desired results can be found in Ref. ^[13]. Therefore,we only need to prove the case K ∈ T * _h . Without loss of generality,let

First,by the trace theorem,we can obtain

Second,let be the restriction of on K⁻. Because the function continues across Γ,we can extend the function onto the whole element K,and obtain a function such that^[5]

Therefore,we can derive that

The proof is completed.

Lemma 3 For u ∈ X(Ω) and v_h ∈ V_h,we have

Proof Since continues across ∂K,and

we have Then,applying Lemma 2 to (15) leads to the desired result.

Theorem 1 Let u and u_h be the solutions of (1) and (7),respectively. Then,we have

Proof Subtracting (6) from (7) and noticing a_h(u − Π_hu,v_h) = 0,we can obtain

First,from Lemma 3,we have

Second,noticing the difference between β and β_h,since (∇u_h)|K and (∇v_h)|K are constants, we have

Here,the inequality (8) has been used in the last step.

Thus,choosing v_h = u_h − Π_hu in (17),we have

The desired result follows from Lemma 1 and the triangle inequality.

Theorem 2 Under the assumptions of Theorem 1,we have

Proof Consider the following auxiliary problem:

with the jump conditions From Ref. ^[7],(19) has a unique solution w satisfying

Therefore,

which leads to the desired result.

4 Parabolic interface problem

In this section,we consider the fully-discrete FE scheme of the parabolic interface problem, and derive the optimal order error estimate.

Let Ω be the domain described in Section 2,and

We consider the following parabolic interface problem: where the solution u(x,t) satisfies the jump conditions in (2),and u0(x) ∈ H₁ 0 (Ω) is the initial condition.

The corresponding weak form of (21) is to find

such that

Assume that [0,T] is divided into N parts equally by

Let

Then,the fully-discrete FE scheme of (22) is where u^h _n denotes the FE solution at t = t_n,and

Theorem 3 Let

be the solutions of (21) and (23) at t = t_n,respectively. Then,we have

Proof For convenience,we introduce the following symbols:

It can be checked that

Subtracting (23) from (22) at t = t_n+1 and taking v_h = η_n+1 yield

Since

the above equation turns to

Moreover,since

letting

we have

which implies Summating (26) from n = 0 to L − 1 (1≤L≤N) yields

By use of the fact

from the Gronwall lemma in Ref. ^[16],we obtain The above equation together with Lemma 1 yields the desired result.

5 Numerical results

In this section,we present some numerical results for the interface problems in the domain Ω = ^{[0, 2]} × ^{[0, 1]}. The interface Γ occurs at x₁ = 1.

First,we can obtain the rectangular meshes with m divisions along the x₁-axis and l divisions along the x₂-axis. Second,we separate each small rectangle to two triangles by the diagonal line. The triangular subdivision is thus completed. Now,we give two numerical examples for elliptic and parabolic interface problems,respectively.

Example 1 Elliptic interface problems

The corresponding right-hand term of (1) is taken as follows:

The exact solution u can be expressed as follows: If we choose

where k is an odd number,and β⁺ = 1,then the jump conditions

are satisfied.

The errors are listed in Table 1 for k = 3 and Table 2 for k = 7,respectively. Moreover, we plot the convergence rates of the L²-norm in Fig. 2 and the broken energy norm in Fig. 3, respectively. Example 2 Parabolic interface problems In (21),let

and the corresponding right-hand term be as follows: The exact solution u can be expressed as follows:

The errors are listed in Tables 3-6 when

where

It can be seen from Tables 1-6 and Figs. 2-3 that the numerical results coincide with our theoretical analysis,and the proposed method can achieve very good performance for interface problems.

6 Conclusions

In this paper,we discuss the P₁-nonconforming triangular FEM for interface problems. We should mention that (∇v_h)|K = constant for all v_h ∈ V_h is essential in the above analysis. Therefore,the method cannot be used to other very popular nonconforming FEs^{[11, 17, 18, 19, 20]} .

Moreover,we point out that this method is also suitable for second-order semi-linear elliptic interface problems with a little modification of the estimates. However,how to use the proposed method to nonlinear cases still remains open.