Shanghai University
Article Information
- Minwei CHEN, Min LI, Xuesong TANG. 2015.
- Moving line crack accompanied with damage zone subject to remote tensile loading
- Appl. Math. Mech. -Engl. Ed., 36(9): 1213-1222
- http://dx.doi.org/10.1007/s10483-015-1975-6
Article History
- Received Sept. 8, 2014;
- in final form Jan. 26, 2015
2. Department of Mechanics, School of Civil Engineering and Architecture, Changsha University of Science & Technology, Changsha 410004, China
The investigation of moving crack problems not only is of theoretical significance,but also has practical applications. The mechanical behavior of moving crack tips is similar to the mechanical behavior of dynamic crack propagation. Yoffe[1] got the earliest analytical solution for the moving Griffith crack model,in which the crack moved at a constant speed. This analytical solution is called as Yoffe’s solution. Moving cracks have been widely studied in recent years. Hu and Li [2] investigated the constantly moving crack in a magnetoelectroelastic material under anti-plane shear loading. Hermann et al. [3] studied a moving interface crack with a contact zone in a piezoelectric bimaterial. Lapusta et al. [4] analyzed the limited permeable crack moving along the interface of a piezoelectric bimaterial. Hu et al. [5] studied a moving crack in a rectangular magnetoelectroelastic body. Xie and Liu[6] investigated the cracking characteristics of a moving screw dislocation near an interfacial crack in two dissimilar orthotropic media. Sih and Jones[7] studied the crack size and speed interaction characteristics at micro-,meso-and macro-scales. Tang and Sih[8] studied the kinetics of the microcrack blunting ahead of the macrocrack approaching the shear wave speed.
The speed of the crack in moving crack problems is generally limited down to the Rayleigh wave speed because of the mathematical difficulties. However,the speed of the moving crack may not only reach the Rayleigh wave speed but also reach the transcend shear wave speed[9] . This paper introduces a restraining stress zone,where the distribution and magnitude of the restraining stresses are connected with the moving speed and damage degree of the crack tip material. The concept of restraining stress zone was proposed by Sih and Tang[10] . After that, they set up many multiscale crack models based on the restraining stress zone and uniform model of multiscale fatigue crack growth[11, 12, 13, 14, 15, 16] . After the restraining stress zone is brought in, the crack opening displacement (COD) is continuous not only under the Rayleigh wave speed but also under the shear wave speed.
2 Concept and analysis model of restraining stress zoneThe concept of the restraining stress zone is illustrated in Fig. 1. A uniaxial tension plate, which has no damage,is shown in Fig. 1(a). It is assumed that an incision with the length 2a is cut in the plate. Therefore,restraining stresses occur along the incision (see Fig. 1(b)). Figure 1(c) presents a crack with the length 2a. If σ0 = σ∞,the material has no damage. If σ0 = 0,the material is entirely damaged. When 0 < σ0 < σ∞,the material is partly damaged. Therefore,the restraining stress zone can describe the material damage.
 |
| Fig. 1 Concept of restraining stress zone |
Suppose that there is a crack at a velocity v in an infinite plate (see Fig. 2). σ* ∞ is the applied uniform tensile stress. (x1,x2) is the fixed coordinate system. (ζ,η) is the moving coordinate system,moving together with the crack,which can be described as follows:
Consider that the material at the crack tip has some damages. The damage zone at the tip is described by a restraining stress zone. The distribution of the restraining stresses is R(χ). The distribution function R(χ) depends on the damages of the material at the tip and the moving velocity. A linear distribution of the restraining stresses is considered as follows: where f(v) is a function related to the velocity,while a1 and a2 are both constants,which determine the distribution condition of the restraining stresses. In addition,a position function should be defined to confirm the restraining stresses of each point at the restraining zone,i.e., If the stresses σc at χ = c,σp,and p are known,the restraining stresses at each point can be determined. |
| Fig. 2 Moving crack model with restraining stress zone |
If the body forces are not considered,we can transform the two-dimensional elastic dynamic governing equation into the Navier equation as follows:
where λ and µ are the Lame constants. ui is the displacement,and ρ is the density. A(x1,x2,t) and B(x1,x2,t) are the potential functions of the volume deformation and the shear deformation, respectively. The displacement can be shown as follows: Then,Eq. (4) can be rewritten as follows: where ∇2 is the Laplace operator. Sd is the dilatational wave speed. Ss is the shear wave speed. E is the elastic modulus. ν is the Poisson ratio.Substitute the moving coordinate system into Eq. (1). Then,Eq. (6) can be rewritten as follows:
Introduce the complex variables zd and zs as follows:
Then,the two displacement potential functions F(zd) and G(zs) can be written as follows: Therefore,the solutions of the displacements and stresses can be given by[17] As a result,the key to determine the two analytic functions is the boundary conditions. 4 Stress intensity factor (SIF) and COD solutionsAs shown in Fig. 2,the results that the applied stresses and restraining stresses applied to the plate are equal to the superpositions of the two applied stresses. The subscript “σ” indicates that the applied stresses are applied independently,and the subscript “r” means that the restraining stresses are applied independently. The solution that the applied uniform stresses σ* ∞ are applied independently is the Yoffe solution[1] ,i.e. [17]
For the moving crack problem,σ* ∞ is related to the crack speed. It can be assumed that In view of Eq. (17),D is the function of the speed v. When v = SR and D = 0,the Rayleigh wave speed formula can be obtained as follows:In the following description,the result,where the restraining stresses are applied alone, is considered. Figure 3 shows the resultant force R(χ)dχ. The distribution forces at the symmetrical positions are regarded as the concentrated forces. Two pairs of concentrated forces are symmetrically applied to the moving crack surfaces. The solution of the analytic function is[7]
Inserting Eq. (2) into Eq. (21) and integrating the obtained result from a to c,the solution under the restraining stresses acting on the crack surfaces can be rewritten as follows: Substituting Eq. (22) into Eq. (23) yields The result of the combined action is given by the superposition of the applied stresses and restraining stresses,i.e., It is shown in the classic fracture mechanics that the stress singularity can be produced only at the crack tip. In order to get the size of the restraining zone,the stress singularity condition must take the advantage at ζ = c. Therefore,the two SIFs must be satisfied by Substituting Eqs. (18) and (24) into Eq. (27) yields Note that c = a + b and the size b of the crack tip of the damage zone can be determined. |
| Fig. 3 Two pairs of concentrated forces symmetrically applied to moving crack surfaces |
The COD denoted by δ is defined by
Substituting Eqs. (12),(16),(25),and (26) into Eq. (29) yields
5 Normalized strain energy density (SED)The SED function is denoted by dW/dV . It is a positive function,which is used to analyze the behavior of the static and moving crack from the macroscopic perspectives. It can also explain the multiscale condition[7] . The SED at the crack tip can be written as follows[18, 19]
where σ11,σ22,and σ12 can be confirmed by Eqs. (13),(14),and (15).For discussion convenience,we introduce a normalized SED defined by
to replace the previous SED. 6 Numerical results and discussionSuppose that the material is the magnesium alloy MB15,which is widely used in the space navigation structure. The material parameters are displayed as follows:

When it satisfies


 |
| Fig. 4 Normalized COD at middle point versus normalized crack moving speed curves |
The two velocity functions g(v) and f(v) are introduced to solve the above problems. The two velocity functions g(v) and f(v) are introduced to solve the above problems. According to Ref. [8],the two velocity functions can be written as follows:
Assume that the restraining stresses are triangularly distributed. Then,the relevant parameters can be given by The restraining stresses are zero at χ = a while σ0 at χ = c. In terms of Eq. (28),the length b of the restraining stress zone has nothing to do with the velocity v,but depends on the ratio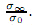 . The numerical results are shown in Table 1. It is shown that the damage zone of the crack
tip increases when the imposed loads increase.
. The numerical results are shown in Table 1. It is shown that the damage zone of the crack
tip increases when the imposed loads increase.When v = 0,(1 − αs2 )/D in Eq. (30) has the form of 0/0. Then,from L’Hospital’s rule,we can obtain
When v = SR,f(v)/D in Eq. (30) also becomes 0/0. Then,from L’Hospital’s rule in the same way,we can obtain It is seen that the COD is continuous and finite while v = SR after introducing the velocity function f(v). In Fig. 5,it is verified that the COD is continuous when the moving speed increases from 0 to the shear wave speed Ss,especially spanning the Rayleigh wave speed. In terms of Fig. 5,it is found that the COD decreases when the moving speed increases. |
| Fig. 5 Normalized COD versus normalized moving speed curves for different lo- cations |
Figure 6 indicates that the COD curves at the middle point vary with the moving speed. The COD enlarges obviously with the increase in the load. Figure 7 gives the changing curves of the COD with the abscissa for different moving speeds,while Fig. 8 describes the changing curves of the COD with the abscissa for different stresses,which reflects that the COD and the damage length of the crack tip tend to increase sharply in the stresses.
 |
| Fig. 6 Normalized COD at middle point versus normalized moving speed curves for dif- ferent stress ratios |
 |
| Fig. 7 Normalized COD versus normalized coordinate ζ/α for different moving speeds |
 |
| Fig. 8 Normalized COD versus normalized co- ordinate ζ/α for different stress ratios |
In the process of the researching SED,the propagation at the tip of the restraining stress zone is concerned. As a result,the normalized coordinate ζ/a turns into ζ/c. Figures 9 and 10 depict that the normalized SED decreases when the normalized coordinate increases for v/SR = 0.5 and v/SR = 1.0,respectively. Moreover,the normalized SED curves slightly vibrate at the stretch of 1.0 < ζ/c < 1.03. The reason is that the places approaching the tip of the restraining stress zone have a significant effect on the SED. The curves in Fig. 9 are sparse,while the curves in Fig. 10 are compact,which explains the reduced effect of the SED on the moving speed.
 |
| Fig. 9 Normalized SED versus normalized coordinate ζ/c for different stress ra- tios for v/SR = 0.5 |
 |
| Fig. 10 Normalized SED versus normalized co- ordinate ζ/c for different stress ratios for v/SR = 1.0 |
The studies on moving crack problems take the advantage of the restraining stress zone to analyze the damage zone of the crack tip. It is assumed that the restraining stresses are linearly distributed. This paper obtains the numerical solution of the length of the damage zone in the crack tip and crack surface opening displacement by means of complex function methods.
The COD in the Dugdale moving crack model is unbounded when the moving speed equals the Rayleigh wave speed. By introducing two velocity functions,the COD becomes continuous when the crack speed steps over the Rayleigh wave speed and the shear wave speed from 0.
The numerical results manifest that the length of the damage zone in the crack tip and COD increases when the applied stresses increase,while decreases when the crack moving speed increases. Similar trends are reflected in researching the SED.
| [1] | Yoffe, E. Y. The moving Griffith crack. Philosophical Magazine, 42, 739-750(1951) |
| [2] | Hu, K. Q. and Li, G. Q. Constant moving crack in a magnetoelectroelastic material under anti-plane shear loading. International Journal of Solids and Structures, 42, 2823-2835(2005) |
| [3] | Hermann, K. P., Komarov, A. V., and Loboda, V. V. On a moving interface crack with a contact zone in a piezoelectric bimaterial. International Journal of Solids and Structures, 42, 4555-4573(2005) |
| [4] | Lapusta, Y., Komarov, A. F., Labesse-Jied, R., and Moutou-Pitti, V. L. Limited permeable crack moving along the interface of a piezoelectric bi-material. European Journal of Mechanics, A:Solids, 30, 639-649(2011) |
| [5] | Hu, K. Q., Kang, Y. L., and Qin, Q. H. A moving crack in a rectangular magnetoelectroelastic body. Engineering Fracture Mechanics, 74, 751-770(2007) |
| [6] | Xie, C. and Liu, Y. W. Cracking characteristics of a moving screw dislocation near an interfacial crack in two dissimilar orthotropic media. Theoretical and Applied Fracture Mechanics, 50, 214219(2008) |
| [7] | Sih, G. C. and Jones, R. Crack size and speed interaction characteristics at micro-, mesoand macro-scales. Theoretical and Applied Fracture Mechanics, 39, 127-136(2003) |
| [8] | Tang, X. S. and Sih, G. C. Kinetics of microcrack blunting ahead of macrocrack approaching shear wave speed. Theoretical and Applied Fracture Mechanics, 42, 99-130(2004) |
| [9] | Rosakis, A. J., Samudrala, O., and Coker, D. Cracks faster than the shear wave speed. Science, 284, 1337-1340(1999) |
| [10] | Sih, G. C. and Tang, X. S. Dual scaling damage model associated with weak singularity for macro-scopic crack possessing a micro-/meso-scopic notch tip. Theoretical and Applied Fracture Mechanics, 42, 1-24(2004) |
| [11] | Tang, X. S. and Sih, G. C. Weak and strong singularities reflecting multiscale damage:micro-boundary conditions for free-free, fixed-fixed and free-fixed constraints. Theoretical and Applied Fracture Mechanics, 43, 5-62(2005) |
| [12] | Sih, G. C. and Tang, X. S. Screw dislocations generated from crack tip of self-consistent and self-equilibrated systems of residual stresses:atomic, meso and micro. Theoretical and Applied Fracture Mechanics, 43, 261-307(2005) |
| [13] | Tang, X. S. and Sih, G. C. Edge dislocations generated from a microcrack under initial residual stress of non-uniform distribution. Theoretical and Applied Fracture Mechanics, 44, 208-233(2005) |
| [14] | Sih, G. C. and Tang, X. S. Triple scale segmentation of non-equilibrium system simulated by macro-micro-atomic line model with mesoscopic transitions. Theoretical and Applied Fracture Mechanics, 44, 116-145(2005) |
| [15] | Tang, X. S. and Sih, G. C. Equilibrium mechanics model of multiscaling by segmentation:asymptotic solution for macro-meso-micro damage in anti-plane shear deformation. Theoretical and Applied Fracture Mechanics, 44, 1-15(2005) |
| [16] | Tang, X. S. Scatter of fatigue data owing to material microscopic effects. Science China, Series G:Physics, Mechanics and Astronomy, 57, 90-97(2004) |
| [17] | Freund, L. B. Dynamic Fracture Mechanics, Cambridge University Press, London (1990) |
| [18] | Sih, G. C. Dynamic crack problems:strain energy density fracture theory. Mechanics of Fracture-Elastodynamic Crack Problem, Noordhoff International Publishing, Leyden (1976) |
| [19] | Sih, G. C. Mechanics of Fracture Initiation and Propagation, Kluwer Academic Publishers, Boston (1991) |
 2015, Vol. 36
2015, Vol. 36










































