Shanghai University
Article Information
- A. K. VASHISHTH, A. DAHIYA, V. GUPTA. 2015.
- Generalized Bleustein-Gulyaev type waves in layered porous piezoceramic structure
- Appl. Math. Mech. -Engl. Ed., 36(9): 1223-1242
- http://dx.doi.org/10.1007/s10483-015-1976-6
Article History
- Received Sept. 8, 2014;
- in final form Jan. 23, 2015
Piezoelectric materials are the materials which can produce an electric field when they are deformed and undergo deformation subjected to an electric field. Piezoelectric materials can be applied in various functional devices such as sensors,actuators,filters,and delay lines,which are widely used in electronic technology,mechanical engineering,and medical appliance. The wave propagation in piezoelectric structures has received considerable attention[1, 2, 3, 4] .
The shear-horizontal (SH) type acoustic wave is the wave where the particle displacement lies in the propagation surface and is perpendicular to the wave propagation direction. The shear waves propagating in a piezoelectric medium are important in the surface acoustic wave (SAW) analysis. SAW devices are of great interest for chemical and biochemical sensing applications because of their high sensitivity to the mass loading on the surface. A number of problems have been studied for the SH wave propagation in piezoelectric structures. Feng and Li [5] de- rived the existence condition for the SH waves in a layered structure of piezoelectric ceramics, and discussed the propagation characteristics of the waves. Mesquida et al. [6, 7] analyzed the propagation characteristics of the waves in functionally graded piezoelectric material (FGPM)composite structures. Romeo[8] studied the inter-facial waves occurring at the separation sur- face between two piezoelectric dispersive media. Qian et al. [9] investigated the propagation behavior of the shear waves in multi-layered piezoelectric composite structures. Li et al. [10] investigated the localization of the SH waves in disordered periodic layered piezoelectric struc- tures,considering the electromechanical coupling. Qian et al. [11] investigated the existence and propagation behavior of the transverse surface wave in a layered structure consisting of a piezoelectric substrate and a gradient metal layer,and used the Wentzel-Kramers-Brillouin method to obtain the analytic solutions in the gradient metal layer. Qian et al. [12] and Du et al. [13] investigated the existence and propagation of the transverse surface waves in piezoelectric coupled solids.
Bleustein[14] and Gulyaev[15] simultaneously discovered that there existed a shear horizon- tal electro-acoustic surface mode in a class of transversely isotropic piezoelectric media,which was known as the Bleustein-Gulyaev (B-G) wave. The B-G wave theory has become one of the cornerstones for modern electro-acoustic technology. The surface electro-acoustic waves in multi-layered media are of practical importance in signal transmission,signal processing,and information storage applications. From the view point of device applications,surface waves are advantageous over bulk waves because they are relatively easy to be excited and to be detected. Bright and Hunt[16] studied the B-G waves in several cubic piezoelectric semiconductors of the cubic class,and developed the data for the velocity,coupling factor,and penetration depth. Li [17] obtained the exact solutions of a shear horizontal electromagneto-acoustic surface wave mode in a class of 6mm piezoelectric media. Yang[18] investigated the propagation character- istics of the B-G wave for the SAW device application. Jin et al. [19] investigated the layered structure with films and substrates made of the same piezoelectric material but having oppo- site poling directions,and found that the B-G wave could propagate in the structure and its penetration depth was on the same order as the wavelength. Zhang et al. [20] investigated theB-G wave for liquid sensing applications,and found that the B-G wave did not radiate energy into the contacting liquid and was sensitive to the changes of the liquid density and viscosity. Yang[21] studied the propagation of the B-G wave in ceramics under finite biasing mechani- cal fields. Jin and Wang[22] and Liu et al. [23] discussed the effects of the initial stress on the phase velocity of the B-G wave and the corresponding electro-mechanical coupling factor in the layered piezoelectric structures. Kielczynski et al. [24] used the perturbation theory to measure the shear modulus and viscosity of the B-G wave. Guo and Sun[25] investigated the B-G wave propagation in the half-space piezoelectric materials loaded with viscous liquid. Cao et al. [26] investigated the problem of the B-G wave propagation in a functionally graded piezoelectric material (FGPM) layer/transversely isotropic piezoelectric substrate composite system,and used the technique of power series to solve the governing equations. Li et al. [27] investigated the B-G waves in a functionally graded transversely isotropic electro-magneto-elastic half-space, where all parameters exponentially changed along the depth direction. Daros[28] investigated the B-G wave in a specific class of functionally graded materials,and used the Liouville-Green approximation for the second-order matrix differential equations with explicit computable error bounds. Yu et al. [29] used a double orthogonal polynomial series approach to solve the wave propagation problem in the piezoelectric-piezomagnetic multilayered structure. Abdalla and Asker[30] studied the propagation of the surface B-G wave in a piezoelectric layered half-space.
However,due to the brittle nature of piezoelectric ceramics and the possible defects of impu- rity,cavities,and microcracks,failures of devices take place easily under mechanical or electrical loading. In order to overcome these disadvantages,porosity is added to piezoelectric materi- als,resulting in porous piezoelectric materials,which have more applications in comparison with dense piezoelectric materials. Porous piezoelectric structures have been studied only by a few scientists. Gupta and Venkatesh[31] developed a finite element model to study the ef- fect of porosity on the electro-mechanical response of porous piezoelectric ceramics. Vashishth and Gupta[32] derived constitutive equations for porous piezoelectric materials. Vashishth and Gupta[33] studied the wave propagation in transversely isotropic porous piezoelectric materi- als. Vashishth and Gupta[34] proved the uniqueness theorem and the theorem of reciprocity for porous piezoelectric materials under the assumption of positive definiteness of elastic and electric fields. Vashishth and Dahiya[35] studied the propagation of the SH type wave in a com- posite structure consisting of alternating polymeric layers and porous piezoelectric layers,and discussed the dispersion and the stop-pass band behavior of the Floquet wave. The problem of the B-G type waves in porous piezoelectric materials has not been studied so far.
In the present paper,the propagation of the B-G type wave in a piezoceramic layered struc- ture consisting of multiple layers and a half-space of porous piezoelectric media with different polarization is studied. The dispersion equations,by using the transfer matrix method,are obtained for both electrically shorted and open boundaries. It is further studied in this paper that,for a layered media consisting of a single porous piezoelectric layer and a half-space,hav- ing the same polarization but different in nature,a peculiar kind of B-G waves can propagate in the structure.
2 Formulation of problemA model is considered (see Fig. 1). It consists of n porous piezoelectric layers with the thickness hi over the porous piezoelectric half-space.
 |
| Fig. 1 Layered porous pizeoelectric structure |
The layers and the half-space are considered to be transversely isotropic,having the same axis of symmetry but opposite polarization directions. The propagation is considered in the xy-plane. The poling direction of the layers is the same as the positive direction of the z-axis, while the poling direction of the half-space is opposite to the former. The total thickness of the layers is h,and the surface x = 0 is the free surface. The constitutive equations for the porous piezoelectric materials are as follows[32] :
where σij(σ*) and εij(ε*) are the stress and the strain tensor for the solid (fluid) phase in the porous piezoelectric material,respectively. Di(D* i ) and Ei(E* i ) are the electric displace- ment and the electric field vector for the solid (fluid) phase in porous piezoelectric material, respectively. cijkl ,mij ,and R are the elastic constants. eijk,e* i ,ζijk,and ˜ζi are the piezoelec- tric constants,and ξij ,ξ* ij ,and Aij are the dielectric constants. The equations of motion for porous piezoelectric materials in the absence of the body forces and surface charge density are as follows: where ui and U* i are the mechanical displacement components corresponding to the solid phase and the fluid phase of the porous aggregate,respectively. (ρ11)ij ,(ρ12)ij ,and (ρ22)ij are the dynamical mass coeffcients.Moreover,we have
where φ (φ*) is the electric potential for the solid (fluid) phase.The mechanical displacement and the electric potentials,representing the motion of the B-G waves,can be written as follows:
Substituting Eqs. (1),(3),and (4) into Eq. (2) yields
where 
The layers and the half-space are transversely isotropic porous piezoelectric media but with opposite polarization. Therefore,we have
where the superscript “a” is used for the layers,and the superscript “s” is used for the half- space. From Eqs. (7) and (8),we can obtain the equations of Eqs. (5) and (6) corresponding to the layers as follows: and the equations of Eqs. (5) and (6) corresponding to the half-space as follows: where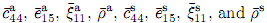 are given in Appendix A.
are given in Appendix A.Usually,the medium above the layer is considered as air. However,the dielectric constants of air are very small in comparison with those of the porous piezoelectric materials. Therefore, the space above the layer can be treated as vacuum. If the electric potential and the dielectric constant in air are represented as φ°(x,y,t) and ε°,respectively,then
The electric displacement (D°) in air is defined by 3 Solutions of problemFor the porous piezoelectric layered structures,the solution of Eq. (9) is assumed as follows:
where k is the wave number,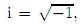 c is the propagation velocity of the B-G waves,and
Wa(x),Φa(x),and Φ*a(x) are undetermined functions.
c is the propagation velocity of the B-G waves,and
Wa(x),Φa(x),and Φ*a(x) are undetermined functions.Making use of Eqs. (9) and (13) and simplifying them thereafter,we get
where 
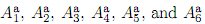 are undetermined coeffcients.
are undetermined coeffcients.Following the same procedure for the porous piezoelectric half-space,we have
where 
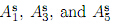 are undetermined coeffcients. It is noted that
are undetermined coeffcients. It is noted that

The solutions for the air/vacuum are
where A° is the undetermined coeffcient,and the radiation condition 
Equation (14) at the surface x = hi (i = 1,2,3,… … … ,n) can be rewritten as follows:
where 


Then,Eq. (17) can be rewritten as
where 1≤i≤n,and Ti is the local transfer matrix whose elements are given in Appendix A.Using the above procedure for each layer and following the continuity of the field components at the layer interfaces,we can finally relate the displacements and the stresses at the upper surface of the layered structure,i.e.,x = 0,to those at the lower surface,i.e.,x = h,via the individual transfer matrix multiplication

Then,Eq. (15) at the surface x = h can be written as follows:
where 

At x = h,


The boundary conditions at x = 0,when it is electrically open boundary,are
Substituting Eqs. (16) and (21) into Eq. (22) yields 
The existence condition of the non-trivial solution of this homogeneous system leads to
which is the dispersive equation for the open case,and ε°,G11,G12,G13,G21,G22,and G23 are given in Appendix A.In the case when a single layer is considered over the porous piezoelectric half-space and the layer and the half-space have the same material constants but opposite polarization,Eq. (23) can be reduced to
where εr,K1,L1,L2,and L3 are given in Appendix B. 5.2 Electrically shorted caseThe boundary conditions at x = 0,where the boundary is shorted,are
Substituting Eqs. (16) and (21) into Eq. (25) yields 
The dispersive equation can be written as follows:
In the case when a single layer is considered over the porous piezoelectric half-space and the layer and the half-space have the same material constants but opposite polarization,Eq. (26) can be reduced to
5.3 Reduced caseIn this sub-section,the dispersion equations (24) and (27) are reduced for the piezoelectric case. For the open case,if


Consider the same assumptions. Then,Eq. (27) for the electrically shorted case can be reduced to
which is the dispersion equation of the B-G wave in the layered piezoelectric half-space for the electrically shorted case obtained by Jin et al. [19] . 6 Numerical examples and discussionThe dispersion equations of the B-G wave are derived for both electrically open and elec- trically shorted cases in the previous section. For the numerical computation,the materials PZT-1 and PZT-5H are used as the porous piezoelectric layers,and the material PZT-7 is used as the porous piezoelectric half-space. The values of the material parameters used in the com- putation are listed in Table 1. The phase velocities of the B-G wave for the electrically open and electrically shorted cases are denoted by co and cs,respectively. The electromechanical coupling factor for the surface wave is related to the effciency of a transducer in the converting electrical to mechanical energy and vice-versa,and is defined by
The variations of the phase velocity of the B-G wave for the electrically open case and the electrically shorted case with the dimensionless thickness h/λ,where λ is the characteristic wavelength,of the layers in the layered structure are shown in Figs. 2 and 3,respectively. The first,second,third,and fourth layers are considered as PZT-1,PZT-5H,PZT-1,and PZT- 5H,respectively. The half-space is considered as PZT-7. This stack is denoted by 1-5-1-5-7. Similarly,1-5-7 represents two layers of PZT-1 and PZT-5H over a half-space of PZT-7. Thecase of a single layer (PZT-1) over a half-space (PZT-7) is denoted by 1-7. From Figs. 2 and 3, it is observed that when the total thickness of the layers increases,the phase velocity decreases rapidly first,and then increases slightly. For a fixed dimensionless thickness,the value of the phase velocity for the electrically open case is larger than that for the case of the shorted boundary. When the number of the layers increases in the layered structure,the effects on the phase velocity of the B-G wave are very small.
 |
| Fig. 2 Variations of phase velocity (co) with dimensionless thickness (h/λ) of lay-ers for electrically open case |
 |
| Fig. 3 Variations of phase velocity (cs) with dimensionless thickness (h/λ) of lay-ers for electrically shorted case |
The variations of the electromechanical coupling factor on the surface ( ) with the dimen-
sionless thickness are shown in Fig. 4. When the thickness is very small,i.e.,h/λ = 0.01,the
value of
) with the dimen-
sionless thickness are shown in Fig. 4. When the thickness is very small,i.e.,h/λ = 0.01,the
value of  is 7.1%. However,when the thickness increases from 0.01 to 0.1,
is 7.1%. However,when the thickness increases from 0.01 to 0.1, decreases first,
and then starts increasing thereafter. Therefore,for the appropriate thickness of the layers,the
coupling factor
decreases first,
and then starts increasing thereafter. Therefore,for the appropriate thickness of the layers,the
coupling factor  can still maintain quite high values.
can still maintain quite high values.
 |
Fig. 4 Variations of electromechanical coupling factor ( ) with dimensionless thickness (h/λ) ) with dimensionless thickness (h/λ) |
The effects of the porosity in the layered structure,consisting of a single layer and a half-space of the identical material PZT-1,on the phase velocity and the coupling factor at the surface for the electrically open case and the electrically shorted case are shown in Figs. 5 and 6,respec- tively. From Fig. 5,it can be seen that for both the electrically open case and the electrically shorted case,the phase velocity of the B-G wave increases due to the porosity in the piezoelectric materials. It can also been observed that the coupling factor decreases due to the porosity in thepiezoelectric layered structure when the upper fluid half-space is dielectric in nature (see Fig. 6). If the upper half-space is not dielectric,i.e.,the upper surface of the porous piezoelectric layered structure is free,then the coupling factor increases in the porous piezoelectric layered structure in comparison with that of the piezoelectric layered structure. Therefore,the boundary condi- tions at the upper surface of the layered structure determine the coupling factor. The porous piezoelectric layered structure is of great importance for the SAW devices in comparison with that for the piezoelectric layered structure if the upper half-space is not dielectric.
 |
| Fig. 5 Variations of phase velocity with dimensionless thickness (h/λ) for piezoelectric and porous piezoelec-tric materials (PZT.1) for electrically open and shorted cases |
 |
Fig. 6 Variations of electromechanical cou-
pling factor  with dimension-less thickness (h/λ) for piezoelec-tric and porous piezoelectric materi-als (PZT.1) with dimension-less thickness (h/λ) for piezoelec-tric and porous piezoelectric materi-als (PZT.1) |
A peculiar kind of modes for the B-G wave can be achieved when the constants of the mate- rials satisfy a certain relationship. For this case,a piezoceramic layered structure is considered, consisting of a layer and a half-space. The polarization directions of the layer and the half-space are taken along the z-axis.
The boundary conditions at the surface x = 0 are the same as Eq. (22) or (25). At the interface x = h,the boundary conditions ensure the continuity of the normal components of the stress,displacements,electrical potential function,and electrical displacements. In addition to these boundary conditions,the following condition,which assures the propagation of the peculiar B-G wave,must be satisfied:
The phase velocity equation of the peculiar electro-acoustic wave,that can be propagated in the porous piezoelectric layered structure for the electrically open case,can be obtained as follows: where 
For the electrically shorted case,the phase velocity equation is given by
where 
In the case of the peculiar B-G wave,the porous piezoelectric layered structure case can be reduced to the piezoelectric layered structure case when

Then,Eq. (32) can be reduced to the dispersion equation as follows:
which is the phase velocity equation for the peculiar B-G wave for the piezoelectric layered structure for the electrically open case given by Jin et al. [19] .In the electrically shorted case,Eq. (33) reduces to
which is the phase velocity equation for the peculiar B-G wave for the piezoelectric layered structure given by Jin et al. [19] for the electrically open case.The phase velocity can be computed easily if the material constants of the layer and the half-space,the thickness of the layer,and the interface parameters are known. When some ofthe material constants are pre-determined,the other parameters can be detected theoretically. The pre-determined parameters are

The numerical results are shown in Figs. 7-13 by taking PZT-1 as the layer and PZT-5H as the half-space.
 |
| Fig. 7 Relation between β and co for α = 0.5 (electrically open case) |
The variations of β and α with the phase velocity for different h/λ are shown in Figs. 7 and 8 for the electrically open case and in Figs. 9 and 70 for the electrically shorted case,respectively. From the above figures,we can see that,for a fixed phase velocity,when h/λ increases,both α and β decrease. For a fixed h/λ,α and β decrease linearly when the phase velocity increases for both the electrically open case and the electrically shorted case.
 |
| Fig. 8 Relation between α and co for β = −10 (electrically open case) |
 |
| Fig. 9 Relation between β and cs for α = 0.5 (electrically shorted case) |
 |
| Fig. 10 Relation between α and cs for β = −8 (electrically shorted case) |
 |
| Fig. 11 Relation between β and α for electrically open and shorted cases where co,cs = 1 000m·s−1 |
The behaviors of β with α for different h/λ are shown in Fig. 11 for the electrically open case and the electrically shorted case. For a fixed h/λ,β decreases steadily when α increases. When h/λ increases,β decreases for a fixed α for both the electrically open case and the electrically shorted case. It can be seen from the computed results that β<0 holds under all circumstances, which indicates that the polarization of the layer and the half-space must be opposite to each other. The relations between β and α with the phase velocity cs are shown in Figs. 12 and 13 for h/λ = 0.5 in the cases of piezoelectric and porous piezoelectric media,respectively. In Fig. 12,it is clear seen that,when the phase velocity is less than 1 030m·s−1,β is small for a porous piezoelectric medium in comparison with that for a piezoelectric medium,while this observation is reversed when the phase velocity exceeds 1 030m·s−1. This observation is also noticed in Fig. 13 where cs = 1 014.5m·s−1.
 |
| Fig. 12 Relation between β and cs for piezoelectric and porous piezoelec- tric materials (electrically shorted case) when α = 0.5 |
 |
| Fig. 13 Relation between α and cs for piezoelectric and porous piezoelec- tric materials (electrically shorted case) when β = −8 |
The B-G type surface waves in a layered poro-piezoelectric structure are studied. The dispersion relation for the existence of such surface waves is studied in a simple mathematical form. The modes of propagation,which exist in the electrically open case and the electrically shorted case,are investigated. The high values of the electromechanical coupling factor can be obtained for a suitable choice of the thickness of the layer. The phase velocity of the B-G type wave increases when the porosity increases. This factor may be of importance in enhancing the performance of the SAW devices based on the B-G type surface waves. The existence of this peculiar kind of propagation modes of B-G waves,which depends on the choices of the material constants and the thickness of layer,is also studied. Two parameters are chosen for this case,and the polarization directions of the layer and the half-space are opposite to each other. The results obtained in the present study are validated by obtaining the previously established results as the particular cases.
| [1] | Cady, W. G. Piezoelectricity, McGraw-Hill, NewYork (1946) |
| [2] | Auld, B. A. Acoustic Fields and Waves in Solids I, Wiley, New York (1973) |
| [3] | Auld, B. A. Acoustic Fields and Waves in Solids II, Wiley, New York (1973) |
| [4] | Nayfeh, A. H. Wave Propagation in Layered Anisotropic Media, Elsevier, Amsterdam (1995) |
| [5] | Feng, H. and Li, X. Shear-horizontal surface waves in a layered structure of piezoelectric ceramics. IEEE Transactions on Ultrasonićs, Ferroelectrics, and Frequency Control, 40, 167-170(1993) |
| [6] | Mesquida, A. A., Otero, J. A., Ramos, R. R., and Comas, F. G. Wave propagation in layered piezoelectric structures. Journal of Applied Physics, 83, 4652-4659(1998) |
| [7] | Mesquida, A. A., Ramos, R. R., Comas, F. G., Monsivais, G., and Sirvent, R. E. Scattering of shear horizontal piezoelectric waves in piezocomposite media. Journal of Applied Physics, 89, 2886-2892(2001) |
| [8] | Romeo, M. Electromagnetoelastic waves at piezoelectric interfaces. International Journal of Engineering Science, 42, 753-768(2004) |
| [9] | Qian, Z., Jin, F., Kishimoto, K., andWang, Z. Effect of initial stress on the propagation behavior of SH-waves in multilayered piezoelectric composite structures. Sensors and Actuators, A:Physical, 112, 368-375(2004) |
| [10] | Li, F., Wang, Y., Hu, C., and Huang, W. Wave localization in randomly disordered periodic layered piezoelectric structures. Acta Mechanica Sinica, 22, 559-567(2006) |
| [11] | Qian, Z. H., Jin, F., Lu, T., and Hirose, S. Transverse surface wave in a piezoelectric material carrying a gradient metal layer of finite thickness. International Journal of Engineering Science, 47, 1049-1054(2009) |
| [12] | Qian, Z., Jin, F., and Hirose, S. A novel type of transverse surface wave propagating in a layered structure consisting of a piezoelectric layer attached to an elastic half-space. Acta Mechanica Sinica, 26, 417-423(2010) |
| [13] | Du, J., Xian, K., Yong, Y. K., and Wang, J. SH-SAW propagation in layered functionally graded piezoelectric material structures loaded with viscous liquid. Acta Mechanica, 212, 271-281(2010) |
| [14] | Bleustein, J. L. A new surface wave in piezoelectric material. Applied Physics Letters, 13, 412-413(1968) |
| [15] | Gulyaev, Y. V. Electroacoustic surface waves in solids. Journal of Experimental and Theoretical Physics Letters, 9, 37-38(1969) |
| [16] | Bright, V. M. and Hunt,W. D. Bleustein-Gulyaev waves in gallium arsenide and other piezoelectric cubic crystals. Journal of Applied Physics, 66, 1556-1564(1989) |
| [17] | Li, S. The electromagneto-acoustic surface wave in a piezoelectric medium:the Bleustein-Gulyaev mode. Journal of Applied Physics, 80, 5264-5269(1996) |
| [18] | Yang, J. S. Bleustein-Gulyaev waves in piezoelectromagnetic materials. International Journal of Applied Electromagnetic and Mechanics, 12, 235-240(2000) |
| [19] | Jin, F., Wang, Z. K., andWang, T. J. The Bleustein-Gulyaev (B-G) wave in a piezoelectric layered half-space. International Journal of Engineering Science, 39, 1271-1285(2001) |
| [20] | Zhang, C., Caron, J. J., and Vetelino, J. F. The Bleustein-Gulyaev wave for liquid sensing applications. Sensors and Actuators, A:Physical, 76, 64-68(2001) |
| [21] | Yang, J. S. Bleustein-Gulyaev waves in strained piezoelectric ceramics. Mechanics Research Communications, 28, 679-683(2001) |
| [22] | Jin, F. andWang, Z. The propagation behavior of Bleustein-Gulyaev waves in a pre-stressed piezoelectric layered structure. International Journal of Nonlinear Sciences and Numerical Simulation, 4, 125-138(2003) |
| [23] | Liu, H., Kuang, Z. B., and Cai, Z. M. Propagation of Bleustein-Gulyaev waves in a prestressed layered piezoelectric structure. Ultrasonics, 41, 397-405(2003) |
| [24] | Kielczynski, P., Pajewski, W., Szalewski, M., and Balcerzak, A. Measurement of the shear storage modulus and viscosity of liquids using the Bleustein-Gulyaev wave. Review of Scientific Instruments, 75, 2362-2367(2004) |
| [25] | Guo, F. L. and Sun, R. Propagation of Bleustein-Gulyaev wave in 6 mm piezoelectric materials loaded with viscous liquid. International Journal of Solid and Structure, 45, 3699-3710(2008) |
| [26] | Cao, X., Jin, F., Wang, Z., and Lu, T. Bleustein-Gulyaev waves in a functionally graded piezoelectric material layered structure. Science China, Series G:Physics, Mechanics and Astronomy, 52, 613-625(2009) |
| [27] | Li, P., Jin, F., and Qian, Z. Propagation of the Bleustein-Gulyaev waves in a functionally graded transversely isotropic electro-magneto-elastic half-space. European Journal of Mechanics, A:Solids, 37, 17-23(2013) |
| [28] | Daros, C. H. Liouville-Green approximation for Bleustein-Gulyaev waves in functionally graded materials. European Journal of Mechanics, A:Solids, 38, 129-137(2013) |
| [29] | Yu, J. G., Lefebvre, J. E., and Zhang, C. Guided wave in multilayered piezoelectric-piezomagnetic bars with rectangular cross-sections. Composite Structures, 116, 336-345(2014) |
| [30] | Abdalla, A. and Asker, N. Numerical simulations for the phase velocities and the electromechanical coupling factor of the Bleustein-Gulyaev waves in some piezoelectric smart materials. Mathematics and Mechanics of Solids (2014) DOI 10.1177/1081286514527861 |
| [31] | Gupta, R. K. and Venkatesh, T. A. Electromechanical response of porous piezoelectric materials. Acta Materialia, 54, 4063-4078(2006) |
| [32] | Vashishth, A. K. and Gupta, V. Vibrations of porous piezoelectric ceramic plate. Journal of Sound and Vibration, 325, 781-797(2009) |
| [33] | Vashishth, A. K. and Gupta, V. Wave propagation in transversely isotropic porous piezoelectric materials. International Journal of Solid and Structure, 46, 3620-3632(2009) |
| [34] | Vashishth, A. K. and Gupta, V. Uniqueness theorem, theorem of reciprocity, and eigenvalue problems in linear theory of porous piezoelectricity. Applied Mathematics and Mechanics (English Edition), 32(4), 479-494(2011) DOI 10.1007/s10483-011-1432-8 |
| [35] | Vashishth, A. K. and Dahiya, A. Shear waves in a piezoceramic layered structure. Acta Mechanica, 224, 727-744(2013) |
 2015, Vol. 36
2015, Vol. 36






































