Shanghai University
Article Information
- M. FAROOQ, A. ALSAEDI, T. HAYAT. 2015.
- Note on characteristics of homogeneous-heterogeneous reaction in flow of Jeffrey fluid
- Appl. Math. Mech. -Engl. Ed., 36(10): 1319-1328
- http://dx.doi.org/10.1007/s10483-015-1981-9
Article History
- Received Oct. 16, 2014
- Revised Feb. 8, 2015
2. Nonlinear Analysis and Applied Mathematics(NAAM) Research Group, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia
Materials obeying Newton's law of viscosity are known as the viscous fluids.There is a direct and linear relationship of such fluids between the shear stress and the shear strain rate (i.e.,the Hookian relationship).There are several materials (such as yoghurt,pasta,ketchup,shampoo,certain oils,mud,paints,blood at low shear rate,clay coatings,polymer melts,and greases) which have nonlinear relationship between the shear stress and the rate of strain.These materials are characterized as non-Newtonian fluids.The flows of non-Newtonian fluids in recent times have wide coverage in polymer devolatisation,fermentation,bubble absorptions,composite processing,boiling,bubble columns,plastic foam processing,and several others.Further,the flows of non-Newtonian fluids induced by a moving surface occur in paper production,plastic films,polymer extru sion,extrusion of plastic sheets,food processing,etc.Hence,the analysis of non-Newtonian fluids at present has received interest of scientists and researchers (both experimentalists and theoreticians).Such fluids vary in nature,and their constitutive equations take different forms (see[1, 2, 3, 4, 5]and several references therein).
In nature,there exist a large number of chemical reactions which have important applications.Some of the reactions proceed very slowly or do not react at all in the absence of a catalyst.The interaction between the homogeneous and heterogeneous chemical reactions is very intricate involving different rates of the chemical species of production and consumption both on the catalyst surface and within the fluid.Many chemical reactions such as combustion,catalysis,and biomedical systems consist of homogeneous and heterogeneous reactions simultaneously.Reactions such as propane oxidation over platinum and methane/ammonia have great significance in the chemical industry[6, 7].Chaudhary and Merkin[8]discussed the homogeneousheterogeneous effects in the forced convection stagnation point flow of viscous fluid.Khan and Pop[9]analyzed such effects in the viscous flow in the region of stagnation point on an infinite permeable wall.To the best knowledge of these authors,there is no attempt yet for predicting the characteristics of homogeneous-heterogeneous reaction in flows of non-Newtonian fluids.Hence,the objective here is to fill such void.Therefore,the present analysis is prepared to analyze the homogeneous-heterogeneous reaction effects in the two-dimensional boundary layer flow of a Jeffrey fluid induced by a stretching surface.The homogeneous-heterogeneous reaction is considered subject to the same reactant and auto catalyst diffusion coefficients.The governing momentum and concentration equations are modeled.The exact solution for the velocity is presented.The series solution for the concentration equation is given by the homotopy analysis method (HAM)[10, 11, 12, 13, 14, 15].The convergent series solution for the concentration equation is also examined.The variation of different parameters on the physical quantities is analyzed.
2 Mathematical formulationLet us investigate the incompressible two-dimensional boundary layer flow of a Jeffrey fluid induced by an impermeable stretching sheet.Here,we consider the homogeneous-heterogeneous reaction model proposed in Ref.[8].A Cartesian coordinate system is selected in a way that the x-axis is parallel to the stretching sheet while the y-axis is in the normal direction to the sheet.The heat released by the reaction is assumed negligible.The homogeneous reaction for the cubic autocatalysis can be represented as follows:
where r denotes the rate,while an isothermal and first-order reaction on the catalyst surface is taken in the form of In the above expressions,a and b denote the concentrations of the chemical species A and B,while k1 and ks denote the rate constants.These equations ensure that there exists no reaction rate both at the boundary layer outer edge and in the external flow region.The relevant equations through the aforementioned assumptions are where u and v represent the components of velocity along the x-and y-axes,respectively,λ1 represents the retardation time,λ2 represents the ratio of the relaxation time to the retardation time,ν represents the kinematic viscosity,and DA and DB are the diffusion coefficients of the species A and B,respectively.The applied boundary conditions are defined as follows: in which Uw and a0 are the constants. Substituting into Eqs. (4)-(7),we get where f is the dimensionless stream function,β is the material parameter,K is the strength of the homogeneous reaction measurement,Sc represents the Schmidt number,δ represents the diffusion coefficients ratio,Ks represents the strength of the heterogeneous reaction measurement,and Re represents the Reynolds number.The definitions of these quantities are The exact solution of Eq. (9) subject to the relevant conditions is[16] with It is often the case that the diffusion coefficients of chemical species A and B have the same value.This argument facilitates us to take the diffusion coefficients DA and DB as the same,i.e.,δ=1 and thus Now,Eqs. (10) and (11) yield with the boundary conditions 3 Solution procedureThe initial guess g0 and the auxiliary linear operator in the HAM solutions are chosen in the following forms:
with where Ci (i=1,2) are the arbitrary constants.If p ∈[0, 1]represents the embedding parameter,then  g represents the non-zero auxiliary parameter.The zeroth-order deformation problem is
g represents the non-zero auxiliary parameter.The zeroth-order deformation problem is
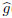 (η;p) goes from the initial solution g0(η) to the final solution g(η).Using the Taylor series expansion,we can write
The auxiliary parameters are so properly chosen that the series (28) converge at p = 1 and thus
The mth-order deformation problems are given by
The general solution of Eqs. (30)-(32) is
in which gm*(η) denotes the special solution.
4 Convergence analysis
(η;p) goes from the initial solution g0(η) to the final solution g(η).Using the Taylor series expansion,we can write
The auxiliary parameters are so properly chosen that the series (28) converge at p = 1 and thus
The mth-order deformation problems are given by
The general solution of Eqs. (30)-(32) is
in which gm*(η) denotes the special solution.
4 Convergence analysis
Obviously,the homotopy solutions contain the auxiliary parameter ( g).The series solution convergence of the problem depends upon the auxiliary parameter.To verify the convergence region,we sketch the
g).The series solution convergence of the problem depends upon the auxiliary parameter.To verify the convergence region,we sketch the  -curve for the series solution (see Fig. 1).The admissible value of
-curve for the series solution (see Fig. 1).The admissible value of  g through Fig. 1 is −2.3≤
g through Fig. 1 is −2.3≤ g≤−0.6.
g≤−0.6.
 |
Fig. 1  -curve for function g when Sc=1,K=0.4,λ2=1.0,Ks=0.4,and β=1.0 -curve for function g when Sc=1,K=0.4,λ2=1.0,Ks=0.4,and β=1.0 |
We also compute the solution of nonlinear ordinary differential equation (19) by the MATHEMATICA package BVPh 2.0 using the boundary condition (20).We find the minimum squared residual error 2.010 75× 10−9 for the concentration profile (g(η)) at the 20th-order of approximations.Fig 2 is plotted for the solution of concentration profile.The total residual error corresponding to different orders of approximations is displayed in Fig. 3.It is noted that the error decreases when the order of approximation increases.
 |
| Fig. 2 Solution curve for g(η) |
 |
| Fig. 3 Total error vs. order of approximations |
Now,we analyze the graphical results of various pertinent parameters on the axial velocity and concentration fields.The behavior of λ2 on the axial velocity distribution is shown in Fig. 4.The velocity is found to decrease when λ2 increases.The behavior of the Deborah number (β) on the axial velocity field is displayed in Fig. 5.Here,we observe that the axial velocity field and the associated thickness of the boundary layer increase when the Deborah number is increased.The characteristics of strength of the homogeneous reaction K on the concentration distribution is sketched in Fig. 6.Higher values of the strength of homogeneous reaction K result in the reduction of the concentration distribution.The variation in the strength of the heterogeneous reaction Ks on the concentration field is plotted in Fig. 7.Here,we can see that the concentration field enhances for larger Ks.The influence of the Schmidt number Sc on the concentration field is sketched in Fig. 8.Higher values of the Schmidt number result in the enhancement of the concentration distribution.The characteristics of the strength of homogeneous reaction K and λ2 on g'(0) are shown in Fig. 9.It is revealed that g'(0) decreases when the strengths of the homogeneous reaction K and the heterogeneous reaction Ks are increased.The behavior of the heterogeneous reaction Ks and the Schmidt number Sc on g(0) is shown in Fig. 10.Here,g(0) enhances for higher values of the Schmidt number Sc.Further,it is noted that g(0) has small values with the enhancement of the strength of heterogeneous reaction Ks.Figure 11 displays g(0) for the effects of the Schmidt number Sc and the homogeneous reaction K.It is concluded that g(0) shows the increasing behavior for higher values of the Schmidt number Sc.However,g(0) decreases by increasing K.
 |
| Fig. 4 Effect of λ2 on f(y) for β = 2.0 |
 |
| Fig. 5 Effect of β on f(y) for λ2 = 5.0 |
 |
| Fig. 6 Effect of K on g(η) for λ2 = 1.0, Sc =1.0, β = 0.2, and Ks = 1.0 |
 |
| Fig. 7 Effect of Ks on g(η) for λ2 = 0.5, Sc =1.0, β = 0.5, and K = 5.0 |
 |
| Fig. 8 Effect of Sc on g (η) for λ2=1.0,K=1.0,β=0.2,and Ks=1.0 |
 |
| Fig. 9 Effect of Ks and K on g'(0) for Sc=1.0,λ2=1.0,and β=1.0 |
 |
| Fig. 10 Effect of Sc and Ks on g (0) for K=2.0,λ2=0.5,and β=0.2 |
 |
| Fig. 11 Effect of Sc and K on g (0) for Ks=1.0,λ2=0.5,and β=0.2 |
Table 1 presents the series solution convergence.Here,we conclude that the series solution converges at the 34th-order of approximations for g'(0).
 |
We examine the characteristics of homogeneous-heterogeneous reaction in the twodimensional flow of Jeffrey fluid induced by an impermeable stretching sheet.The behaviors of various pertinent parameters are discussed and analyzed through graphs.The following conclusions can be made through the analysis of the graphs.
(i) The characteristics of the Deborah number (or the material parameter)β and λ2 on the axial velocity distribution are opposite.
(ii) The concentration distribution decreases with an increase in the strength of the homogeneous reaction K.
(iii) The effect of the strength of heterogeneous reaction Ks on the concentration profile is opposite to that of the strength of homogeneous reaction.
(iv) The value of concentration profile enhances for larger values of the Schmidt number.
(v) The value of g(0) increases by increasing the Schmidt number Sc whereas a reverse trend is seen for increasing K and Ks.
Acknowledgements The authors are grateful for the comments of reviewers.| [1] | Shehzad, S. A., Alsaedi, A., and Hayat, T. Hydromagnetic steady flow of Maxwell fluid over a bidirectional stretching surface with prescribed surface temperature and prescribed surface heat flux. PLOS ONE, 8, e68139(2013) |
| [2] | Li, C., Zheng, L., Zhang, Y., Ma, L., and Zhang, X. Helical flows of a heated generalized Oldroyd-B fluid subject to a time-dependent shear stress in porous medium. Communications in Nonlinear Science and Numerical Simulation, 17, 5026-5041(2012) |
| [3] | Liu, Y., Zheng, L., and Zhang, X. MHD flow and heat transfer of a generalized Burgers' fluid due to an exponential accelerating plate with the effect of radiation. Computers and Mathematics with Applications, 62, 3123-3131(2011) |
| [4] | Mukhopadhyay, S. Heat transfer analysis of the unsteady flow of a Maxwell fluid over a stretching surface in the presence of a heat source/sink. Chinese Physics Letter, 29, 054703(2012) |
| [5] | Niu, J., Fu, C., and Tan, W. Slip-flow and heat transfer of a non-Newtonian nanofluid in a microtube. PLOS ONE, 7, e37274(2012) |
| [6] | Williams, W. R., Zhao, J., and Schmidt, L. D. Ignition and extinction of surface and homogeneous oxidation of NH3 and CH4. American Institute of Chemical Engineers Journal, 37, 641-649(1991) |
| [7] | Song, X.,Williams, W. R., Schmidt, L. D., and Aris, R. Bifurcation behaviour in homogeneousheterogeneous combusion, II, computations for stagnation-point flow. Combust Flame, 84, 292-311(1991) |
| [8] | Chaudhary, M. A. and Merkin, J. H. A simple isothermal model for homogeneous-heterogeneous reactions in boundary layer flow, I. equal diffusivities. Fluid Dynamics Research, 16, 311-333(1995) |
| [9] | Khan, W. A. and Pop, I. Flow near the two-dimensional stagnation point on an infinite permeable wall with a homogeneous-heterogeneous reaction. Communications in Nonlinear Science and Numerical Simulation, 15, 3435-3443(2010) |
| [10] | Liao, S. Homotopy Analysis Method in Nonlinear Differential Equations, Springer & Higher Education Press, Berlin (2012) |
| [11] | Maleki, M., Tonekaboni, S. A. M., and Abbasbandy, S. A homotopy analysis solution to large deformation of beams under static arbitrary distributed load. Applied Mathematical Modelling, 38, 355-368(2014) |
| [12] | Si, X. H., Zheng, L. C., Zhang, X. X., and Si, X. Y. Homotopy analysis method for the asymmetric laminar flow and heat transfer of viscous fluid between contracting rotating disks. Applied Mathematical Modelling, 36, 1806-1820(2012) |
| [13] | Hayat, T., Awais, M., and Obaidat, S. Three-dimensional flow of a Jeffery fluid over a linearly stretching sheet. Communications in Nonlinear Science and Numerical Simulation, 17, 699-707(2012) |
| [14] | Rashidi, M. M., Beg, O. A., Rastegari, M. T., and Mehmood, A. Homotopy study of buoyancyinduced flow of non-Newtonian fluids over a non-isothermal surface in a porous medium. International Journal of Applied Mathematics and Mechanics, 8, 34-52(2012) |
| [15] | Turkyilmazoglu, M. Solution of the Thomas-Fermi equation with a convergent approach. Communications in Nonlinear Science and Numerical Simulation, 17, 4097-4103(2012) |
| [16] | Alsaedi, A., Iqbal, Z., Mustafa, M., and Hayat, T. Exact solutions for the magnetohydrodynamic flow of a Jeffery fluid with convective boundary conditions and chemical reaction. Zeitschrift für Naturforschung A, 67, 517-524(2012) |
 2015, Vol. 36
2015, Vol. 36























