Shanghai University
Article Information
- Ming XU, Xiaoling JIN, Yong WANG, Zhilong HUANG. 2015.
- Optimal bounded control for maximizing reliability of Duhem hysteretic systems
- Appl. Math. Mech. -Engl. Ed., 36(10): 1337-1346
- http://dx.doi.org/10.1007/s10483-015-1986-9
Article History
- Received Sept. 28, 2014;
- Revised Feb. 13, 2015
2. Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, China
Many structural components,such as passive vibration absorber and piezoelectric ceramics,exhibit hysteresis.Many civil and mechanical engineering structures equipped with these components show hysteretic behaviors under serious time-varying loading,such as typhoon,earthquake,and high-intensity noise[1, 2].The hysteretic restoring force is determined by both the instantaneous and past states of the deformation,and a hysteretic loop can be created between the hysteretic restoring force and the displacement under periodic movement.Many kinds of mathematical models have been proposed to characterize the relationship of the hysteretic force and the displacement,including the bi-linear model,the Ramberg-Osgood model,Iwan's distributed element model,Ozdemir's model,and so on[3, 4, 5, 6, 7].In all these hysteretic models,the Duhem differential model[8, 9, 10]is versatile to cover most existing hysteresis models and can describe the hysteretic behavior more accurately.
Various stochastic optimal control strategies have been proposed[11, 12, 13].However,in mechanical and structural engineering fields,only the linear quadratic Gaussian (LQG) control strategy has been widely applied.In the past decade,an optimal control strategy[14]for nonlinear systems has been developed for the quasi Hamiltonian random system with external and/or parametric excitations by Zhu et al.[15].The strategy has been applied to semi-active control,bounded control,and robust control for uncertain systems[16].The LQG control strategy is usually used to reduce the system response or to enhance the system stability,while the optimal control strategy for stochastic systems can also be used to maximize the system reliability,i.e.,minimize the first-passage failure[17].The reliability is described by the probability of the structure in the safety domain during a specified time interval.The bigger the probability is,the better the system reliability is.The design of the optimal control strategy is aimed to enhancing the reliability and making the system safer,i.e.,searching the optimal control to enlarge the probability in the safety domain.Almost all the works,however,concentrate on the non-hysteretic systems,and the only work on maximizing the reliability of hysteretic systems is contributed to the Bouc-Wen system[18].
In the present study,the process of deriving the optimal feedback control in order to maximize the reliability of the Duhem system is given.The Duhem hysteretic model is briefly presented.The controlled hysteretic system is transformed to the controlled nonlinear system without hysteresis,and then the controlled system energy's Itô differential equation is deduced according to the theorem of stochastic averaging.The dynamical programming equations with the corresponding solution conditions for the control problem of maximizing system reliability are formulated based on the dynamical programming principle.Finally,the conditional reliability functions and the mean time of the first-passage failure are obtained from the Kolmogorov equation.A tall building,which is simplified as an equivalent single-degree-of freedom system subjected to non-white noise excitations,is discussed to validate the procedures'efficacy.
2 Duhem hysteretic model The Duhem model for hysteresis satisfies the following equations:where z and x denote the hysteretic force and the displacement,respectively,and g1 and g2 are continuous functions.According to the Duhem model (1a) and (1b),the hysteretic force is determined by g1 for  > 0 and g2 for
> 0 and g2 for  < 0.The corresponding hysteresis loop in the xz-plane consists of two parts,i.e.,the ascending line z1(x) for
< 0.The corresponding hysteresis loop in the xz-plane consists of two parts,i.e.,the ascending line z1(x) for  > 0 and the descending line z2(x) for
> 0 and the descending line z2(x) for  < 0.Both the ascending line and the descending line are independent of the magnitude of velocity
< 0.Both the ascending line and the descending line are independent of the magnitude of velocity  .The hysteretic force on the ascending line or the descending line is determined by the instantaneous system state,and the local history due to the last changes in the velocity direction is independent of the displacement history before the change.Thus,the Duhem hysteresis model has the characteristics of local memory.
.The hysteretic force on the ascending line or the descending line is determined by the instantaneous system state,and the local history due to the last changes in the velocity direction is independent of the displacement history before the change.Thus,the Duhem hysteresis model has the characteristics of local memory.
For anti-symmetric Duhem hysteresis models (as shown in Fig. 1),g2(x,z)=g1(−x,−z),z1(x)=−z2(−x),a1=a2,and x10=x20=x0.In this case,the hysteretic force can be replaced by an elastic part and an inelastic part,i.e.,z1(x)=ze+zp 1,and z2(x)=ze+zp 2,in which the superscripts e and p denote elastic part and inelastic part,respectively.The potential energy can be represented as
he area of the hysteresis loop Ar represents the dissipated energy in one cycle by the hysteresis component,which can be written as |
| Fig. 1 Representative of Duhem hysteresis loop |
Discuss a one-degree-of-freedom Duhem hysteretic system subjected to random excitations and control.The equation is
where X,ζ,and Z denote the system displacement,the damping coefficient,and the Duhem hysteretic restoring force,respectively,fj (X,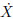 ) represent the amplitudes of external and/or parametric random excitations,which are continuous and differentiable functions of the displacement and the velocity,the zero mean processes ξj (t) are stationary excitations with correlation functions Rjk (τ)=E (ξj (t)ξk (t+τ)),u denotes the external control force in the admissible set of
) represent the amplitudes of external and/or parametric random excitations,which are continuous and differentiable functions of the displacement and the velocity,the zero mean processes ξj (t) are stationary excitations with correlation functions Rjk (τ)=E (ξj (t)ξk (t+τ)),u denotes the external control force in the admissible set of 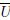 ,and the subscript "j" is a dummy index indicating a summation with the index running through its domain.
,and the subscript "j" is a dummy index indicating a summation with the index running through its domain.
By adopting the energy dissipation balance technique[19],the hysteretic damping effect can be approximated by a damping term provided that the energy dissipations in one period are equal[10].Then,the Duhem hysteretic system (4) with Eqs.(1a) and (1b) can be substituted by the non-hysteretic nonlinear random system,
in which represents the system energy,and 2ζ1 is the equivalent quasi-linear damping coefficient,which can be evaluated by the following formula: Introduce transformations to the equivalent non-hysteretic nonlinear system[20], Equation (5) can be substituted by the first-order differential equation for the system energy and phase, For the case that the damping and excitations are weak,the system energy can be approximated as a Markov diffusion process[21, 22].Performing time averaging in Eq.(9a) yields the associated Itˆo equation, where B(t) is a unit Wiener process.The drift coefficient m (H) and the diffusion coefficient σ2(H) are as follows: in which <.>t represents time averaging. 4 Optimal bounded control strategy for maximizing system reliabilityThe system energy H(t) slowly varies in the interval[0,∞).The initial state of the system is set as H (0)=H0 in the prescribed safe interval[0,Hc).Once the system energy H(t) is not in[0,Hc),the system fails.The reliability describes the probability of system in[0,Hc) within the specified time interval,which is the crucial concept.In the following part of the paper,the procedures of establishing control strategy to enhance the system reliability of Duhem hysteretic systems are illustrated.
Select the reliability function as the performance index of the controlled system (10),
Give the function V(H,t),a value function,as follows: Based on Bellman'programming principle[11],the dynamical programming equation with respect to V(H,t) derived from the system (10) can be written as The solution conditions of Eq. (15) are Equations (15) and (18) constitute the definite problem to determine the control strategy for maximizing system reliability. The control constraint is of the following form: Clearly,the term u (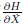 )(
)(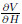 ) in Eq.(15) is maximal when|u|=b,and each term u (
) in Eq.(15) is maximal when|u|=b,and each term u (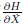 )(
)(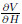 ) is positive.Thus,the optimal control forces can be written as
where sgn (·) is the sign function.It can be seen that the reliability function increases as the system energy H decreases[17],i.e.,
) is positive.Thus,the optimal control forces can be written as
where sgn (·) is the sign function.It can be seen that the reliability function increases as the system energy H decreases[17],i.e.,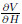 < 0.Thus,Eq.(20) can be rewritten as
5 Backward Kolmogorov equation
< 0.Thus,Eq.(20) can be rewritten as
5 Backward Kolmogorov equation
By inserting Eq.(21) into Eq.(10) for replacing u and averaging the term u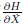 ,the following stochastic equation is derived:
,the following stochastic equation is derived:
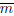 (H0) and σ2(H0) are obtained from Eqs.(23a) and (23b) with H replaced by H0.The initial condition of Eq.(24) is
and the associated boundary conditions are
The one-dimensional initial-boundary value problem,Eqs. (24)-(26),can be calculated numerically.
The conditional probability density of the first-passage time is the gradient of the conditional reliability function,
Then,the mean of first-passage time (tMFP) can be obtained from p(T|H0) through Eq. (27),
The relative increase of tMFP,which reflects the capacity and effects of the optimal bounded controller to enlarge tMFP,is used to evaluate the control effectiveness and defined as
where the subscripts "u" and "c" are the uncontrolled and controlled situation,respectively,and|·|represents the absolute value of "·" .tMFP of the controlled system is obtained from Eq.(28),and that of the uncontrolled system is obtained from Eqs.(22)-(28) by omitting the control term,i.e.,replacing
(H0) and σ2(H0) are obtained from Eqs.(23a) and (23b) with H replaced by H0.The initial condition of Eq.(24) is
and the associated boundary conditions are
The one-dimensional initial-boundary value problem,Eqs. (24)-(26),can be calculated numerically.
The conditional probability density of the first-passage time is the gradient of the conditional reliability function,
Then,the mean of first-passage time (tMFP) can be obtained from p(T|H0) through Eq. (27),
The relative increase of tMFP,which reflects the capacity and effects of the optimal bounded controller to enlarge tMFP,is used to evaluate the control effectiveness and defined as
where the subscripts "u" and "c" are the uncontrolled and controlled situation,respectively,and|·|represents the absolute value of "·" .tMFP of the controlled system is obtained from Eq.(28),and that of the uncontrolled system is obtained from Eqs.(22)-(28) by omitting the control term,i.e.,replacing 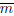 (H0) in Eq.(23a) by m (H0) in Eq.(11).Obviously,a higher K indicates a better control strategy.
6 Example
(H0) in Eq.(23a) by m (H0) in Eq.(11).Obviously,a higher K indicates a better control strategy.
6 Example
Consider a tall building under random excitations.The hysteretic behavior plays an important role in the structural response and cannot be ignored.It is reasonable that the building is idealized as a hysteresis column supporting[23](as shown in Fig. 2).The transverse motion of the column is the following partial differential equation: ,where m denotes the mass of column per unit length,and c is the damping coefficient.Assume that W is dominated by the first vibration mode,W(y,t)=X(t) sin(
,where m denotes the mass of column per unit length,and c is the damping coefficient.Assume that W is dominated by the first vibration mode,W(y,t)=X(t) sin( ).Then,the non-dimensional equation of the controlled column-mass model is
).Then,the non-dimensional equation of the controlled column-mass model is
 |
| Fig. 2 Tall building subjected to random excitations and control |
The system energy H is the averaged Itô equation for the controlled system in the form of Eq.(22),and the associated drift and associated diffusion coefficients of the system (30) are,respectively[24],
The conditional reliability function R (t|H0) for the system (30) is determined by Eq.(24).The corresponding initial and boundary conditions are given in Eqs.(25) and (26),in which 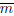 (H0) and σ2(H0) coincide with Eqs.(36a) and (36b) except that H is replaced by H0.The relations of the function p (T|H0) and the function R (t|H0) have been shown in Eq.(27).The function R (t|H0),the function p (T|H0),the mean time of the first-passage tMFP (T|H0),and the control effectiveness K can be evaluated by the numerical technique.
(H0) and σ2(H0) coincide with Eqs.(36a) and (36b) except that H is replaced by H0.The relations of the function p (T|H0) and the function R (t|H0) have been shown in Eq.(27).The function R (t|H0),the function p (T|H0),the mean time of the first-passage tMFP (T|H0),and the control effectiveness K can be evaluated by the numerical technique.
Suppose that the boundary of system first-passage failure is Hc=0.5,and the other parameter values are γ=2.0,β=0.3,D1=0.2,D2=0.05,k1=2.0,k3=0.05,and H0=0.Equation (24) combined with its initial-boundary conditions in Eqs.(25) and (26) can be solved.The numerical results for the R (t|H0) function,the p (T|H0) function,and the function tMFP (T|H0) are shown in Fig 3-Fig 5,respectively.It can be seen from Fig 3-Fig 5 that the control strategy greatly enhances the system reliability and tMFP of the Duhem system.When the magnitude b of the control force decreases,the reliability decreases more quickly,and tMFP decreases.The effectiveness of the optimal bounded control strategy is shown in Fig. 6.The control efficacy decreases as the control magnitude b increases.
 |
| Fig. 3 Conditional reliability functions R (t|H0) of uncontrolled and optimally-controlled systems (30) |
 |
| Fig. 4 Conditional probability densities p (T|H0) of first-passage time of uncontrolled and optimally-controlled systems (30) |
 |
| Fig. 5 Mean of first-passage time tMFP (T|H0) of optimally-controlled system (30) with different values of control magnitude b |
 |
| Fig. 6 Control effectiveness K versus control magnitude b |
In this study,the optimal bounded control of Duhem hysteretic systems for maximizing the reliability is developed.The controlled hysteretic system is substituted by a controlled nonlinear system without hysteresis,and the controlled system energy's Itˆo equation is deduced.The optimal bounded control for enlarging system reliability is obtained by the dynamical programming principle.Then,the conditional reliability function governed by the Kolmogorov equation is obtained.The results associated with the system reliability of uncontrolled and controlled systems obtained from the present procedure and the results from the Monte-Carlo simulation are in good agreement.Also,it can be concluded that the reliability of Duhem hysteretic systems will be really enhanced by the optimal bounded control.Finally,we note that the proposed technique cannot be adopted to derive the optimal unbounded control strategy,since the unbounded control strategy makes the dynamical programming equation unsolvable.
| [1] | Simiu, E. and Scanlan, R. H.Wind Effects on Structures:An Introduction to Wind Engineering, John Wiley and Sons, New York (1986) |
| [2] | Anagnos, T. and Kiremidjian, A. S. A review of earthquake occurrence models for seismic hazard analysis. Probabilistic Engineering Mechanics, 3(1), 3-11(1988) |
| [3] | Bouc, R. Forced vibration of mechanical systems with hysteresis. Proceedings of the 4th Conference on Nonlinear Oscillation, Prague, Czechoslovakia (1967) |
| [4] | Dahl, P. R. Solid friction damping of mechanical vibrations. AIAA Journal, 14(12), 1675-1682(1976) |
| [5] | Wen, Y. K. Method for random vibration of hysteretic systems. ASCE Journal of the Engineering Mechanics Division, 102(2), 249-263(1976) |
| [6] | Yar, M. and Hammond, J. K. Modeling and response of bilinear hysteretic systems. ASCE Journal of Engineering Mechanics Division, 113(7), 1000-1013(1987) |
| [7] | Kougioumtzoglou, I. A. and Spanos, P. D. An approximate approach for nonlinear system response determination under evolutionary stochastic excitation. Current Science, 97(8), 1203-1211(2009) |
| [8] | Mayergoyz, I. D. Mathematical Models of Hysteresis, Springer-Verlag, New York (1991) |
| [9] | Visintin, A. Differential Models of Hysteresis, Springer-Verlag, Berlin (1994) |
| [10] | Ying, Z. G., Zhu, W. Q., Ni, Y. Q., and Ko, J. M. Stochastic averaging of Duhem hysteretic systems. Journal of Sound and Vibration, 254(1), 91-104(2002) |
| [11] | Bellman, R. Dynamic programming and stochastic control processes. Information and Control, 1(3), 228-239(1958) |
| [12] | Fleming, W. H. and Soner, H. M. Controlled Markov Process and Viscosity Solutions, Springer, New York (1992) |
| [13] | Yong, J. Y. and Zhou, X. Y. Stochastic Controls, Hamiltonian Systems and HJB Equations, Springer, New York (1999) |
| [14] | Zhu, W. Q., Ying, Z. G., and Soong, T. T. An optimal nonlinear feedback control strategy for randomly excited structural systems. Nonlinear Dynamics, 24(1), 31-51(2001) |
| [15] | Zhu, W. Q., Huang, Z. L., and Yang, Y. Q. Stochastic averaging of quasi-integrable Hamiltonian systems. ASME Journal of Applied Mechanics, 64(4), 975-984(1997) |
| [16] | Zhu, W. Q. Nonlinear stochastic dynamics and control in Hamiltonian formulation. Applied Mechanics Reviews, 59, 230-248(2006) |
| [17] | Zhu, W. Q., Huang, Z. L., and Deng, M. L. Feedback minimization of first-passage failure of quasi non-integrable Hamiltonian systems. International Journal of Non-Linear Mechanics, 37(6), 1057-1071(2002) |
| [18] | Li, X. P., Huan, R. H., and Wei, D. M. Feedback minimization of the first-passage failure of a hysteretic system under random excitations. Probabilistic Engineering Mechanics, 25(2), 245-248(2010) |
| [19] | Lin, Y. K. and Cai, G. Q. Probabilistic Structural Dynamics:Advanced Theory and Application, McGraw-Hill, New York (1995) |
| [20] | Lin, Y. K. and Cai, G. Q. Some thoughts on averaging techniques in stochastic dynamics. Probabilistic Engineering Mechanics, 15(1), 7-14(2000) |
| [21] | Xu, Y., Xu, W., Mahmoud, G. M., and Lei, Y. M. Beam-beam interaction models under narrowband random excitation. Physica A, 346, 372-386(2005) |
| [22] | Xu, Y., Zhang, H. Q., and Xu, W. On stochastic complex beam-beam interaction models with Gaussian colored noise. Physica A, 384, 259-272(2007) |
| [23] | Tsiatas, G. and Sadid, H. Earthquake response of hysteretic mass-column using non-Gaussian closure. Soil Dynamics and Earthquake Engineering, 10(5), 256-263(1991) |
| [24] | Jin, X. L., Huang, Z. L., and Leung, Y. T. Nonstationary probability densities of system response of strongly nonlinear single-degree-of-freedom system subject to modulated white noise excitation. Applied Mathematics and Mechanics (English Edition), 32(11), 1389-1398(2011) DOI 10.1007/s10483-011-1509-7 |
 2015, Vol. 36
2015, Vol. 36



































